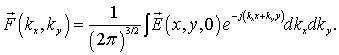УДК 001.891.573

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИФРАКЦИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ НА РАДИОПОГЛОЩАЮЩЕМ МАТЕРИАЛЕ В КОМПАКТНОМ ПОЛИГОНЕ

 

А. В. Никитенко ^1,2, А. С. Зубов ² , А. Н. Боголюбов ¹

¹ МГУ имени М.В. Ломоносова, физический факультет

² ИТПЭ РАН

 

Статья поступила в редакцию 9 ноября 2015 г.

 

Аннотация. В работе выполнено математическое моделирование компактного полигона. Рассматривается ряд факторов, искажающих поле в рабочей зоне, связанных с неидеальностью радиопоглощающего материала. Предложен строгий метод расчета задачи дифракции поля коллиматора на РПМ, расположенном на стенках безэховой камеры. Проведено компьютерное моделирование поля в рабочей зоне компактного полигона.

Ключевые слова: метод связанных волн, радиопоглощающий материал, безэховая камера, компактный полигон.

Abstract. Numerical model for electro-magnetic field in the compact range is developed. The model takes into account several factors that affect quasi-plane field in the quiet zone, factors produced by imperfection of radio-absorbing material in particular. A rigorous method for solving diffraction of the collimator’s field on RAM problem is presented. Results of computer simulations of the field in the compact range are presented.

Key words: 3D RCWA, radio-absorbing material, unechoic chamber, compact range.

 

Введение

Проведение измерений электромагнитных характеристик антенн, таких как коэффициент усиления, диаграмма направленности, а также  измерения эффективной площади рассеяния различных объектов проводятся на специальных измерительных комплексах, называемых компактными полигонами. Основными компонентами компактного полигона являются безэховая камера и коллиматор. Стенки безэховой камеры покрыты радиопоглощающим материалом (РПМ), внутри камеры расположен коллиматор, состоящий из облучателя и зеркала. Коллиматор создает квазиплоское поле в так называемой рабочей зоне – объеме пространства внутри камеры, в пределах которого неравномерность амплитуды и фазы поля не превышает заданного значения. Стенки, покрытые РПМ, обеспечивают минимальное отражение. Таким образом в компактном полигоне моделируются условия открытого пространства. Исторический обзор и более подробную информацию по безэховым камерам, компактным полигонам и РПМ можно найти в работах [1 - 3].

Последнее время  требования к точности электродинамических измерений возрастают, что предъявляет все более высокие требования к точности измерительных комплексов. Помимо этого, компактный полигон – это еще и очень дорогостоящий комплекс. Его стоимость существенно зависит от размеров камеры, например, стоимость одного только РПМ пропорциональна квадрату линейного размера камеры. Это порождает естественную потребность в оценке параметров и характеристик полигона перед его непосредственным строительством, поэтому особую актуальность имеют как можно более точные численные модели, позволяющие на компьютере рассчитать характеристики будущего полигона, оптимизировать их, варьируя различные параметры, такие как размер, расположение РПМ, свойства РПМ и другие.

Существует две основные группы факторов, влияющих на неравномерность поля в рабочей зоне. К первой группе относятся факторы, связанные с неидеальностью зеркала и облучателя коллиматора, ко второй – связанные с неидеальностью радиопоглощающего материала. В данной работе рассматриваются эффекты, искажающие поле в рабочей зоне, связанные с отражением поля, создаваемого коллиматором, от РПМ.

Существует ряд работ, посвященных математическому моделированию компактных полигонов. Все эти публикации также можно условно разделить на два типа. К первому относятся работы, в которых большое внимание уделено моделированию облучателя и зеркала коллиматора, а влияние радиопоглощающего материала не учитывается. Ко второму типу можно отнести работы, в которых исследуется влияние неидеальности РПМ на поле в рабочей зоне, однако в этих работах в качестве устройства, создающего поле вместо зеркала и облучателя используются более простые модели, например изотропная антенна, точечный излучатель с заданной диаграммой направленности.  Кроме того, исследование ведется чаще всего нестрогими, оценочными методами. Например, радиопоглощающий материал заменяется на однородную эффективную среду, для вычисления электромагнитных характеристик которой предлагаются различные способы [4 – 6].

Наиболее распространенными на сегодняшний день являются РПМ пирамидальной и клиновидной формы [7]. Поскольку, как правило, рабочая длина волны полигона сравнима с характерным размером геометрической фигуры, форму которой имеет радиопоглощающий материал, то может иметь место отражение под углами, отличными от угла падения, т.е. могут образовываться дифракционные лепестки. Моделирование типичных РПМ показало, что при нормальном падении дифракционные лепестки могут значительно превышать уровень зеркального отражения [8 – 11]. Поэтому в данной работе учитывается полное отражение, включая дифракционные лепестки, при расчете отражения от задней стенки камеры. Боковые стенки  облучаются под скользящими углами, поэтому зеркальное отражение играет ключевую роль в этих случаях. В работе предложен способ расчета отражения от боковых стенок.

Постановка задачи

В данной работе моделируются искажения квазиплоского поля коллиматора, возникающие из-за отражения поля коллиматора от радиопоглощающего материала, расположенного на 5 стенках безэховой камеры. В модели компактного полигона используются следующие приближения:

1) Для расчета поля коллиматора в свободном пространстве используется метод физической оптики, непосредственно расчет проведен с помощью пакета программ FEKO.

2) Особенности отражения от стыков стенок камеры, а также от углов не учитываются, отражение от каждой стенки рассчитывается отдельно, независимо друг от друга.

3) Поля, испытавшие двойное отражение от радиопоглощающего материала считаются ничтожно малыми и не учитываются в расчете поля в рабочей зоне.

4) Поскольку в случае боковых стенок поле коллиматора падает преимущественно под большими углами к нормали, величина поля основной (главной) гармоники существенно превышает величину полей высших гармоник [10, 11], поэтому в этих случаях сами поля высших гармоник не учитываются (однако коэффициент отражения для главной гармоники рассчитывается строго методом связанных волн).

5) Поле коллиматора локализовано в некоторой ограниченной области, вне которой оно равно нулю (поскольку стенки камеры металлические). Отраженное поле в свою очередь рассчитывается в той же ограниченной области, что и поле коллиматора. Поэтому задачу дифракции на конечной стенке можно заменить задачей отражения от бесконечной стенки, покрытой радиопоглощающим материалом.

Следует отметить, что при определенной конфигурации камеры также может иметь место и отражение поля облучателя от РПМ, расположенного на полу камеры. Такое отраженное поле попадает на зеркало коллиматора и отражается им в рабочую зону, что может существенно влиять на плоскостность поля в рабочей зоне. Однако этот эффект в данной работе не рассматривается.

Таким образом задача разбивается на 5 отдельных подзадач, а именно: отражение от задней стенки, от пола, от потолка и отражение от двух боковых стенок камеры. Эти задачи имеют единую постановку, однако имеют свои особенности. Опишем постановку задачи расчета отражения поля коллиматора от одной из стенок. Эта постановка характерна для всех пяти подзадач. Особенности каждой стенки будут описаны позднее.

Поле коллиматора отлично от нуля на прямоугольнике размером W x L метров. Введем декартову систему координат, как показано на рис.1. Ось Z направим вглубь радиопоглощающего материала, оси X и Y – вдоль сторон основания радиопоглощающего материала. Левый верхний угол стенки имеет координаты . Вектор электрической напряженности поля, падающего на РПМ, запишется следующим образом (для вектора магнитной напряженности выражение аналогичное):

Необходимо найти поле, возникшее в результате дифракции на РПМ.

Искомые компоненты электромагнитного поля -  и , должны удовлетворять [12]:

1) Уравнениям Максвелла:

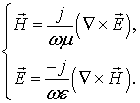
2) условию излучения на бесконечности, состоящему в том, что в рассеянном поле отсутствуют волны, приходящие из бесконечности.

3) граничным условиям, заключающимся в том, что тангенциальные составляющие векторов напряженности полного поля сохраняют непрерывность на границах раздела сред, а на поверхности металла выполняется .

4) условию пространственной интегрируемости плотности энергии рассеянного поля, состоящему в том, что для каждой конечной области V должно выполняться

 

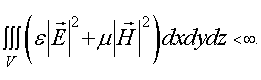
Рис. 1. К постановке задачи.

Из литературы [13 – 15] известно, что для среды с поглощением эти условия обеспечивают единственность решения исходной задачи. Для выполнения этого условия в среде без поглощения, при решении численными методами в диэлектрическую проницаемость среды  вводится небольшое поглощение.

Алгоритм расчета

Поле коллиматора, падающее на РПМ, рассчитывается методом физической оптики с помощью программы FEKO, на плоскости  в системе координат, связанной с РПМ. Введем соответствующие обозначения:

Для того, чтобы найти отраженное поле, воспользуемся методом связанных волн [10, 11, 16 – 18]. В постановке задачи для этого метода падающее поле записывается следующим образом:

,

где

 – модуль волнового вектора падающей волны, j - мнимая единица. Здесь и в дальнейших выкладках зависимость от времени  опущена. Кроме того, в условия, которым должно удовлетворять отраженное поле, добавляются т.н. периодические граничные условия, или условия Флоке.

Таким образом, чтобы свести рассматриваемую задачу рассеяния на РПМ к задаче, решенной методом связанных волн, необходимо представить падающее поле в виде суммы полей, для которых известно решение задачи отражения, и для каждого из полей - слагаемых дополнить постановку задачи следующим условием:

 

         Для падающего поля можно записать следующее выражение, представляющее собой разложение в ряд по плоским волнам:

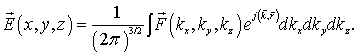                            (1)

 

Следовательно,

 

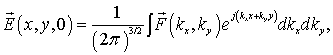
где определяется следующим образом:

                               (2)

 

Рассмотрим выражение    при фиксированных значениях . Поскольку в постановке задачи для метода связанных волн на материал падает линейно поляризованная волна, необходимо представить  в виде суммы амплитуд двух линейно поляризованных волн. В качестве двух поляризаций используем  и . Для этого введем локальную систему координат, как показано на рисунке 2. Единичный вектор  перпендикулярен плоскости падения, единичный вектор  лежит в плоскости падения.

 

 

Рис. 2. Постановка задачи с условиями Флоке.

Определим углы  и , задающие направление волнового вектора:

Имеем:

Умножив скалярно обе части равенства на , получим:

                                 (3)

Умножив на  получим выражение для :

                                                           (4)

Далее, выражение для отраженного поля имеет вид:

 

где пара индексов h₁, h₂ задают гармоники с амплитудами , и , распространяющиеся в направлении вектора , компоненты которого определяются следующим образом:

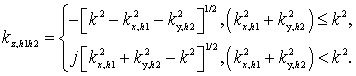
где  ,  - периоды РПМ вдоль осей X и Y.

Величины , и  рассчитываются методом связанных волн [10, 11].

Соответственно, проинтегрировав по всем отраженным волнам, получим полное отраженное поле:

                             (5)

 

Полученный алгоритм решения необходимо сформулировать в дискретном виде для реализации в виде программы и применения различных вычислительных методов и техник. Компонента вектора электрической напряженности поля, вычисляется с помощью программы FEKO в прямоугольной области размером LxW метров на однородной равномерной сетке с количеством точек по осям N_x и N_y. Увеличим сетку, добавив по каждой оси число точек до N_fur,x и N_fur,y соответственно, заполнив новые узлы сетки нулями. Размеры расширенной прямоугольной области связаны с числом точек на сетке следующим образом:

 

Величины ,  - периоды повторения падающего поля для разложения в ряд Фурье.

Введем следующую сетку:

 

 

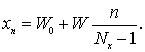
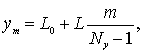
где индексы p, q пробегают значения от 0 до  и  соответственно, а индексы m, n пробегают значения от 0 до N_x-1 и N_y-1 соответственно.

Тогда интеграл Фурье (2) можно будет записать приближенно в виде суммы:

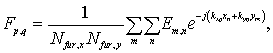
где E_m,n – значения компоненты поля в узлах сетки (здесь и далее индексы x, y, z опущены). Для повышения скорости вычисления двумерного преобразования Фурье, выделим в этой формуле т.н. быстрое преобразование Фурье (БПФ):

            

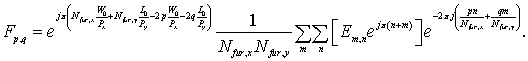
Применив описанный алгоритм ко всем трем компонентам мы получим значения амплитуд плоских волн в узлах заданной сетки, т.е. F_xp,q, F_yp,q, F_zp,q. Чтобы найти амплитуды и  p-ой  q-ой плоских волн при двух поляризациях – 0 и 90 градусов по выражениям (3) и (4), получим выражения для углов  и  :

 

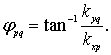
Выражение (5) на введенной сетке будет иметь следующий вид:

       (6)

 

В этой формуле так же целесообразно выделить быстрое преобразование Фурье:

 

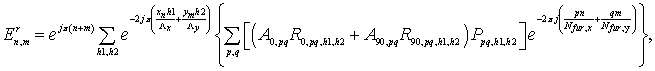
где     

 

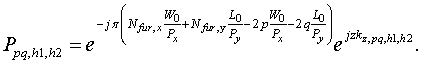
Особенности расчета различных стенок

В задаче отражения от задней стенки можно считать, что поле коллиматора падает под углами, близкими к нормали к РПМ. В этом случае больший вклад в неравномерность поля в рабочей зоне вносят высшие дифракционные порядки, в то время как зеркальное отражение достаточно мало [11]. Для каждой заданной частоты можно получить оценку сверху числа гармоник, которые необходимо учесть в расчете. Незатухающие  гармоники удовлетворяют следующему неравенству:

 

 

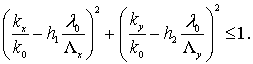
Для задней стенки можно считать, что все плоские волны - члены разложения Фурье имеют волновой вектор, близкий к нормали к плоскости стенки, т.е.  Соответственно, для индексов получаем оценку:

 

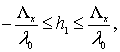
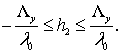
Общее число гармоник, которые необходимо учесть в расчете на данной длине волны:

 

Стоит отметить, что углы, под которыми распространяется каждая гармоника, зависят от частоты:

 

При заданной конфигурации камеры понятно, что для каждой высшей гармоники существует частота, ниже которой поле этой гармоники не попадает в рабочую зону камеры.

В случае отражения от боковых стенок можно считать, что поле коллиматора падает под углами наоборот, далекими от нормали к плоскости стенки. Расчет показывает, что в это случае величина главной гармоники существенно превышает побочные, что позволяет рассчитывать лишь зеркальное отражение. Это обстоятельство существенно упрощает выражение (6), оставляя всего одно слагаемое с номером (0,0).

Результаты расчетов

Для апробации модели была выбран компактный полигон с прямоугольной камерой. Эффективный размер камеры (то есть, размер пустого пространства камеры, ограниченного РПМ) - 6.4 x 4.8 x 15 метров. В качестве коллиматора был выбран наиболее распространенный в российских компактных полигонах микроволновый антенный коллиматор размером 4.5 x 6.03 метров. Расстояние от вершины параболоида зеркала до задней стенки – 10 метров, до центра рабочей зоны – 7 метров. Для расчетов был выбран диапазон частот от 1 до 9 ГГц. Схематично камера изображена на рисунке 3. Прямоугольные области внутри камеры соответствуют сечениям рабочей зоны камеры. Рабочая зона представляет собой цилиндр диаметром 1.8 м, длиной 3.6 м. Ось цилиндра совпадает с оптической осью зеркала коллиматора. На всех представленный графиках, где сечение рабочей зоны проходит перпендикулярно оси (как на рис. 3), центр круга рабочей зоны находится в координатах (0, 0). Все рассчитанные поля нормированы на максимальную амплитуду поля коллиматора в рабочей зоне. Алгоритм расчета реализован в виде программного комплекса, написанного на языке С++.

Рис. 3. Схематичное изображение компактного полигона.

Рис. 4. Поле коллиматора, частота 3.1 ГГц, сечение параллельно задней стенке.

 

На рисунке 4 представлено поле коллиматора, рассчитанное программой FEKO в свободном пространстве. Показано сечение, параллельное задней стенке безэховой камеры и расположенное на расстоянии 10 метров от вершины параболоида зеркала. Частота 3.1 ГГц.

Для апробации алгоритма была решена более простая задача, а именно, задача с металлическими стенками без радиопоглощающего материала. В соответствии с принципом зеркальных источников,  модуль амплитуды поля коллиматора, отраженного от металлической стенки, рассчитанного на некотором расстоянии от стенки, должен быть равен модулю амплитуды поля, рассчитанного методом физической оптики на программе FEKO, на том же расстоянии от стенки, но в другую сторону (во вне камеры). Это позволяет провести сравнение результатов расчетов полей, вычисляемых двумя различными способами. Результаты сравнения представлены на рис. 5, 6. На рисунке 5 представлены результаты расчета для задней стенки, на рисунке 6 – для боковой. В обоих случаях расстояние до стенки – 2 метра. Представлены несколько сечение в плоскости расчета. Видно достаточно хорошее совпадение результатов.

В качестве радиопоглощающего материала в рассчитываемой камере использовался широко распространенный материал пирамидальной формы, а именно Eccosorb VHP-12 фирмы-производителя Emerson & Cuming.  Период материала по обеим осям равен 0.102 м, высота материала – 0.305 м, его электродинамические характеристики и коэффициенты отражения можно найти в работе [11].

 

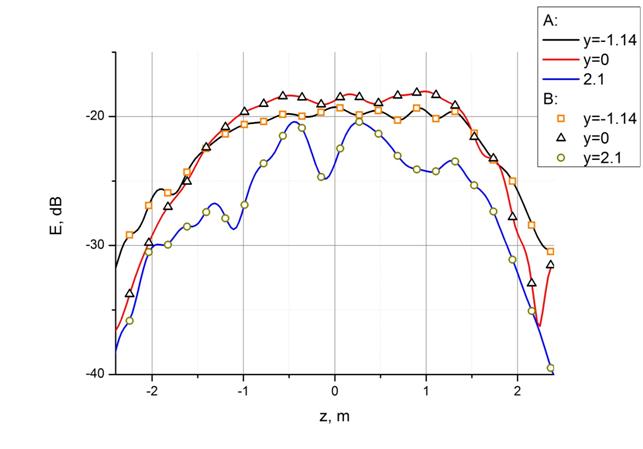
Рис. 5.Апробация алгоритма, задняя стенка.
А – расчет отражения от металла описанным алгоритмом.
B – поле зеркального источника, рассчитанное FEKO.

 

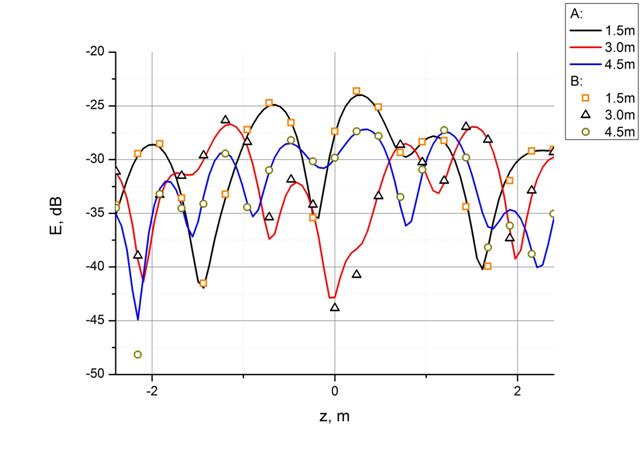
Рис. 6. Апробация алгоритма, боковая стенка.
А – расчет отражения от металла описанным алгоритмом.
B – поле зеркального источника, рассчитанное FEKO.

Рассмотрим теперь результаты расчета камеры с РПМ. На рисунках 7 – 9 представлены отраженные от задней стенки поля в сечениях камеры, параллельных задней стенке на расстоянии 0, 1 и 2 метра от нее, частота 3.1 ГГц. Для иллюстрации высших дифракционных порядков поле посчитано на квадрате большей величины, чем задняя стенка. На рисунках видно, что побочные гармоники интерферируют у самой стенки, однако затем разлетаются в разных направлениях, а зеркальное отражение настолько мало, что его не видно при данной цветовой шкале. Соответственно, при создании компактного полигона выбор корректного расстояния от задней стенки до рабочей зоны позволит избежать попадания в нее полей этих гармоник, в то время как зеркальное отражение пренебрежимо мало и не искажает поле в рабочей зоне.

Однако при большей частоте угол разлета побочных гармоник становится ближе к нормальному, и само количество гармоник так же увеличивается. Интерферируя, они могут создать существенные искажения поля в рабочей зоне. В качестве примера на рисунке 10 представлено поле, отраженное от задней стенки камеры, частота 5 ГГц, сечение параллельно задней стенке камеры, расстояние до стенки 2 метра.

 

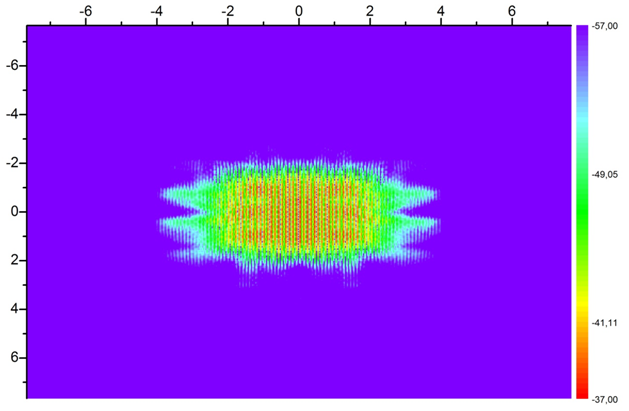
Рис. 7. Отражение от задней стенки, частота 3.1 ГГц, расстояние до задней стенки 0 м.

 

Рис. 8. Отражение от задней стенки, частота 3.1 ГГц, расстояние до задней стенки 1 м.

 

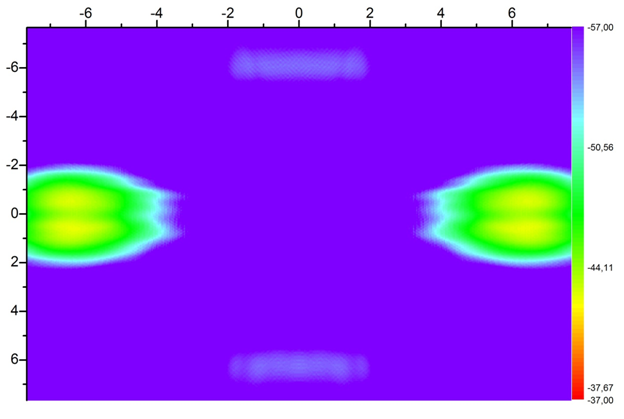
Рис. 9. Отражение от задней стенки, частота 3.1 ГГц, расстояние до задней стенки 2 м.

 

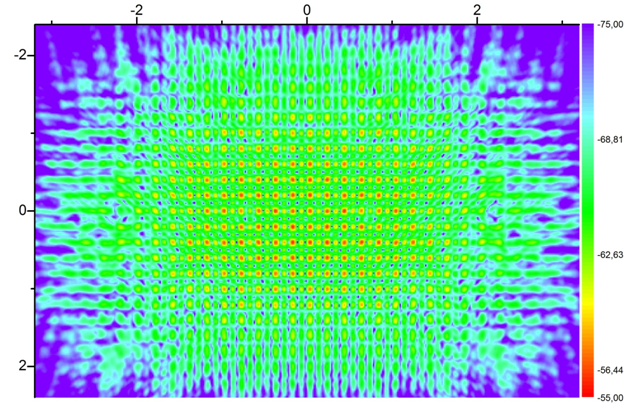
Рис.10. Отражение от задней стенки, частота 5 ГГц, расстояние до задней стенки 2 м.

На рисунке 11 представлено поле, отраженное от боковой стенки БЭК, частота 1.5 ГГц, сечение параллельно боковой стенке, расстояние от стенки – 2 метра. Как и предполагалось в модели, величина зеркального отражения от РПМ под косым углом велика. Корректное расположение рабочей зоны позволит избежать сильного влияния отражения от боковых стенок. Однако интерференция полей, отраженных от боковых стенок, пола и потолка может достигать достаточно высоких значений. На рисунке 12 представлена как раз такая ситуация – суммарное поле, отраженное от боковых стенок, пола и потолка в центральном сечении рабочей зоны, то есть в сечении, параллельном задней стенке и находящемся на расстоянии 7 метров от вершины параболоида зеркала коллиматора, в некоторых точках рабочей зоны достигает 30 дБ.

 

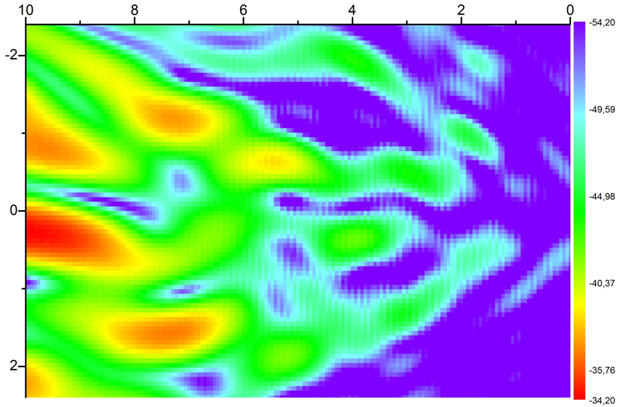
Рис. 11. Отражение от боковой стенки, частота 1.5 ГГц, Сечение параллельно боковой стенке, расстояние до боковой стенки 2 м.

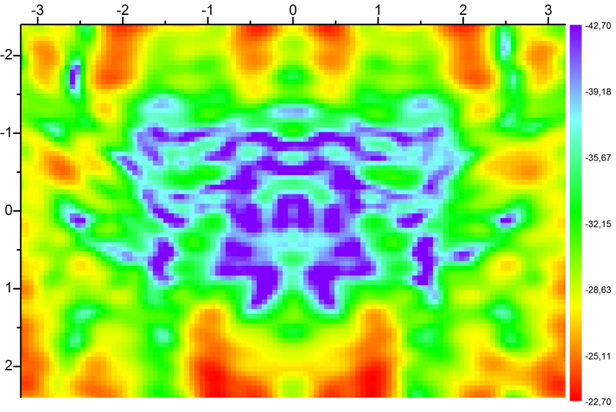
Рис. 12. Интерференция полей, отраженных от боковых стенок, потолка и пола. Частота 1.5 ГГц, центральное сечение рабочей зоны
(сечение параллельно задней стенке, расстояние до вершины параболоида зеркала коллиматора – 7 м).

 

Выводы

В работе рассматривался компактный полигон в диапазоне частот от 1 до 9 ГГц. Предложена математическая модель полигона, учитывающая рассеяние поля коллиматора на радиопоглощающем материале. Поставлена задача расчета отражения поля коллиматора от РПМ. Предложен численный алгоритм решения поставленной задачи.  Алгоритм реализован в виде программного комплекса на языке С++. С помощью предложенного алгоритма были рассчитаны основные эффекты, связанные с отражением от РПМ, вносящие вклад в неравномерность поля в рабочей зоне компактного полигона, а именно:

- отражение высших дифракционных порядков от задней стенки и их интерференция в области рабочей зоны. Продемонстрирована геометрия расположения полей этих гармоник в камере.

- зеркальное отражение от боковых стенок, поля и потолка камеры.

- интерференция полей в области рабочей зоны, отраженных от боковых стенок, пола и потолка камеры в области рабочей зоны.

Предложенный алгоритм позволяет проводить предварительные расчеты конфигурации компактного полигона,  оптимизировать геометрию безэховой камеры, расположение и выбор РПМ.

Литература

1) Hemming L.H. Electromagnetic Anechoic Chambers: A Fundamental Design and Specification Guide. Wiley-IEEE Press, July 2002, 248 p.

2) Emerson W. H. Electromagnetic wave absorbers and anechoic chambers through the years. // IEEE Transactions on Antennas and Propagation, 484–490, July 1973.

3) Балабуха Н.П., Зубов А.С., Солосин В.С. Компактные полигоны для измерения характеристик рассеяния. М.:Наука, 2007.

4) Mazanek M., Klepal K., Pechac P. Electromagnetic Field in Anechoic and EMC Chambers – Part 1 – Modelling. // Radioengineering Vol. 9, № 1, April 2000.

5) Kuester E. F., Holloway C. L. Improved low-frequency performance of pyramid-cone absorbers for application in semi-anechoic chambers. //  Proc. 1989 IEEE Int. Symp. EMC,  pp.394 -398 1989.

6) Sukov A. I., Tregubov K. V., Hayrullin I. N., Sukov S. A. Mathematical simulation of electromagnetic fields inside an anechoic chamber of rectangular shape. // Письма в ЭЧАЯ. 2008. Т. 5, №3(145). С. 303-309.

7) Severin H. Nonreflecting Absorbers for Microwave Radiation. // IRE Trans. Antennas and Propagation, vol. 4, №3, pp. 385–392, 1956.

8) Aoyagi T., Takizawa K., Kurihara H. Numerical simulations for site VSWR with consideration of diffracted wave of pyramidal electromagnetic wave absorber. //  IEEE Proc. Asia-Pacific Symp. Electromagn. Compat.,  pp.753 -756 2012.

9) Takahiro Aoyagi, Hiroshi Kurihara, Koji Takizawa, Yoshihito Hirai. Effects of Incident Directions on Reflection Coefficients of Pyramidal Electromagnetic Wave Absorber. // EMC’14/Tokyo, 14P1-A2.

10) А.В. Никитенко, А.С. Зубов, Н.Е. Шапкина. Моделирование электромагнитного рассеяния на радиопоглощающем материале методом связанных волн. //Математическое моделирование, 2014, том 26, номер 9, стр. 18-32.

11) А.В. Никитенко, А.С. Зубов, Е.В. Булычев. 3D моделирование электромагнитного рассеяния  на рпм методом связанных волн. // Журнал Радиоэлектроники (электронный журнал), номер 12, 2014 год.

http://jre.cplire.ru/jre/dec14/15/text.pdf

12) Шестопалов В.П., Кириленко А.А., Масалов С.А., Сиренко Ю.К. Дифракционные решетки. - Киев: Наук. думка, 1986. - 232 с. - (Резонансное рассеяние волн: В 2-х т.; Т.1).

13) Шестопалов В.П., Литвиненко Л.Н., Масалов С.А., Сологуб В.Г. Дифракция волн на решетках. - Харьков: Изд-во Харьк. ун-та, 1973. - 288 с.

14) Масалов С.А., Сологуб В.Г. Строгое решение задачи дифракции электромагнитных волн на одной ленточной структуре. // Журн. вычисл. математики и мат. физики, 1970, 10, №3, с. 693-715.

15) Хёнл Х., Мауэ А., Вестфаль К. Теория дифракции. – М.:Мир, 1962. – 428 с.

16) D. Maystre. M. Neviere. Electromagnetic theory of crossed gratings. // J. Optics (Paris), 1978, vol. 9, no 5, pp. 301-306.

17) E. Noponen, J. Turunen. Eigenmode method for electromagnetic synthesis of diffractive elements with three-dimensional profiles. // J. Opt. Soc. Am. A/Vol. 11, No. 9/September 1994.

18) Moraham M.G., Grann E.B., Pommet D.A., Gaylord T.K. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. // J. Opt. Soc. Am. A 12, 1068-1076 (1995).