Реализация цифровых систем СДЦ в псевдошумовых РЛС с пониженной вероятностью перехвата

УДК 621.391, 621.396

Реализация цифровых систем СДЦ в псевдошумовых РЛС с пониженной вероятностью перехвата

Ю. Н. Горбунов

Институт радиотехники и электроники им. В.А. Котельникова РАН, Фрязинский филиал

Московский государственный технический университет радиотехники, электроники и автоматики (МГТУ МИРЭА)

Статья поступила в редакцию 5 ноября 2015 г.

Аннотация. Рассматриваются возможные пути использования частотно-временного и пространственно-частотного ресурса для расширения спектра псевдошумовых РЛС с СДЦ, в том числе использующих рандомизацию приема сигналов, перестройку несущей частоты, многочастотный анализ, вобуляцию периода повторения зондирующих импульсов, использование шумовых несущих и в перспективе - полномасштабного применения шумовой сверхширокополосной радиолокации, реализующей форму тела неопределенности удовлетворяющего требованию круговой симметрии, и - обладающей повышенной скрытностью работы.

Ключевые слова: сверхширокополосная радиолокация, расширение спектра сигналов, рандомизация, заметность, скрытность, энергопотенциал.

Abstract: Possible ways of using time-frequency and spatial-frequency resource for spreading PN radar with MTI, including using randomized to receive signals, the restructuring of the carrier frequency, multi-frequency analysis, wobble period of pulse repetition, the use of noise bearing and in the future - full application noise UWB radar implementing body shape uncertainty satisfying the requirement of circular symmetry, and - having improved stealth operation, are considered.
Key words: ultra-wideband radar, expanding the range of signals, randomization, visibility, secrecy, energy potential.

Введение

Исследования на тему «современная радиолокация» идут по пути выбора вида зондирующих сигналов и совершенствования методов и средств, в общем случае цифровой стохастической пространственно-временной (ПВ) обработки эхо-сигналов в когерентных РЛС с СДЦ (класс РЛС «coherent PN radar system moving target MTI) [1,2] с конечной целью реализации её актуального требования - сниженной вероятности перехвата РЛС [3].

Как известно исторически первыми РЛС с СДЦ работали в когерентно – импульсном режиме с однозначной дальностью. Далее структура сигнала усложнялась: появились РЛС с СДЦ с неоднозначной дальностью, двухчастотные, разностно-временные, с вобуляцией частоты повторения, псевдослучайной ступенчатой частотной модуляцией несущей частоты и др.

Совершенствование РЛС с СДЦ с одной стороны шло по пути интенсивного наращивания энергопотенциала РЛС, с другой - экстенсивного освоения СВЧ диапазона длин волн и расширения ширины полосы частот DF системы передачи координатной информации, т.к. в этом случае не только снижаются требования к габаритам ФАР, но и достигается высокая скорость передачи информации (С_инф) [4,5]:

(1)

где Р_с – мощность сигнала, Р_ш – мощность шума в системе.

Для осуществления зондирований в РЛС с однозначной дальностью исторически первыми были использованы радиоимпульсы (импульсное излучение – ИИ) и длинно-импульсные сигналы (ДИ) с внутриимпульсной модуляцией сигналов на отдельных зондированиях. Такие сигналы, как правило, имели внутриимпульсное линейно - частотное (ЛЧМ) или фазо - кодо манипулированное (ФКМ) заполнение. Основная цель, достигаемая при использовании таких сигналов, – это снижение требований к ВЧ - тракту по критерию пробивного напряжения и увеличение энергии (длительности) сигнала при одновременном расширении его полосы. Ухудшение характеристик разрешения и точности по дальности компенсировалось сжатием сигналов.

Квазинепрерывные сигналы (КНИ) имели высокую частоту повторения, следовательно повышали средний уровень излучаемой мощности, но РЛС, использующие КНИ сигналы, не могли однозначно измерять дальность, как и сигналы с непрерывным излучением (НИ), обеспечивающие хорошие характеристики доплеровской селекции, разрешения и измерения скорости. Неоднозначное измерение дальности устранялось аппаратным путем и представляло собой сложную техническую задачу. Часто использовались и многочастотные сигналы и сигналы с перестройкой несущей частоты, однако это приводило к многоканальности и к росту аппаратурных затрат.

Известны шумовые РЛС, которые относятся к классу НИ РЛС [6-10].

Имея хорошие характеристики доплеровской и угловой (по аналогии) селекции, для измерения дальности и пеленга требовалось измерение положения пика корреляционной функции. Исторически первым методом создания широкополосных шумовых РЛС следует считать предложение К. Шеннона [4,5] по использованию в качестве передаваемого сигнала образцов реального шума необходимой полосы W и длительности Т. Шенноном была предложена схема построения такой системы, изображенная на рис. 1 [11].

Рис.1. Блок – схема формирования сигнала, предложенная Шенноном

Канал имеет ширину полосы W и среднюю мощность шума . Передатчик имеет ограниченную мощность Р. Используя генератор белого шума с шириной полосы W, выбираем М различных реализаций шума, длительностью Т каждая. Обозначим эти сигналы (t), (t), … (t). Каждый из этих сигналов воспроизводится и запоминается в соответствующих устройствах памяти , , … . В процессе работы системы один из сигналов (например К - й) выбирается для передачи. Сигнал, искаженный шумом в канале, записывается каждым из блоков , , … . В них из принятого сигнала вычитаются сигналы, записанные в устройствах памяти, как это делается в системах СДЦ. Полученная разность возводится в квадрат и затем интегрируется за время Т, т.е. вычисляется средний квадрат разности.

При достаточно большом времени интегрирования Т все измерительные устройства за исключением К – го дадут показания, близкие к 2Р + , что являлось мощностью разностного сигнала, Р – мощность шума приёмника. Измеритель К – го канала даст с вероятностью, близкой к 1, результат, приблизительно равный . Таким образом в К – м канале получаем наименьшее показание измерителя, т.е. в нём происходит компенсация переданного сигнала. Следовательно, при построении РЛС с СДЦ, работающих на этом принципе, будут скомпенсированы пассивные помехи - отражения от местных предметов, а сигналы движущихся целей выделены.

Стробирование шума и вычитание эхо - сигналов превращало шумовые НИ РЛС в КНИ РЛС со сжатием сигналов, но принципиально оставляло надежду реализовать простейшие устройства СДЦ. Используя терминологию узкополосных РЛС, можно предположить, что в этих РЛС сохранялась когерентность сигнала: вектор суммарного помехового эхо – сигнала от неподвижного предмета на средней частоте - был неподвижным, а вектор суммарного полезного сигнала от движущейся цели - изменялся по фазе и амплитуде и - выделялся схемой череспериодной компенсации. Несмотря на кажущуюся аналогию и простоту реализации системы СДЦ, схема, предложенная К. Шенноном, оставалась принципиально аналоговой и потому не была реализована. Этому способствовало отсутствие соответствующей элементной базы построения широкополосных трактов: генераторов хаоса и усилительных устройств. Для реализации цифровых эквивалентов отсутствовали быстродействующие АЦП и процессоры цифровой обработки сигналов.

Востребован более конструктивный подход, предполагающий путь совершенствования традиционной элементной базы дискретной твердотельной и электровакуумной электроники по пути полномасштабного внедрения в радиолокацию традиционных мощных СВЧ генераторов гармонических сигналов, но со случайными аналоговыми (вероятностными) параметрами: хаотическим периодом повторения, скачкообразным изменением частоты, фазы и др. Применение чисто шумовых аналоговых НИ сигналов для реализации РЛС большой дальности ограничивалось, т.к. требовалось обеспечение работы мощных передающих устройств в линейном (без отсечки) режиме и, соответственно, большой (70 - 90 дБ) - развязки между приёмным и передающим устройствами.

В настоящей статье предлагается стохастический подход к решению задачи, вписывающимся в направление стохастической радиолокации [1,2,13], имеющее более широкие границы применения и которое базируется на концепции внедрения в процесс обработки и формирования радиолокационных сигналов искусственной стохастичности, предполагающий наряду с естественной стохастичностью, обусловленной случайной природой входных сигналов, рандомизацию условий процесса «приём – передача». Это - введение в процессе наблюдения цели в параметры схем обработки и формирования сигналов случайных параметров, процедур и компонент. Примерами могут служить: вобуляция частоты повторения, перестройка несущей частоты, модуляция порогов квантования, использование стохастических шкал квантования и измерения, использование эталонных случайных добавок, пробных возмущений и т.п.

Первоочередными задачами являются рассмотрение возможных путей использования методами стохастической радиолокации частотно-временного и пространственно-частотного ресурса для расширения спектра псевдошумовых РЛС с СДЦ, в том числе использующих рандомизацию приема сигналов: перестройку несущей частоты, многочастотный анализ - для уменьшения боковых лепестков диаграммы обратного рассеяния (ДОР) цели, вобуляцию периода повторения зондирующих импульсов - для устранения «слепых скоростей» системы СДЦ, использование неэквидистантных шкал пеленгаторов - для устранения неоднозначности измерений и реализации принципов радиолокации высокого разрешения, псевдошумовую модуляцию квадратурных составляющих принимаемых сигналов - для уменьшения шумов квантования и увеличения подпомеховой видимости целей на фоне пассивных и активных помех. В перспективе это позволит полномасштабно использовать преимущества шумовой сверхширокополосной радиолокации [10], в которой реализуется форма тела неопределенности РЛС, удовлетворяющей требованию круговой симметрии, и - обладающей повышенной скрытностью работы, но синтезированной в цифровом виде.

Стохастическая радиолокация

Традиционную радиолокацию обычно не называют стохастической, но этот термин очень распространен (см., например, Сосулин Ю. Г. Теория обнаружения и оценивания стохастических сигналов. - М.: Советское радио, 1978. – 320 с.). В этой работе рассматривается применение статистической теории к зашумленным и искаженным случайными помехами детерминированным сигналам. Реже применяются стохастические критерии (правила) для решения задач обнаружения и оценки параметров стохастических сигналов.

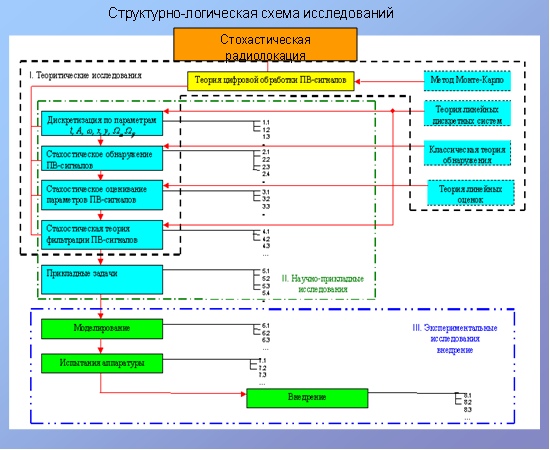
Обобщение работ по анализируемому направлению позволяет представить структурную схему теории стохастической радиолокации, которая приведена на Рис. 2.

Теория цифровой стохастической обработки ПВ сигналов (теория стохастической радиолокации) сегодня до конца не разработана. Достигнутый уровень – это сформировавшаяся совокупность идей, способов, устройств, алгоритмов. Идейной основой теории стал метод Монте-Карло, в дальнейшем применявшийся в основном в вычислительной математике и моделировании. Адаптация этого метода применялась ранее [1,2,13].

Рис. 2. Структурно-логический базис стохастической радиолокации

Применительно к решению задач, выходящих за рамки теории ПВ обработки, можно также упомянуть следующие имена: В.Г. Гайсов, Кан, Шапиро, А.К.Микельсон, Р.Ф. Немировский, И.Я. Билинский, Э.И. Вологдин, Г.П. Вихров, В.С. Гладкий, В.Г. Стругач, Ю.Г. Полляк, О.Н. Граничин, Б.Т. Полляк, В.И. Фомин и ряд других, известных в кругу специалистов, применяющих рандомизацию для решения различных задач, включая задачи вероятностного моделирования.

Стохастические радары с цифровой ПВ обработкой обеспечивают подавление помех и цифровое когерентное накопление сигналов с формированием провалов «нулей» как по оси не только обычных, так и оси пространственных частот (угловых направлений) [12]:

, (2)

, (3)

где l- средняя длина волны, q-пеленг – направление прихода электромагнитного излучения по отношению к оси антенны, a-азимут, b-угол места цели.

Первой важной структурной компонентой исторически сформировавшегося структурно-логического базиса стохастической радиолокации является компонента дискретизации и квантования. Это:

- квантование во времени , обусловленное периодической структурой когерентно-импульсного сигнала («медленное время» по пачке импульсов) и отдельных реализаций эхо-сигналов («быстрое время» по одному периоду зондирований);

- квантование пространства по осям и электромагнитного (ЭМ) поля в апертуре ФАР РЛС;

- квантование по уровню амплитуды сигналов и фазы сигнала в каналах ПВ фильтрации (в квадратурных каналах);

- квантование координат и параметров движения цели, каковыми могут быть дальность , пеленг , скорость V (доплеровское смещение частоты );

- квантование обычных и пространственных и частот в апертуре ФАР РЛС, что в свою очередь связано с квантованием угловых направлений по азимуту и углу места [15];

- квантование распределений, поскольку входной ПВ сигнал (поле) в процессе его наблюдения представляет собой случайный процесс, развивающийся во времени.

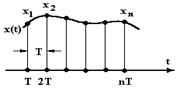
Квантование по времени превращает непрерывные функции (сигнала) x(t), в решетчатые функции x(nT), n = 0, 1, 2,… , где T – интервал временного квантования по каждой из квадратурных составляющих сигнала с выхода фазовых детекторов по видео для системы СДЦ (см. Рис. 3).

а)

б)

Рис. 3. Квантование по времени: а – получение решетчатых функций;

б – эхо-сигналы в N зондированиях с периодом повторения Т

При обычной обработке дискретизатор во времени - это ключ, замыкаемый через промежутки времени T, далее преобразователь уровня в двоичный код - аналого-цифровой преобразователь АЦП. Теорема отчетов определяет условия, при которых такое квантование возможно и потери информации отсутствуют. При стохастической обработке размеры ПВ выборок тесно связаны с самой процедурой дискретизации и квантования и порядком ЦФ, определяющим число степеней свободы, и, поэтому, показана связь этого блока с блоками «Теорема отсчётов» и «Теория линейных дискретных систем».

Блок стохастического обнаружения ПВ сигналов предполагает рандомизацию обнаружения цели радаром, поскольку обеспечение инвариантности (независимости от распределения) в условиях нестационарных шумов и помех требует использования коротких «обучающих» выборок, непараметрической и ранговой статистики.

Стохастическое оценивание (измерение) параметров ПВ сигналов, которое в дальнейшем мы назвали «рандометрией», осуществляется отдельным блоком на схеме Рис. 2, хотя это выделение отражает особенности решения функциональных задач и не претендует на законченность их решения вне связей с соседними блоками.

Блок стохастической фильтрации ПВ сигналов поставлен четвёртым по ходу обработки ПВ сигналов, однако очевидно, что эта фильтрация может осуществляться как по высокой, так и по низкой частоте, т.е. после гетеродинирования.

При описании внутренних и внешних связей обратим внимание на внутреннее взаимодействие блоков «квантования», «обнаружения», «оценивания» и «фильтрации» в чисто описательном плане. Эта совокупность блоков имеет две внешние связи с теорией линейных дискретных систем, т.е. предполагает использование принципа суперпозиции сигнальных воздействий и их откликов по аналогии с линейными аналоговыми системами. Однако операции дискретизации и квантования сугубо нелинейные, тем более, если эти операции являются достаточно «грубыми». Метод стохастической линеаризации, устраняет эти противоречия, т. к. в нём реализуется операция аппроксимирующего усреднения.

Бинарными свойствами обладает операция «жесткого широкополосного ограничения – фильтрации», примененная в 70-х гг. Ю.Б. Черняком в радарах. Им доказаны линейные свойства такой обработки, что не является парадоксом, а скорее подтверждает существование некоторой закономерности, которую мы сегодня оформлена в новую теорию. Статистическая теория обнаружения в классической формулировке при проверке гипотез оперирует вероятностями, которые являются первыми моментами бинарной - знаковой («грубой») статистики входного сигнала.

Оператор математического для квадратов напряжений с целью сохранения преимуществ, присущих аналоговым системам, допускает применение случайных порогов и уравнивает ситуацию по достижимым вероятностям правильного обнаружения P_D и ложной тревоги P_F, сниженным уровням боковых лепестков для «стохастического» и «нестохастического» случаев. Это подобие использовалось в теории квантования распределений Шеппарда (поправки Шеппарда учитывают шум квантования распределений для стационарных процессов).

Сказанное относится к блокам «стохастического оценивания» и имеющего с ним внешнюю связь – теорию оценок Фишера (теорию линейных оценок, которая оперирует моментами более высоких порядков, включая смешанные моменты и корреляцию. Однако, и в этом случае принцип подобия на основе равенства моментов непрерывных аналоговых процессов и их цифровых эквивалентов (в стохастическом случае) оставляет простор для поиска большого многообразия оригинальных инженерных решений по построению устройств оценивания, по существу являющихся цифровыми, но обладающими «аналоговыми» (Ю.Г.) свойствами.

Наконец, блок «стохастической фильтрации», который приобрел характеристику «стохастический» в основном за счет стохастического АЦП, однако в случае использования случайных весовых коэффициентов как в прямых, так и в обратных связях он действительно становится таковым [16]. Получение структур стохастических цифровых фильтров принципиально было невозможным в ограниченных рамках классической теории линейных дискретных систем.

Термины «стохастичность», «линеаризация», «обеление», «рандомизация» – почти синонимы, имеющие разные оттенки толкования в зависимости от решаемой задачи.

Рандомизация

Виды естественного приращения стохастичности, связанного с наличием собственных тепловых шумов приемника, проявляются на выходе амплитудного (АД) и фазового детектора (ФД) одного элемента ФАР в виде распределений Релея и Гаусса (нормального) соответственно (см. Рис.4). Статистику наблюдений входного сигнала в условиях рандомизации приема назовем «грубой» (ГС), если она обладает бинарными свойствами, т.е. для единичной ПВ выборки имеет «грубые» µ = для АД или µ = для ФД.

В первом случае µ = - есть результат пороговой обработки, т.е. сравнения напряжения u(t) c порогом бинарного квантования, а во втором случае для каждой квадратурной компоненты входного сигнала u(t) - имеем непараметрическую робастную (бинарно-знаковую) µ = . Непараметрическая статистика µ = также может быть образована при сравнении двух отсчетов напряжения u(t), взятых в различные моменты времени на выходе АД. Такую статистику в зарубежной литературе называют статистикой Манна -Уитни.

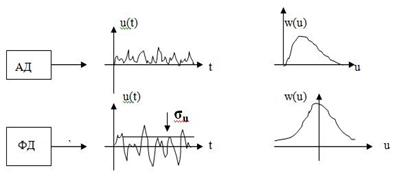
Рис.4 Сигналы на выходе детекторов

Применительно к задачам СДЦ на Рис. 5 представлена схема формирования квадратурных составляющих сигнала, в которой на квадратурные входы подмешаны шумовые хаотические напряжения x с нулевым средним.

Рис

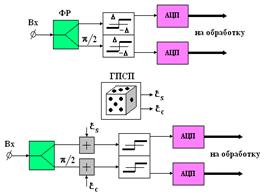
Рис. 5. Схема формирования грубых отсчетов с рандомизацией бинарно - знаковой статистики

Искусственный фазовый джиттер (дрожжание) рандомизирует отсчеты фазы пространственных частот и, таким образом к стохастической интерполяции отсчётов пеленга, который считается постоянным в пределах анализируемой ПВ выборки. Это является эквивалентным стохастической модуляции положения фазового центра на приём – передачу.

Таким образом, применяется технический приём, в котором применяется рандомизация обработки сигналов путём искусственного внесения элементов стохастичности при сохранении когерентности исходного сигнала.

При прочих равных условиях параметры системы СДЦ с цифровой ПВ обработкой: разрядность АЦП и данных, частоты дискретизации, размеры окон пространственных и временных выборок должны быть выбраны по возможности минимальными, однако это становится несовместимым с требованием обеспечения высокой эффективности системы обработки, т. к. растут шумы квантования и боковые лепестки (эффект Гиббса), возникают эффекты стробоскопического характера – «слепые фазы», «слепые направления», «слепые скорости», провалы в ДОР цели и др., которые устраняются рандомизацией.

Шумовые РЛС относятся к классу РЛС с КНИ сигналами, но для построения многоканальных по дальности, скорости, угловым координатам соответствующих подсистем, равномерного поступления координатно – доплеровской информации такие РЛС по существу превращаются в псевдошумовые КНИ РЛС, т. к. без квантования времени и пространства реализовать эффективную обработку без привлечения различного рода «дискретизаций», «аналого-цифрового преобразования», «уплотнений», «прореживаний», «наложением окон», т.е. ЦО практически реализовать невозможно.

Разрешение и широкополосность

Таким образом стохастическая радиолокация – это направление (вектор) развития современной радиолокации в сторону шумовой радиолокации, основанной на рандомизации обработки и формирования сигналов в радиолокации [1,2] и связи [13] с целью расширения спектра обычных и пространственных частот.

Широкополосность системы определяется не абсолютной величиной ширины используемой полосы частот, а соотношением спектра сообшения (он определяется скоростью поступления информации (в РЛС координатной и доплеровской), которую необходимо передать потребителю) и спектра сигнала, определяемого избранным видом модуляции.

Пусть DF – ширина спектра сообщения, W – ширина спектра сигнала и Т – длительность сигнала. Произведение В = WT обычно называют базой сигнала. Для узкополосных систем приближенно выполняются соотношения DF = W, а В = WT = 1. Для широкополосных систем обычно W ≫ DF и В ≫ 1.

Отношение = W/DF , называемый коэффициентом расширения полосы показывает, во сколько раз мы расширяем спектр сообщения. Расширяя полосу частот с DF до W, мы могли бы увеличить скорость передачи информации, укоротив передаваемые сигналы с величины Т 1/DF до 1/W, причём . Но тогда мы снова получили бы узкополосную систему с базой = W. Не увеличивая скорость передачи информации, мы тем самым вводим в передаваемый сигнал некоторую избыточность, величина которой определяется коэффициентом расширения спектра = W/DF. Именно наличием этой избыточности определяются полезные свойства широкополосных систем: возможность преодоления явления многолучёвости, устойчивость к помехам и возможность эффективного использования спектра при перегруженном диапазоне частот и организации многоканальной обработки сигналов по доплеровской частоте и угловым координатам, устранения нежелательных эффектов ЦО.

В радиолокации, кроме этого, - возможность повышения разрешающей способности и точности измерения координат и параметров движения. Из теории потенциальной помехоустойчивости В.А. Котельникова известно, что характеристики обнаружения и точности зависят от величины Q = 2Е/, равной отношению удвоенной энергии сигнала к спектральной плотности мощности (СПМ) шума и этой величине равны максимальное значение и дисперсия шумовой функции сигнальной функции на выходе согласованного фильтра ( или коррелятора).

Величина Q = 2Е/ входит во многие соотношения теории потенциальной помехоустойчивости и играет фундаментальную роль, для СШП сигналов её можно представить в следующем виде:

Q = 2Е/ = 2, (4)

где = – отношение средней мощности сигнала = Е/Т к мощности шума = W на входе приёмника, В = WT – база сигнала.

База В представляет собой коэффициент сжатия, в результате чего в В раз повышается разрешающая способность системы, а вводимая в сигнал избыточность, позволяет достичь некоторые вышеуказанные преимущества.

Проблема реализации РЛС со сниженным уровнем вероятности вскрытия (перехвата)

Для оценки заметности сигнала в задачах электромагнитной совместимости (ЭМС) и РТР часто используют показатель заметности во временной области , равный отношению максимальной мгновенной пиковой мощности сигнала к его средней по времени мощности :

= / (5)

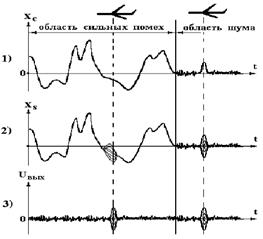
Этот показатель для непрерывных СШП сигналов при его анализе Наблюдателем во временной области (в «режиме осциллографа») может быть близок к единице. В случае, если Наблюдатель анализирует сигнал в частотной области (в «режиме спектроанализатора»), то по аналогии с (5) можно использовать показатель заметности в частотной области, равный отношению максимальной спектральной мощности сигнала к его средней по спектру мощности :

/ . (6)

Этот показатель может быть намного больше единицы. При использовании в качестве несущих колебаний стохастических СШП сигналов x(t), представляющих собой стационарный случайный процесс с нулевым средним и корреляционной функцией R () = M [x(t)] (M – оператор математического ожидания) для значения времени корреляции , соотношения между показателями заметности во временной и частотных областях могут поменяться. Известное равенство Парсеваля, допускающее множественность представлений сигнала во временной и частотных областях при сохранении его энергии Е = const, с учетом обобщений, связанных с введением понятия эргодического процесса, сделанных Винером и Хинчиным и полученной ими взаимосвязи между СПМ и корреляционной функцией стационарного случайного процесса в виде пары преобразований Фурье позволяет это сделать.

Для СШП сигналов:

R (0) / , (7)

/ , (8)

где R (0) – значение корреляционной функции R () для времени корреляции = 0, - средняя по времени мощность, максимальная спектральная плотность мощности сигнала, - средняя спектральная плотность мощности сигнала.

Очевидно, что предлагаемые для реализации псевдошумовые РЛС должны иметь тело неопределённости, удовлетворяющей форме круговой симметрии с пиком в точке 0 и окружностью радиусом = 1/ в основании и базой В = NМL, где N – размер временной выборки, ML – размер пространственной выборки в апертуре ФАР (М – по азимуту, L – по углу места). Ниже проведём сравнение сигналов по критерию широкополосности на частотно – временной диаграмме, осуществляемое при одинаковом среднем отношении сигнала , равном отношению = Е/Т к мощности шума = W (W – полоса сигнала) на входе приёмника определяется базой В и делает использование СШП сигналов по отношению к «составным» (имеющим различные виды модуляции: стробирования, дискретизации, наложением окон и другими решетчатыми и полосно – пропускающими структурами и т.п.) более эффективным.

При энергетическом вскрытии излучения передатчика средствами радиотехнической разведки (РТР) параметр Q РЛС также имеет важное значение, но корреляционную (согласованную обработку) система РТР осуществлять не может.

Как известно из [14], тело неопределённости зондирующего сигнала должно быть остроконечного типа («игольчатым», «кнопочным», «с симметрией тела вращения», «в форме объёмной - функции»- Ю.Г.), при этом соответствующий ему сигнал должен быть «продолжительным и широкополосным», и ему характерна и «существенна хаотичность в законе модуляции» [14]. Учитывая известную аналогию между «частотно – временным» и «пространственно-частотным» подходом, естественным решаемым вопросом статьи является обобщение требования расширения спектра сигналов и требования «хаотичности в законе модуляции» как для обычных, так и для пространственных частот.

Применительно к задачам измерения пеленга [15] рандомизация бинарного квантования осуществляется с помощью схемы Рис. 5, однако вместо ансамбля выборочных значений по времени используются пространственные выборки по осям x, y апертуры ФАР: вначале происходит расширение спектра шумов квантования, а затем - усреднение ошибок измерения азимута и угла места с одновременным сжатием диаграмм направленности ФАР в соответствующих сечениях. Высота уровня фона тела неопределённости [14].

Показатель заметности для непрерывных СШП сигналов при его анализе Наблюдателем во временной области (в «режиме осциллографа») и в спектральной области (в «режиме спектроанализатора») должен быть близок к единице, что приводит к уменьшению вероятности перехвата РЛС с ростом В.

Реализация сверхразрешения: методы построения широкополосных сигналов

С некоторой натяжкой можно назвать широкополосными и другие методы, у которых произведение ТW имеет величину значительно большую единицы. Было предложено разбивать информационную посылку длительностью Т на элементы длительностью , имеющие ту же амплитуду, что и информационная посылка, но различные знаки или заполнение. Такое разбиение позволяет получить сигнал длительностью Т с полосой W 1/1. Число элементарных импульсов в информационной посылке определяется как N = T/ (Ранее В = - мы называли базой сигнала.)

Однако не всякое разбиение информационной посылки даёт сигнал, который можно использовать в широкополосной системе. Возможность разделения перекрывающихся во времени сигналов связана с наличием у корреляционной функции принимаемых сигналов единственного максимума значительной амплитуды и ширины порядка 1/W пика спектральной плотности мощности (СПМ)

Такого вида корреляционной функции обладают отрезки шума с полосой W и детерминированные сигналы, которые называют псевдошумовыми или шумоподобными [5,11]. Хаффман в своей статье [17] назвал сигналы, обладающие этим свойством, последовательностями, эквивалентными импульсу, так как после обработки в корреляционном приёмнике или согласованном фильтре они принимают вид импульса длительностью c амплитудой NS, где S – амплитуда элементарного импульса последовательности. Максимальные боковые лепестки корреляционной функции, которые определяют вредное влияние на правильный приём сигнала, имеют амплитуды порядка При достаточно большом N порядка 100 и более эти лепестки пренебрежимо малы по сравнению с главным максимумом.

При наблюдении сигнала в частотной области (спектроанализатором), имеющим разрешение , необходимо наличие аналогичного максимума у функции спектральной плотности мощности (СПМ) принимаемого сигнала - единственного максимума значительной амплитуды и ширины СПМ W/Такого вида функцией СПМ обладают отрезки спектра шума длительностью Т или другие сигналы, которые имеют аналогичные свойства. Их также можно назвать псевдошумовыми или шумоподобными сигналами.

В настоящее время известны методы образования широкополосного сигнала с помощью модуляции несущей частоты последовательностями максимального периода регистра сдвига. Так как огибающая такого сигнала постоянна, тот мощность передатчика используется максимальным образом. При приёме такой последовательности на согласованный фильтр также имеем выигрыш по мощности по сравнению с использованием одиночного импульса той же амплитуды составляет В = N = TW раз. Известно, что возможно получение широкополосных сигналов с помощью так называемого многофазного кодирования, при котором фаза несущего колебания в отличие от вышеупомянутой бинарной последовательности, может иметь большое число различных фаз от 3 до 10 и более (кроме двух 0 и ). Упомянем ещё метод получения широкополосных сигналов с помощью линейной частотной модуляции. Импульс с постоянной амплитудой, у которого частота заполняющей синусоиды изменяется линейно в полосе W в течение Т сек, удовлетворяющих условию TW 1.

Все вышеописанные методы служат для получения широкополосного сигнала, непрерывного по времени и частоте в отведённой ему частотно - временной области, определяемой полосой частот сигнала W и его длительностью Т ( см. рис.6 а ).

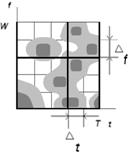
а) б) в)

Рис. 6 Частотно – временная область для системы с непрерывным (а), разрывным (б) и стохастическим (в) по времени и частоте сигналами.

При передаче одновременно нескольких импульсов на различных частотах мы получаем частотное разнесение сигнала.

Временное разнесение, т. е. передача последовательности импульсов на некоторой постоянной частоте (вобуляция периода повторения), есть не что иное как широко известная время-импульсная модуляция (ВИМ).

Если полагать, что интервалы [0,Т] и [0,W] – представляют собой интервалы соответствующих эффективных значений, то база сигнала В = TW равна площади прямоугольника, заштрихованного на на рис. 6 а, сравнение которой с суммарной площадью заштрихованных зон на рис. 6 б даёт всегда меньшее значение. Другими словами, коэффициент сжатия (база В) при прочих равных условиях непрерывных по времени и частоте истинно хаотических сигналов будет всегда выше, чем соответствующий коэффициент составных псевдошумовых сигналов. Перераспределение координат Т и W в условиях сохранения постоянной базы В = TW = сonst = 25 для произвольных Т и W приводит к тому, что производная W/ = W = -1 и точке Т = W = . Нетрудно показать, что в этом случае форма тела неопределённости удовлетворяет форме круговой симметрии с пиком в точке 0 и окружностью радиусом = 1/ в основании, а В = NМL – число N – где число временных отсчётов, M х L – размер пространственного окна по азимуту и углу места ФАР. Сравнение широкополосности сигналов по частотно –временной диаграмме Рис.6 необходимо осуществлять при одинаковом отношении средней мощности сигнала = Е/Т к мощности шума = W на входе приёмника, т.е. при одинаковом среднем = . Ясно одно, что рандомизация временных и частотных параметров сигнала размывает границы зон частотно-временного распределения ресурса, может привести к увеличению общей зоны покрытии в сравнении с Рис. 6 б и таким образом увеличить базу В (зону покрытия) СШП сигнала, а элементы теории нечётких множеств должны стать новым инструментом в построении общей теории синтеза СШП сигналов для РЛС с СДЦ.

Для реализации сверхразрешения требуется повышать порядок модели сигнала, т.е. расширять спектр несущего сигнала. С некоторой натяжкой можно назвать широкополосными методы, у которых произведение ТW имеет величину значительно большую единицы.

Рандомизация (хаотизация) временных и частотных параметров сигнала размывает границы зон частотно-временного распределения ресурса (см. Рис.6 в), может привести к увеличению общей зоны покрытия прямоугольника WxT в сравнении с Рис. 6 б и таким образом увеличить базу В (зону покрытия) сигнала. Для сравнения многоканальных РЛС с ПВ обработкой с расширением спектра можно использовать следующее понятие обобщённого энергопотенциала

= Р_пер NML/ Р_пред , (9)

где Р_пер – мощность передатчика, Р_пред – чувствительность приёмника, N – размерность временного, а М и L – размерности пространственного окна (М – по азимуту, а L – по углу места).

Заключение

Установлено, что круг рассматриваемых вопросов построения современных РЛС с СДЦ со сниженным уровнем заметности, может быть решен методами стохастической радиолокации. Стохастическая радиолокация в отличие от обычной базируется на концепции внедрения в процесс обработки и формирования сигналов искусственной стохастичности, предполагающей наряду с естественной стохастичностью, обусловленной случайной природой входных сигналов, рандомизацию условий процесса «приём – передача». Введение в процедуры обработки и формирования сигналов контролируемых случайных параметров расширяет спектр сигналов, устраняет стробоскопические эффекты, уменьшает боковые лепестки ДОР цели, снижает требования к разрядности АЦП вплоть до бинарно – знакового квантования.

В статье даётся оценка возможности и перспектив применения псевдошумовых РЛС. Для снижения вероятности перехвата предложено использование в РЛС псевдошумовых хаотических сигналов, применение которых в режимах СДЦ и углометрии из-за несовершенства элементной базы дискретной микроэлектроники ранее считалось невозможным.

Сделан вывод о том, что стохастическая радиолокация может занять промежуточное положение между шумовой НИ (или КНИ) радиолокацией и традиционной высокопотенциальной радиолокацией с составными детерминированными (шумоподобными) сигналами, достигая характеристик близких соответствующим аналоговым прототипам.

Литература

1. Горбунов Ю.Н. Стохастическая радиолокация: условия решения задач обнаружения, оценивания и фильтрации // Электронное издание «Журнал Радиоэлектроники», ISSN1684-1719, - М.: ИРЭ им. В.А. Котельникова РАН, №11, 2014. URL: http://jre.cplire.ru/jre/nov14/3/text.html.

2. Горбунов Ю.Н., Лобанов Б.С., Куликов Г.В. Введение в стохастическую радиолокацию. Учебное пособие для вузов. – М.: Горячая линия-Телеком, 2015. 376 с.: ил.

3. Boulat A. Bash, Dennis Goeckel, Don Towsley. Limits of Reliable Communication with Low Probability of Detection o AWGN Channels. U Mass Technical Report UM. – CS. – 2012. - 003. P. 32.

4. Шеннон К. Работы по теории информации и кибернетики. – М.: Изд. Ин. лит., 1963.

5. Борисов Ю.П., Пенин П.И. Основы многоканальной передачи информации. М.: Связь. – 1967. 435 с.

6. Lukin K.A. // Proc. Inter. Conf. Radar Systems. May 17-21 1999, Brest, France.

7. Guo-Sui Liu, Hong Gu, Wei-Min Su et al. // IEEE Trans. 2003. V. AES-39. №. P. 489.

8. Narayanan R.M., Yi Xu, Hoffineier P.D., Curtis John O. // Optical Engineering. 1998. V. 37. № 6. P. 1855.

9. Hongbo Sun. Yilong Lu, Guosui Liu // IEEE AES Magazine. 2003. V. 18. № 11. P.3.

10. Chapursky V.V., Sablin V.N., Kalinin V.I., Vasilyev I.A. // Proc. 10th Intern. Conf. on Ground Penetrating Radar (GPR-2004). The Netherlands, Delft. June 21-24, 2004. V. I. P. 199.

11. Широкополосные системы связи (обзор). // Зарубежная радиоэлектроника. 1965. № 8.

12. Калинин В.И., Чапурский В.В. Сверхширокополосная шумовая радиолокация на основе антенных решеток с рециркуляцией сигналов // Радиотехника и электроника, 2008, том 53, № 10, с. 1266 – 1277.

13. Горбунов Ю.Н. Рандомизированная обработка сигналов в радиолокации и связи". Монография ISBN 978-3-659-37797-6. - Издательство «LAP LAMBERT Academic Publishing», 66121, Saarbrücken, Germany, 2015, 150 с.

14. Теоретические основы радиолокации. Под ред. Я.Д.Ширмана. Учебное пособие для вузов. – М.: Советское радио, 1970. – 560 с.

15. Горбунов Ю.Н. Стохастическая интерполяция пеленга в адаптивных антенных решетках с последовательным диаграммо-образованием на базе усечённых апертур и робастных статистик сигнала на входе // Издательство «Радиотехника», Журнал «Антенны», 2015, №6, С. 18-26.

16. Горбунов Ю.Н. Принцип стохастического обеления пассивных коррелированных помех в задаче оптимизации систем СДЦ // Информационно-управляющие системы, 2015, №2, С. 15-22.

17. Huffman D.A. The synthesis of linear sequential coding networks. Information theory. Academic Press, New, 1956. P. 77 – 95.