ТРАНСПОРТИРОВКА ПУЧКА С НАЧАЛЬНЫМ ЭЛЛИПТИЧЕСКИМ СЕЧЕНИЕМ ПРИ СОХРАНЕНИИ ЕГО ФОРМЫ
П. И. Акимов1, А. А. Гаврилин1, А. П. Никитин1, В. А. Сыровой2, А. Б. Богословская3
1ФГУП “НПП”ТОРИЙ
2ФГУП “Всероссийский электротехнический институт
3Российский университет дружбы народов
Статья поступила в редакцию 14 октября 2015 г.
Аннотация. Обсуждается проблема транспортировки электронного пучка с эллиптическим сечением при однородном и неоднородном распределении плотности пространственного заряда. Рассчитана конфигурация канала, обеспечивающая сохранение начальной формы пучка.
Ключевые слова: электронный пучок, пространственный заряд, электронно-оптическая система.
Abstract. The problem of transport of electron beam with elliptic cross-section in the case, when the distribution of spatial charge is either homogeneous or nonhomogeneous, is discussed. The configuration of channel providing initial beam form conservation is calculated.
Keywords: electron beam, spatial charge, electron optical system.
В последнее десятилетие появляется множество работ, направленных на создание различных СВЧ-приборов (усилители, клистроны, гиротроны, преобразователи СВЧ-энергии) с ленточными пучками [1–12]. Информация об электронно-оптических системах встречается лишь в некоторых из них [4,9–12], причем, как правило, она представлена рисунками, иллюстрирующими результат использования трехмерных программ траекторного анализа. Линейная компрессия L при этом достигает очень высоких значений (L≳30), что означает необходимость достоверного расчета величин порядка 1/30. С запасом на порядок программы анализа должны иметь ошибку, не превышающую десятых долей процента.
В литературе не встречаются методические исследования, гарантирующие подобную точность численных моделей, в которых вопросы адекватного описания окрестности катода (сингулярной поверхности при эмиссии в ρ- или T-режимах с нулевой скоростью старта электронов) и оси пучка (прямой от пересечения плоскостей симметрии).
Среди цитированных работ не существует единого мнения о том, какова должна быть конфигурация пучка на выходе из ЭОС и соответствия результатов: в [7] отмечено, что прямоугольный катод при компрессии по одной из координат обеспечил почти однородную плотность тока эмиссии J и сохранение прямоугольного сечения пучка; в [5] дана рекомендация по переходу к эллиптическому катоду из-за нарушения формы сечения на торцах (“dumbell distortion”, гантельная конфигурация), которое, по-видимому, сопровождается неоднородностью J; в [2] при изучении диокотронной неустойчивости рассматривается пучок с эллиптическим сечением; в [8] для прямоугольного катода плотность тока на периферии достигает 14 A/см2 при средней плотности 8 A/см2.
Некоторые постановки вызывают определенное удивление. Так, в [5] в качестве наводящих соображений используются результаты по синтезу осесимметричной пушки Пирса вместо плоской пушки с бесконечным ленточным пучком, а достоверность результатов обосновывается совпадением расчетов по двум различным программам анализа. Подобное совпадение свидетельствует только об отсутствии ошибок программирования при одной и той же или близких моделях пучка.
Авторы работы [6] игнорируют основные результаты теории формирования (угол наклона 67.5о нулевого формирующего электрода) и незнакомы с задачами формирования эллиптических и “почти прямоугольных” пучков [13]. Вывод о предпочтении нулевого формирующего электрода в виде прямоугольного короба по сравнению с эллиптическим сечением явно противоречит известным в оптике плотных пучков фактам.
Не менее важной, чем проблема формирования потока, является задача его дальнейшей транспортировки. При этом возможны два варианта, связанные либо с технологичной формой канала (прямоугольное сечение), либо с желанием сохранить начальное эллиптическое сечение потока. В первом случае решение возможно только численными методами [14,15], во втором в их использовании нет необходимости.
Целью
работы является расчет лапласовского поля вне цилиндрического электронного
пучка с эллиптическим сечением и определение конфигурации канала
транспортировки. При произвольном распределении плотности пространственного
заряда 
, где 
определяет
эллиптический контур, решение может быть выписано в квадратурах [16].
В
случае 
для потенциала в пучке 
и лапласовского поля 
вне пучка имеем
(1)
Здесь a,b – полуоси эллипса; x,y – декартовы координаты в плоскости сечения; ξ – корень
Альтернативная
форма решения для основана на использовании метода Римана в случае уравнений
эллиптического типа [13]. Введем эллиптические координаты ξ, η с равными коэффициентами Ляме 
:
(2)
Решение уравнения Лапласа представим в виде:
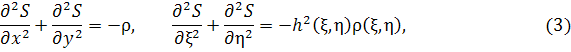
причем функция S удовлетворяет однородным условиям на границе пучка и выражается через двойной интеграл:
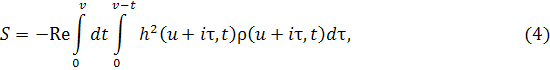
где 
– уравнение границы потока.
Функции под интегралом в (4) претерпели следующие изменения:
(5)
При полиномиальном распределении 
решение удается выразить в элементарных функциях.
Для n-1-го члена
полинома 
или 
имеем
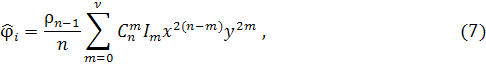
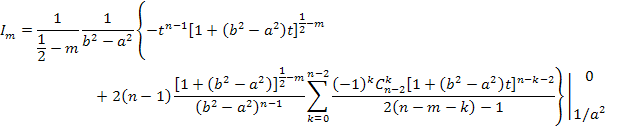
В
выражении для Im
необходимо выполнить для t подстановки
верхнего и нижнего пределов интегрирования; крышка в формуле для означает, что после вычисления последнего члена с m=ν выражение должно быть дополнено
симметричными членами, получающимися из уже выписанных при помощи замен 
.
В случае 
имеем
Фрагменты решения, соответствующие коэффициенту 
в (6), определены формулами
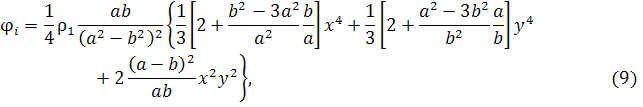
В случае 
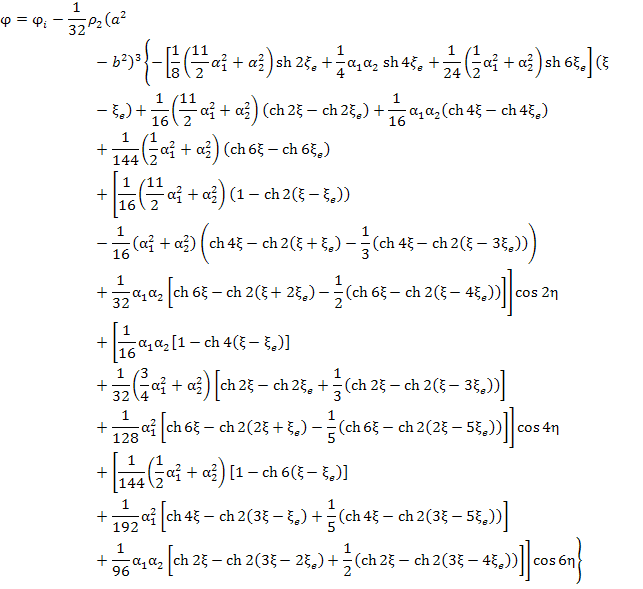
Из формул (8)-(10) видно, что эквипотенциали вне эллиптического пучка всегда содержат азимутальные зависимости, делающие их отличными от эллипсов того же семейства, что и контур сечения.
Исследование случая ρ≠const интересно по следующим соображениям. Вариация плотности пространственного заряда в поперечном сечении является скорее правилом, чем исключением. К ней приводят особенности электронно-оптической системы (при отсутствии магнитного поля криволинейные траектории со сферического катода, необходимые для достижения компрессии, возможны только за счет градиента плотности тока эмиссии в ρ-режиме), необходимость формирования близких к кольцевым структур, поражение эмиссионного слоя в результате ионной бомбардировки при длительной эксплуатации прибора. На рис.1 представлен результат экспериментального исследования последнего эффекта (кривая 1) и близкая в качественном отношении кривая 2, описывающая полином (6) при n=2.
Рис.1 Изменение эмиссионной способности под действием ионной бомбардировки
При повышении температуры катода и наработке в 1500 часов дефицит тока составил около 10%, а поврежденная часть эмиссионного слоя – около 20% поверхности катода. Неоднородный токоотбор будет транслироваться в канал транспортировки.
На рис.2 приведены результаты расчета возможной конфигурации
канала в случае 
при разном отношении полуосей 
пучка (
2,5,10). Эквипотенциальные кривые вне пучка в системе, связанной с его
границей, не являются эллипсами, но могут быть аппроксимированы семейством
эллипсов с отношением полуосей , отличным от соответствующего параметра поперечного
сечения электронного потока.
Эффект изменения плотности по закону
(11)
представлен на рис.3,4.
а)
б)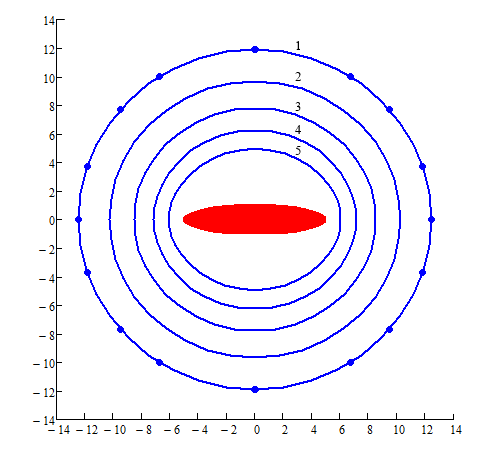
в)
Рис.2 Эквипотенциальные поверхности 
при 
:
а) a/b=2,
1 – 
, 2 – 
, 3 – 
, 4 – 
, 5 – 
.
б) a/b=5, 1 – 
, 2 – 
, 3 – 
, 4 – 
, 5 – 
.
в) a/b=10, 1 – 
, 2 – 
, 3 – 
, 4 – 
, 5 – 
.
Во
всех случаях эквипотенциали вне пучка могут быть аппроксимированы
эллипсоидальными овалами с небольшим отношением полуосей, указанным на рисунках
для ближайшей к пучку и периферической кривых. Последние весьма близки к
окружностям, а точками на них отмечены координаты эллипса с теми же полуосями.
При качественном подобии кривых φ=const при разных значениях распределение потенциала для этих случаев существенно различается.
а)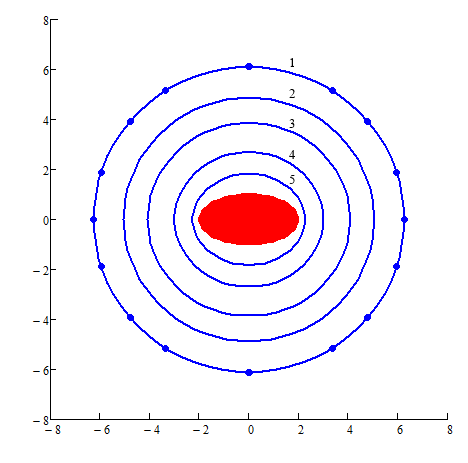
б)
в)
Рис.3 Эквипотенциальные поверхности при 
:
а) a/b=2,
1 – , 2 – 
, 3 – 
, 4 – 
, 5 – 
.
б) a/b=5,
1 – 
, 2 – , 3 – , 4 – 
, 5 – 
.
в) a/b=10, 1 – , 2 – 
, 3 – 
, 4 – 
, 5 – 
.
Отметим, что выполненные в [14] расчеты с использованием
пакета OPERA 3D в относительно простой с вычислительной точки зрения задаче
без сингулярной эмитирующей поверхности не обнаруживают высокой точности: в
симметричной по квадрантам проблеме получено несимметричное распределение параметров
пучка.
В качестве меры по борьбе с искажением формы сечения авторы работы [14] предлагают либо усилить магнитное поле, либо увеличить коэффициент заполнения. Второе предложение не решает проблемы: приближение эллиптической эквипотенциали к неэквипотенциальной поверхности пучка приведет еще к большей деформации последней и высаживанию на стенки канала.
а)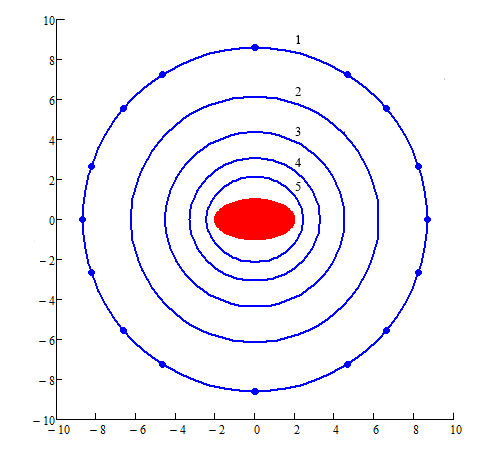
б)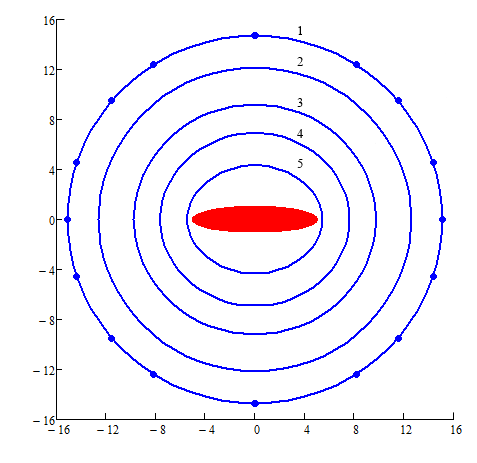
в)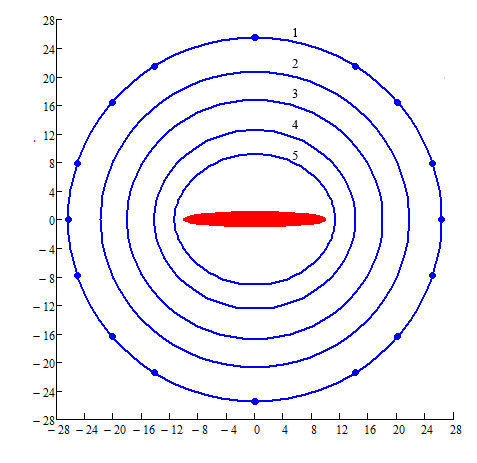
Рис.4
Эквипотенциальные поверхности при 
:
а)– a/b=2, 1 – , 2 – 
, 3 – 
, 4 – , 5 – 
.
б)– a/b=5, 1 – 
, 2 – , 3 – , 4 – , 5 – 
.
в) a/b=10, 1 – 
, 2 – , 3 – , 4 – 
, 5 – 
.
Возмущение эллиптического сечения может быть не только уменьшено, но и устранено в результате перехода к определяемому приведенными выше формулами сечению канала, который с точки зрения технологии не сложнее эллиптического. Магнитное поле, играющее роль стабилизирующего фактора, напротив, может быть ослаблено.
При нормировке потенциала на потенциал анода 
решение уравнения Лапласа на выходе из электронно-оптической системы
можно представить в виде
где 
- отношение полуосей; на рисунках значение потенциала определялось
выражением в квадратных скобках, зависящим только от .
Параметр 
в (12) можно выразить через ток пучка I или среднюю плотность тока 
:
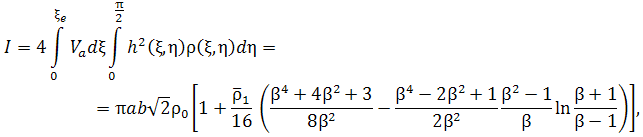
где 
- диэлектрическая постоянная вакуума, 
– удельный заряд электрона, L – характерный масштаб длины
(расстояние катод-анод), V
– характерная скорость 
.
Пересчет маркировки эквипотенциалей на рисунках при нормировке на анодный потенциал производится по формулам (12),(13) при задании размерных значений физических параметров системы.
Заключение
В случае, если
приоритетной задачей является сохранение начальной эллиптической формы пучка,
конфигурация канала определяется приведенными выше выражениями. Форма сечения
тракта транспортировки, близкого к поверхности пучка, хорошо аппроксимируется
эллипсом с отношением полуосей, малым по сравнению с этим параметром для
электронного потока и коэффициентом заполнения, меньшим 0.5, особенно для
сильно вытянутого контура пучка. Вне зависимости от характера распределения
плотности в потоке всегда можно указать удаленную эквипотенциаль, с высокой
точностью совпадающую с окружностью. Для пучка с 
такая эквипотенциаль имеет радиус порядка 20. Сопровождающее магнитное
поле при использовании рассчитанной формы тракта является стабилизирующим
фактором и не тратится на сохранение формы сечения.
Литература
1. Pasaour J., Nguen K., Antonsen T. et al. // IVEC-2009. P.300.
2. Ruan C., Wang S., Han Y. et al. // IEEE Trans. on Electron Dev.2014. V.61 N6 P.1643.
3. Pershing D., Nguen K., Abe D.K. et al. // IVEC-2014. P.121.
4. Cusick M., Atkinson J., Balkcum A. et al.// IVEC-2009. P.296.
5. Jangid S.K., Bandyopadhyay A.K., Joshi L.M. et al. // IVEC-2013. Poster Session III.
6. Tang X., Duan Z., Guo X. et al. // IVEC-2012. P.385.
7. Nguen K.T., Pasaour J., Wright E.L. et al. // IVEC-2008. P.179.
8. Pasaour J., Wright E., Nguen K. et al. // IVEC-2010. P.43.
9. Pasaour J., Nguen K., Wright E. et al. // IEEE Trans. Electron Dev.2011. V.58. NG. P.1792.
10. Levush B., Abe D., Pasaour J. et al. // IRMMW-THz 2014.
11. Pasaour J., Abe D., Nguen K. et al. // IVEC-2014. P.19.
12. Мануилов В.Н., Заславский В.Ю. Глявин М.Ю. и др. // Труды XI Всероссийского семинара “Проблемы теоретической и прикладной электронной и ионной оптики.” 2013.М. : ГНЦ “НПО ОРИОН”. С.55.
13. Syrovoy V.A. Theory of intense beams of charged particles. New York: ELSEVIER, 2011.
14. Panda P.C., Srivastava V., Vohra A. // IVEC-2011. P.299.
15. Tang X., Sha G., Duan Z. et al. // IVEC-2013. Poster Session I.