|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 10, 2002 |
|
Амплитудные поверхности дисперсии замедляющих систем
В.А. Солнцев, e-mail: soln@miem.edu.ru, Д.Ю. Никонов, e-mail: nkv-1999@mtu-net.ru
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
Получена 20 октября 2002 г.
Записаны общие соотношения для пространственных спектров поля в периодических и непериодических замедляющих системах. Введено представление этих спектров в виде амплитуды пространственной гармоники поля как функция двух переменных – частоты и продольного волнового числа или эквивалентных им переменных. Соответствующую поверхность можно рассматривать как амплитудную поверхность дисперсии, гребни которой определяют зоны взаимодействия электронов с полем по скорости и частоте. Получено аналитическое представление амплитудной поверхности дисперсии для отрезка согласованного петляющего волновода, проведен численный расчет таких поверхностей для отрезков замедляющих систем типа цепочек связанных резонаторов и цепочек связанных двузазорных кольцевых резонаторов. Показано влияние ширины зазоров взаимодействия на оптимальную синхронную скорость в конечных отрезках замедляющих систем.
Свойства взаимодействия электронных потоков с замедленными электромагнитными волнами определяются двумя основными характеристиками волн или их пространственных гармоник – замедлением и сопротивлением связи. В периодических замедляющих системах (ЗС) имеется дискретное множество дисперсионных характеристик, определяющих зависимость этих величин от частоты.
При исследовании дисперсионных характеристик замедляющая система, как правило, предполагается бесконечной и строго периодической вдоль продольной оси, что и приводит к дискретному спектру пространственных гармоник [1]. Между тем, в современных ЛБВ и других электронных приборах СВЧ длина отдельных секций может быть сравнительно небольшой и составлять 5-10 периодов системы, а в предложенных недавно [2,3] псевдопериодических (скрытопериодических) ЗС период может вообще отсутствовать и зазоры взаимодействия электронов и поля могут располагаться неэквидистантно для выделения рабочей и подавления паразитных пространственных гармоник. При этом спектр пространственных гармоник размывается, и становиться по существу непрерывным, обычное понятие дисперсионной характеристики теряет свой смысл, а выбор той или иной составляющей пространственного спектра определяется лишь амплитудой этой составляющей.
Дисперсионные характеристики периодических ЗС строятся обычно как кривые в координатах длина волны l – замедление n=с/v или волновое число h – частота w =kc при указании на них соответствующих значений сопротивления связи. В настоящей работе введено представление пространственных спектров волны в виде амплитуды пространственной гармоники плоя Е как функции двух из указанных переменных. Соответствующую поверхность можно рассматривать как амплитудную поверхность дисперсии, гребни которой определяют зоны взаимодействия электронов с полем по скорости и частоте.
2. Спектр пространственных гармоник – общие соотношения
Амплитуды непрерывного спектра пространственных гармоник 
для конечного отрезка ЗС определяются через распределение поля 
преобразованием Фурье
[3]:
где – длина l отрезка ЗС, включающего Q шагов системы (зазоров взаимодействия электронов и поля).
Запишем поле по компонентам:
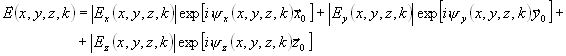
и перейдем в (1) к сумме интегралов по Q шагам. Для простоты ограничимся преобразованием продольной компоненты поля Ez, определяющей взаимодействие поля с прямолинейными потоками электронов. Выражение для спектра амплитуд пространственных гармоник, отличающего от спектральной плотности лишь делением на длину рассматриваемого отрезка системы l, примет вид:
где zq, dq – средняя координата и эффективная ширина q-го зазора, выбор которых до некоторой степени произволен, 
- фаза поля в сечении системы z=zq. Величина
определяет эффективное поле, действующее на электрон с учетом конечного времени его пролета через q-й зазор системы. По аналогии с теорией дискретного взаимодействия электронов и поля в ЛБВ и теорией клистрона введем общее выражение для локального коэффициента взаимодействия (коэффициента формы поля) на q-м шаге системы
где
- поле эквивалентного плоского зазора ширины dq при напряжении Uq таком же, как в реальном q-м зазоре.
В результате выражение (2) для амплитуд пространственных гармоник можно представить в виде
Для коротких отрезков ЗС с небольшим числом зазоров Q (вплоть до Q=1 в резонаторах клистронов) удобно использовать средний коэффициент взаимодействия электронов и поля по всей длине системы:
Вводя среднее по всем зазорам напряжение:
Приведенные соотношения для спектра пространственных гармоник позволяют рассмотреть распределение их амплитуд в зависимости от частоты w =kc и волновых чисел h, сопротивление связи для периодических и скрытопериодических замедляющих систем ЛБВ, коэффициент взаимодействия для резонаторов клистронов.
Ниже приведён ряд случаев, позволяющих рассмотреть характерные закономерности поведения спектров пространственных гармоник.
3. Петляющий волновод - аналитические соотношения
Рис.1 Отрезок периодического петляющего волновода.
Рассмотрим согласованный отрезок периодического петляющего волновода (рис. 1), который может служить также моделью ЗС типа цепочек связанных резонаторов (ЦСР). В простейшем случае, считая, что параметры волновода не изменяются по длине, отражений от изгибов нет и, выделяя в (2) четные и нечетные зазоры с геометрическим поворотом фазы поля на p , имеем:
zqº
D(q-1), Uqº
U(k), 
, 
,
где q=1,2, …Q, 
набег фазы вдоль изогнутого отрезка волновода длины S на шаге D по центру системы x=y=0, 
- волновое число в волноводе. Подставляя это выражение в (6) и полагая для нечетных членов q=2р-1, для четных q=2р, p=1,2, … Q/2, получим:
В бесконечной ЗС (Q®
¥
) волновое число 
для m-й пространственной гармоники определяется соотношением
, m=0,±
1, ±
2, …
в котором для рассматриваемой системы период L=2D, так что
В результате для амплитуд дискретного спектра пространственных гармоник при учете l=QD получаем:
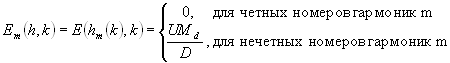
Используя условие (8), преобразуем выражение (7) для отрезка системы к виду
Рабочими являются нечетные гармоники, для них после суммирования в (9) геометрической прогрессии можно получить:
причем для плоского зазора шириной d без учета частотной зависимости полей в нем имеем известное выражение:
Выражения (10),(11) определяют поведение поверхности 
над плоскостью h,k. Если d→0, то Md→1 и гребни функции соответствуют обычным дисперсионным характеристикам h=hm(k), однако они имеют конечную ширину, определяемую длиной отрезка ЗС l=DQ; при Q→∞ гребни бесконечно тонкие и получается дискретный спектр дисперсионных характеристик. Если же учесть ширину зазора при конечном Q, то гребни сдвигаются по h под влиянием Md(h), т.е. изменяется синхронная скорость vQ=ck/hQ. Величина этого сдвига невелика, её грубая оценка получается из (10),(11):
Вводя сопротивление связи обычным образом, можно определить его во всей плоскости h, k:
где 
- характеристическое сопротивление волновода, j
=hl/Q – набег фазы пространственной гармоники на один шаг, 
- средний коэффициент взаимодействия электронов и поля на Q шагах.
Расширение спектра волновых чисел при уменьшении Q приводит к возможности одновременного взаимодействия с электронным потоком группы пространственных спектральных составляющих поля находящихся в зоне усиления ЛБВ:
,
где С –параметр усиления, 
- электронное волновое число. Поэтому обычная одноволновая линейная и нелинейная теория ЛБВ при достаточно коротких отрезках отрезков секций Q<10 должны применяться с осторожностью даже в случае идеального согласования секций.
В то же время теория дискретного взаимодействия справедлива при любых Q, в частности для одного резонатора Q=1, когда спектр волновых чисел гармоник, определенный для плоского зазора соотношением (11), имеет большую ширину, превышающую зону усиления ЛБВ.
4. Амплитудные поверхности дисперсии для отрезков ЦСР
Для расчета спектра пространственных гармоник использовалась программа ISFEL3D [4], позволяющая рассчитывать резонансные частоты, волновое сопротивление и коэффициент формы для отрезков ЗС.
Рассчитывалась функция
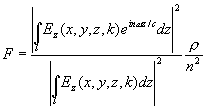
характеризующая действующую на электроны спектральную составляющую поля, взятую на частоте w с волновым числом h=w n/c при замедлении n=c/v; r -волновое сопротивление отрезка системы. Через эту функцию можно вычислить сопротивление связи (13).
Для расчета F при фиксированной в полосе прозрачности частоте w =kc менялось замедление n=c/v=h/k и проводился пространственный Фурье-анализ поля.
1. Обычная система типа цепочек связанных резонаторов (ЦСР) показана на рис. 2. На рис. 3 приведены дисперсионные характеристики системы, рассчитанные по обычной методике, без учета ограниченности её длины. На рис. 4 показаны результаты расчета линий уровня функции F для отрезка из шести резонаторов.
Видно, что гребни функции примерно соответствуют дисперсионным характеристикам рис. 2, однако функция имеет конечное значение так же в окрестности этих характеристик. Поэтому ширина зоны взаимодействия электронного потока и поля по скорости и частоте будет определяться не только параметром усиления, но и размытостью этих характеристик.
2. Система типа цепочек связанных двузазорных кольцевых резонаторов [5] (ЦСДКР) показана на рис. 5. На рис. 6 приведены дисперсионные характеристики системы, рассчитанные по обычной методике, без учета ограниченности её длины. На рис. 7 показан результат расчета поверхности F для отрезка из десяти резонаторов.
Построение амплитудных поверхностей дисперсии проиллюстрировано здесь на примере отрезков периодических ЗС.
Размытее спектра пространственных гармоник обусловлено при этом ограниченностью длины отрезка системы.
Значительно более существенным может быть размытее и трансформация спектров пространственных гармоник в неоднородных системах. В частности, исследования пространственных спектров для скрытопериодических систем при фиксированной частоте показало возможность подавления паразитных пространственных гармоник при сохранении рабочей пространственной гармоники [2,3]. Использование амплитудных поверхностей дисперсии дает возможность эффективного исследования свойств таких систем в полосе частот.
Работа выполнена при поддержке гранта РФФИ №01-02-16703 и гранта поддержки ведущих научных школ РФ №00-15-96-716.
Рис. 2 Замедляющая система типа цепочка связанных резонаторов (ЦСР).
Рис. 3 Дисперсионная характеристика ЗС ЦСР, изображенной на рис. 2.
Рис. 4 Линии уровня амплитудной поверхности дисперсии для отрезка из
6 резонаторов ЗС типа ЦСР, изображенной на рис. 2.
Рис. 5 Замедляющая система типа цепочка двухзазорных кольцевых резонаторов (ЦСДКР).
Рис. 6 Дисперсионная характеристика системы ЦСДКР изображенной на рис. 5.
Рис. 7 Амплитудная поверхность дисперсии системы ЦСДКР, изображенной на рис. 5.
 |
 |
, (1)
, (2)
, (3)
, (4)
, (5)
, (6)
, (7)
(8)
,(9)
, (10)
. (11)
(12)
, (13)
