УДК 621.391.96

МЕТОДИКА ОЦЕНИВАНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК БЛОКОВЫХ ТУРБО-КОДОВ

Л. Е. Назаров, И. В.  Головкин

Институт радиотехники и электроники им. В.А.Котельникова РАН, г.Фрязино

Получена 21 октября 2009 г.

Приведена методика оценивания вероятности ошибочного приема кодовых слов для класса блоковых турбо-кодов. Основу этой методики составляет применение верхней мультипликативной границы в совокупности с усредненным множеством коэффициентов взаимных корреляций между сигналами.

Ключевые слова: блоковые турбо-коды, вероятность ошибки, верхняя аддитивная граница, верхняя мультипликативная граница

 

Введение

Кодовые конструкции под общим названием турбо-коды представляют альтернативу известным помехоустойчивым кодам относительно их вероятностных характеристик [1]. В настоящее время они рассматриваются как наиболее перспективные для использования в системах передачи информации различного назначения [2]. При увеличении информационных блоков турбо-кодов до несколько тысяч битов достигаются вероятностные характеристики при декодировании, близкие к характеристикам Шенноновской пропускной способности каналов с аддитивным белым гауссовским шумом [1].

Для турбо-кодов актуальна проблема оценивания вероятности ошибочного приема кодовых слов . Наличие соответствующего математического аппарата позволяет выполнить теоретическую оценку , не осуществляя трудоемких вычислительных экспериментов.

Наиболее полно проблема вычисления вероятностей  решена для модели канала с аддитивным белым гауссовским шумом и правила приема сигналов, реализующего критерий максимального правдоподобия [3]. Однако даже для такой относительно простой модели канала формульные соотношения расчета вероятности  известны лишь для частных случаев ансамблей сигналов, например, для ансамблей ортогональных сигналов [3].

Вследствие сложности вычисления точных значений вероятностей  в приложениях используются их оценки [3]. Основу методик оценивания составляют соотношения для нижних и верхних границ, например, аддитивная граница [3], ряд тангенциальных границ [4], мультипликативная граница [5]. При их использовании необходимо знание полного множества коэффициентов взаимных корреляций между сигналами.

В статье рассматривается методика оценивания  для класса блоковых турбо-кодов [6]. Данные турбо-коды широко применяются в системах связи и являются базовыми для ряда интернациональных протоколов передачи информации [2], например, для протоколов IESS, разработанных для спутниковой системы связи Intelsat, а также в виде опционального применения в протоколе IEEE 802.16, разработанного для высокоскоростных беспроводных широкополосных сетей передачи в городских сетях.

Предлагаемая методика оценивания вероятностей  для рассматриваемых блоковых турбо-кодов основана на применении верхней мультипликативной границы и использовании усредненного множества коэффициентов взаимных корреляций между сигналами [7], вычисление которого является существенно более простой проблемой по сравнению с проблемой вычисления точного множества коэффициентов взаимных корреляций между сигналами. По отношению к известным границам мультипликативная граница характеризуется точностью производимых оценок и низкой сложностью вычисления [5].

 

1. Постановка задачи

На рис.1 приведена блок-схема кодера блокового турбо-кода на основе двух составляющих кодов  и  [6]. Блоковые турбо-коды подобны каскадным схемам кодирования - последовательность информационных символов поступает на вход кодера внешнего кода , последовательность кодовых символов которого после перемежения поступает на вход кодера внутреннего кода . Внешний код  содержит  эквивалентных блоковых кодов (). Внутренний код  содержит  эквивалентных блоковых кодов (). Здесь  - длительность кодовых слов кода (), - -размерность кода,  - минимальное расстояние Хэмминга.
 

 

Рис.1. Блок-схема формирования блокового турбо-кода.

 

При использовании перемежителей блокового типа рассматриваемые турбо-коды тождественны известным в литературе кодам-произведениям, кодовые слова которых представляются в виде двумерной матрицы [8]. Строки матрицы - кодовые слова кода , столбцы матрицы - кодовые слова кода . Длительность кодовых слов кода-произведения равна , информационный объем , кодовая скорость , минимальное расстояние Хэмминга .

При использовании метода приема сигналов на основе блоковых кодов, реализующего правило максимального правдоподобия, вероятностной характеристикой является вероятность ошибки на сообщение . В этом случае при наличии в канале аддитивного белого гауссовского шума с односторонней спектральной плотностью  вероятность ошибки  зависит от отношения сигнал/помеха  и матрицы нормированных коэффициентов взаимных корреляций между сигналами ,  [3]. Здесь  - объем кодовых слов,  - энергия сигналов. Для сигналов, соответствующих групповым блоковым кодам (к этому классу принадлежат блоковые турбо-коды), вероятность  не зависит от передаваемого кодового слова и определяется спектром расстояний Хэмминга кодовых слов {}, , или множеством взаимных корреляций {} между сигналом, соответствующим нулевому кодовому слову, и другими сигналами из ансамбля [9]. Здесь  - количество кодовых слов с весом Хэмминга . Для сигналов с двоичной фазовой модуляцией, формируемых на основе двоичных блоковых кодов, коэффициенты взаимной корреляции  линейно связаны с весом Хэмминга  соответствующего кодового слова соотношением . Вероятность  для множества {} обозначим .

Выражение для  в общем случае эквивалентно многомерному интегралу ошибок, его вычисление представляет сложную проблему. Поэтому в приложениях применяют его оценки в виде верхних границ, наиболее известными из которых являются аддитивная граница [3], класс тангенциальных границ [4] и мультипликативная граница [5].

Верхняя аддитивная граница имеет вид [3]

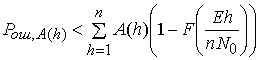.                               (1)

Здесь 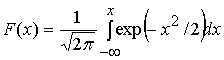 - одномерный интеграл ошибок.

Тангенциальные границы являются более точными по отношению к аддитивной границе (1). Наиболее простая тангенциальная граница Галлагера-Бэрлекэмпа задается соотношением [4]

,         

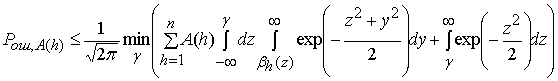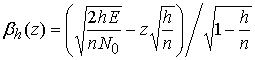.                                (2)

Граница Галлагера-Бэрлекэмпа (2) и мультипликативная граница сравнимы по точности производимых оценок, однако вторая характеризуется существенно меньшей сложностью при вычислении. Она имеет вид [5]

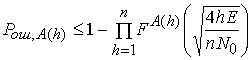.                                 (3)

Разработка методики оценивания вероятности ошибки  для блоковых турбо-кодов с использованием мультипликативной границы (3) составляет суть рассматриваемой проблемы.

 

2. Оценивание вероятности ошибки блоковых турбо-кодов

Определение спектра {} для блоковых турбо-кодов представляет сложную проблему. Разработанные методики его вычисления имеют ограниченную продуктивность - аналитические соотношения дают возможность определения лишь подмножества {} множества {}. В работе [10] приведено соотношение для вычисления подмножества {} для блоковых турбо-кодов на основе двух блоковых кодов (), () и множествами {}, {}

.                                             (4)

Суммирование в (4) производится по делителям  значения . Соотношение (4) применяется для вычисления  в диапазоне

 

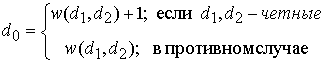,                            (5)

Здесь ,  - наименьшее целое, большее или равное .

При определении функции  для составляющего блокового кода можно применять известные методы на основе спектра весов дуального кода [8]. Например, для расширенных кодов Хэмминга () значение веса  равно коэффициенту при  в составе многочлена [8] , .

В работе [7] предложена методика оценивания  для турбо-кодов, не требующая множества {}. Эта методика основана на использовании усредненного спектра {}, формируемого с использованием модели случайного перемежителя в схеме кодера блоковых турбо-кодов (рис.1). Данная модель перемежителя осуществляет отображение последовательности кодовых символов длительностью  и весом  внешнего кода  во все возможные последовательности на входе внутреннего кода  с вероятностями . В результате действия данной модели результирующим является усредненное по возможным перемежителям множество {} с элементами

Аддитивная граница и граница Галлагера-Бэрлекэмпа обладают свойством  - выпуклости, поэтому для них выполняется неравенство Йенсена относительно усредненной вероятности ошибки  при использовании модели случайного перемежителя [9]

.                                                 (6)

Здесь  - вероятность турбо-кода со спектром кодовых слов {}.

При вычислении {} для блоковых турбо-кодов на основе блоковых кодов  () и  () используют соотношение 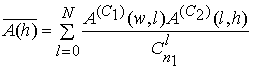[7]

.                                 (7)

Множители  в (7) соответствуют множителям при переменных  в многочлене , множители  соответствуют множителям при переменных  в многочлене . Многочлен от переменных  для блокового кода с параметрами () имеет вид 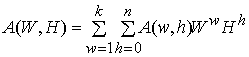, здесь  - количество кодовых слов с весом Хэмминга  и с весом информационной последовательности, равным .

Для расширенных кодов Хэмминга () значения  задаются соотношением, используя полиномы 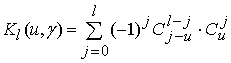 [12]

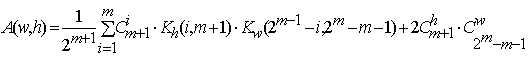.      (8)

Докажем, что верхняя мультипликативная граница также обладает свойством  - выпуклости и для этой границы выполняется неравенство Йенсена (6). Сделаем предварительные замечания.

Пусть  - вектор, компоненты которого являются значения спектра весов {} произвольного блокового линейного кода с параметрами (). Компоненты  принимают значения в диапазоне  и для них справедливо соотношение .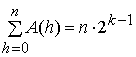

Утверждение. Область  векторов  для возможных блоковых кодов () является  - выпуклой, то есть для любых векторов  и  из  и для любого значения  выполняется условие .

Действительно, компоненты вектора удовлетворяют требуемым условиям  и .

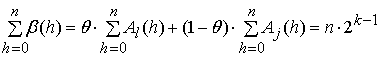Определение [9]. Функция , определенная на выпуклой области  векторов  и принимающая действительные значения, называется  - выпуклой, если для любых векторов , и для любого значения  верно условие .

Утверждение. Мультипликативная граница (3) является  - выпуклой для введенного выше вектора .

Доказательство. В соответствии с (4) имеем 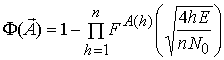, требуется доказать неравенство . Здесь 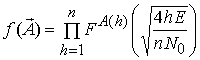. Справедливы следующие соотношения [9]

.

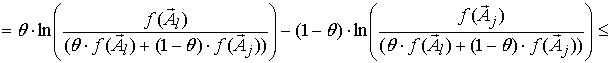
Здесь использовано неравенство . Утверждение доказано.

Таким образом, мультипликативная граница (3) для множества взаимных корреляций {} (7), усредненных по всем возможным перемежителям, определяет верхнюю границу для вероятности ошибки  (6) при приеме блоковых турбо-кодов, также усредненной по всем возможным перемежителям.

Отсюда следует, что существует, по крайней мере, один детерминированный перемежитель в составе блокового турбо-кода, обеспечивающий вероятность ошибки, ограниченной условием .

Проблема выбора оптимальных перемежителей рассматривалась в ряде работ [11]. Исследования показывают, что перемежители блокового типа для рассматриваемых турбо-кодов являются практически оптимальными – их использование обусловливает незначительные энергетические потери (не превышающие 0.2 дБ) по отношению к наиболее эффективным схемам перемежения [1]. Вместе с тем, перемежители блокового типа характеризуются низкой сложностью исполнения средствами цифровой техники, что определяет перспективность их использования. Ниже приведены результаты применения рассматриваемого метода оценивания вероятностей ошибки для ряда блоковых турбо-кодов на основе перемежителей этого типа.

В качестве примера на рис.2 приведен вид усредненного спектра {} для блокового турбо кода с параметрами (256,121,16), формируемого на основе расширенного блокового кода Хэмминга (16,11,4) и вычисленного с использованием соотношения (7).

 

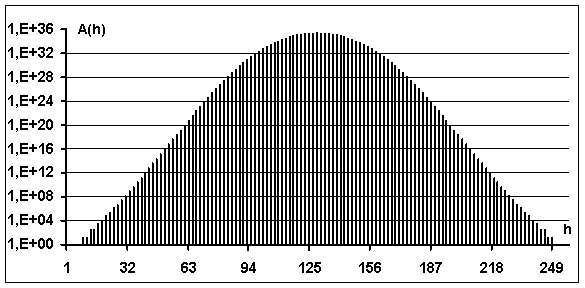
Рис.2 Усредненный спектр весов Хэмминга для блокового турбо-кода (256,121,16) на основе расширенного кода Хэмминга (16,11,4).

 

Следует отметить, что существует отличие между точным значением минимального веса Хэмминга блоковых турбо-кодов и значением минимального веса Хэмминга в усредненном множестве {}. Для рассматриваемого блокового турбо-кода точное значение минимального веса Хэмминга в составе подмножества  размером  (), вычисленного с использованием соотношений (4), (5), равно . Вместе с тем минимальный вес Хэмминга в усредненном множестве {} равен 10. Минимальный вес Хэмминга кодовых слов является важной характеристикой блоковых кодов, так как он определяет асимптотическое поведение вероятности  для больших значений сигнал/помеха.

 

3. Результаты вычислений

Апробация приведенной методики выполнена при исследовании вероятностных характеристик для ряда блоковых турбо-кодов. Сравнивались теоретические вероятностные кривые и экспериментальные кривые, полученные путем компьютерного моделирования алгоритма приема блоковых турбо-кодов. Суть алгоритма приема - итеративная обработка сигналов, ее основу составляет вычисление функционалов от апостериорных символьных вероятностей на текущей итерации и использование значений функционалов в качестве априорных символьных вероятностей на следующей итерации [1]. Этот алгоритм является подоптимальным, его применение обусловливает энергетические потери по отношению к алгоритму оптимального приема.

В качестве примера на рис.3, рис.4 приведены вероятностные кривые, соответствующие турбо-коду с параметрами (256,121,16) на основе рассмотренного выше кода Хэмминга (16,11,4) и турбо-коду (1024,626,16) на основе расширенного кода Хэмминга с параметрами (32,26,4). По оси абсцисс отложены значения сигнал/помеха ,  - энергия сигналов на информационный бит.

 

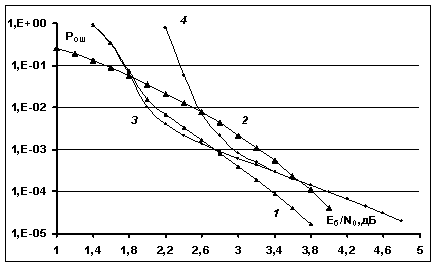
Рис.3. Вероятностные характеристики для турбо-кода (256,121,16) на основе последовательного объединения ансамблей сигналов, соответствующих расширенному коду Хэмминга (16,11): 1 - использование модифицированного множества {} и мультипликативной границы; 2 – экспериментальная кривая; 3 - использование множества {} и мультипликативной границы; 4 - использование множества {} и аддитивной границы.

 

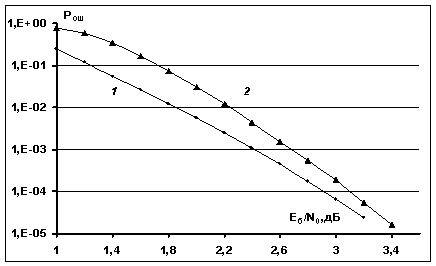
Рис.4. Вероятностные характеристики для турбо-кода (1024,626,16) на основе последовательного объединения ансамблей сигналов, соответствующих расширенному коду Хэмминга (32,26,4): 1 - использование модифицированного множества {} и мультипликативной границы; 2 – экспериментальная кривая.

 

Кривые 3 и 4 на рис.3 соответствуют теоретическим кривым, полученным при оценивании  на основе усредненного множества {} (7) и применении мультипликативной границы (кривая 3) и аддитивной границы (кривая 4). Видно, что для значений  дБ кривая, соответствующая применению методики на основе мультипликативной границы (кривая 3), является более точной по отношению к применению методики на основе аддитивной границы (кривая 2). При увеличении сигнал/помеха эти вероятностные кривые практически совпадают.

Для значений  дБ теоретические кривые являются достаточно грубыми по отношению к экспериментальной кривой (кривая 2) - кривые асимптотически расходятся. Как отмечено выше, это обусловлено влиянием на поведение теоретических кривых значения минимального веса Хэмминга в усредненном множестве {}, который имеет существенно меньшее значение по отношению к точному значению, определяющему поведение экспериментальной кривой.

Улучшение производимых оценок  возможно путем дополнения множества {} точным подмножеством {}, вычисленным с использованием соотношений (4), (5) (кривая 1 на рис.3). Дополнение осуществляется в соответствии с правилом  для , для  значения  остаются неизменными (для рассматриваемых турбо-кодов верно условие ). Из рис.3, рис.4 видно, что при использовании модифицированного множества {} и мультипликативной границы теоретические кривые (кривые 1) для данных турбо-кодов близки к экспериментальным кривым (кривые 2). Можно также заключить, что для анализируемых значений сигнал/помеха энергетические потери при использовании алгоритма итеративного приема рассматриваемых турбо-кодов достигают значений от 0.2 дБ до 0.4 дБ по отношению к оптимальному приему, реализующему правило максимального правдоподобия. При увеличении значений сигнал/помеха значения энергетических потерь уменьшаются.

 

Заключение

Приведена методика оценивания вероятности ошибочного приема кодовых слов для блоковых турбо-кодов. Предлагаемая методика основана на применении верхней мультипликативной границы и использовании усредненного множества коэффициентов взаимных корреляций между сигналами (или его модификации). Вычисление этого множества является существенно более простым по сравнению с вычислением точного множества коэффициентов взаимных корреляций между сигналами. По отношению к известным границам мультипликативная граница характеризуется высокой точностью производимых оценок и низкой сложностью вычисления.

 

Литература

1. Hagenauer J., Offer E., Papke L. Iterative decoding of binary block and convolutinal codes.// IEEE Transactions on Information Theory.1996. V.42. №2. P.429-448.

2. Solemani M.R., Gao Y., Vilaipornsawai U. Turbo coding for satellite and wireless communications. New York. Kluwer Academic Publishers. 2002.

3. Коржик В.И., Финк Л.М., Щелкунов Н.Н. Расчет помехоустойчивости систем передачи дискретных сообщений. М.: Радио и связь. 1981.

4. Herzberg H., Poltyrev G. Techniques of bounding the probability of decoding error for block coded modulation structures.// IEEE Transactions on Information Theory. 1994. Vol. IT-40. №3. P.903-911.

5. Назаров Л.Е. Вероятностные характеристики при оптимальном посимвольном приеме сигналов, соответствующих двоичным блоковым кодам. // Радиотехника и электроника. 1999. Том 44. №10. Стр. 1231-1235.

6. Pundiah R.M. Near-optimum decoding of product codes: block turbo-codes. // IEEE Transactions on Communication. 1998. V.46. №8. P.1003-1010.

7. Benedetto S., Montorsi G. Unveiling turbo-codes: some results on parallel concatenated coding schemes.// IEEE Trans. Inform. Theory. 1996. V.42. №2. P.409-429.

8. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. Перев. с англ. М.: Мир. 1964.

9. Витерби А.Д., Омура Дж.К. Принципы цифровой связи и кодирования. Перев. с англ. М. Радио и связь. 1982.

10. Tolhuizen L. More results on the weight enumerator of product codes.// IEEE Trans. Inform. Theory. 2002. V.48. №9. P.2573-2577.

11. Giulietti A., Perre L., Strum M. Parallel turbo coding interleavers: avoiding collisions in accesses to storage elements.//Electronics Letters. 2002. Vol.38, №5. P. 232-234.

12. Sason I., Shamai S. Bounds on the error probability of ML decoding for block and turbo-block codes.// Annals of Telecommunications. Vol. 54. №3-4. P.183-200.