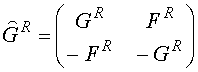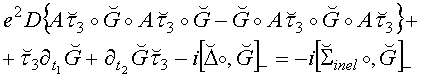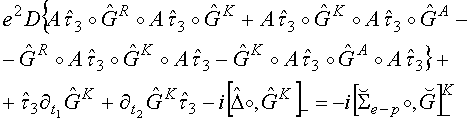“ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ” N 10, 2011

оглавление

ПОГЛОЩЕНИЕ ТЕРАГЕРЦОВОГО ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ В «ГРЯЗНОЙ» СВЕРХПРОВОДНИКОВОЙ ПЛЁНКЕ ПРИ ПРОИЗВОЛЬНОМ ВИДЕ СПЕКТРАЛЬНЫХ ФУНКЦИЙ

 

А. В. Семенов1, И. А. Девятов2, С.А. Рябчун1, С.Н. Масленников1, А.С. Масленникова1, П.А. Ларионов1, Б.М. Воронов1, Г.М. Чулкова1

1 Московский педагогический государственный университет

2 НИИЯФ им. Д. В. Скобельцина МГУ им. М.В. Ломоносова

 

Получена 6 октября 2011 г.

 

Аннотация. В технике Келдыша рассмотрена задача о поглощении мощности высокочастотного электромагнитного поля в сверхпроводнике, удовлетворяющем условию грязного предела. Получено выражение для члена источника в кинетическом уравнении для функции распределения квазичастиц, справедливое при произвольном виде спектральных функций. Этот результат имеет значение для развития последовательной микроскопической теории сверхпроводниковых детекторов излучения терагерцового диапазона, в частности, перспективных детекторов на кинетической индуктивности смещённой током сверхпроводниковой полоски и джозефсоновской индуктивности туннельного контакта.

Ключевые слова: терагерцовое электромагнитное излучение, сверхпроводники, детекторы терагерцового диапазона.

Abstract. A problem of absorption of high-frequency electromagnetic field in dirty superconductor is treated within Keldysh technic. Expression for the source term in the kinetic equation for quasiparticle distribution function is derived. The result is significant for deriving a consistent microscopic theory of superconducting detectors for terahertz frequency range, perspective detectors on kinetic inductance of current-biased superconducting strip and on Josephson inductance of tunnel.

Keywords: terahertz electromagnetic radiation, superconductors, detectors of  terahertz range.

 

Современные наблюдательные задачи радиоастрономии предъявляют исключительно жёсткие требования к уровню шумов детекторов терагерцового диапазона [1, 2]. Одним из наиболее перспективных способов удовлетворить этим требованиям является использование индуктивного отклика сверхпроводниковой полоски или структуры с туннельными контактами, охлаждённой до температуры, много меньшей величины сверхпроводниковой щели. Этим достигается как уход от шумов Найквиста, так и сильное подавление генерационно-рекомбинационных шумов [3]. При этом при реально достижимых рабочих температурах (не ниже 100 мК) величина сверхпроводниковой щели оказывается сравнимой с частотой принимаемого сигнала, что требует последовательного учёта сверхпроводимости абсорбера при описании поглощения электромагнитной мощности.

Задача о поглощении электромагнитного излучения в сверхпроводнике  была решена Элиашбергом [4] для случая вида спектральных функций, следующих из теории БКШ. Однако спектральные функции сверхпроводниковых абсорберов реактивных детекторов могут сильно отличаться от рассчитываемых по теории БКШ: для детектора на индуктивности сверхпроводниковой полоски – из-за модифицирующего действия сверхтока, которым смёщён абсорбер, а для детектора на джозефсоновской индуктивности – из-за туннелирования куперовских пар из сверхпроводниковых берегов. Кроме того, в [4] использован метод аналитического продолжения функций Грина, полученных в технике Мацубары, на действительную ось энергий, в то время как сегодня для описания неравновесных явлений в сверхпроводниках получил распространение метод [5], основанный на решении уравнений для функций Грина в технике Келдыша. Эти обстоятельства делают необходимым рассмотрение задачи о поглощении электромагнитного излучения в сверхпроводнике в случае произвольного вида спектральных функций и с использованием общепринятой сегодня техники [5], которому и посвящена настоящая работа. Мы ограничимся случаем «грязных» сверхпроводников, длина свободного пробега ℓ в которых удовлетворяет условию диффузного предела ℓ<<vF/Δ (vF – скорость Ферми, Δ - параметр порядка). По технологическим причинам, тонкие сверхпроводниковые плёнки, из которых изготавливаются детекторы, практически всегда удовлетворяют этому условию.

Состояние диффузного сверхпроводника в квазиклассической технике может быть описано квазиклассической функцией Грина  – матрицей в прямом произведении пространств Келдыша и Намбу. Её структура в пространстве Келдыша

.                                                                                         (1)

Компоненты  представляют собой матрицы в пространстве Намбу и связаны между собой соотношениями, вытекающими из их аналитических свойств

,                                                                               (2)

.                                                                                     (3)

Матричная функция Грина удовлетворяет уравнению Узаделя [6]:

.                                  (4)

Зависимость от пространственной координаты предполагается устранённой посредством калибровочного преобразования, что всегда возможно сделать в пространственно-однородном случае в отсутствие диссипации. Обозначения следующие: А – вектор-потенциал электромагнитного поля (скалярная величина в силу одномерности задачи);

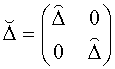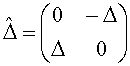, , Δ – параметр порядка,

 - собственно энергетическая часть, описывающая неупругие процессы с квазичастицами, D – коэффициент диффузии.

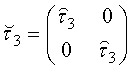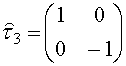,  - матрица Паули в пространстве Намбу; ° означает свёртку по внутренней временной переменной,

,                                                        (5)

;                                                                  (6)

означают дифференцирование по t1,2, [ , ]- - коммутатор.

Функция Грина удовлетворяет также условию нормировки:

.                                                                  (7)

При выполнении условия T0<<τΔ (T0 – характерное время изменения электромагнитного поля, τΔ – время отклика параметра порядка) можно считать  не зависящими от суммарного времени T= ½(t1+t2); в этом приближении Δ=const.

Кинетическое уравнение на функцию распределения квазичастиц получается из келдышевской части уравнения (4).

.                    (8)

Левую часть уравнения (8) описывает рождение квазичастиц электромагнитным полем. Для получения кинетического уравнения удобно перейти от двухвременного к частотно-энергетическому представлению (E,ω) посредством преобразования Фурье по разностному t=t1-t2 и суммарному T= ½(t1+t2) временам:

.                                            (9)

При этом конволюции выглядят так:

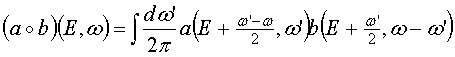,                        (10)

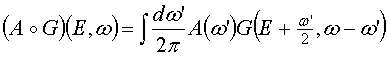;                                     (11)

, . При расписывании конволюций учтём, что, в силу независимости  и  от суммарного времени T,

,                                                             (12)

.                                                                                     (13)

Воспользуемся также стандартной декомпозицией для :

 ,                                                                        (14)

где «матрица распределения»  диагональна, . С учётом (10) и (12) декомпозицию (14) можно переписать так

.                    (15)

Члены в фигурных скобках приобретают теперь следующий вид:

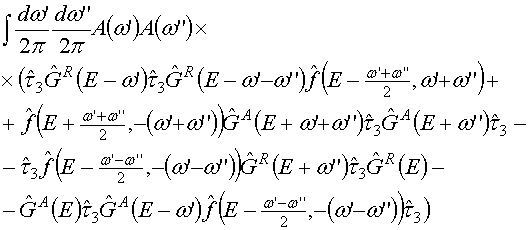          (16)

(положено ω=0).

Пусть падающее излучение монохроматично, . После выполнения интегрирований выражение (16) будет представлять собой сумму 16 слагаемых, в половине из которых частотный аргумент у  равен 0, а в половине ±2ω0. Этими последними можно пренебречь [4]. Учтя также, что в силу частично-дырочной симметрии задачи fT=0, возьмём след по индексам пространства Намбу и получим

.                      (17)

Здесь

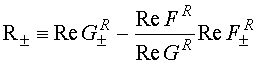                                                                (18)

(при взятии следа были задействованы соотношения (2), (3)) и введены обозначения типа , .

Два других члена в левой части уравнения (8) при ω=0 сводятся к коммутаторам и при взятии следа обращаются в ноль.

С точностью до множителя формула (17) представляет собой выражение для электрон-фотонного источника в кинетическом уравнении для функции распределения квазичастиц. Множитель необходимо ввести для того, чтобы выражение имело смысл производной по времени от функции распределения квазичастиц. (Следует иметь в виду, что функция распределения квазичастиц f связана с величиной fL, также часто называемой функцией распределения, соотношением ).

 

Работа выполнена при поддержке Министерства образования и науки, мероприятие 2011-1.9-519-005, государственный контракт № 11.519.11.4005, и в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013.

 

Литература

 

1.     Poglitsch, A., Altieri, B., in proc. of “Astronomy in the Submillimeter and Far Infrared Domains with the Herschel Space Observatory”, L. Pagani and M. Gerin (eds), EAS Publications Series, 34, 43, 2009.

2.     Nakagawa, T., Murakami, H. Adv. Space Res. 40, 679, 2007.

3.     Sergeev A. V., Mitin V. V., Karasik B. S. Ultrasensitive hot-electron kinetic-inductance detectors operating well below the superconducting transition// Appl. Phys. Lett. 80, 817, 2002.

4.     Элиашберг Г. М. К теории высокочастотной проводимости сверхпроводников. ЖЭТФ 61, 1254, 1971.

5.     Ларкин А. И., Овчинников Ю. Н. Нелинейные эффекты при вязком движении вихрей в сверхпроводниках. ЖЭТФ 73, 299, 1977.

6.     Usadel K. D. Generalized diffusion equation for superconducting alloys //Phys. Rev. Lett. 25, 507, 1970.