УДК 389:621.391:621.396
«ЦВЕТОВАЯ» МОДЕЛЬ РАСПРЕДЕЛЕНИЙ
Ю. Н. Кликушин, В. Ю. Кобенко, А. С. Колмогоров
Омский государственный технический университет
Получена 1 сентября 2011 г.
Аннотация. Описана модель, предназначенная для измерения формы распределения мгновенных значений сигналов. Принцип действия модели основан на преобразовании исследуемого сигнала в цветовой вектор RGB-шкалы. Подобное представление создает основу для формального описания операций с распределениями с помощью аналитического аппарата «цветовой» алгебры.
Ключевые слова: алгебра распределений, измерение формы, RGB-шкала, сравнение сигналов, цветовая модель.
Abstract. A model designed to measure the shape of the distribution of instantaneous values of signals. The operating principle of the model based on the transformation of the signal vector in RGB-color scale. This view forms the basis for the formal description of operations with distributions using the analytical apparatus of the "color" of the algebra.
Keywords: algebra of distributions, measurement form, RGB-scale, comparison of the signals, the color model.
ВВЕДЕНИЕ
Эффективное решение задач обработки сложных сигналов в радиотехнике предполагает наличие некоторой априорной информации, определяющей выбор алгоритмов и инструментов для дальнейшего анализа выборочных реализаций исследуемого сигнала. Для пользователя наиболее важной является та априорная информация, которая дает правильный (адекватный) ответ на вопрос: «Что это за сигнал?». Соответственно этому, строится аналитическая или алгоритмическая модель входного сигнала, производится измерение характеристик и параметров модели и оценка результатов анализа на предмет их «коррелированности» физическому смыслу задачи.
В случае отсутствия подобной, априорной информации, модель сигнала формируется путем его структурной или/и параметрической идентификации [1] с некоторым заранее выбранным набором, так называемых, «эталонных» моделей. При этом предполагается, что выборочная реализация сигнала обладает информационной избыточностью, в соответствие с которой вся информация о сигнале заключена в его форме.
Обобщенное представление моделей сигналов в пространстве временных функций рассмотрено в работе [2]. Некоторые возможности идентификации моделей сложных сигналов в спектральной области описаны в статье [3]. Относительно хорошо изученными в настоящее время являются те модели [4,5], которые ориентированы на представление формы распределения мгновенных значений сигналов в виде особых, идентификационных чисел (параметров). Инструменты, осуществляющие преобразование выборочных реализаций сигнала в идентификационные числа, получили название идентификационных тестеров (ИТ). Вопросы, связанные с построением ИТ и их использованием наиболее полно изложены в монографиях [6-8].
Анализ и обобщение полученных результатов позволяют сформулировать проблему следующего этапа исследований: разработка аналитического аппарата, предназначенного для описания эффектов взаимодействия и преобразования формы распределений. Подобный аппарат, назовем его алгеброй распределений, должен быть ориентирован на решение задач суммирования, вычитания, умножения и деления распределений, представленных своими идентификационными числами. В этом случае появляется реальная возможность расчетным путем прогнозировать результаты взаимодействия сложных сигналов. В данной статье рассмотрены свойства одной из моделей идентификационных тестеров с точки зрения формирования на ее основе элементов алгебры распределений.
МЕТОДИКА И ИНСТРУМЕНТЫ ИССЛЕДОВАНИЯ
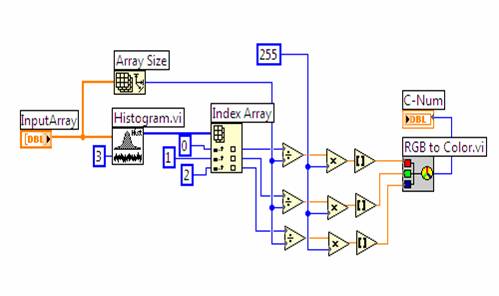
Предлагаемая «цветовая» модель формы распределений использует идею, изложенную в работе [9], и является дальнейшим ее развитием. Суть модели поясняется структурной схемой (рис. 1) программного кода виртуального прибора (C-tester.vi), выполненного в среде графического программирования LabVIEW-7.1.
Рис. 1. «Цветовая» модель формы распределений.
Принцип действия модели основан на представлении выборки исследуемого сигнала (InputArray) в виде гистограммы (Histogram.vi) распределения, содержащей всего три моды, подобно тому, как это делается при измерении цвета некоторого объекта с помощью векторной RedGreenBlue-шкалы. RGB-моды гистограммы нормируются относительно объема N выборки (Array Size.vi) и умножаются на постоянный коэффициент, равный 255, для того, чтобы обеспечить правильную работу синтезатора цвета (RGB to Color.vi). На выходе этого инструмента формируется число (C-Num), являющееся цветовым кодом входного анализируемого распределения. В данном случае три моды гистограммы выступают в качестве весовых коэффициентов α, β, γ цветовых векторов R, G, B в уравнении
![]() .
(1)
.
(1)
Таблица 1
Результаты экспериментов с «цветовой» моделью распределений
|
№ п/п |
Имя распределения |
Компоненты цветового вектора |
Цвет |
Примечание |
||
|
R |
G |
B |
||||
|
1 |
2mod |
128 |
0 |
127 |
|
|
|
2 |
asin |
100 |
55 |
100 |
|
|
|
3 |
even |
85 |
85 |
85 |
|
|
|
4 |
trap |
73 |
109 |
73 |
|
|
|
5 |
simp |
59 |
137 |
59 |
|
|
|
6 |
gaus |
37 |
181 |
37 |
|
|
|
7 |
lapl |
19 |
217 |
19 |
|
|
|
8 |
Kosh (без усреднения C-Num) |
0 |
254 |
1 |
|
|
|
9 |
Kosh (с усреднениемC-Num) |
82 |
93 |
80 |
|
|
|
10 |
expn |
231 |
21 |
2 |
|
|
|
11 |
rele |
146 |
99 |
10 |
|
|
|
12 |
poison |
190 |
60 |
5 |
|
|
|
13 |
Gamma-2 |
213 |
39 |
3 |
|
|
|
14 |
binomial |
64 |
127 |
64 |
|
|
|
15 |
Bern-0,8 |
51 |
0 |
204 |
|
|
|
16 |
Bern-0,2 |
203 |
0 |
52 |
|
|
При изменении формы распределения изменяются весовые коэффициенты мод, цветовой код на выходе синтезатора цвета и, соответственно, цвет. Для индикации цвета распределения на выход синтезатора цвета необходимо подключить индикатор типа Color Box.
Адекватность работы модели была проверена на тестовых периодических (squ, sin, tri) и случайных (2mod, asin, even, trap, simp, gaus, lapl, kosh) сигналах и проиллюстрирована на рис. 2 – 6. Результаты экспериментов сведены в табл. 1.
Анализ представленных результатов позволяет сделать следующие выводы.
Во-первых, подтверждается существование аналогии (как по цвету – Color Box, так и по значению цветового кода C-Num) периодических сигналов прямоугольной (squ), синусоидальной (sin) и треугольной (tri) формы и соответствующих случайных сигналов с двумодальным (2mod), арксинусным (asin) и равномерным (even) распределениями. Эту аналогию можно распространить на любые сигналы и, тем самым, устанавливать соответствие классов регулярных и хаотических сигналов.
Во-вторых, поскольку палитра RGB-шкалы включает миллионы цветов, то «цветовая» модель оказывается весьма чувствительна к изменениям формы гистограммы, особенно в отношении перераспределения интенсивности мод.
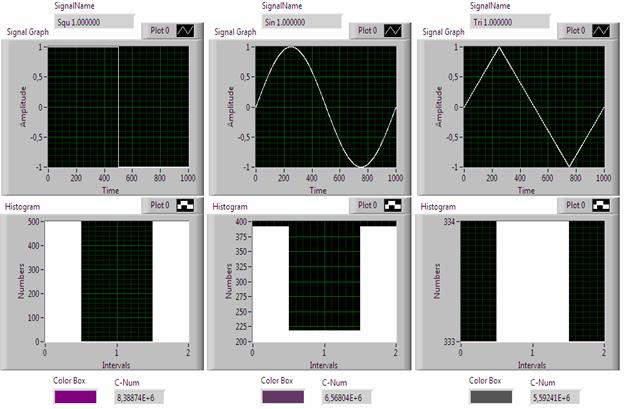
Рис. 2. Иллюстрации работы «цветовой» модели с периодическими сигналами прямоугольной (squ-1), синусоидальной (sin-1) и треугольной (tri-1) формы.
В-третьих, «цветовая» модель способна идентифицировать такие свойства, как симметрия, выпуклость (вогнутость) и скошенность распределений. Например, показанные на рис. 6 три распределения типа Коши, отличаются расположением моды (максимума) либо в первой (R), либо во второй (G), либо в третьей (B) компонентах цветового вектора. Цвета этих распределений изменяются от красного (левая колонка) до голубого (правая колонка, рис. 6), соответственно. При этом центральному расположению моды гистограммы соответствует зеленый цвет.

Рис. 3. Иллюстрации работы «цветовой» модели со случайными сигналами (2mod, asin, even – распределения).
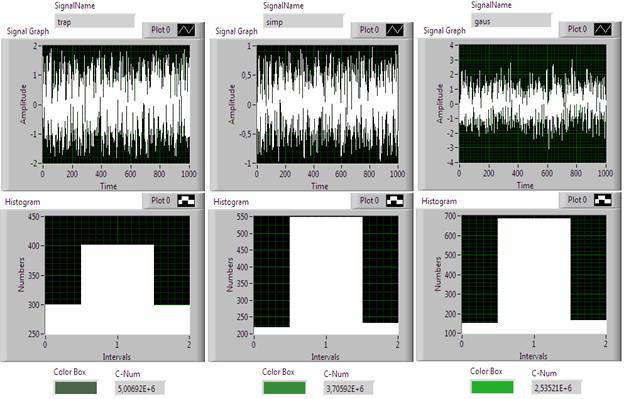
Рис. 4. Иллюстрации работы «цветовой» модели со случайными сигналами (trap, simp, gaus – распределения).
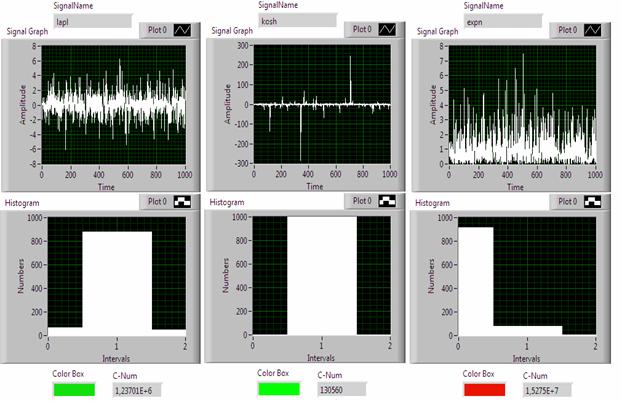
Рис. 5. Иллюстрации работы «цветовой» модели со случайными сигналами (laplkoshexpn – распределения).
Рис. 6. Иллюстрации работы «цветовой» модели со случайными сигналами типа kosh – распределения, но разной симметрии.
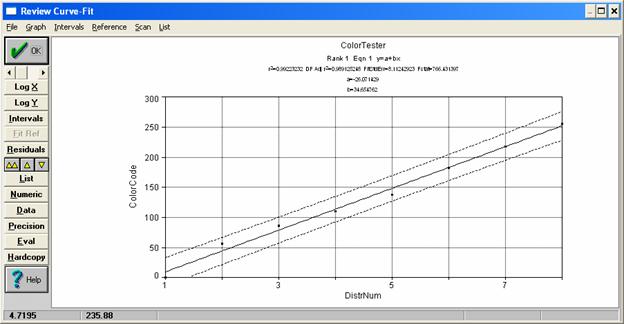
В-четвертых, наблюдается линейная корреляция между цветовым кодом и именами симметричных распределений случайных сигналов (рис. 7) для G-моды, поскольку остальные моды (R&G) равны между собой.
Указанная аналитическая зависимость получена программой TCWin (фирма Jandel Scientific) в режиме подбора по 4000 моделям собственной БД с использованием критерия минимума среднеквадратического отклонения. Ранг модели (Rank=1) указывает на то, что данная зависимость (рис. 7) является наилучшей в классе простейших моделей. Полученную зависимость можно использовать для решения задачи интерполяции положения неизвестного распределения на RGB-шкале. Для этого, по измеренному значению весового коэффициента путем обратного решения уравнения оценивается порядковый номер, который, в общем случае, может быть рациональным, а не целым, числом.
Рис. 7. Аналитическая модель цветовой шкалы для G-модs симметричных распределений.
Поскольку стандартный размер RGB-шкалы составляет 256 (28) градаций (рис. 7), а размер цветового кода (C-Num) на выходе тестера (рис.1) достигает (в максимуме) значений 1,67117Е+7, то можно подсчитать максимальное количество (Lmax = (C-Num)/255 = 65536 или 216) RGB-шкал, укладывающихся в размере цветового кода. Введение параметра (L) вызвана необходимостью различать такие распределения, которые имеют одинаковые цвета, расположенные на разных интервалах периодичности.
Аналогом данного свойства цветовой модели является интерференционная картина, число полос которой определяет количество периодов сигнала, прошедших через данную точку плоскости наблюдения. В промежутке между темными (светлыми) полосами интенсивность интерференции изменяется по закону cos2(φ/2), где φ – сдвиг фаз между взаимодействующими векторами сигналов. Принцип счета числа полос интерференции достаточно широко используется в различных оптико-электронных приборах, предназначенных, например, для измерения малых перемещений [10]. В подобных приборах измеряется также «дробная» часть периода, определяющая конечное положение фотоприемника между интерференционными полосами. Сочетание счета и интерполяции внутри кванта интерференции позволяет достичь высокой точности измерения в широком диапазоне перемещений.
Другим примером устройств, которые используют периодичность статической характеристики, могут служить, так называемые, «сверточные» АЦП [11], сочетающие в себе высокое быстродействие и разрешающую способность.
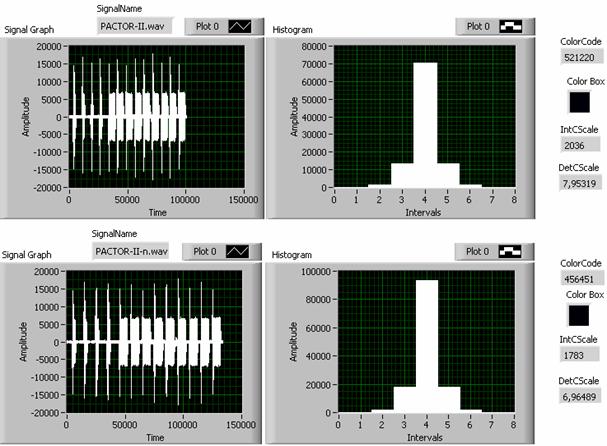
Рис. 8. Пример сравнения похожих по структуре сложных сигналов.
Способность цветовой модели различать визуально похожие сигналы проиллюстрирована на рис. 8, на котором, кроме временных функций и гистограмм представлены количественные оценки идентификационных параметров: 1) значения цветового кода (ColorCode); 2) целое число периодов (IntCScale) RGB-шкалы, укладывающихся в цветовом коде; 3) дробная часть периода (DetCScale) RGB-шкалы. Используя эти параметры можно сформировать оценку степени различия, например, в виде относительного отклонения: δ = (ColorCode1 – ColorCode2)/ (ColorCode1 + ColorCode2).
Линейный характер модели (рис.7) позволяет предположить, что в рамках RGB-шкалы можно установить (по аналогии) алгебру распределений. Это, в свою очередь, позволит аналитически рассчитывать результаты взаимодействия сигналов. По-видимому, операции с векторами в RGB-шкале будут отличаться от подобных же операций в обычной векторной алгебре и, вполне возможно, будут похожи на операции с цветовыми векторами.
Перспективы использования «цветовой» шкалы распределений связаны с построением интеллектуальных систем обработки данных, решающих задачи идентификации и распознавания (сравнения) сигналов.
Литература
1. Штейнберг Ш.Е. Идентификация в системах управления. – М.: Энергоатомиздат, 1987. - 80 с.
2. Горшенков А.А. Кликушин Ю.Н. Представление моделей сигналов в системе идентификационных параметров [Электронный ресурс]. // Журнал радиоэлектроники. – 2010. – N9. – Режим доступа: http://jre.cplire.ru/jre/sep10/3/text.html, свободный. – Загл. с экрана.
3. Горшенков А.А. Кликушин Ю.Н. Некоторые закономерности идентификационных измерений спектров сигналов [Электронный ресурс]. // Журнал радиоэлектроники. – 2011. – N2. – Режим доступа: http://jre.cplire.ru/jre/feb11/1/text.html, свободный. – Загл. с экрана.
4. Кликушин Ю.Н.Классификационные шкалы для распределений вероятности [Электронный ресурс]. // Журнал радиоэлектроники. – 2000. – N11. – Режим доступа: http://jre.cplire.ru/jre/nov00/4/text.html, свободный. – Загл. с экрана.
5. Кликушин Ю.Н. Библиотека виртуальных инструментов анализа и синтеза формы сигналов // Свидетельство о госрегистрации, №50200601945, Министерство образования и науки РФ, ОФАП, М.: 2006.
6. Кликушин Ю.Н. Технологии идентификационных шкал в задаче распознвания сигналов: Монография. - Омск: Изд-во ОмГТУ, 2006 - 96 с.
7. Кликушин Ю.Н., Кошеков К.Т. Методы и средства идентификационных измерений сигналов: Монография. – Петропавловск: Изд-во СКГУ им. М. Козыбаева, 2007. – 186 с.
8. Кликушин Ю.Н. Идентификационные инструменты анализа и синтеза формы сигналов: Монография. - Омск: Изд-во ОмГТУ, 2010. - 216 с.
9. Кликушин Ю.Н. RGB-шкала для измерения распределений [Электронный ресурс]. // Журнал радиоэлектроники. – 2008. – N3. – Режим доступа: http://jre.cplire.ru/jre/mar08/3/text.html, свободный. – Загл. с экрана.
10. Фотоэлектрические преобразователи информации/Под ред.Л.Н.Преснухина. - М.: Высш. шк., 1970.
11. Интернет-ресурс (сайт) - http://radioteh.info/category/pribori-dlya-izmyeryeniya-paramyetrov-radiosignalov/page/5/