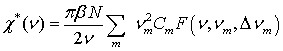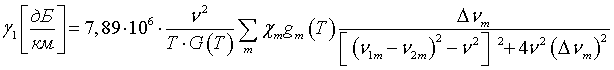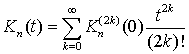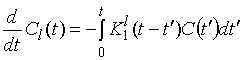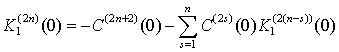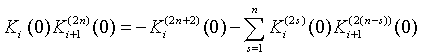УДК: 535.34-14
МОЛЕКУЛЯРНОЕ ПОГЛОЩЕНИЕ В АТМОСФЕРНЫХ ПАРАХ ВОДЫ В 0-1Тгц ЧАСТОТНОМ ДИАПАЗОНЕ
А. Ю. Зражевский, С. В. Титов
Институт радиотехники и электроники им. В.А. Котельникова РАН, Фрязинский филиал
Получена 1 октября 2012 г.
Аннотация. Разработана простая методика инженерного описания ослабления в атмосферном водяном паре. Описан также единый теоретический подход к расчету широкополосных спектров дисперсии и поглощения полярных газов. Он основан на формализме функций памяти. Теория применена для расчета ослабления в атмосферном водяном паре.
Ключевые слова: молекулярное поглощение, водяной пар, метод функций памяти.
Abstract. Engineering method for the evaluation of an absorption in atmospheric water vapour is proposed. Theoretical approach for the description of broad band spectra of dispersion and absorption of polar gases is also presented. This approach is based on the memory function formalism. The theory is applied for the calculation of the absorption in atmospheric water vapour.
Key words: molecular absorption, water vapor, memory function approach.
Введение
Совершенствующаяся техника связи и дистанционного зондирования обуславливает необходимость знания полной и точной спектроскопической информации о газах для интерпретации дистанционных измерений, оценок ослабления излучения, моделирования радиационного переноса и т.п. В последние годы повысился интерес к исследованиям особенностей распространения миллиметровых и субмиллиметровых радиоволн в атмосфере, что связано с рядом новых применений их при изучении космического пространства, природных ресурсов Земли, в локации, связи и спутниковой навигации. Земная атмосфера достаточно хорошо изучена [1]. Она состоит из смеси газов, гидрометеоров и аэрозолей, которые в свою очередь сильно влияют на характер распространения электромагнитных волн, меняя их интенсивность, направление и дальность распространения, внося дополнительные помехи.
Ослабление электромагнитных волн в атмосфере при отсутствии гидрометеоров и аэрозолей практически полностью определяется молекулярным поглощением, которое принято рассчитывать на основе квантово-механической теории [2]. Из множества образующих атмосферу газов способностью существенно поглощать энергию электромагнитных волн, переводя ее в тепловую энергию и рассеивая в атмосфере, обладают в основном кислород и водяной пар. Это связано с тем, что молекулы воды и кислорода имеют электрический и магнитный дипольные моменты, соответственно, которые взаимодействуют с электромагнитной волной. Ослабление в примесных газах атмосферы Оз, СО, N2O и др., молекулы которых тоже обладают дипольными моментами, значительно меньше из-за их малых концентраций. В данной работе рассматривается поглощение только в водяном паре. Поглощение в кислороде описано, например, в работе [3].
Теоретический спектр поглощения паров воды можно рассчитать, выполняя суммирование по отдельным квантово-механическим вращательным переходам, обуславливающим резонансные линии в спектре поглощения. В качестве формы линии обычно используются известные линии Лорентца, Ван Флека-Вайскопфа или Гросса [4,5]. Модель (линия) Гросса известна также в спектроскопии полярных жидкостей, как M-диффузия, а в спектроскопии газов, как линия, получаемая из решения кинетического уравнения (КУ) [2]. Такой расчет показывает хорошее соответствие теории и эксперимента в резонансных областях вращательного спектра поглощения паров воды, однако в окнах атмосферной прозрачности для радиоволн на частотах 0 < n < 30 см-1 (0 ¸ 1 ТГц) экспериментальные значения в 1,5-2 раза превышают соответствующие теоретические величины [5,6]. Попытки объяснить это несоответствие с помощью привлечения гипотез о дополнительных механизмах поглощения димерами (Н2О)2 [7] и поглощения, индуцированного при соударениях молекул Н2О-N2О, Н2О-O2, Н2О-H2О [8,9], привели к противоречивым результатам [10,11].
На основании экспериментальных и теоретических исследований [12-20] была высказана гипотеза о том, что неточность расчётных величин коэффициента поглощения вызвана неадекватностью обычно применяемых форм-факторов спектральных линий в области их крыльев. Например, обычно применяемые форм-факторы линий не объясняют:
- различное превышение экспериментально полученных значений над расчётными величинами для поглощения в разных газовых смесях водяного пара [10,11,17],
- изменение значения параметра уширения линии при переходе от линий поглощения к окнам прозрачности атмосферы,
- увеличенную нелинейность в зависимости поглощения от влажности воздуха в окнах прозрачности.
В мировой литературе периодически уделяется внимание вопросам теоретического описания крыльев спектральных линий газов [11,21,22], однако удобный метод моделирования аналитической формы линии, пригодной для широкого диапазона частот, до сих пор не предложен. До сих пор ведутся работы по усовершенствованию квантово-механической теории для приведения ее в соответствие с экспериментами по поглощению в газах. Продолжается также развитие полуэмпирических методов расчета коэффициентов поглощения газовых смесей.
Методика инженерного расчета поглощения в атмосферных парах воды
Квантово-механические расчеты
спектров газов с использованием форм-факторов спектральных линий осуществляются
следующим образом. Комплексная восприимчивость газа ![]() выражается
в виде суммы по отдельным линиям [2]
выражается
в виде суммы по отдельным линиям [2]
где ![]() - амплитуда линии,
- амплитуда линии, ![]() комплексный форм-фактор линии, m – номер линии, b=(kБT)-1, T – температура, kБ – постоянная Больцмана, N – концентрация дипольных молекул. Коэффициент
поглощения выражается через мнимую часть восприимчивости как [2]
комплексный форм-фактор линии, m – номер линии, b=(kБT)-1, T – температура, kБ – постоянная Больцмана, N – концентрация дипольных молекул. Коэффициент
поглощения выражается через мнимую часть восприимчивости как [2]
![]() (2)
(2)
Привести расчетные значения в согласие с экспериментом можно, например, используя следующий фактор-формы [18]
Контур при Z = 2 переходит в форм-фактор
Гросса (КУ). Основным отличием этого контура от традиционно используемых
является наличие не одного параметра, а двух: полуширины линии и параметра Z. Аналогичная идея двух параметров в
факторе-формы позже была применена, например, Розенкранцем [23]. В линии
Розенкранца параметрами являются полуширина ![]() и
интерференционный коэффициент
и
интерференционный коэффициент ![]() , характеризующий
влияние всех других линий на форму данной линии (интерференционный эффект).
Именно линия Розенкранца лежит в основе инженерных программ расчета
атмосферного ослабления MPM2
[24].
, характеризующий
влияние всех других линий на форму данной линии (интерференционный эффект).
Именно линия Розенкранца лежит в основе инженерных программ расчета
атмосферного ослабления MPM2
[24].
При Z<2 низкочастотное крыло линии (3) приподнято, а высокочастотное – опущено по сравнению с крыльями линии Гросса (КУ) (см. рис. 1 и 2). На рис. 1 показаны оба контура: линия Гросса (КУ) и линия . Видно, что различие между ними наблюдается только в крыльях и что оно невелико. Вблизи линии, где ν ~ νm контур совпадает с контуром линии Гросса (КУ).

Рис.1 Контуры линий Гросса (штриховая) и (сплошная).
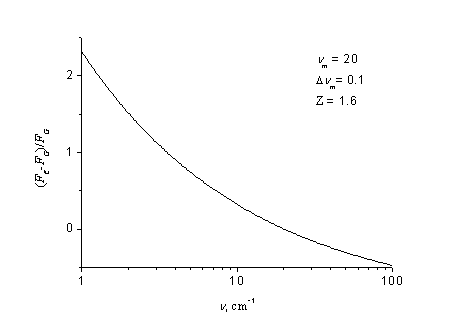
Рис.2 Отличие формы линии, приводящей в согласие расчет с экспериментом, от линии Гросса (КУ).
Значение Z определено по критерию максимального согласия с экспериментальными данными в атмосферных парах воды при нормальных условиях и равно 1,6 [18]. При Z=1,6 в ММ и СбММ диапазонах было получено совпадение с экспериментальными данными, то есть именно там, где с форм-фактором линии Гросса (КУ) его получить не удавалось. При этом на частотах: 5; 6; 7; 7,5; 8; 9; 10; 10,88; 11; 11,25; 13,75; 22,25; 28,5; 31; 34 см-1 для нормальных условий (S0=0,01, Р0=760 мм рт. ст., Т0= 293 К, здесь S – относительная объемная концентрация водяного пара, этим условиям соответствует абсолютная влажность воздуха 7,5 г/м3) были получены значения коэффициентов поглощения: 1,35; 13,2; 2,54; 2,63; 2,92; 3,78; 5,27; 38,3; 20,2; 9,92; 17,6;48,5; 51,8; 101; 271 дБ/км соответственно. В высокочастотном крыле вращательного спектра водяного пара (в ИК диапазоне) были вычислены коэффициенты поглощения на длине волны 10,6 мкм с форм-фактором линий Гросса (КУ) и по формуле ; они равны соответственно 0,76 и 0,38 дБ/км. В измерениях были получены величины 0,32 и 0,35 ±0,07 дБ/км. Таким образом, и в высокочастотной части спектра контур приводит в согласие теорию с опытом. Однако на частотах 1, 2, 3, 4 см-1 с помощью линии были получены коэффициенты поглощения 0,104; 0,254; 0,467; 0,825 дБ/км, которые в 1,3 – 1,7 раза больше опытных данных.
Рассмотренный пример позволяет сделать вывод о том, что возможна модификация форм-фактора спектральной линии, которая приводит к согласию расчёт и эксперимент в ММ, длинноволновой части СбММ и ИК диапазонах и не нарушает специальных требований, предъявляемых к контуру спектральной линии. Этот пример показывает главное, что, изменяя форму линии в области крыльев, можно обеспечить согласие со всеми известными экспериментальными данными в ММ и СбММ диапазонах волн. Откуда следует, что основная причина расхождения теории молекулярного поглощения в парах воды с экспериментом может быть объяснена некорректным описанием форм-фактора линии.
Для длин волн, больших 0,28 мм, нами была разработана методика инженерного расчёта поглощения [25], имеющая целью обеспечить максимальное согласие с экспериментом при значительном упрощении процесса вычислений. Она основана на предположениях, как об отличии реальной формы спектральной линии в области крыльев от линии Гросса (КУ), так и на том, что квантово-механические соотношения с формой линии Гросса (КУ) качественно верно отражают зависимости поглощения от метеопараметров и частоты. Последнее следует из сравнения с результатами измерения поглощения как функции влажности [13,14,19], давления [12] и температуры [20] воздуха и подтверждается экспериментами с другими газовыми смесями водяного пара в СбММ диапазоне [17,26].
Ослабление в парах воды в [25] представлено в виде суммы: γ1 – поглощения от линий, частоты переходов которых находятся в спектральном интервале 0-36,6 см-1 и γ2 - поглощения от всех остальных линий, резонансные частоты которых удалены от этого участка. В величине γ2 учтено также ожидаемое отличие реального контура линии от расчетного для всех линий вращательного спектра водяного пара с J ≤ 10.
Здесь m – порядковый номер линии; G(Т) – статистическая сумма: G(Т)=3,397.10-2Т3/2,
![]() – функция населённости; b = 1,4388;
– функция населённости; b = 1,4388; ![]() –
энергии уровней; ∆νm – полуширины спектральных линий в
воздухе, которые определяются через парциальные полуширины
–
энергии уровней; ∆νm – полуширины спектральных линий в
воздухе, которые определяются через парциальные полуширины ![]() , вычисленные по формуле [27]:
, вычисленные по формуле [27]:
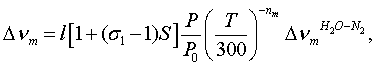 (5)
(5)
где l- коэффициент, полученный по критерию максимального
согласия с экспериментом (в среднем для всех измеренных линий l =1,02-1,03), nm – температурный коэффициент
полуширины, взятый по [27], σ1 –параметр самоуширения
(в среднем близок к 5 [28]). В величине ![]() учтены:
квадраты матричных элементов дипольного момента по модели жёсткого волчка,
статистические веса уровней и резонансные частоты переходов. Коэффициент
7,89·106 получен при значении дипольного момента µ0=1,884·10-18СGSE. Значения величин ν1m, ν2m,
учтены:
квадраты матричных элементов дипольного момента по модели жёсткого волчка,
статистические веса уровней и резонансные частоты переходов. Коэффициент
7,89·106 получен при значении дипольного момента µ0=1,884·10-18СGSE. Значения величин ν1m, ν2m, ![]() , nm и
, nm и ![]() приведены в [18].
приведены в [18].
С учетом известных экспериментальных данных и сопоставления их с расчетными зависимостями от частоты и метеопараметров получено выражение для γ2:
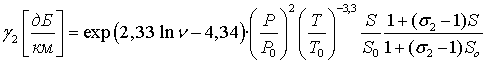 (6)
(6)
По данным обзора экспериментальных данных [18] для частот ν = 1; 2; 3; 4; 5; 7; 8; 9; 10; 11.2; 13.7; 22.2; 28.5; 31 и 34 см-1 были получены усредненные значения γэо =0.05; 0.12; 0.3; 0.56; 0.95; 2.5; 2.9; 3.9; 5.1; 10.5; 19; 60; 60; 100 и 250 дБ/км, соответственно, при значениях σ1=5, σ2 =14 и l=1,025.
Для окон прозрачности СбММ диапазона с центрами на λ= 0.87 (11.5); 0.73 (13.7); 0.45 (22.2) 0.36 (27.7) и 0.29 мм (34.5см-1) были получены соответственно величины γ=10.3; 18.9; 57.6; 67.7; 238 дБ/км, которые близки к средним значениям многих измерений.
На частотах переходов спектральных линий с νm= 6,12; 10,88; 12,67 и 25,10 получены значения 2.88х101, 3.94х101, 3.02х102 , 1.14х104 дБ/км соответственно, которые практически совпадают с экспериментальными данными.
Вид зависимостей поглощения от давления и влажности согласуется с видом, следующим из расчёта по полной квантово-механической формуле, причём дополнительно учитывается также и наблюдаемое в экспериментах отличие в величинах параметра самоуширения на разных расстояниях от частот переходов. Полученные нами результаты на λ=0,45 мм показывают согласие видов расчётной и измеренной зависимостей γ от Т. Методика инженерного расчёта обеспечивает близкое совпадение характера изменения поглощения от температуры с вычисленными по полной квантово-механической формуле. Например, в диапазоне температур 213 – 313 К на длинах волн 10≥λ≥0,28мм величины( γT /γ0 ), рассчитанные по методу инженерного расчёта и по квантово – механической формуле, согласуются с точностью ~5% . Это иллюстрирует рис. 3, на котором для окон прозрачности СбММ диапазона нанесены зависимости поглощения от температуры, вычисленные этими двумя способами.
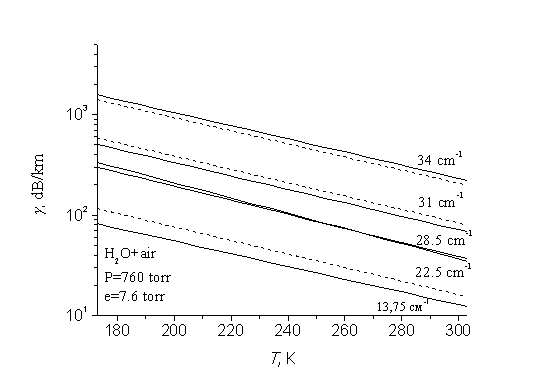
Рис.3 Расчетные зависимости коэффициентов поглощения в воздухе от температуры в окнах прозрачности с центрами на длинах волн 13.75, 22.25, 28.5, 31 и 34 см-1. Штриховые линии - квантово-механическая формула, сплошные линии - методика инженерного расчета.
В расчетах использовались линии с J≤10. Во многих случаях можно вводить в расчёт только 17 основных линий, опуская остальные. Значение γ2 при этом остаётся прежним. Разница в величинах поглощения на частотах перехода опущенных линий при расчётах с 17 и 23 линиями при нормальных условиях составляет не более 7%.
Спектральный интервал, на
котором возможен расчет по предлагаемой методике, с одной стороны, ограничен
длиной волны λ![]() 0,28 мм. С другой
стороны, границу трудно указать, так как при λ≥10-20 мм точность экспериментальных данных недостаточна для того чтобы судить о степени соответствия им
расчётных величин, но и на этих длинах волн экспериментальные точки хорошо
ложатся на расчётную кривую γ=f(ν).
0,28 мм. С другой
стороны, границу трудно указать, так как при λ≥10-20 мм точность экспериментальных данных недостаточна для того чтобы судить о степени соответствия им
расчётных величин, но и на этих длинах волн экспериментальные точки хорошо
ложатся на расчётную кривую γ=f(ν).
Вопрос о показателе преломления атмосферных паров воды и его зависимости от параметров атмосферы обсуждался в работе [38]. В окнах прозрачности показатель преломления определяется крыльями линий. Этот факт может служить для точного определения форм-фактора в нерезонансной части. Это особенно существенно, поскольку современная техника позволяет измерять показатель преломления с достаточно хорошей точностью. Отмечено хорошее согласие экспериментальных данных [38] по измерению показателя преломления с расчетами по методике работы [25].
В монографии [37] приведены результаты многолетних измерений радиояркостной температуры на входе приемного устройства, обусловленной нисходящим излучением атмосферы в ММ и СбММ диапазонах в горных условиях. Было показано, что нежесткость молекул и вклад слабых линий практически не влияет на суммарное поглощение в атмосфере. Соответствие результатов расчета с экспериментальными данными достигается в основном за счет уточнения формы спектральной линии. Отмечено хорошее согласие экспериментальных данных с расчетными зависимостями поглощения от угла наблюдения, высоты над уровнем моря, атмосферными условиями. При этом за основу расчетов бралась методика работы [25].
Механизмы теплового вращения молекул и диэлектрические параметры полярных газов: метод функций памяти
Задача вычисления молекулярного поглощения связана с исследованием динамики молекул в газах. Такая связь объясняется тем, что расчеты макроскопических характеристик (например, комплексной диэлектрической восприимчивости) основываются на микроскопическом рассмотрении динамических процессов в газах. Недавно полученное нами [2,29] обобщение метода функций памяти на квантовый случай позволило с единых позиций исследовать механизмы теплового вращения молекул и влияния различных факторов (времен соударений молекул, интерференции линий и др.) на диэлектрические параметры полярных газов в миллиметровом (ММ) и субмиллиметровом (СбММ) диапазонах длин волн. В частности, показана эффективность метода в описании спектров поглощения водяного пара, основанная на учете влияния длительности соударений молекул на диэлектрические характеристики водяного пара в диапазоне частот до 1 ТГц. Исследование проявления интерференционных эффектов во вращательных спектрах поглощения полярных газов в ММ и СбММ диапазонах длин волн позволило разработать современную методику описания спектра поглощения молекулярного кислорода [3].
Преимущество метода функций памяти по сравнению с традиционными методами (кинетического уравнения, автокорреляционных функций) в том, что в нем рассматриваются не сами корреляции динамических переменных, а их производные n-го порядка, что во многих случаях упрощает задачу. Кроме того, метод позволяет судить об асимптотических свойствах спектров без громоздких вычислений. Метод функций памяти широко используется в неравновесной статистической термодинамике. В последнее время этот метод все большее применение находит и в теории диэлектрической спектроскопии [2].
Расчеты
диэлектрических характеристик основаны на соотношениях, связывающих комплексную
восприимчивость ![]() , спектр автокоррелляционной
функции дипольного момента
, спектр автокоррелляционной
функции дипольного момента ![]() и спектр функции
памяти
и спектр функции
памяти ![]() (
(![]() )
)
![]() (7)
(7)
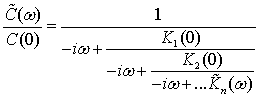 (8)
(8)
где символ «» означает одностороннее преобразование Фурье.
Для того чтобы рассчитать спектр комплексной диэлектрической проницаемости газа в ММ и СбММ диапазонах длин волн, необходимо основываться на определенных представлениях о вращении молекул в этой среде с учетом их взаимодействия с окружением. Молекулярное вращение часто рассматривается в рамках модели обобщенной вращательной диффузии [2]. Термин "обобщенная" свидетельствует о расширенном (обобщенном) толковании диффузионного процесса, когда возможно свободное (инерционное) вращение молекулы между столкновениями, а столкновения могут считаться как "слабыми", так и "сильными". Различные упрощения, используемые для получения расчетных выражений для диэлектрических характеристик, приводят к понятию моделей обобщенной вращательной диффузии. К ним относятся модели Лорентца, Ван Флека-Вайскопфа, М- и J-диффузии, Блио-Конста, Бхатнагара-Гросса-Крука (БГК) и ряд других, успешно использовавшихся для описания ММ и СбММ спектров молекулярного поглощения и дисперсии полярных газов и жидкостей [2].
Для теоретического описания молекулярного поглощения в газах и жидкостях нами использовалась модель J-диффузии [2,29]. В этой модели предполагается, что свободное вращение молекулы прерывается «мгновенными» неадиабатическими столкновениями (средняя длительность столкновений td много меньше среднего времени между столкновениями tc ) и изменяется как величина, так и направление вектора углового момента молекулы J. Область применимости первоначальной версии модели J-диффузии ограничивалась допущением о мгновенности столкновений молекул, что соответствует выполнению условий td << tc и 2pсtd << n-1. Однако первое условие не выполняется для сжатых газов. Второе неравенство нарушается в субмиллиметровой области даже в случае газов при нормальных условиях, так как (2pсtd)-1 порядка v/d ~ 10-12-10-13 сек (d - диаметр молекулы и v - ее средняя поступательная скорость), что соответствует частотам СбММ диапазона. В работах [2,3,29-31] указанные ограничения были устранены и модель J-диффузии обобщена на случай, когда длительность столкновений молекул имеет конечную величину, при этом молекулы могут быть произвольной симметрии.
Было проведено детальное сопоставление теории с экспериментальными данными по широкополосным спектрам молекулярного кислорода и водяного пара [2,3,29-31]. Столкновительное уширение учитывалось в рамках квантово-механической модели J-диффузии.
Для описания вращательного спектра паров воды в качестве модельной функции памяти в [2] предлагалось использовать следующее выражение:
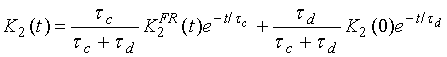 (9)
(9)
где ![]() -
функция памяти второго порядка модели свободного вращения, tc и td - времена релаксации.
-
функция памяти второго порядка модели свободного вращения, tc и td - времена релаксации.
Выбор модельной функции
памяти K2(t)
определяется следующими ее свойствами. Модель учитывает (в первом приближении)
основные молекулярно-динамические процессы в газах: почти свободное вращение
между столкновениями и сам процесс столкновений. Вращение молекул описывается
функцией памяти Блио-Конста ![]() . В модели
предполагается, что молекулы совершают свободное вращение, прерываемое
случайными столкновениями. После столкновения величина момента количества
движения и проекция его на выделенную ось лабораторной системы координат
приобретают новое значение с вероятностью, пропорциональной максвелловскому
распределению. При этом ориентация молекулы остается неизменной. Предполагается
также конечность среднего момента сил, действующих на молекулу [2]. Процесс
взаимодействия (столкновения) моделируется функцией памяти
. В модели
предполагается, что молекулы совершают свободное вращение, прерываемое
случайными столкновениями. После столкновения величина момента количества
движения и проекция его на выделенную ось лабораторной системы координат
приобретают новое значение с вероятностью, пропорциональной максвелловскому
распределению. При этом ориентация молекулы остается неизменной. Предполагается
также конечность среднего момента сил, действующих на молекулу [2]. Процесс
взаимодействия (столкновения) моделируется функцией памяти ![]() . Характерное время релаксации этого
процесса td. По физическому смыслу время td можно уподобить времени, в течение
которого происходит столкновение. Раньше в квантово-механических расчетах это
время не учитывалось. Форм-фактор линии задавался либо одним параметром (полушириной,
зависящей только от времени между соударениями), либо двумя – полушириной и
интерференционными коэффициентами, как в линии Розенкранца. Из вышесказанного
также следует, что введение времени соударения может быть вполне теоретически обосновано,
а следовательно и приводить в согласие теорию с экспериментом. Представление
функции памяти в виде суммы двух функций можно интерпретировать как наличие
двух молекулярных процессов.
. Характерное время релаксации этого
процесса td. По физическому смыслу время td можно уподобить времени, в течение
которого происходит столкновение. Раньше в квантово-механических расчетах это
время не учитывалось. Форм-фактор линии задавался либо одним параметром (полушириной,
зависящей только от времени между соударениями), либо двумя – полушириной и
интерференционными коэффициентами, как в линии Розенкранца. Из вышесказанного
также следует, что введение времени соударения может быть вполне теоретически обосновано,
а следовательно и приводить в согласие теорию с экспериментом. Представление
функции памяти в виде суммы двух функций можно интерпретировать как наличие
двух молекулярных процессов.
Мнимая часть комплексной
диэлектрической восприимчивости ![]() , рассчитанная на
основе данной модельной функции памяти, удовлетворяет правилам сумм [2]
, рассчитанная на
основе данной модельной функции памяти, удовлетворяет правилам сумм [2]
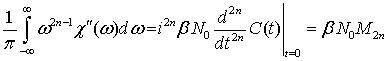 , n=0,1,2,…
(10)
, n=0,1,2,…
(10)
Здесь ![]() - спектральные моменты. Следует заметить, что в модели Ван
Флека-Вайскопфа правило сумм удовлетворяется только для n = 0, а в
модели Лорентца - для n = 1.
- спектральные моменты. Следует заметить, что в модели Ван
Флека-Вайскопфа правило сумм удовлетворяется только для n = 0, а в
модели Лорентца - для n = 1.
В рамках данной модели выражение для восприимчивости сводится к сравнительно простому виду
где
![]()
![]() (12)
(12)
![]() и
и ![]() - значения функций памяти модели
свободного вращения первого и второго порядков при t = 0,
- значения функций памяти модели
свободного вращения первого и второго порядков при t = 0, ![]() - амплитуды линий. Необходимые при
расчетах спектров константы можно рассчитать непосредственно, либо оценить с
хорошей точностью (~1,5%) по классическим формулам [2] через спектральные
моменты. Действительно в классическом случае АКФ
- амплитуды линий. Необходимые при
расчетах спектров константы можно рассчитать непосредственно, либо оценить с
хорошей точностью (~1,5%) по классическим формулам [2] через спектральные
моменты. Действительно в классическом случае АКФ ![]() и
функции памяти
и
функции памяти ![]() имеют следующие разложения в
ряд Тейлора:
имеют следующие разложения в
ряд Тейлора:
В свою очередь
АКФ ![]() связана с соответствующими функциями
памяти
связана с соответствующими функциями
памяти ![]() интегро-дифференциальными уравнениями:
интегро-дифференциальными уравнениями:
Подставляя разложения и в и после несложных алгебраических преобразований можно получить:
Здесь предполагается, что АКФ нормирована в 0, т.е. С(0) = 1. Выражения и удобно представить в виде детерминантов матриц:
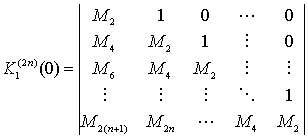 ,
(19)
,
(19)
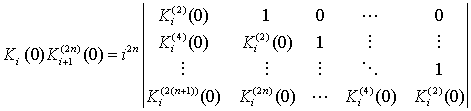 ,
(20)
,
(20)
где n=0,1,2,… . Справедливы и обратные соотношения, например:
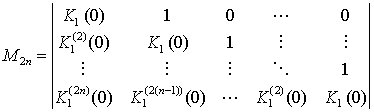 .
(21)
.
(21)
Таким образом, зная моменты ![]() , можно
рассчитать значения всех функций памяти и их производных
, можно
рассчитать значения всех функций памяти и их производных ![]() при t = 0. С другой стороны, зная
при t = 0. С другой стороны, зная ![]() можно вычислить все моменты
можно вычислить все моменты ![]() .
.
Предложенная модель позволяет улучшить описание микроволнового и субмиллиметрового спектров поглощения атмосферных паров воды.
На рис. 4 сопоставлены полуширины линий для используемых методик. Параметры линий приведены в Таблице 1. На рис. 5 дано сравнение спектров поглощения атмосферы при нормальных атмосферных условиях: сплошная линия – формула , штриховая линия – программа MPM2, пунктирная линия с кругами – формула . Видно, что разработанная нами методика лучше, чем программа MPM2 соответствует усредненным экспериментальным данным.

Рис.4 Сопоставление используемых полуширин линий в модели MPM2 и в данной работе.

Рис.5 Спектр поглощения атмосферы при нормальных атмосферных условиях: сплошная линия – формула , штриховая линия (------) – программа MPM2, пунктирная линия (……….) – [25], символы – усредненные экспериментальные данные.
Таблица 1
Вращательные переходы молекулы воды H2O16 в диапазоне частот 0<n<40см-1
|
k |
|
|
|
|
|
|
|
1 |
0,74 |
446,5 |
447,24 |
0,09019 |
0,626 |
0,1226 |
|
2 |
6,12 |
136,15 |
142,27 |
0,096 |
0,649 |
0,6230 |
|
*3 |
10,69 |
1283,02 |
1293,71 |
0,07652 |
0,42 |
2,584 |
|
4 |
10,88 |
315,73 |
326,61 |
0,09292 |
0,619 |
0,9741 |
|
5 |
12,67 |
212,16 |
224,83 |
0,0948 |
0,63 |
4,671 |
|
*6 |
14,53 |
1045,09 |
1059,62 |
0,05 |
0,29 |
1,232 |
|
7 |
14,63 |
742,09 |
756,72 |
0,0636 |
0,37 |
4,331 |
|
8 |
14,74 |
1045,09 |
1059,83 |
0,05023 |
0,332 |
3,753 |
|
9 |
15,0 |
285,4 |
300,4 |
0,08247 |
0,51 |
5,922 |
|
10 |
15,68 |
742,09 |
757,77 |
0,0629 |
0,38 |
1,617 |
|
11 |
15,8 |
488,2 |
504 |
0,069 |
0,38 |
1,839 |
|
12 |
16,3 |
602,7 |
586,4 |
0,0861 |
0,57 |
0,6458 |
|
*13 |
16,7 |
1394,9 |
1411,6 |
0,0424 |
0,32 |
4,962 |
|
14 |
18,58 |
23,79 |
42,37 |
0,1111 |
0,645 |
83,61 |
|
15 |
20,7 |
488,1 |
508,8 |
0,07606 |
0,6 |
7,408 |
|
*16 |
21,6 |
1789,1 |
1810,7 |
0,038 |
0,4 |
5,707 |
|
17 |
25,1 |
70,07 |
95,17 |
0,1044 |
0,69 |
52,08 |
|
*18 |
28,89 |
2225,57 |
2254,46 |
0,036 |
0,47 |
6,87 |
|
*19 |
30,21 |
1050,2 |
1080,41 |
0,0798 |
0,51 |
3,661 |
|
20 |
30,4 |
285,3 |
315,7 |
0,08638 |
0,676 |
4,901 |
|
21 |
32,3 |
383,9 |
416,2 |
0,08262 |
0,56 |
8,476 |
|
22 |
32,94 |
37,13 |
70,07 |
0,1032 |
0,66 |
24,87 |
|
23 |
36,6 |
136,76 |
173,36 |
0,09944 |
0,701 |
239,8 |
ПРИМЕЧАНИЕ: При k=13, 16 и 18 в каждом значении ![]() учтено
по две линии, частоты переходов которых совпадают, а именно: (77,0-86,3,
77,1-86,2), (88,1-97,2, 88,0-97,3)
и (99,0-108,3, 99,1-108,2)
соответственно.
учтено
по две линии, частоты переходов которых совпадают, а именно: (77,0-86,3,
77,1-86,2), (88,1-97,2, 88,0-97,3)
и (99,0-108,3, 99,1-108,2)
соответственно.
Метод оценки спектральных моментов
Рассчитать спектральные моменты можно как в рамках классической, так и квантово-механической теории. В случае квантово-механической теории оценочные выражения вплоть до четвертого спектрального момента были представлены Гордоном в [32]. Выражения для шестого спектрального момента полученные для классических ансамблей симметричных волчков и линейных молекул приведены в [33] и для асимметричных волчков в [34].
АКФ для классических ансамблей молекул типа жесткий ассиметричный волчок может быть записана как [34]
![]() (22)
(22)
где ![]() компоненты дипольного момента
молекулы,
компоненты дипольного момента
молекулы, ![]() - равновесные корреляционные функции, задаваемые как
- равновесные корреляционные функции, задаваемые как 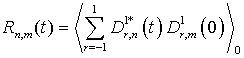 ,
, ![]() - D-функции Вигнера [35]. Таким образом, для оценки
производных АКФ достаточно найти производные равновесные корреляционные функции
- D-функции Вигнера [35]. Таким образом, для оценки
производных АКФ достаточно найти производные равновесные корреляционные функции
![]() :
:
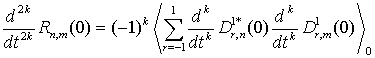 .
(23)
.
(23)
Принимая во внимание уравнения Эйлера [36], а именно,
![]() ,
(24)
,
(24)
 ,
(25)
,
(25)
![]() ,
(26)
,
(26)
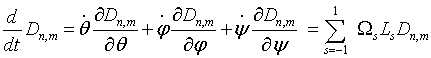 ,
(27)
,
(27)
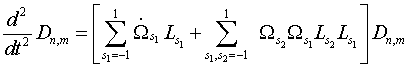 ,
(28)
,
(28)
где ![]() и операторы
и операторы ![]() определяются
как
определяются
как
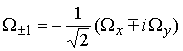 ,
, ![]() .
(29)
.
(29)
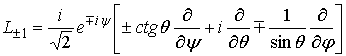 ,
,
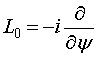 .
(30)
.
(30)
Действие операторов ![]() на D-функции Вигнера задается с помощью коэффициентов
Глебша-Гордана
на D-функции Вигнера задается с помощью коэффициентов
Глебша-Гордана ![]() [35]:
[35]:
![]()
Производные от угловых скоростей определяются уравнениями Эйлера [36]:
![]() ,
(32)
,
(32)
где Ix, Iy, Iz – главные моменты инерции молекулы,
![]() (34)
(34)
- момент сил, действующих на молекулу. После дифференцирования уравнений - также получим
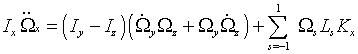 ,
(35)
,
(35)
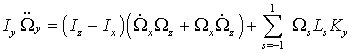 ,
(36)
,
(36)
 .
(37)
.
(37)
Компоненты K выражаются
через потенциальную энергию ![]() как
как
 ,
(38)
,
(38)
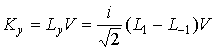 ,
(39)
,
(39)
![]() .
(40)
.
(40)
Всех выше приведенных соотношений
достаточно, чтобы найти производный функций ![]() при t = 0:
при t = 0:
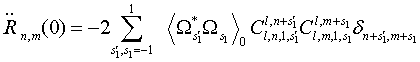 ,
(41)
,
(41)
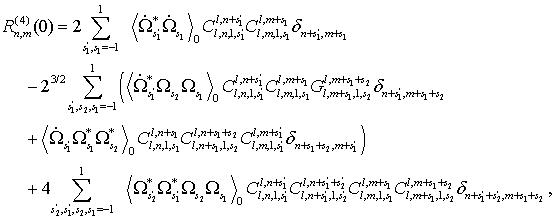 (42)
(42)
Здесь ![]() - символ Кронекера. Также учтено, что [35]
- символ Кронекера. Также учтено, что [35]
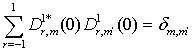 .
(43)
.
(43)
Дальнейшее упрощение связано с усреднением
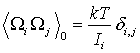 ,
, 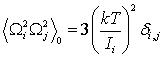 ,
, 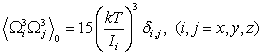 .
(44)
.
(44)
Окончательно получим
![]() ,
(45)
,
(45)
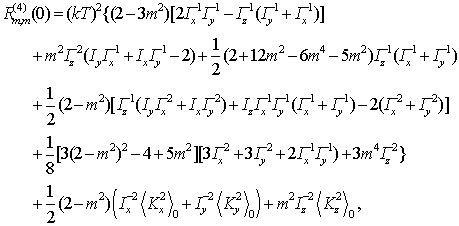 (46)
(46)
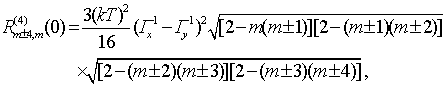 (47)
(47)
Соответственно спектральные моменты будут определяться как
![]() ,
(48)
,
(48)
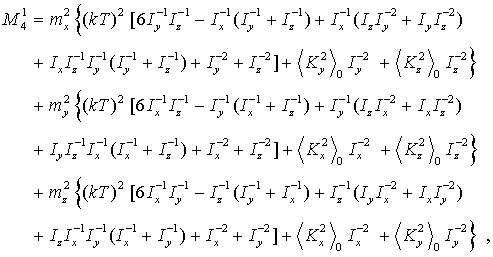 (49)
(49)
Наконец, искомые константы в выражении будут
(![]() ,
,![]() )
)
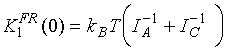 ,
(50)
,
(50)
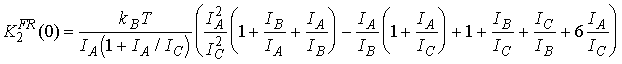 .
(51)
.
(51)
Заключение
Для описания ослабления в атмосферном водяном паре на длинах волн, больших 0,28 мм разработана простая инженерная методика расчета, основанная на эмпирической коррекции форм-фактора линии поглощения. Эта методика приводит в согласие теоретические данные с экспериментом в окнах прозрачности ММ и СбММ диапазонов в условиях земной атмосферы.
Разработан также единый теоретический подход к расчету широкополосных спектров дисперсии и поглощения полярных газов. Он основан на формализме функций памяти и применим для вычисления ослабления в атмосферных водяном паре и кислороде. Метод функций памяти может быть также применен для описания и анализа вращательных спектров поглощения полярных сред: полярных жидкостей в неполярном буфере, нематических жидких кристаллов.
Рассмотрена модель, объясняющая ряд аномалий молекулярного поглощения атмосферного водяного пара в микроволновом диапазоне. Результаты также могут быть применены при описании колебательно-вращательных спектров и спектров комбинационного рассеяния.
Авторы благодарны проф. Ю.П. Калмыкову, Е.П. Новичихину и К.А. Аганбекяну за полезные замечания.
1. Курс метеорологии, ред. П.Н. Тверской, Гидрометиздат, Ленинград, 1951.
2. Kalmykov Yu.P., Titov S.V. Advances in Chemical Physics, Wiley, New York, 1994, 87, p. 31.
3. Калмыков Ю.П., Титов С.В., Новскова Т.А. Радиотехника и электроника, 1998, 43, № 5, стр. 613.
4. Жевакин С.А., Наумов А.П. Изв. вузов. Радиофизика, 1963, 6, № 4, стр. 674.
5. Рядов В.Я., Шаронов ГА. Радиотехника и электроника, 1966, 11, № 6, стр. 1037.
6. Рядов В.Я., Фурашов Н.И. Изв. вузов. Радиофизика, 1966, 9, № 5, стр. 859.
7. Наумов А.П. Тр. Всесоюз. школы-симпоз. по распространению мм- и сбмм-волн в атмосфере, М.: ИРЭ АН СССР, 1983, стр. 21.
8. Frenkel L.// J.Mol.Spectroscopy. 1968. V.26. No.2. Р.227.
9. Гайкович К.П., Наумов А.П. Радиотехника и электроника, 1980, 25, № 8, стр. 1763.
10. Burch D.E., Gryvnak D.A. // Atmospheric water vapour. N.Y.: Academic Press. 1980. Р.47.
11. Соколов А.В.// Итоги науки и техники. Радиотехника. М.: ВИНИТИ. 1978. т.5. C. 5.
12. Аганбекян К. А., Зражевский А.Ю., Колосов М.А., Соколов А.В. // Радиотехника и электроника. 1971. т.16, №9, С. 1564.
13. Соколов А.В. Итоги науки и техники. Радиотехника, М.: ВИНИТИ, 1978, 5, стр.5.
14. Аганбекян К.А. Исследование распространения радиоволн субмиллиметрового диапазона в атмосферных парах воды, М.: ИРЭ РАН, 1970.
15. Аганбекян К.А.. Зражевский А.Ю., Соколов. А.В., Строганов Л.И. Исследование ширины и формы спектральной линии 0.92 мм в чистых парах воды. Радиотехника и электроника, 1975, 20, № 6, стр. 1155-1163.
16. Аганбекян К.А., Зражевский А.Ю., Малинкин В.Г. Радиотехника и электроника, 1974, 20, №11, стр. 2233.
17. Зражевский А.Ю., Аганбекян К.А. Всес. Симпоз. По приборам. Технике и распространению ММ и СбММ волн в атмосфере, М.: ИРЭ АН СССР, 1976, стр.230.
18. Зражевский А.Ю. Исследование влияния водяного пара на распространение радиоволн ММ и СбММ диапазонов, диссертация на соискание ученой степени кандидата технических наук, М.: ИРЭ АН СССР, 1976, 217 стр.
19. Аганбекян К. А., Зражевский А.Ю., Колосов М.А., Соколов А.В. Сб.IX Всес. Конф. По распростр. Радиоволн. Харьков ФТИ АН УССР, 1969, ч.2, стр. 126.
20. Аганбекян К.А., Зражевский А.Ю., Краевский В.И., Малинкин В.Г. Сб. Исследования в области радиотехники и электроники. М.: ИРЭ АН СССР, 1974, ч.1, стр. 141.
21. Clough S.A., Kneizys F.Х., Davies R.W. et al. Atmospheric water vapour, Acad. Press, N.Y., 1980, p. 25.
22. Clough S.A., Davies R.W., Tipping R.H. Spectral line shapes, 1983, 2, p.553.
23. Rosenkranz P.W. IEEE Trans. Anten. Proparg., 1975, AP-23, 4, p.498-506.
24. Liebe H. Radio Science, 1985, 20, 5, p. 1069-1089.
25. Зражевский А.Ю. Радиотехника и электроника, 1976, 21, №5, стр. 951-957.
26. Burroughs W.J., Jones R.G., Gebbie H.A. J. Quant. Spectr. Radiat. Trans., 1969, 9, 6, p. 809.
27. Benedict W. S., Kaplan L.D. J.Chem. Phis., 1959, 30, 2, p. 388.
28. Свердлов Б.А., Фурашов Н.И. Сб. 10 Всес. конф. по распр. Радиоволн, М.: Наука, 1972, стр. 52.
29. Калмыков Ю.П., Титов С.В. Зарубежная радиоэлектроника, 1998, № 9, стр. 32.
30. Kalmykov Yu.P., Titov S.V. J.Mol.Structure, 1999, 479, 2-3, p. 123.
31. Калмыков Ю.П., Титов С.В.// Электромагнитные волны и электронные системы, 1997, 2, № 4. стр. 80.
32. Gordon R. G. J. Chem. Phys., 1963, 39, p. 2788; 1963, 38, p. 1724; 1964, 41, p. 1819; 1964, 40, p. 1973.
33. St. Pierre A. G., Steele W. A. Mol. Phys., 1981, 43, p. 123.
34. Kalmykov Yu.P., Titov S.V. Mol.Phys., 2000, 98, 22, p. 1907.
35. Varshalovich D. A., Moskalev A. N., Khersonskii V. K. Quantum Theory of Angular Momentum. Word Scientific, Singapore, 1988.
36. Ландау Л.Д., Лифшиц Е.М.// Теоретическая физика. Том 1. Механика. Наука, Москва, 1988.
37. Ашымканов К.Ш.// Радиофизические характеристики атмосферы Северного Кыргыстана в КВЧ диапазоне. ИФПТМ НАН КР, Бишкек, 2011.
38. А.Ю. Зражевский, В.А. Паршуков, А.Н. Рукина. Е.П. Новичихин, «Влияние метеоусловий приземного слоя воздуха на рефракцию ММ и оптических волн». // Сборник «Тезисы, лекций и докладов 2 Всес. школы-симпозиума по распространению ММ и СБММ волн в атмосфере», Фрунзе, Илим, 1986, с 46-48.