Способ компьютерной диагностики болезни Паркинсона

УДК 618.8/831.2-072: 621.317.1

СПОСОБ КОМПЬЮТЕРНОЙ ДИАГНОСТИКИ БОЛЕЗНИ ПАРКИНСОНА

Ю. Н. Кликушин, В. Ю. Кобенко, А. А. Гошенков

Омский государственный технический университет (ОмГТУ)

Получена 11 октября 2012 г.

Аннотация. Описан способ диагностики болезни Паркинсона, основанный на измерении степени регулярности-хаотичности корреляционной функции сигнала ЭЭГ пациента. Разделение пациентов на группы больных и здоровых производится путем сортировки и фильтрации записей в базе данных результатов измерений. Предлагаемый способ позволяет также классифицировать пациентов по степени развития заболевания.

Ключевые слова: алгоритм, болезнь Паркинсона, диагностика, идентификационные параметры сигналов, степень регулярности-хаотичности, характеристическая частота.

Abstarct. A method for diagnosis of Parkinson's disease, based on the measurement of the degree of regularity-randomness of the correlation function of the patient's EEG signal is described. Separation of patients into groups of patients and healthy is by sorting and filtering records in a database of measurement results. The proposed method allows to classify patients according to the degree of development of the disease.

Keywords: algorithm, Parkinson's disease, diagnosis, identification signal parameters, the degree of regularity-randomness, the characteristic frequency.

Введение

Задача объективного оценивания состояния здоровья человека с использованием аппаратно-программных (компьютерных) средств является весьма актуальной. При построении компьютерных систем диагностики все чаще стали использоваться новые информационные технологии (нейронные сети [1], вейвлет-анализ [2,3], нечеткие модели [4,5], фракталы [6-8]) распознавания образов. По сравнению с классическим подходом, основанным на методах теории вероятности, эти технологии обеспечивают (при правильном методическом обеспечении процедур анализа сигналов) более высокое качество принятия решений.

Однако, на практике, чаще всего применяется такая технология анализа данных, которая компилирует вероятностные и информационные методы.

Характерным примером в этом отношении является работа [9], в которой описана технология автоматического распознавания корреляционных функций сигналов ЭЭГ, применительно к диагностике болезни Паркинсона. Подтверждая теоретическую обоснованность полученных в этой работе результатов и их ценность для практики построения автоматических диагностических систем, авторы данной статьи, тем не менее, предлагают собственный способ диагностики, основанный на идеях и методах теории идентификационных измерений, систематически изложенной в монографиях [10, 11] и кратко представленной, например, в ряде статьей [12-14].

Цель данной работы – описать идентификационный способ автоматического распознавания корреляционных функций сигналов ЭЭГ, применительно к диагностике болезни Паркинсона. Это необходимо для того, чтобы заинтересованные специалисты могли оценить возможные перспективы применения предлагаемого способа в решении и других задач медицинской диагностики.

Методика и инструменты исследования

Для лучшего понимания последующих рассуждений, примем постановку задачи исследования, принятой в работе [9]. При этом записи ЭЭГ рассматриваются как случайные шумы электрического потенциала работы головного мозга. В качестве информативных источников используются корреляционные функции сигналов ЭЭГ, параметры которых и служат оценками для формирования диагностических решений.

Наше предложение сводится к тому, чтобы, во-первых, рассматривать корреляционные функции как сигналы и, во-вторых, измерять в этих сигналах относительное содержание регулярной (или хаотической) компоненты. Показатель, количественно оценивающий свойство регулярности-хаотичности, в дальнейшем будем называть степенью регулярности («Regul») с диапазоном от 0 до 1. Если Regul = 0, сигнал полностью хаотический (случайный). Если Regul = 1, сигнал полностью регулярный (не случайный). Понятие «регулярный сигнал» в данном случае включает, как частный случай, строго периодические сигналы.

В основе предлагаемого способа диагностики лежит гипотеза о том, что предельные, качественные («абсолютно здоров» и «абсолютно болен») состояния объектов диагностики отображаются предельными значениями степени регулярности-хаотичности и, соответственно, должны находиться на противоположных концах шкалы 0≤Regul≤1. Другими словами, желательно проверить, имеет ли болезнь Паркинсона шкалу проявлений, коррелирующую со шкалой типа «Regul».

Идея предлагаемого способа состоит в том, чтобы равномерно и случайным образом (и без повторений) перемешать индексы всех отсчетов идентифицируемой корреляционной функции, превратив ее, тем самым, в подобие случайного сигнала. При таком алгоритме случайная реплика сохраняет значения всех отсчетов, форму и параметры распределения исходной корреляционной функции. Но особенно важно то, что при таком преобразовании изменяется важнейший идентификационный параметр сигнала – характеристическая частота.

В отличие от классической теории сигналов [15], идентификационная теория вводит понятие характеристической частоты, как частости появления экстремальных значений сигнала за время наблюдения. Это дает возможность оценивать частоту любых сигналов, в том числе случайных.

Физический смысл понятия «характеристическая частота» состоит в том, что для периодических сигналов ее значение совпадает с реальной, физической частотой. Для случайных сигналов характеристическая частота (F_c) связана с их формой распределения в соответствие с данными работы [13]. В табл. 1, для случайных сигналов с симметричными распределениями: двумодальным (2mod), арксинусным (asin), равномерным (even), трапецеидальным (trap), треугольным (simp), нормальным (gaus), двусторонним экспоненциальным (lapl) и Коши (kosh), даны оценки основных идентификационных показателей – параметра формы (А) и характеристической частоты (Fc). В соответствие с принятой в [11] терминологией, табл. 1 называется идентификационной шкалой (ИШ) распределений.

Таблица 1

Идентификационная шкала распределений симметричных случайных сигналов

(объем реализаций N = 10000, количество реализаций L = 100)

N=10000, L=100	Вид распределения случайного сигнала
N=10000, L=100	2mod	asin	even	trap	simp	gaus	lapl	kosh
Rank	1	2	3	4	5	6	7	8
A	4	6,28	8	10	12	19	36	3000
F_c	2500	2027	1667	1350	1180	736	416	6
Аналог	Squ-1	Sin-1, cos-1	Tri-1, saw-1

В строке «Аналог» указаны имена периодических сигналов единичной частоты (F = 1) прямоугольной (squ), синусоидальной (sin), косинусоидальной (cos), треугольной (tri) и пилообразной формы (saw), имеющих такие же значения параметра формы, как и у случайных сигналов с двумодальным (A₂_mod = A_squ), арксинусным (A_asin = A_sin = A_cos) и равномерным (A_even = A_tri = A_saw) распределениями.

В процессе проведения исследований была установлена новая для теории сигналов закономерность, в соответствие с которой:

. (1)

Соотношение (1) следует читать так: «Характеристическая частота Fc случайного сигнала всегда больше или равна характеристической частоте Fx любого другого сигнала с таким же значением параметра формы (или с тем же распределением мгновенных значений)».

На рис. 1 представлены инструменты, выполненные в среде LabVIEW и реализующие предлагаемый способ с помощью алгоритма равномерного, случайного перемешивания отсчетов входной выборки сигнала. Основной модуль преобразователя (RSA-tester) содержит два идентификационных тестера (FRaSH.vi), миксер (Mixer.vi), цикл (For-Next) и измерительную цепь, предназначенную для вычисления степени регулярности (Regul, %).

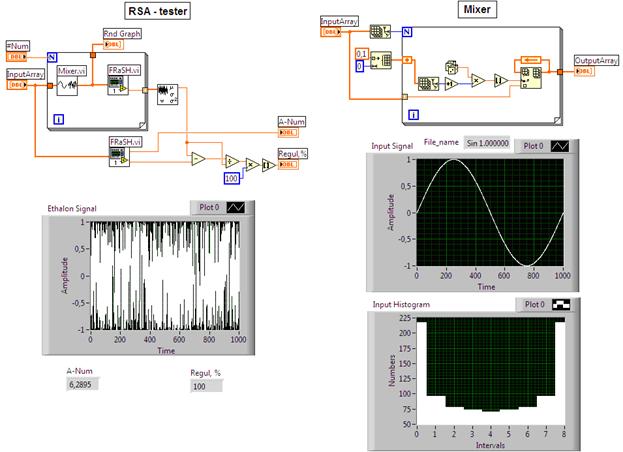
Рис. 1. Структура и компоненты преобразователя сигналов

Нижний по схеме идентификационный тестер измеряет параметр формы (А-Num) и характеристическую частоту (Fx) массива (Input Array) входного сигнала, в соответствие с табл. 1. Верхний по схеме идентификационный тестер измеряет характеристическую частоту (Fi) перемешанного массива, полученного из входного сигнала. Миксер непосредственно реализует функцию перемешивания номеров отсчетов входного сигнала. Количество перемешиваний задается с панели управления в окне #Num. Измеренные значения (Fi) усредняются. Степень регулярности (Regul, %) оценивается по формуле:

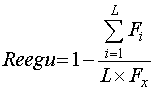(2)

где L – количество перемешиваний.

Принцип действия миксера заключается в следующем. Из исходного массива (Input Array) поочередно извлекаются значения отсчетов. Первоначальные индексы (i) этих отсчетов случайным образом (по равномерному закону) заменяются другими индексами (j), но так, чтобы не было повторений. В итоге на выходе миксера формируется новый массив тех же самых отсчетов, но с другими, случайными индексами (порядковыми номерами).

На дисплеях (рис. 1) отражены результаты тестирования преобразователя синусоидальным входным сигналом (File_name Sin-1,0) единичной частоты и объема выборки N = 1000. Выходной случайный сигнал (Ethalon Signal), называемый также репликой, имеет такой же объем, одинаковое с входным сигналом действующее значение (Uэфф = 0,707 В) и форму (A-Num = 6,2895 рад) распределения (Input Histogram).

При этом относительная разность характеристических частот (сигнала Fx = 1 Гц и реплики Fasin = 203 Гц для N = 1000) составила Regul = (203 -1)/203 = 0,995 или округленно ≈ 100%.

Тестирование преобразователя случайными сигналами, представленными своими реперными точками в ИШ (табл. 1), показало, что их регулярность в среднем близка к нулю, со стандартным отклонением в диапазоне от 1 до 10% (в зависимости от числа анализируемых реализаций).

В частности, в эксперименте с корреляционными функциями ЭЭГ, усреднение проводилось по 1000 реализациям, в результате чего случайная погрешность (с доверительной вероятностью 0,95) не превысила (1 – 1,8) % и что практически мало влияло на полное время анализа, составившее примерно 1 с.

Таким образом, с помощью предлагаемого способа действительно можно оценивать такие фундаментальные свойства сигналов, как регулярность-хаотичность.

Результаты исследований

Применим рассмотренную технологию к анализу нормированных корреляционных функций (данные взяты из работы [9]) группы больных и здоровых пациентов, табл. 2 и 3, соответственно, на предмет их регулярности-хаотичности.

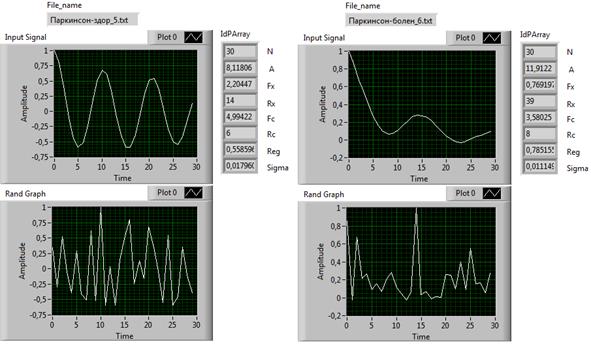
Рис. 2. Эпюры корреляционных функций и их случайные реплики для максимально удаленных объектов диагностики

На рис. 2 показаны эпюры корреляционных функций (Input Signal) и их случайные реплики (Rand Graph) для объектов №5_З и №6_Б диагностики, наиболее удаленных (в терминах расстояния) друг от друга.

В окнах типа «IdP Array» приведены оценки измеряемых при анализе величин (сверху-вниз): объем выборки (N), параметр формы (А), характеристическая частота (Fx) и разрешение (Rx) анализируемой корреляционной функции, характеристическая частота (Fc) и разрешение (Rc) случайной реплики, степень регулярности-хаотичности (Reg) в относительных единицах и случайная погрешность оценки степени регулярности-хаотичности.

Таблица 2

Корреляционные функции пациентов из группы больных

№ п/п	Номера корреляционных функций пациентов из группы больных
№ п/п	№1	№2	№3	№4	№5	№6
1	1	1	1	1	1	1
2	0,8338	0,7549	0,7883	0,8503	0,8319	0,8569
3	0,4876	0,3639	0,3448	0,551	0,5516	0,6731
4	0,1427	0,103	-0,0478	0,2517	0,348	0,5507
5	-0,1198	-0,0722	-0,2869	-0,0108	0,1989	0,4
6	-0,2357	-0,1539	-0,368	-0,2076	0,1071	0,2642
7	-0,1868	-0,1293	-0,3184	-0,2962	0,0736	0,1613
8	-0,0065	0,0105	-0,1926	-0,2654	0,0888	0,0932
9	0,227	0,2273	-0,0549	-0,1365	0,1348	0,0628
10	0,4194	0,4392	0,0374	0,0491	0,1912	0,0715
11	0,4938	0,5456	0,0557	0,2533	0,2367	0,1119
12	0,4195	0,4898	0,009	0,4177	0,2549	0,1582
13	0,229	0,3153	-0,0686	0,5025	0,2417	0,2132
14	-0,0025	0,1147	-0,1346	0,4948	0,205	0,2611
15	-0,1932	-0,0493	-0,1502	0,4047	0,1532	0,2796
16	-0,2822	-0,1466	-0,0935	0,2549	0,0971	0,2739
17	-0,2478	-0,1495	0,0361	0,0865	0,0539	0,2537
18	-0,1146	-0,0484	0,2123	-0,0618	0,0338	0,2115
19	0,061	0,114	0,371	-0,1627	0,0351	0,1551
20	0,2143	0,2646	0,4376	-0,1901	0,056	0,098
21	0,2923	0,3487	0,3916	-0,1353	0,0864	0,0464
22	0,2726	0,3328	0,2729	-0,0262	0,112	0,0042
23	0,1693	0,2224	0,1228	0,0946	0,1301	-0,0233
24	0,0254	0,079	-0,0342	0,2108	0,136	-0,0288
25	-0,1068	-0,0385	-0,1718	0,3061	0,1282	-0,0125
26	-0,1876	-0,103	-0,2614	0,3536	0,1121	0,0109
27	-0,201	-0,1024	-0,2831	0,3332	0,0912	0,0343
28	-0,1506	-0,036	-0,236	0,2606	0,0717	0,0535
29	-0,055	0,0744	-0,1459	0,1597	0,0556	0,0726
30	0,0508	0,1839	-0,0532	0,0477	0,0449	0,0915

Форма,рад.	10,5	10,7	11,8	10,7	14,2	11,9
Разрешение	19	18	23	21	38	39
Регулярность,%	60	58	65	65	73	78,5
Сигма(р=0,95),%	1,3	1,3	1,1	1,1	0,93	1,1

Таблица 3

Корреляционные функции пациентов из группы здоровых

№ п/п	Номера корреляционных функций пациентов из группы здоровых
№ п/п	№1	№2	№3	№4	№5
1	1	1	1	1	1
2	0,8694	0,7743	0,8432	0,7957	0,7983
3	0,5877	0,3358	0,4605	0,3917	0,3581
4	0,3011	-0,0402	0,0328	0,0591	-0,1012
5	0,0884	-0,2592	-0,2888	-0,0965	-0,4483
6	0,0068	-0,3027	-0,426	-0,0584	-0,5934
7	0,0692	-0,1881	-0,3528	0,1249	-0,5146
8	0,2466	0,0524	-0,0967	0,3541	-0,2374
9	0,4724	0,3192	0,2483	0,5174	0,1455
10	0,6538	0,4719	0,5447	0,5386	0,4944
11	0,7136	0,4246	0,6706	0,3757	0,6767
12	0,6284	0,1966	0,5758	0,1392	0,6161
13	0,4368	-0,0916	0,3048	-0,0629	0,3398
14	0,2167	-0,3125	-0,0286	-0,1499	-0,0417
15	0,0478	-0,391	-0,3013	-0,0928	-0,3891
16	-0,0195	-0,3065	-0,4287	0,0746	-0,5906
17	0,0277	-0,0992	-0,3812	0,2598	-0,5878
18	0,1631	0,1377	-0,1848	0,3585	-0,3859
19	0,3261	0,2894	0,0822	0,3224	-0,0525
20	0,4483	0,2865	0,3115	0,1744	0,2937
21	0,4831	0,1464	0,409	-0,003	0,5214
22	0,423	-0,062	0,3382	-0,1201	0,5434
23	0,2984	-0,2421	0,1359	-0,1347	0,3532
24	0,1606	-0,3112	-0,1103	-0,0599	0,0339
25	0,0571	-0,252	-0,3057	0,0585	-0,2893
26	0,0206	-0,0966	-0,3845	0,1602	-0,5022
27	0,0599	0,0866	-0,3266	0,1946	-0,5433
28	0,151	0,2151	-0,1601	0,1498	-0,4121
29	0,2527	0,2302	0,0465	0,0556	-0,158
30	0,3243	0,1281	0,2083	-0,0452	0,1304

Форма, рад.	9,8	10,9	8,9	11,3	8,1
Разрешение	17	17	15	17	14
Регулярность, %	58	55	56	55	56
Сигма(р=0,95), %	1,5	1,3	1,6	1,3	1,8

В нижней части таблиц размещены результаты измерений идентификационных параметров корреляционных функций пациентов.

К этим параметрам относятся: параметр формы (А, «Форма» с единицами измерения - радиан), разрешение и степень регулярности (Regul, «Регулярность», %). Показатель «Разрешение» определяет среднее количество отсчетов исходной выборочной реализации, размещенных на одном периоде характеристической частоты. Показатель «Сигма (р=0,95)» (измеряется в %) представляет собой оценку случайной погрешности (с доверительной вероятностью 0,95) определения степени регулярности, так, что результат измерения (%) может быть записан, как:

Результат = (Регулярность ±Сигма). (3)

Создадим реляционную БД идентификационных параметров (табл. 4) пациентов, в которой полями являются показатели «форма», «разрешение» и «регулярность». Для поиска скрытых (латентных) в БД закономерностей будем использовать самые простые операции реляционной алгебры – сортировку и фильтрацию записей.

Таблица 4

База данных идентификационных параметров пациентов

№ п/п	Обозначение объекта	Первичный диагноз	Параметр формы, А, рад.	Разре-шение	Регулярность, Regul, %	Примечание (окончатель-ный диагноз)
1	№1_Б	болен	10,5	19	60	болен
2	№2_Б	болен	10,7	18	58	пограничное состояние
3	№3_Б	болен	11,8	23	65	болен
4	№4_Б	болен	10,7	21	65	болен
5	№5_Б	болен	14,2	38	73	болен
6	№6_Б	болен	11,9	39	78,5	болен
7	№1_З	здоров	9,8	17	58	здоров
8	№2_З	здоров	10,9	17	55	здоров
9	№3_З	здоров	8,9	15	56	здоров
10	№4_З	здоров	11,3	17	55	здоров
11	№5_З	здоров	8,1	14	56	здоров

Сортировка БД по параметру формы дает перемешанный список больных и здоровых пациентов и, следовательно, закономерности нет. Сортировка по разрешению сразу же разделяет списки больных и здоровых по условию: «Если разрешение ≤17, то пациент – здоров. Иначе – болен».

Однако, поскольку разрешение, равное 17, имеют 3 корреляционные функции пациентов (№1_З, №2_З и №4_З), то, для повышения надежности разделения, необходимо использовать фильтрацию записей по двум полям и в такой последовательности: 1) степень регулярности и 2) разрешение.

Соответствующий алгоритм принятия решений, представленный в виде схемы на рис. 3, построен с использованием трех условий, что дает 4 варианта заключений, упорядоченных «по горизонтали».

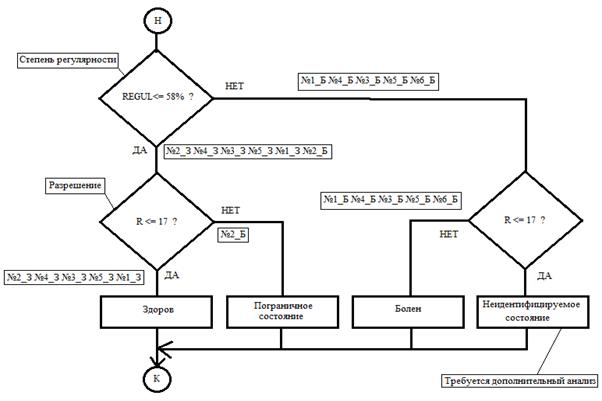
Рис. 3. Структура алгоритма принятия диагностических решений по результатам измерения идентификационных параметров корреляционных функций ЭЭГ

Это дает возможность разделить объекты не только на классы «больных» и «здоровых», но и на классы объектов с пограничным и неидентифицируемым состоянием. База данных может пополняться записями вновь обследованных пациентов, что должно способствовать повышению интеллектуальной мощности системы диагностики.

Выводы

Таким образом, результаты проведенных исследований, во-первых, подтверждают возможность использования предлагаемого способа для решения задачи диагностики болезни Паркинсона. Во-вторых, показано, что измерение идентификационных параметров корреляционных функций ЭЭГ, позволяет классифицировать состояния пациентов с упорядочиванием степени развития болезни. В-третьих, описанный алгоритм учитывает взаимосвязь идентификационных параметров (степени регулярности и разрешения), что повышает надежность принятия диагностических решений. Что касается статистической устойчивости предлагаемого способа диагностики, то этот вопрос требует дополнительных исследований с использованием более представительных выборок.

Работа выполнена при финансовой поддержке Минобрнауки РФ, в рамках государственного контракта № 16.516.11.6091 по теме «Проведение поисковых научно-исследовательских работ в области разработки и создания оборудования для диагностики и эксплуатации энергетического оборудования».

Литература

1. Куравский Л.С. Нейросетевая технология выявления аномалий электроэнцефалограмм // В кн. «Экспериментальная психология в России: Традиции и перспективы», под ред. В.А. Боровницкого - М.: Изд-во «Институт психологии РАН», 2010, с.111-117.

2. Ламброу Т., Линней А., Спеллер Р. Применение вейвлет-преобразования к обработке медицинских сигналов и изображений.// Компьютерра, №8, 1998, с.50.

3. Туровский Я.А., Мишин В.В., Битюцкая Л.А. и др. Вейвлетный анализ временных рядов вариабельности сердечного ритма//Известия вузов. Прикладная нелинейная динамика. – М.: 2002, Т. 10, №6, с. 16-23.

4. Карповский Е.Я., Бажора Ю.И., Карповская-Скорик Е.Е. Нечеткий классификатор для существенно малых выборок в задачах диагностики заболеваний// Материалы МНТК “Нечеткая логика, интеллектуальные системы и технологии” – Владимир, ВЛГУ, 1998, с. 16-18.

5. Горелова Н.А., Хрусталева Е.В. Пример использования «нечетких» методов в невролгии: дифференциальная диагностика миоклоний у детей // Интернет-публикация. Режим доступа: http://inftech.webservis.ru/it/conference/scm/2000/session 12/gorelova.htm

6. Анищенко В.С., Постнов Д.Э. Самоорганизация в хаосе. Новый метод экспериментальной диагностики. Письма в ЖТФ, 1990, т. 16, вып. 5, с. 28-32.

7. Меклер А.А. Применение аппарата нелинейного анализа динамических систем для обработки сигналов ЭЭГ // Вестник новых информационных технологий. – М.: 2007. Т. 14, № 1, с. 73-77.

8. Семенова Н.Ю., Захаров В.С. Анализ корреляционной размерности данных ЭЭГ при эпилепсии у детей // Нелинейный мир. – М.: 2010, № 3, с. 180-188.

9. Григорьев Ф.Н., Кузнецов Н.А. Задача распознавания образов для диагностики болезни Паркинсона по данным ЭЭГ // Интернет-публикация. – М.: ЖРЭ, Изд-во ИРЭ РАН, №1, 2012. Режим доступа: http://jre.cplire.ru/jre/jan12/8/text.html

10.Кликушин Ю.Н., Кошеков К.Т. Методы и средства идентификационных измерений сигналов: Монография. - Петропавловск: Изд-во СКГУ им. М.Козыбаева, 2007. -186 с.

11.Кликушин Ю.Н. Идентификационные инструменты анализа и синтеза формы сигналов: Монография. - Омск: Изд-во ОмГТУ, 2010. – 216 с.

12.Кликушин, Ю.Н. Количественная оценка свойств «регулярности-хаотичности» сигналов [Электронный ресурс] / Ю. Н. Кликушин // Журнал Радиоэлектроники - М.: Изд-во ИРЭ РАН. – 2006. – № 4. – Режим доступа: http://jre.cplire.ru.

13. Горшенков А.А., Кликушин Ю.Н. Представление моделей сигналов в системе идентификационных параметров// Интернет-статья. - М.: Журнал Радиоэлектроники, Изд-во ИРЭ РАН, № 9 (сентябрь), 2010 г. - http://jre.cplire.ru.

14. Горшенков А.А., Кликушин Ю.Н. Методы оценки хаоса сигналов// Измерение, информатизация, моделирование: проблемы и перспективы технологий, разработки и применения. - Ползуновский Вестник. - Барнаул, Изд-во АлтГТУ, №3(1), 2011, с.30-33.

15.Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Советское радио, 1977.