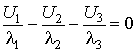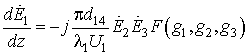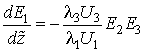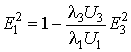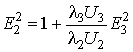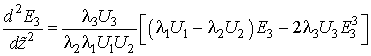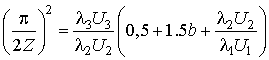УДК 537.8, 621.37
Преобразование когерентного ИК-излучения
в излучение терагерцового диапазона в планарном диэлектрическом волноводе [1]
В. В. Штыков
Национальный исследовательский университет «МЭИ»
Получена 13 апреля 2013 г., после доработки 21 апреля 2013 г.
Аннотация: Терагерцовая область частот до
последнего времени остается недостаточно изученной, что связано с отсутствием
как источников необходимой мощности, так и удобных приёмников. В работе рассмотрено
преобразование когерентного ИК-излучения ![]() -лазера в излучение с длиной волны около
100 мкм (3 ТГц) в нелинейном планарном диэлектрическом волноводе, выполненным
из монокристалла
-лазера в излучение с длиной волны около
100 мкм (3 ТГц) в нелинейном планарном диэлектрическом волноводе, выполненным
из монокристалла ![]() . Решено уравнение связанных волн. Найдены характеристики
такого преобразователя.
. Решено уравнение связанных волн. Найдены характеристики
такого преобразователя.
Ключевые слова: терагерцовый диапазон, нелинейность, преобразование частоты, диэлектрический волновод, уравнение связанных волн, фазовое согласование, эффективность преобразования.
Abstract: Terahertz band
(wavelengths from 1 mm up to 30 mm) remains little-studied up to the last-time,
this is connected with the lack of a powerful source of radiation, and
receivers. The work considers the conversion of coherent infrared radiation ![]() -laser to radiation with length of about 100 microns (3 THz) with
the nonlinear planar dielectric crystal
-laser to radiation with length of about 100 microns (3 THz) with
the nonlinear planar dielectric crystal ![]() waveguide. The
matching wave equation is solved. Characteristics of the conversion are found.
waveguide. The
matching wave equation is solved. Characteristics of the conversion are found.
Key words: Terahertz band, nonlinearity, frequency conversion, dielectric waveguide, matching wave equation, phase matching, energy-conversion efficiency.
Введение
Проблема генерации и регистрации терагерцового излучения, несмотря на определенные успехи в ее решении, остается актуальной. Наиболее значительные результаты в этом направлении достигнуты в квантовых каскадных лазерах, а также в источниках излучения, возбуждаемых оптическими импульсами фемтосекундной длительности. Однако такие источники все же достаточно сложны. Альтернативным источником излучения среднего и дальнего ИК диапазонов, работающим при комнатной температуре, может стать преобразователь частоты на основе нелинейного кристалла.
Генерация гармоник и комбинационных частот в нелинейных средах достаточно хорошо изучена (см. например, [1,2]). Генерация разностной частоты в средней части ИК диапазона (8–12 мкм) в двухчастотном полупроводниковом лазере исследовалась в [3]. В [4] сообщалось о преобразовании излучения CO2-лазера в излучение миллиметрового диапазона с частотой около 54 ГГц. Таким образом исследование возможности преобразования когерентного ИК-излучение в излучение терагерцового диапазона представляет интерес.
1. Постановка задачи
Геометрия задачи показана на рис. 1. Пластина, в которой распространяются взаимодействующие волны, представляет собой планарный диэлектрический волновод (ПлДВ). Он выполнен из материала, обладающий квадратичной нелинейностью, следствием которой является нелинейная поляризация [1, 2, 5].

Рис. 1. Геометрия задачи
![]()
Для кристалла класса ![]() (например,
(например, ![]() ) удобно
совместить ось
) удобно
совместить ось ![]() системы координат с направлением [111] кристаллической
структуры. В этом случае вектор нелинейной поляризации связан с полями простым
соотношением
системы координат с направлением [111] кристаллической
структуры. В этом случае вектор нелинейной поляризации связан с полями простым
соотношением
в котором тензор квадратичной
нелинейности заменен численным значением его элемента ![]() .
.
Свойства планарного диэлектрического волновода хорошо изучены (см, например, [6, 7]). Электрическая компонента поля основной моды ПлДв

 ;
; 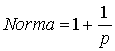 ,
,
где g, p – поперечные волновые числа.
В работе [3] экспериментально
исследовалось преобразование излучений с длинами волн ![]() мкм
и
мкм
и ![]() мкм. В этом случае длина волны разностной
частоты равна
мкм. В этом случае длина волны разностной
частоты равна  мкм[2].
Поскольку различия в значениях диэлектрической проницаемости малы, фазовое
согласование генерация на длинах волн
мкм[2].
Поскольку различия в значениях диэлектрической проницаемости малы, фазовое
согласование генерация на длинах волн ![]() и
и ![]() мкм возбуждалась на двух различных модах
ПлДВ.
мкм возбуждалась на двух различных модах
ПлДВ.
При решении задачи, в
отличие от [3], будем ориентироваться на преобразование двух частот ![]() -лазера c длинами волн 9,6 мкм и 10,6 мкм.
Первая из них соответствует генерации на квантовых переходах R-ветви, а вторая P-ветви колебательно-вращательного
спектра молекулы углекислого газа. В этом случае длина волны разностной частоты
равна
-лазера c длинами волн 9,6 мкм и 10,6 мкм.
Первая из них соответствует генерации на квантовых переходах R-ветви, а вторая P-ветви колебательно-вращательного
спектра молекулы углекислого газа. В этом случае длина волны разностной частоты
равна ![]() мкм.
мкм.
В общем виде уравнение для комплексных амплитуд связанных волн для трехволнового взаимодействия можно записать в следующем виде [2]
где ![]() .
.
Хорошо известно, что эффективное преобразование частоты происходит при выполнении условий фазового согласования [1–4]. Для ПлДВ это условие принимает следующий вид:
![]() .
.
Продольные волновые числа
удобно выразить через коэффициенты замедления  [7].
Тогда условие
[7].
Тогда условие ![]() примет вид
примет вид
Графическая иллюстрация
решения уравнения фазового согласования приведена на рис.2. Численное решение
уравнения (3) дает высоту ПлДВ ![]() (
(![]() мкм), которая обеспечивает фазовый
синхронизм взаимодействующих волн.
мкм), которая обеспечивает фазовый
синхронизм взаимодействующих волн.

Рис. 2. 1 и 2 – коэффициенты замедления исходных полей с длинами волн 9,6 мкм и 10,6 мкм , 3 – коэффициент замедления поля разностной частоты.
Высота ![]() (
(![]() мкм)
– полувысота ПлДВ, соответствующая фазовому согласованию взаимодействующих волн.
мкм)
– полувысота ПлДВ, соответствующая фазовому согласованию взаимодействующих волн.
Поскольку высота ПлДВ велика по сравнению с длиной волны исходных волн, условие фазового синхронизма можно записать следующим образом
![]()
или
 .
.
Если учесть, что по
указанным выше причинам ![]() , то можно получить
, то можно получить
 .
.
Это дает приближенное значение нормированной на ![]() высоты ПлДВ, которая обеспечивает режим
фазового согласования,
высоты ПлДВ, которая обеспечивает режим
фазового согласования,
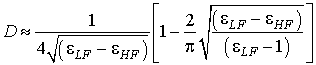 .
.
Приближенное значение
высоты ПлДВ для ![]() мкм и
мкм и ![]() мкм
равно 0,216 мкм, что находится в хорошем соответствии с численным решением
уравнения (3).
мкм
равно 0,216 мкм, что находится в хорошем соответствии с численным решением
уравнения (3).
В режиме фазового согласования система уравнений (2) принимает вид:
 (4)
(4)
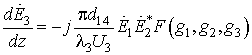
Здесь  – длина волны разностной частоты, которая
при
– длина волны разностной частоты, которая
при ![]() мкм и
мкм и ![]() мкм равна
101,76 мкм. Функция в (4) учитывает геометрию ПлДВ. Она равна
мкм равна
101,76 мкм. Функция в (4) учитывает геометрию ПлДВ. Она равна
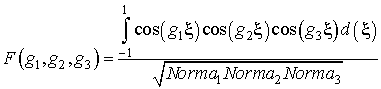 .
.
При 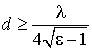 продольные волновые числа
продольные волновые числа ![]() ,
, ![]() , а
коэффициент замедления
, а
коэффициент замедления ![]() . В этом случае
. В этом случае
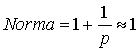 ,
,
а
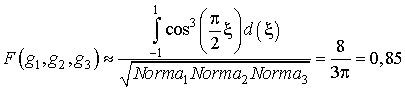
Систему уравнений (4) следует решить при граничных условиях
![]()
![]()
![]()
2. Решение системы уравнений
Если диссипации энергии
нет[3]
то, фазы полей ![]() и
и ![]() не
будут зависеть от продольной координаты, а волна разностной частоты будет
находиться по отношению к ним в квадратуре. Поэтому, представляя поля в форме
не
будут зависеть от продольной координаты, а волна разностной частоты будет
находиться по отношению к ним в квадратуре. Поэтому, представляя поля в форме
![]()
![]()
![]()
получаем
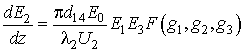 (5)
(5)

Если ввести эффективную продольную координату
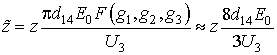 ,
,
то (5) преобразуется в систему связанных уравнений
 ;
(6)
;
(6)
![]() .
.
Особенность системы уравнений связанных мод в форме (6) состоит в том, что она не содержит в явном виде зависимостей от мощностей исходных волн.
Без потери общности для
системы (6) можно принять, что при ![]()
![]()
![]()
![]() . (7)
. (7)
Тогда решения ![]() по сути будут представлять собой коэффициенты
преобразования волн, зависящие от
по сути будут представлять собой коэффициенты
преобразования волн, зависящие от ![]() . Таким образом (6)
действительно позволяет решать задачу в наиболее общем виде.
. Таким образом (6)
действительно позволяет решать задачу в наиболее общем виде.
Численное решение системы уравнений (6) не представляет серьезной проблемы. Однако для выяснения потенциальных возможностей практического использования нелинейного преобразования желательно получить некоторые, пусть и приближенные, аналитические соотношения.
Прежде всего, сведем
систему уравнений (6) к одному нелинейному дифференциальному уравнению
относительно поля разностной частоты ![]() . Из первых двух
уравнений системы (6) при условиях (7) следует, что
. Из первых двух
уравнений системы (6) при условиях (7) следует, что
В результате получаем нелинейное дифференциальное уравнение второго порядка
Его следует решить при граничных условиях
![]() ,
, ![]() .
.
В отсутствии потерь зависимости амплитуд полей от продольной координаты будут представлять собой периодические функции. Поэтому решение можно представить в виде рядов Фурье с неизвестными коэффициентами
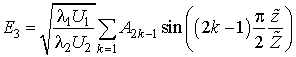
Эти ряды можно подставить в (6), провести интегрирование по пока еще неизвестному периоду и получить бесконечную систему алгебраических уравнений.
Найдем приближенное аналитическое решение, ограничившись только двумя членами ряда
Поле ![]() имеет максимум в точке
имеет максимум в точке ![]() , равный
, равный
![]() .
.
На коэффициенты ![]() и
и ![]() наложим
дополнительное условие
наложим
дополнительное условие ![]() т.е.
т.е. ![]() .
Тогда множитель A можно найти,
используя соотношения Мэнли-Роу [8], согласно которым максимальное значение
мощности волны разностной частоты равно
.
Тогда множитель A можно найти,
используя соотношения Мэнли-Роу [8], согласно которым максимальное значение
мощности волны разностной частоты равно

Для ПлДВ погонная мощность, проносимая через поперечное сечение единичной ширины, равна
 Вт/м.
Вт/м.
Это дает значение множителя
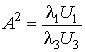 .
.
Подставляя (10) в (9) и
принимая во внимание условие ![]() , получаем систему из
двух алгебраических уравнений
, получаем систему из
двух алгебраических уравнений
Поделив второе уравнение на первое, получаем уравнение
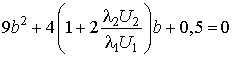 , (12)
, (12)
решение которого дает значение коэффициента
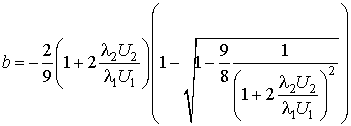
Точное решение уравнения
(12) для ![]() мкм и
мкм и![]() мкм дает
мкм дает
![]() и
и ![]() . Поскольку
в условиях фазового согласования
. Поскольку
в условиях фазового согласования ![]() ,
, ![]() и
и ![]() , то приближенная
оценка дает значение
, то приближенная
оценка дает значение
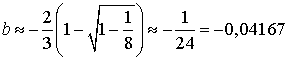 ,
,
которая не зависит от параметров конкретного ПлДВ и длин волн.
Из первого уравнения системы (11) находим значение
 .
.
Для длин волн ![]() мкм и
мкм и![]() мкм получаем
мкм получаем
![]() . Если пренебречь различием коэффициентов
замедления и принять
. Если пренебречь различием коэффициентов
замедления и принять ![]() , то
, то
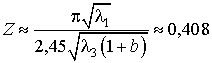 .
.
Если к тому же использовать ![]() , то
, то

Отклонение значительное, но для предварительных оценок вполне допустимое.
3. Результаты численного решения
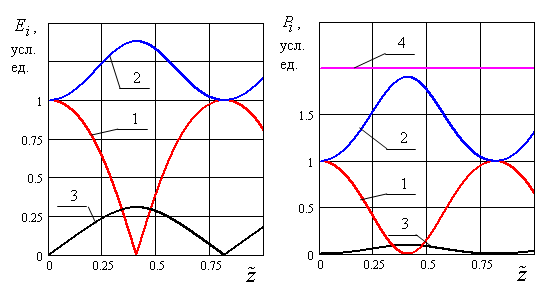
Результаты численного
решения уравнения (9), показаны на рис.3. Амплитуды волн ![]() и
и ![]() вычислены
с использованием соотношений (8). Периодичность решения хорошо просматривается.
Решение, удовлетворяет условию сохранения энергии, что иллюстрируется рис. 3.б.
Численное значение
вычислены
с использованием соотношений (8). Периодичность решения хорошо просматривается.
Решение, удовлетворяет условию сохранения энергии, что иллюстрируется рис. 3.б.
Численное значение ![]() .
.
а б
Рис.3. Результаты численного решения уравнения (9). Зависимости от эффективной продольной координаты амплитуд полей (а) и мощностей взаимодействующих волн (б). На рисунке: 1 и 2 – исходные волны, 3 – волна разностной частоты, 4 – суммарная мощность.
Зависимость напряженности
электрического поля разностной частоты в форме (10) для значений ![]() .
. ![]() и
и ![]() хорошо согласуется численным решением.
Отличие не превышает 0,3% (см. рис 4).
хорошо согласуется численным решением.
Отличие не превышает 0,3% (см. рис 4).
Если добавить в (10) слагаемое пятой пространственной гармоники, то ошибка уменьшается более чем в 3 раза. Однако в этом случае возможно только численное решение уравнений для определения весовых коэффициентов.
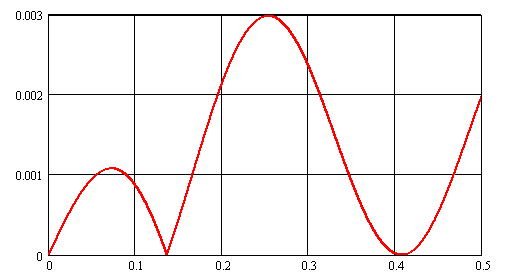
Рис. 4. Модуль разности численного решения исходного уравнения (9)
и приближенной пространственной зависимости (10)
для ![]() и
и![]()
![]() ,
, ![]() и
и ![]() .
.
4. Заключение
В заключение оценим энергетические параметры преобразования.
Численное значение нелинейная
константа монокристалла ![]() для генерации 2-ой
гармоники на длине волны 10,6 мкм
для генерации 2-ой
гармоники на длине волны 10,6 мкм ![]() приведено в [5].
Примем значение
приведено в [5].
Примем значение ![]() м/В для оценки эффективности преобразования
в разностную частоту. Диэлектрическая проницаемость
м/В для оценки эффективности преобразования
в разностную частоту. Диэлектрическая проницаемость ![]() на
низких частотах около
на
низких частотах около ![]() , а на высоких –
, а на высоких – ![]() [5].
[5].
Максимальная мощность
волны разностной частоты ![]() достигается, если
длина области взаимодействия
достигается, если
длина области взаимодействия ![]() , нормированная на
, нормированная на ![]() , удовлетворяет условию
, удовлетворяет условию

Если положить, что ширина
пучков исходных волн![]() , то мощности исходных волн
, то мощности исходных волн ![]() , необходимые для достижения максимума
, необходимые для достижения максимума ![]() , оказываются равными
, оказываются равными
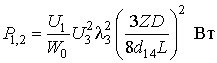 ,
,
а максимальная мощность разностной частоты –
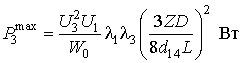
Подстановка числовых значений, найденных выше, при длине 3 см дает
![]() и
и ![]() .
.
Это вполне приемлемые уровни мощности не только для экспериментов по преобразованию частоты, но и для использования в качестве источником терагерцового излучения.
Все полученные выше результаты строго справедливы для среды без потерь. Учесть потери в (5) не представляет никаких трудностей. Однако в этом случае несправедливы соотношений Мэнли-Роу, а преобразование системы уравнений к одному становится невозможным. Это приведет к тому, что придется довольствоваться численным решением исходных уравнений и, как следствие, результаты такого решения будут носить, в определенном смысле, частный характер. Однако все же желательно иметь некоторые приближенные аналитические соотношения для принятия решения о возможности практического использования преобразования частоты в ПлДВ. Поэтому разумно оценить границы использования полученных результатов.
В качестве критерия можно
использовать условие малости затухания на длине ![]()

по сравнение с коэффициентом преобразования на той же длине в соответствии с соотношением Мэнли-Роу
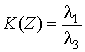 ,
,
т.е.

Условие на допустимое значение показателя затухания принимает вид
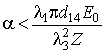 .
.
Соотношение содержит амплитуду исходной волны. Это связано с тем, что величина потерь растет пропорционально мощности, в то время как коэффициент преобразования пропорционален произведению мощностей исходных волн.
Для ![]() мкм и
мкм и![]() мкм,
мкм, ![]() м/В и
м/В и ![]()
![]() м-1.
м-1.
Если считать заданной длину области взаимодействия, то критерий становится совсем простым
 .
.
Для приведенной выше оценки эффективности преобразования на длине 3 см показатель затухания должен быть
![]() см–1.
см–1.
В окрестности длины волны
10 мкм затухание ![]() минимально. В справочнике [9]
приведены значения
минимально. В справочнике [9]
приведены значения ![]() для энергий
для энергий ![]() эВ. По-видимому, в интересующей нас
области длин волн
эВ. По-видимому, в интересующей нас
области длин волн ![]() . Хотя следует иметь в виду, что
для когерентного излучения важна тонкая структура поглощения.
. Хотя следует иметь в виду, что
для когерентного излучения важна тонкая структура поглощения.
Длину преобразователя в несколько сантиметров вряд ли можно считать удобной. Реально она видимо на порядок короче. Поэтому пренебрежение потерями тем более будет выполняться. Что касается поглощения на длине волны 100 мкм, то оно связано с взаимодействием электрических полей с носителями заряда. Его величину можно уменьшить, используя компенсированные полупроводники с высоким удельным сопротивлением.
Таким образом, приведенные выше выкладки могут оказаться полезными при исследовании и разработке методов генерации излучения терагерцового диапазона.
1. Ярив А. Введение в оптическую электронику. Пер. с англ./ Под ред. Богданкевича О.В. М.: Высшая школа, 1983. – 398 с.
2. Ярив А. Квантовая электроника и нелинейная оптика. Пер. с англ./ Под ред. Вендика О.Г. и Ханина Я. И. М.: Сов. радио, 1973. – 454 с.
3. Алёшкин
В.Я., Гавриленко В.И., Дубинов А.А. и др. Генерация разностной частоты в
двухчастотном полупроводниковом лазере ![]() // Сборник трудов международного оптического конгресса «Оптика
- XXI век». Т.1. «Фундаментальные проблемы оптики -– 2008», Т.2. «Всероссийский
семинар по терагерцовой оптике и спектроскопии». Санкт-Петербург. 20–24 октября
2008 / Под ред. Беспалова , Козлова С.А. – СПб.: 2008. – Т.1. 284 с., Т.2. 65 с.
// Сборник трудов международного оптического конгресса «Оптика
- XXI век». Т.1. «Фундаментальные проблемы оптики -– 2008», Т.2. «Всероссийский
семинар по терагерцовой оптике и спектроскопии». Санкт-Петербург. 20–24 октября
2008 / Под ред. Беспалова , Козлова С.А. – СПб.: 2008. – Т.1. 284 с., Т.2. 65 с.
4. Богаткин В. И., Лобов
Г.Д. Штыков В.В. Преобразование когерентного инфракрасного излучения в
миллиметровый диапазон в нелинейном кристалле ![]() // Квантовая электроника, 1973, 5,
129–134 с.
// Квантовая электроника, 1973, 5,
129–134 с.
5. Таблицы физических величин. Справочник. Под ред. акад. П.К. Кикоина. – М.: Атомиздат, 1976, – 1008 с.
6. Вайнштейн Л.А. Электромагнитные волны. – М.: Радио и связь, 1988. – 440 с.
7. Взягышев В.Ф. Диэлектрические волноводы. – М.. Сов. радио, 1970, –214 с.
8. Ахманов С.А., Хохлов Р.В. Проблемы нелинейной оптики – М.:ВИНИТИ, 1964, – 295 с.
9. Гавриленко В.И., Грехов А.М., Корбутяк Д.В, Литовченоко В.Г. Оптические свойства полупроводников. – Киев.:Наукова думка, 1987, – 608 с.