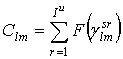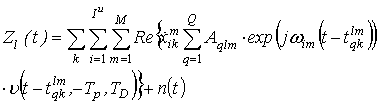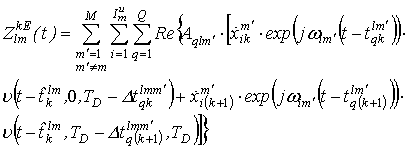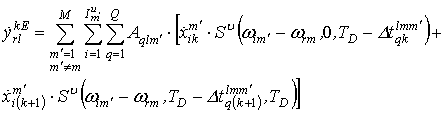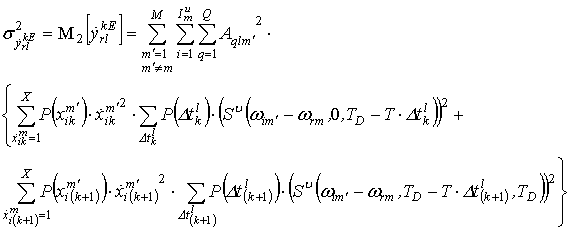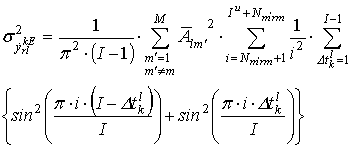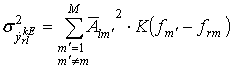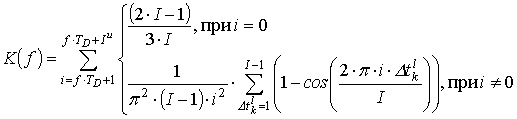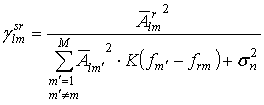УДК 621.396.49
ОЦЕНКА ГАРАНТИРОВАННОЙ ИНФОРМАЦИОННОЙ СКОРОСТИ ПЕРЕДАЧИ В СЕТЯХ ШИРОКОПОЛОСНОГО РАДИОДОСТУПА С УЧЕТОМ ВНУТРИСИСТЕМНЫХ ПОМЕХ
Е. А. Петрова
Казанский
национальный исследовательский технический университет
им А.Н. Туполева - КАИ
Статья получена 13 августа 2014 г., после доработки – 22 сентября 2014 г.
Аннотация. В работе рассматривается методика оценки информационной скорости передачи в фиксированных сетях широкополосного радиодоступа на основе разработанной оригинальной модели описания сигнально-помеховой обстановки. Приведено определение параметров модели и расчет информационной скорости передачи на фрагменте сети, развернутой в г. Казани.
Ключевые слова: сети широкополосного радиодоступа, информационная скорость, пропускная способность, битрейт, отношение сигнал/помеха.
Abstract: This paper presents the estimation method of the information rate on transfer in the fixed broadband radio access network’s based on the developed original signal-to-interference ratio description model. Model's parameters and the estimation of information rate on transfer are considered on a fragment of the network deployed in Kazan.
Key words: Networks of the broadband radio access, information rate, data throughput, bitrate, signal-to-interference ratio.
Введение
В последние годы развитие сетей широкополосного доступа получило новое ускорение. Основной причиной тому стали быстро развивающиеся рынки IP услуг. Сети широкополосного радиодоступа (ШПРД) позволяют без больших капитальных вложений оперативно обеспечивать абонентов всем спектром имеющихся в настоящее время интернет услуг.
Эти сети базируются на ряде перспективных технологий широкополосной передачи данных, основанных на применении ортогонально-частотной модуляции (OFDM).
Постоянно растущий спрос на услуги ШПРД приводит к резкому росту нагрузки на существующие сети, также увеличивается количество, как самих сетей, так и их операторов. В условиях ограниченности выделенного частотного диапазона все перечисленные факторы приводят к росту уровня взаимных помех, которые значительно снижают скорость передачи данных.
Этот вывод подтверждает анализ сети ШПРД стандарта 802.11n, развернутой в г. Казани на базе оборудования российского производителя ООО «Инфинет» [1].
Следовательно, оценка реальной информационной скорости в сетях ШПРД с учётом влияния внутрисистемных помех является актуальной задачей.
1. Методика оценки скорости передачи информации
Рассмотрим сеть связи, состоящую из ![]() базовых
станций (БС) и
базовых
станций (БС) и ![]() абонентских комплектов (АК). В
предположении о доминировании нисходящего трафика для этой сети нас будет
интересовать информационная скорость передачи данных от
абонентских комплектов (АК). В
предположении о доминировании нисходящего трафика для этой сети нас будет
интересовать информационная скорость передачи данных от ![]() -ой
БС до
-ой
БС до ![]() -го АК -
-го АК - ![]() .
.
Классический метод оценки указанной скорости предполагает, что приём сигнала осуществляется на фоне белого гауссова шума. Однако, как показано в [1], в реальности сигналы, передаваемые другими БС сети связи, также создают дополнительные внутрисистемные помехи.
На величину ![]() влияет большое количество
параметров:
влияет большое количество
параметров:
- битовая скорость передачи данных в канале, определяемая видом канальной модуляции и способом кодирования, образующими схему модуляции и кодирования (MCS) [2];
- процент ошибок пакетов;
- количество служебной информации, передаваемой в канале, включая заголовки пакетов, преамбулы кодов, циклические префиксы и т.д.;
- длина передаваемых информационных пакетов;
- параметры OFDM символов;
- количество OFDM символов в одном пакете и т.д.
Оценку гарантированного значения ![]() можно
провести несколькими способами, среди которых наибольшее распространение
получили следующие варианты:
можно
провести несколькими способами, среди которых наибольшее распространение
получили следующие варианты:
1) С использованием индекса модуляции и схемы кодирования (MCS) [2]. В этом случае необходимо учитывать, что данные по сети пересылаются в виде пакетов, передаваемых в каналах различных АК с различной битовой скоростью, зависящей от вида модуляции и кодирования (MCS), который в свою очередь определяется отношением сигнал/помеха на входе АК.
Отношение сигнал/помеха зависит от
номера поднесущей, поэтому вид MCS в
каждом из подканалов OFDM, для
ряда стандартов, может быть свой. Скорость передачи по нисходящему ![]() каналу на
каналу на ![]() поднесущих может быть вычислена как:
поднесущих может быть вычислена как:
где F – функция учета MCS; ![]() -
отношение сигнал/помеха (SNIR)
для
-
отношение сигнал/помеха (SNIR)
для ![]() -ой поднесущей.
-ой поднесущей.
2) На основе формулы Шеннона для пропускной способности в
единицу времени для канала с аддитивным белым гауссовым шумом (АБГШ) [3],
которая для ![]() -ой поднесущей будет иметь вид:
-ой поднесущей будет иметь вид:
где ![]() – количество OFDM символов в секунду.
– количество OFDM символов в секунду.
Для всего OFDM
сигнала пропускная способность в единицу времени будет определяться суммой
пропускных способностей ![]() :
:
Однако оба этих способа дают завышенные значения, так как не учитывают ряд вышеперечисленных факторов. Так на рисунке 1 приведен пример, полученный на участке сети, развернутой в г. Казани, показывающий, что увеличение битрейта может приводить к снижению реальной скорости передачи данных.
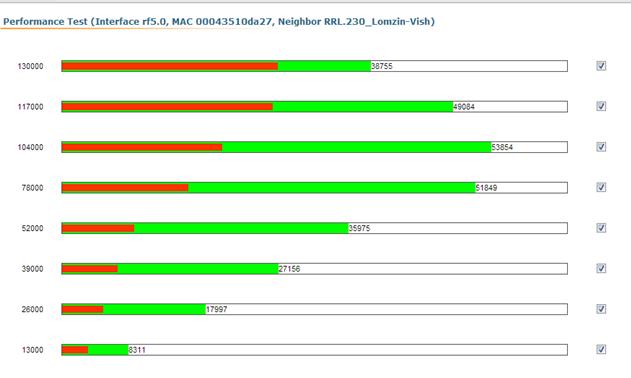
Рис.1. Реальная скорость передачи данных при различных значениях битрейта.
Красным выделено количество переповторов, при указанном слева значении битрейта в кбит/с. Справа указана реальная скорость передачи информации в кбит/с.
Так как полностью учесть влияющие на информационную скорость
факторы практически не возможно, предлагается перейти от задачи расчёта ![]() к оценке его значения на основе формулы
Шеннона:
к оценке его значения на основе формулы
Шеннона:
где ![]() - коэффициент учитывающий долю
информационной составляющей скорости передачи в пропускной способности канала
связи.
- коэффициент учитывающий долю
информационной составляющей скорости передачи в пропускной способности канала
связи.
Для расчета пропускной способности по формулам (1), (3), (4)
необходимо определить уровни сигнала и помех, входящих в ![]() .
.
2. Модель описания сигнально-помеховой обстановки
Существующие модели широкополосных OFDM сигналов рассматривают их как совокупность большого количества узкополосных ортогональных сигналов [4,5]. Однако в реальных условиях даже для фиксированных сетей связи, имеющих более чем одно передающее устройство, условия ортогональности сигналов часто нарушаются, что приводит к росту внутрисистемных помех. Поэтому необходимо разработать модель, обеспечивающую единообразное корректное описание сигнально-помеховой обстановки (СПО) в каналах с OFDM.
Рассмотрим модель сигнала одного OFDM символа. Он состоит из ![]() гармонических составляющих,
гармонических составляющих, ![]() из которых используются для передачи
данных, с учётом циклического префикса, на интервале времени
из которых используются для передачи
данных, с учётом циклического префикса, на интервале времени ![]() , где
, где ![]() -
длительность OFDM символа,
-
длительность OFDM символа, ![]() -
длительность циклического префикса, обычно равная
-
длительность циклического префикса, обычно равная ![]() .
Обозначив
.
Обозначив ![]() - модулированный
- модулированный ![]() -ый
кодовый символ, передаваемый на i-ой поднесущей, OFDM
сигнал может быть записан в виде:
-ый
кодовый символ, передаваемый на i-ой поднесущей, OFDM
сигнал может быть записан в виде:
где ![]() - время формирования
- время формирования ![]() -го кодового символа
-го кодового символа ![]() ;
; ![]() -
частота
-
частота ![]() -ой поднесущей;
-ой поднесущей; 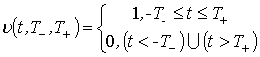 -
прямоугольный импульс.
-
прямоугольный импульс.
Основным фактором, влияющим на ошибки при приёме отдельного
OFDM сигнала, кроме шума измерения, является многолучёвое распространение
сигнала. Запишем сигнал на входе приёмного устройства для ![]() лучей в виде:
лучей в виде:
где ![]() - амплитуда
- амплитуда ![]() -го
луча
-го
луча ![]() сигнала
сигнала ![]() -го
передатчика на входе
-го
передатчика на входе ![]() -го приёмника;
-го приёмника; ![]() - модулированный
- модулированный ![]() -ый
кодовый символ
-ый
кодовый символ ![]() -го передатчика, соответствующий
i-ой поднесущей;
-го передатчика, соответствующий
i-ой поднесущей; ![]() - время прихода
- время прихода ![]() -го
луча
-го
луча ![]() -го кодового символа от
-го кодового символа от ![]() -го передатчика на вход
-го передатчика на вход ![]() -го приёмника;
-го приёмника; ![]() - реализация
белого гауссова шума.
- реализация
белого гауссова шума.
В связи с асинхронностью работы различных передающих
устройств при демодуляции OFDM
символа от ![]() -го передающего устройства на интервале
анализа
-го передающего устройства на интервале
анализа ![]() могут присутствовать сигналы двух
соседних кодовых символов:
могут присутствовать сигналы двух
соседних кодовых символов:
где ![]() - выбранное время приёма
- выбранное время приёма ![]() -го кодового символа
-го кодового символа ![]() -го передатчика.
-го передатчика.
Для сигнала, поступающего от ![]() -го
передатчика, будут выполняться условия ортогональности сигналов на различных
поднесущих. Для сигналов остальных передатчиков результат будет зависеть от
величины разности задержки передачи и выбранного времени приёма
-го
передатчика, будут выполняться условия ортогональности сигналов на различных
поднесущих. Для сигналов остальных передатчиков результат будет зависеть от
величины разности задержки передачи и выбранного времени приёма ![]() . Если указанная разность времён превышает
длительность циклического префикса
. Если указанная разность времён превышает
длительность циклического префикса ![]() , то произведение двух
прямоугольных импульсов приведет к появлению двух импульсов с длительностью не
равной
, то произведение двух
прямоугольных импульсов приведет к появлению двух импульсов с длительностью не
равной ![]() . Следовательно, такие сигналы будут
порождать внутрисистемные помехи.
. Следовательно, такие сигналы будут
порождать внутрисистемные помехи.
Для дальнейшего анализа разделим выражение (7) на две части.
В первую часть ![]() включим полезные сигналы приходящие от
включим полезные сигналы приходящие от ![]() -го передатчика и шум. Вторая часть
-го передатчика и шум. Вторая часть ![]() будет содержать сигналы остальных передатчиков, являющихся помехами. Для
этого случая можно записать:
будет содержать сигналы остальных передатчиков, являющихся помехами. Для
этого случая можно записать:
где  - комплексная амплитуда
- комплексная амплитуда ![]() -ой поднесущей от
-ой поднесущей от ![]() -го
передающего устройства на входе
-го
передающего устройства на входе ![]() -го приёмного.
-го приёмного.
В этом случае значения выходных символов на ![]() -ой
поднесущей
-ой
поднесущей ![]() будут определяться как сумма результатов
преобразований Фурье от
будут определяться как сумма результатов
преобразований Фурье от ![]() и
и ![]() . Первое слагаемое
. Первое слагаемое ![]() вычисляется
по формуле:
вычисляется
по формуле:
где ![]() -
комплексный отсчёт шума на выходе преобразования Фурье на частоте
-
комплексный отсчёт шума на выходе преобразования Фурье на частоте ![]() .
.
При рассмотрении второго слагаемого ![]() надо
учесть, что оно является суммой произведений двух сигналов: гармоники и
прямоугольного импульса. Соответственно значение его спектра на частоте
надо
учесть, что оно является суммой произведений двух сигналов: гармоники и
прямоугольного импульса. Соответственно значение его спектра на частоте ![]() будет определяться как сумма свёрток
спектров гармоники и прямоугольного импульса
будет определяться как сумма свёрток
спектров гармоники и прямоугольного импульса ![]() :
:
где ![]() - спектр прямоугольного импульса
- спектр прямоугольного импульса ![]() [6], а
[6], а ![]() -
количество поднесущих используемых
-
количество поднесущих используемых ![]() -ым передающим устройством.
-ым передающим устройством.
При работе системы значения модулированных символов ![]() и задержек
и задержек ![]() являются
случайными величинами. Следовательно, и помеха
являются
случайными величинами. Следовательно, и помеха ![]() также будет
являться случайной величиной.
также будет
являться случайной величиной.
Для цифровых систем связи величины ![]() и
и
![]() являются дискретными и характеризуются
своими распределениями вероятностей.
являются дискретными и характеризуются
своими распределениями вероятностей.
Так как стандартные алгоритмы приёма рассчитаны на гауссовское
распределение помех, то для оценки параметров распределения помех ![]() достаточно определить его математическое
ожидание и дисперсию.
достаточно определить его математическое
ожидание и дисперсию.
Математическое ожидание ![]() будет
определяться как:
будет
определяться как:
где ![]() - количество возможных символов.
- количество возможных символов.
В большинстве систем передачи распределение символов ![]() можно считать равномерным
можно считать равномерным ![]() . Кроме того, для всех первичных видов
модуляции, используемых в OFDM
системах
. Кроме того, для всех первичных видов
модуляции, используемых в OFDM
системах 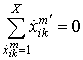 . Следовательно,
. Следовательно, ![]() .
.
Для указанного случая и с учётом независимости отдельных
слагаемых, входящих в (12), дисперсия ![]() может быть определена
как:
может быть определена
как:
Примем распределение вероятностей момента поступления сигнала
![]() равномерным. Тогда, при использовании для
вычисления значений
равномерным. Тогда, при использовании для
вычисления значений ![]() дискретного преобразования
Фурье, интервал дискретизации по времени определяется, как
дискретного преобразования
Фурье, интервал дискретизации по времени определяется, как ![]() , количество вариантов будет равно
, количество вариантов будет равно ![]() , а
, а ![]() .
.
При использовании на всех поднесущих сигналов с одинаковой
модуляцией и постоянство средней передаваемой мощностью сигнала можно считать 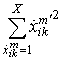 одинаковыми для всех устройств.
одинаковыми для всех устройств.
Кроме того, в реальных системах, как правило, разностная
частота сигнала и внутрисистемной помехи кратна минимальному частотному разносу
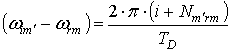 , где
, где ![]() - целое
число.
- целое
число.
В этом случае для одинакового количества используемых поднесущих у всех передающих устройств дисперсия помехи будет определяться как:
где ![]() - средняя мощность, поступающая от
передатчика с номером
- средняя мощность, поступающая от
передатчика с номером ![]() на вход приёмника
на вход приёмника ![]() по всем лучам.
по всем лучам.
Как видно из (15) дисперсия помех определяется мощностями
сигналов помех ![]() и некоторым коэффициентом,
учитывающим степень влияния помехи, зависящей от частотного разноса поднесущей,
на которой идёт передача и каналов помех.
и некоторым коэффициентом,
учитывающим степень влияния помехи, зависящей от частотного разноса поднесущей,
на которой идёт передача и каналов помех.
Обозначим ![]() - функцию, описывающую
вышеуказанный коэффициент. В этом случае можно записать:
- функцию, описывающую
вышеуказанный коэффициент. В этом случае можно записать:
где ![]() - средняя мощность сигнала от
- средняя мощность сигнала от ![]() -го передатчика на входе
-го передатчика на входе ![]() -го приемника,
-го приемника, ![]() -
частота передатчика помехи,
-
частота передатчика помехи, ![]() - частота поднесущей,
на которой осуществляется передача,
- частота поднесущей,
на которой осуществляется передача, ![]() - функция учитывающая
влияние помехи, рассчитываемая по следующей формуле:
- функция учитывающая
влияние помехи, рассчитываемая по следующей формуле:
где ![]() - общее количество поднесущих,
используемых в OFDM сигнале,
- общее количество поднесущих,
используемых в OFDM сигнале, ![]() - возможная задержка передачи OFDM символа, от момента его приёма.
- возможная задержка передачи OFDM символа, от момента его приёма.
На основе полученных выражений определено отношение сигнал/помеха на входе канального демодулятора:
Обозначим как
 -
-
коэффициент,
учитывающий вызванное многолучевым распространением отличие мощности полезного
сигнала на ![]() -ой поднесущей, от средней мощности. Тогда
искомое отношение сигнал/помеха можно записать как:
-ой поднесущей, от средней мощности. Тогда
искомое отношение сигнал/помеха можно записать как:
Влияние коэффициента ![]() учитывается
в теории битлоадинга [7]. Так как в применяемых в настоящее время стандартах,
такая функция не реализуется, влияние этого коэффициента учитывается в методе SNR Gap анализа, заключающегося во введении
некоторого коэффициента запаса
учитывается
в теории битлоадинга [7]. Так как в применяемых в настоящее время стандартах,
такая функция не реализуется, влияние этого коэффициента учитывается в методе SNR Gap анализа, заключающегося во введении
некоторого коэффициента запаса ![]() по отношению к уровню
сигнал/помеха [7].
по отношению к уровню
сигнал/помеха [7].
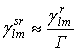 , (20)
, (20)
Учитывая, что как правило ![]() , можем записать:
, можем записать:
Неизвестные параметры ![]() и
и ![]() для сети определённого
стандарта, развёрнутой в определённых условиях, можно считать постоянными и
оценить при помощи критерия минимума среднеквадратичного отклонения на основе результатов
проведённых тестов:
для сети определённого
стандарта, развёрнутой в определённых условиях, можно считать постоянными и
оценить при помощи критерия минимума среднеквадратичного отклонения на основе результатов
проведённых тестов:
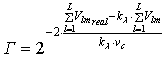 (23)
(23)
3. Определение параметров модели
Для фрагмента сети ШПРД стандарта 802.11n, развёрнутой в г. Казани, на базе оборудования российского
производителя ООО «Инфинет», при помощи выражений (22-23), на основании данных, приведенных в
таблице 1, были определены
параметры ![]() и
и ![]() равные 0,67 и 13,12
соответственно.
равные 0,67 и 13,12
соответственно.
Сравнение рассчитанных по формулам (1), (3), (21) и измеренной скоростей передачи информации приведено в таблице 1 и на рисунке 2.
Таблица 1. Рассчитанные и измеренные значения скоростей передачи информации.
|
АК |
|
|
|
Vreal , МБ/с |
|
АК_22_42 |
104 |
106 |
39.42 |
30.67 |
|
АК_22_46 |
117 |
111 |
42.45 |
34.87 |
|
АК_22_44 |
130 |
129 |
54.17 |
57.56 |
|
АК_22_57 |
130 |
143 |
63.91 |
67.38 |
|
АК_22_51 |
117 |
116 |
45.74 |
45.93 |
|
АК_62_OF |
117 |
118 |
47.15 |
34.19 |
|
AK_81_PU |
117 |
117 |
46.12 |
54.06 |
|
AK_22_92 |
104 |
104 |
37.91 |
47.66 |
|
AK_84_TAT |
130 |
129 |
54.18 |
50.07 |
|
BS_22_99 |
78 |
85 |
26.11 |
27.04 |

Рис.2. Сравнение рассчитанных и измеренных значений скоростей
передачи информации.
Анализ среднеквадратического отклонения экспериментальных и
расчетных данных показал, что ![]() МБ/с для
МБ/с для ![]() , рассчитанного по (21) с учетом
, рассчитанного по (21) с учетом ![]() и
и ![]() , для
, для ![]() (1) -
(1) - ![]() МБ/с, а для
МБ/с, а для ![]() рассчитанного по формуле (3)
рассчитанного по формуле (3) ![]() МБ/с.
МБ/с.
Для сравнения на том же фрагменте
сети был проведен расчет скорости передачи информации на основе формулы Шеннона
без учета влияния внутрисистемных помех (18) ![]() . Для
этого случая были определены параметры
. Для
этого случая были определены параметры ![]() и
и ![]() равные
0.27 и 1.2 соответственно. Результаты расчета представлены в
таблице 2 на рис. 3.
равные
0.27 и 1.2 соответственно. Результаты расчета представлены в
таблице 2 на рис. 3.
Таблица 2. Отношение сигнал/шум (SNR), рассчитанные и измеренные значения скоростей передачи информации.
|
АК |
SNR, дБ |
|
|
Vreal , МБ/с |
|
АК_22_42 |
35 |
151.15 |
39.89 |
30.67 |
|
АК_22_46 |
37 |
159.79 |
42.22 |
34.87 |
|
АК_22_44 |
44 |
190.02 |
50.38 |
57.56 |
|
АК_22_57 |
41 |
177.06 |
46.88 |
67.38 |
|
АК_22_51 |
41 |
177.06 |
46.88 |
45.93 |
|
АК_62_OF |
37 |
159.79 |
42.22 |
34.19 |
|
AK_81_PU |
43 |
185.70 |
49.21 |
54.06 |
|
AK_22_92 |
54 |
233.20 |
62.04 |
47.66 |
|
AK_84_TAT |
42 |
181.38 |
48.05 |
50.07 |
|
BS_22_99 |
26 |
112.33 |
29.41 |
27.04 |
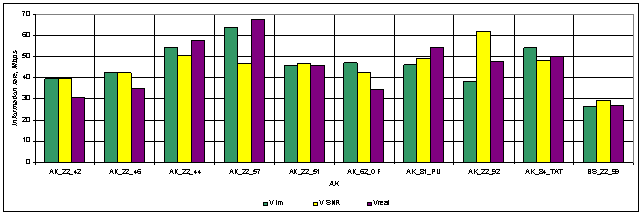
Рис.3. Сравнение
рассчитанной без учета внутрисистемных помех скорости передачи информации с
измеренной и рассчитанной по формуле (21).
Анализ среднеквадратического отклонения экспериментальных и
расчетных данных показал, что ![]() МБ/с для
МБ/с для ![]() , рассчитанного по формуле Шеннона без
учета внутрисистемных помех, но с учетом
, рассчитанного по формуле Шеннона без
учета внутрисистемных помех, но с учетом ![]() и
и ![]() .
.
Заключение
На основании приведенных результатов можно сделать следующие выводы:
1. Для получения корректных оценок скорости передачи информации необходимо учитывать долю передаваемой служебной информации.
2. Наименьшее
среднеквадратическое отклонение (7.4 МБ/с) дает метод оценки информационной
скорости на базе канальной скорости передачи, рассчитываемой по формуле Шеннона
на основе отношения сигнал/помеха, и коэффициентов ![]() , учитывающего
долю информационной составляющей, и
, учитывающего
долю информационной составляющей, и ![]() - запаса по отношению к уровню
сигнал/помеха.
- запаса по отношению к уровню
сигнал/помеха.
3. Классический
метод расчета с использованием отношения сигнал /шум, вместо отношения
сигнал/помеха, дает большее среднеквадратическое отклонение при явно заниженной
оценке доли информационной составляющей ![]() =0.27.
=0.27.
Следовательно, предложенная методика оценки гарантированной
информационной скорости на базе канальной скорости передачи, рассчитываемой по
формуле Шеннона на основе отношения сигнал/помеха, и коэффициентов ![]() , учитывающего долю информационной
составляющей, и
, учитывающего долю информационной
составляющей, и ![]() - запаса по отношению к уровню
сигнал/помеха дает
максимально приближенную к реальной ситуации картину в сетях широкополосного
радиодоступа.
- запаса по отношению к уровню
сигнал/помеха дает
максимально приближенную к реальной ситуации картину в сетях широкополосного
радиодоступа.
Литература
1. Выборнов О.В., Измайлов А.М., Козлов С.В., Спирина Е.А. Тестирование ЭМС оборудования стандарта 802.11n фирмы InfiNet. Вестник КГТУ им. А.Н. Туполева.№4, вып.2(68), 2012г.
2. Прогнозирование потенциальной нагрузки секторов сетей широкополосного радиодоступа на основе анализа отношения сигнал/помеха с использованием геоинформационных технологий / О.В. Выборнов, А.М. Измайлов, С.В. Козлов, В.Н. Лаврушев, Е.А. Спирина. - Вестник Казанского государственного технического университета им. А.Н. Туполева. 2013. №4.
3. Теория электрической связи: Учебник для вузов/ А.Г. Зюко, Д.Д. Кловский, В.И. Коржик, М.В. Назаров; Под ред. Д.Д. Кловского. – М., Радио и связь, 1999. – 432с.;204 ил.
4. Широкополосные беспроводные сети передачи информации, В.М. Вишневский, А.И. Ляхов, С.Л., Портной, И.В. Шахнович, Техносфера, М.2005г. 595с.
5. Schulze Henrik. Theory end Application of OFDM and CDMA. Wideband Wireless Communications / Henrik Schulze, Christian Luders // British library Cataloguing in Publication Data.: John Wiley & Sons, Ltd, 2005.
6. Баскаков С. И. Радиотехнические цепи и сигналы. М.: Высшая школа, 2000. – 462 с.
7. Моделирование процессов и явлений в системах связи: методическое пособие для самостоятельной работы магистров направления 210700.68 «Инфокоммуникационные технологии и системы связи» / Ворошилин Е.П.. – ТУСУР. Томск, 2012.