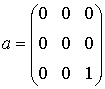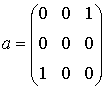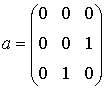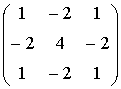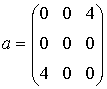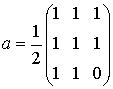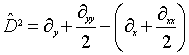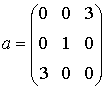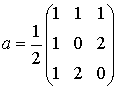| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2001 |  |
ИССЛЕДОВАНИЕ НЕАДАПТИВНЫХ ОПЕРАТОРОВ ДИСКРЕТНОЙ СВЕРТКИ ДЛЯ ОБРАБОТКИ ИЗОБРАЖЕНИЙ
Отдел медицинской физики, информатики и дозиметрии Владимирского областного онкологического диспансера
Получена 24 мая 2001 г.
Работа посвящена исследованию
неадаптивных операторов дискретной свертки (масок) размерности
![]() , применяемых
для обработки изображений. Получены выражения для эквивалентных
дифференциальных операторов, предложен метод классификации масок, метод
построения канонической формы маски для заданной исходной. Предложен метод
нахождения АЧХ ассоциированных частотных фильтров. Сформулирован ряд теорем.
, применяемых
для обработки изображений. Получены выражения для эквивалентных
дифференциальных операторов, предложен метод классификации масок, метод
построения канонической формы маски для заданной исходной. Предложен метод
нахождения АЧХ ассоциированных частотных фильтров. Сформулирован ряд теорем.
1. Введение
Как известно
[1], скользящие окна (маски), применяемые для
обработки изображений, представляют собой таблицы действительных чисел (весовых
коэффициентов) размером
![]() . Их действие на локальную область
изображения с центром в элементе fi,j состоит в усреднении с весами –
коэффициентами маски значений яркости элементов изображения в окне
. Их действие на локальную область
изображения с центром в элементе fi,j состоит в усреднении с весами –
коэффициентами маски значений яркости элементов изображения в окне
![]() .
.
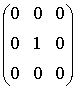
Так, значение
яркости элемента gi,j изображения - результата (назовем
его откликом) для маски
![]()

определяется из соотношения
Индексы i,j в (1) пробегают почти все значения, соответствующие размеру исходного изображения, за исключением граничных полос (в данном случае – за исключением первой и последней строки, а также первого и последнего столбца матрицы исходного изображения). Таким образом, результат требует доопределения границ [2], но учитывая, что размеры изображений обычно много больше размеров масок, неопределенными граничными элементами результата можно просто пренебречь и ограничиться изображением – результатом меньшего размера. Далее в этой статье рассматриваются неадаптивные маски, т.е. такие, коэффициенты которых постоянны (не зависят от координат или яркостей пикселов текущей области)
Наиболее
распространены в практике маски размера
![]() (Лапласа, Превитта, Собела, Кирша, Робертса
и т.д.) ввиду их высокой вычислительной эффективности. Выражение (1)
представляет собой определение дискретной свертки функции f с ядром M. Если представить непрерывную функцию f(x,
y), являющуюся образующей для дискретного
аналога fi,j , в виде разложения в ряд в
окрестности точки (x,.y)
(Лапласа, Превитта, Собела, Кирша, Робертса
и т.д.) ввиду их высокой вычислительной эффективности. Выражение (1)
представляет собой определение дискретной свертки функции f с ядром M. Если представить непрерывную функцию f(x,
y), являющуюся образующей для дискретного
аналога fi,j , в виде разложения в ряд в
окрестности точки (x,.y)
то можно реализовать свертку (1),
принимая p = h, q
= k.
Понятно, что в случае маски
![]() можно ограничиться в (2) частными
производными не выше второго порядка. Тогда
можно ограничиться в (2) частными
производными не выше второго порядка. Тогда
Здесь мы приняли обозначения
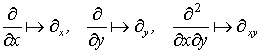 и т.д.
и т.д.
В пределе,
когда можно считать, что
![]() , (
, (![]() –
размер изображения), выражение (3)
определяет некоторый линейный дифференциальный оператор второго порядка
–
размер изображения), выражение (3)
определяет некоторый линейный дифференциальный оператор второго порядка
![]() , действующий
на непрерывную функцию изображения:
, действующий
на непрерывную функцию изображения:
Выражение (4)
можно трактовать как двумерную свертку функции f(x,
y) с ядром
![]()
Ядро свертки
![]() в этом случае является
обобщенной функцией на бесконечно малом носителе
в этом случае является
обобщенной функцией на бесконечно малом носителе
![]() (аналог
окна маски в дискретной области).
(аналог
окна маски в дискретной области).
Окончательно, выражение для дифференциального оператора, соотвествующего маске М будет следующим:
Предложенный подход открывает возможности классификации известных и создания новых ядер свертки для обработки изображений. В самом деле, линейный дифференциальный оператор второго порядка в общем виде может быть записан как
где матрица [amn] симметрична.
Если формально записать уравнение характеристик в виде
то ясно, что при заданной матрице amn оно описывает некоторое коническое сечение. Заметим, что вводимые нами термины и определения здесь и далее обозначаются курсивом. Маски, для которых a22 = 0 назовем однородными, в противном случае - неоднородными.
2. Классификация масок
Предлагается
классифицировать маски по типу конического сечения, соотвествующего уравнению
характеристик. Классификация конических сечений хорошо известна [3] (Приложение 1).
Например, применим этот принцип классификации к маске "Лаплас-1" ![]() . Согласно (6)
ей соответствует дифференциальный оператор
. Согласно (6)
ей соответствует дифференциальный оператор
![]() с характеристикой
с характеристикой
![]() , которая
описывает действительную точку пересечения двух мнимых прямых.
, которая
описывает действительную точку пересечения двух мнимых прямых.
Удобно далее записывать маски в матричных обозначениях (круглые скобки), имея в виду, однако, что для масок отсутствует понятие "матричного произведения", но сумма масок имеет смысл вследствие линейности (1). Таким образом, будем записывать маски в виде:
Тем не менее, если маске М поставить в соответствие матрицу mp,q, а дифференциальному оператору в (3) матрицу
то оказывается справедливой
Теорема 1
Сумма собственных значений
произведения ![]() равна
равна
![]()
3. Обратная задача
Обратная
задача, состоящая в нахождении коэффициентов маски Mс,
соответствующей заданному дифференциальному оператору
![]() , решается весьма
просто, если применить каноническое разложение. Легко убедиться, что
, решается весьма
просто, если применить каноническое разложение. Легко убедиться, что
 ,
,
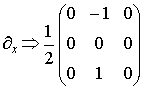 ,
,
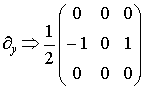 ,
,
Отсюда непосредственно следует, что
![]()
ß
Таким образом, применение канонического разложения (11) позволяет решить обратную задачу весьма простыми средствами, без привлечения дополнительных условий. Назовем маску вида (12) канонической. Опуская ряд громоздких преобразований, приведем выражение, прямо связывающее коэффициенты исходной и канонической масок:
Произвольной маске М и ее каноническому аналогу Мс соответствует один и тот же дифференциальный оператор, но их дискретные свертки с некоторым изображением f, вообще говоря, не совпадают. Это связано с тем, что мы ограничились в (3) производными второго прядка. Поэтому следует ожидать более точного совпадения откликов, если изображение не содержит слишком резких перепадов яркости.
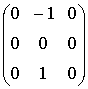
Приведем пример. Однородной маске Кирша
соответствует гипербрлический оператор (Приложение 2):
с матрицей характеристики (8)
Выражение для канонической маски Кирша согласно (13) будет следующим:
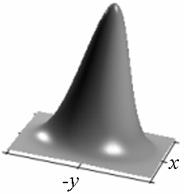
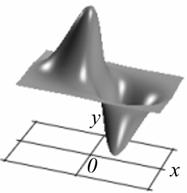
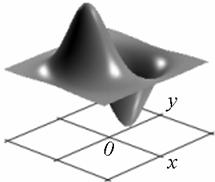
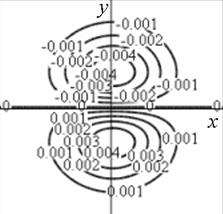
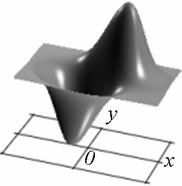
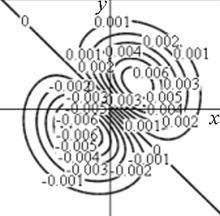
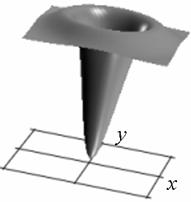
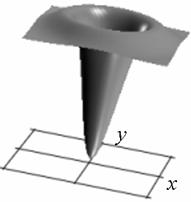
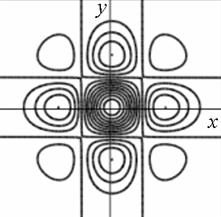
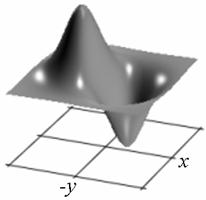
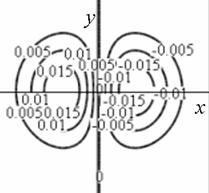
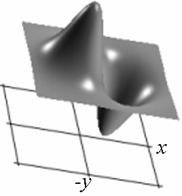
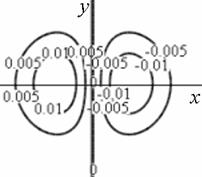
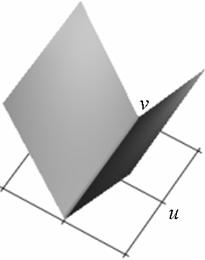
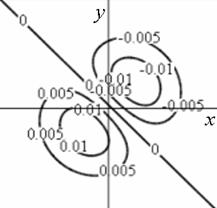
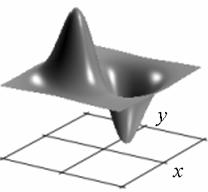
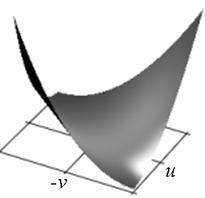
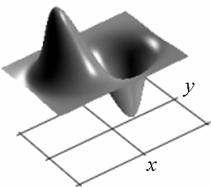
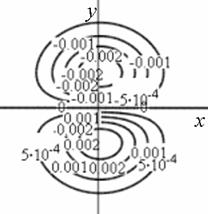
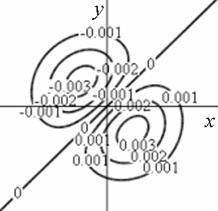
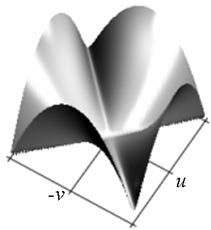
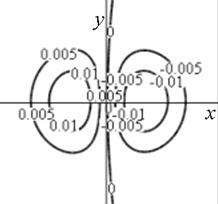
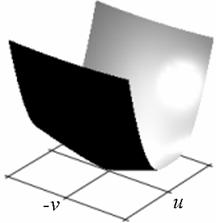
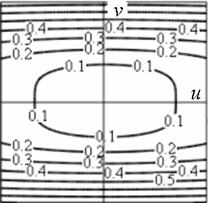
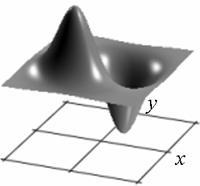
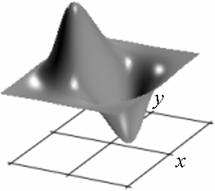
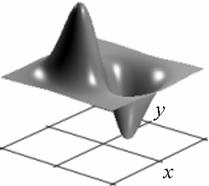
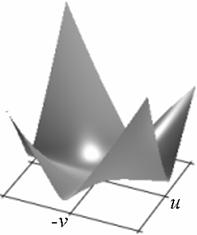
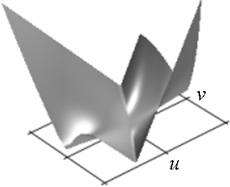
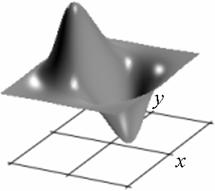
Профиль отклика оператора (15), действующего на двумерный гауссиан представлен на рис. 1.
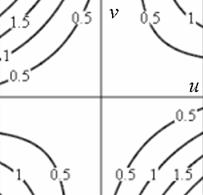
а) б)
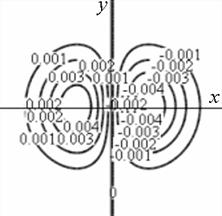
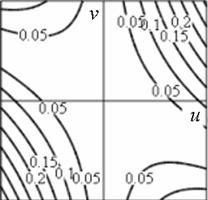
Рис. 1. Профиль отклика оператора Кирша, действующего на гауссиан (а) и соответствующая контурная карта (б) профиля.
На рис. 2. представлено тестовое изображение fi,j размером P = Q = 128 и глубиной 8 бит -а), отклик gi,j оператора Кирша -б) и канонического оператора Кирша gci,j -в)
а) б) в)
Рис. 2. Тестовое изображение fi,j (а) отклик оператора Кирша gi,j (б) и отклик канонического оператора Кирша gci,j (б).
Относительную разность откликов можно оценить, как
где стандартное отклонение
![]() откликов g и gc равно
откликов g и gc равно
а амплитуда полусуммы откликов
В случае тестового изображения (Рис. 2.)
Amp = 4049,
![]() и Dev = 0,038 (21)
и Dev = 0,038 (21)
Таким образом достаточно малая относительная разность откликов Dev, что наглядно видно из сопоставления рис. 2 (б) и (в), позволяет равноправно использовать как исходные, так и канонические маски.
В табл. 1 приведены результаты вычислений канонических аналогов для известных масок, широко применяемых при обработке изображений. Здесь же даны величины Dev для конкретного изображения рис. 2.
Сравнение исходной и канонической форм масок
|
Название |
Маска |
Характеристика |
Каноническая маска |
Dev |
|
Кирша (0°) |
|
|
|
0,038 |
|
Кирша (45°) |
|
|
|
0,023 |
|
Робинсона (0°) |
|
|
|
0,036 |
|
Робинсона (45°) |
|
|
|
0,024 |
|
Собела |
|
|
|
0,026 |
|
Превитта (0°) |
|
|
|
0,036 |
|
Превитта (45°) |
|
|
|
0,022 |
|
Робертса-1 (0°) |
|
|
|
0,039 |
|
Лапласа-2 |
|
|
|
0,028 |
|
Градиент по x и y |
|
|
|
0,052 |
|
Blur |
|
|
|
0,018 |
|
Маска сглаживания № 2 |
|
|
|
0,016 |
|
Маска сглаживания № 3 |
|
|
|
0,01 |
Маски
Робертса-1 (45°):
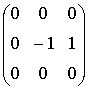 , Робертса-2:
, Робертса-2:
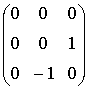 ,
Лапласа-1:
,
Лапласа-1:
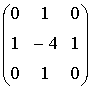 ,
,
градиент по x:
 , градиент по y:
, градиент по y:
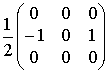 - сами
являются каноническими
- сами
являются каноническими
Из табл. 1. видно, что канонические маски Собела и Превитта (0°) с точностью до постоянных множителей совпадают с маской градиента по x (назовем их эквивалентными) Каноническая маска Превитта (45°) эквивалентна канонической маске градиента по x и y, маски Лаплас-1 и Лаплас-2 также эквивалентны.
Эти примеры показывают, что каждой канонической маске может соответствовать множество эквивалентных неканонических масок (образуя класс эквивалентности).
4. Определение АЧХ эквивалентного фильтра
Преобразование Фурье для изображения f(x, y)
является примером глобальной
обработки изображения (здесь и далее
![]() ). Над спектром F(u,v)
можно осуществить фильтрацию в частотной области с помощью некоторого фильтра Ф(u,
v), а после обратного преобразования Фурье -
получить обработанное изображение.
). Над спектром F(u,v)
можно осуществить фильтрацию в частотной области с помощью некоторого фильтра Ф(u,
v), а после обратного преобразования Фурье -
получить обработанное изображение.
Согласно теореме Бореля [2] свертка (5) эквивалентна произведению в частотной области:
где ![]() - обратное преобразование Фурье.
- обратное преобразование Фурье.
Таким образом локальная обработка (5) эквивалентна некоторой глобальной фильтрации и наоборот.
Сформулируем задачу определения амплитудно – частотной характеристики (АЧХ) фильтра, эквивалентного заданной маске. Во избежание терминологической путаницы назовем такие фильтры ассоциированными со своими масками.
Для этого в качестве f(x, y) воспользуемся двумерным гауссианом G(x,y) с достаточно малым значением дисперсии s:
Преобразование Фурье от (24) есть
Известно [3], что при s ® 0 (24) приближается к d - функции Дирака, а (25) - к спектру белого шума, что объясняет наш выбор.
Если вычислить Фурье – спектр отклика g(x, y), полученного в результате действия дифференциального оператора
то после деления его на (25), в пределе s ® 0 получим АЧХ соответствующего частотного фильтра:
Более строгое определение АЧХ можно дать следующим образом.
Известно [4], что для
![]() (пространство обобщенных функций)
(пространство обобщенных функций)
a - порядок дифференциального оператора. В частности,
![]() , (29)
, (29)
где d - дельта – функция Дирака. Тогда по теореме о свертке
С другой стороны,
Тогда АЧХ, как отношение спектров
g и f (там, где определено
сокращение на![]() ),
равна
),
равна
Была проделана
работа по прямому вычислению АЧХ известных масок по уравнению (32), где в
качестве
![]() -
функции использовался гауссиан (24) с последующим переходом к пределу
-
функции использовался гауссиан (24) с последующим переходом к пределу
![]() . В результате
громоздких вычислений в итоге получаются весьма простые и наглядные
аналитические выражения для АЧХ. В Приложении 2
приведены таблицы, в которых собраны вместе исходный вид маски, соответствующий
дифференциальный оператор, матрица характеристики, инварианты, канонические
параметры и тип конического сечения, уравнение АЧХ и профили
. В результате
громоздких вычислений в итоге получаются весьма простые и наглядные
аналитические выражения для АЧХ. В Приложении 2
приведены таблицы, в которых собраны вместе исходный вид маски, соответствующий
дифференциальный оператор, матрица характеристики, инварианты, канонические
параметры и тип конического сечения, уравнение АЧХ и профили
![]() и АЧХ. Там, где вид
этих профилей нетривиален, приводятся их контурные карты. Заметим, что профили
производных из таблиц Приложения 2 представляют
собой модельные образы
и АЧХ. Там, где вид
этих профилей нетривиален, приводятся их контурные карты. Заметим, что профили
производных из таблиц Приложения 2 представляют
собой модельные образы
![]() для случая, когда d - функция аппроксимируется
гауссианом с конечной (но достаточно малой) величиной s.
для случая, когда d - функция аппроксимируется
гауссианом с конечной (но достаточно малой) величиной s.
5. Сопоставление уравнений характеристик и АЧХ
В табл. 2. сведены вместе уравнения характеристик однородных масок и АЧХ ассоциированных фильтров.
Таблица
2.
Сравнение характеристик масок и АЧХ ассоциированных
фильтров
|
Наименование оператора |
Характеристика |
АЧХ |
|
Кирша (0°) |
|
|
|
Кирша (45°) |
|
|
|
Робинсона (0°) |
|
|
|
Робинсона (45°) |
|
|
|
Собела |
|
|
|
Превитта (0°) |
|
|
|
Превитта (45°) |
|
|
|
Робертса-1 (0°) |
|
|
|
Робертса-1 (45°) |
|
|
|
Робертса-2 |
|
|
|
Лапласа-1 |
|
|
|
Лапласа-3 |
|
|
|
Градиент по x |
|
|
|
Градиент по y |
|
|
|
Градиент по x и y |
|
|
Очевидно, что
АЧХ эквивалентных масок также эквивалентны. Кроме того можно видеть, что
формальной заменой
![]() из уравнений характеристик получаются
уравнения АЧХ, что составляет содержание следующей теоремы:
из уравнений характеристик получаются
уравнения АЧХ, что составляет содержание следующей теоремы:
Теорема 2
АЧХ ассоциированного фильтра для однородной маски 3´3 определяется выражением:
Дополнительного исследования требует случай неоднородных масок.
Например, маске сглаживания Blur
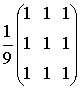 соответствует дифференциальный
оператор
соответствует дифференциальный
оператор
![]() Прямое
вычисление АЧХ дает
Прямое
вычисление АЧХ дает
где
 - приближение 2-мерной d - функции.
- приближение 2-мерной d - функции.
Тогда
Именно эти значения и приведены в таблицах Приложения 2. Дельта – особенность в начале координат функции АЧХ обеспечивает выделение постоянной составляющей в спектре изображения, однако квадратичные по u и v слагаемые дают некоторый вклад верхних пространственных частот в результирующее изображение.
Эти результаты позволяют обобщить теорему 2 на случай масок с ненулевой суммой элементов, а именно:
Теорема 3
АЧХ ассоциированного фильтра для маски 3´3 определяется выражением:
6. Заключение
Предлагаемая
теория неадаптивных масок
![]() не завершена в настоящее время, поэтому
предполагается вынести в следующую статью вопросы построения масок общего
положения, обращенных масок, исследование групповых свойств масок. Разумеется,
будут предприниматься попытки доказательства сформулированных теорем, а также в
более широком плане исследоваться область практических приложений тории.
не завершена в настоящее время, поэтому
предполагается вынести в следующую статью вопросы построения масок общего
положения, обращенных масок, исследование групповых свойств масок. Разумеется,
будут предприниматься попытки доказательства сформулированных теорем, а также в
более широком плане исследоваться область практических приложений тории.
ПРИЛОЖЕНИЕ 1
Классификация конических сечений
Уравнение конического сечения можно записать как
![]() (П1.1)
(П1.1)
Инварианты конических сечений относительно движений системы координат
![]()
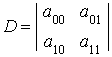
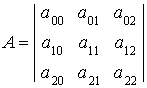 (П.1.2)
(П.1.2)
полуинвариант (только относительно вращений)
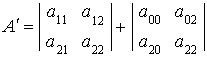 (П1.3)
(П1.3)
Классификация кривых по значениям инвариантов сведена в табл. П.1.1
.
Таблица П.1.1.
|
|
А ¹ 0 |
А = 0 |
|||
|
D ¹ 0 |
D > 0 |
|
Эллипс |
Действительная точка пересечения двух мнимых прямых |
|
|
|
Мнимый эллипс |
||||
|
D < 0 |
Гипербола |
Пара действительных пересекающихся прямых |
|||
|
D = 0 |
Парабола |
|
Пара мнимых параллельных прямых |
||
|
|
Пара действительных параллельных прямых |
||||
|
|
Одна действительная прямая |
||||
Собственные значения l12 матрицы
![]() находятся, как корни
характеристического уравнения
находятся, как корни
характеристического уравнения
![]() (П.1.4)
(П.1.4)
Координаты центра кривой

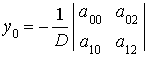 (П.1.5)
(П.1.5)
Угол главной оси кривой относительно Ox
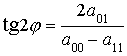 (П.1.6)
(П.1.6)
Канонические параметры для эллипса
![]() Þ
Þ
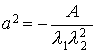
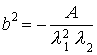
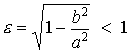 (П.1.7)
(П.1.7)
Канонические параметры для гиперболы
![]() Þ
Þ

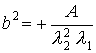
 (П.1.8)
(П.1.8)
Параметр p параболы
![]() Þ
Þ
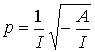 (П.1.9)
(П.1.9)
Параметры p эллипса и гиперболы
![]() (П.1.10)
(П.1.10)
ПРИЛОЖЕНИЕ 2
Некоторые свойства неадаптивных масок
![]()
Единица
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
0 |
0 |
0 |
- |
- |
- |
- |
|
Действительная прямая |
|||||||||
|
|
|
||||||||
|
Профиль производной |
|
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
K(u,v) = 1 |
|||||||||
Примечание:
-пояснения к терминам - в тексте
-обозначения канонических параметров характеристики и ее инвариантов соответствуют Приложению 1
Градиент по x
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
-1 |
0 |
0 |
- |
- |
- |
- |
|
Действительная прямая |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Градиент по y
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
-1 |
0 |
0 |
- |
- |
- |
- |
|
Действительная прямая |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Градиент по x и y
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
-2 |
0 |
0 |
- |
- |
- |
- |
|
Действительная прямая |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Лапласа-1
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
2 |
1 |
0 |
0 |
1 |
1 |
- |
- |
- |
- |
|
Действительная точка пересечения двух мнимых прямых |
|||||||||
|
|
|
||||||||
|
Профиль производной |
|
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Лапласа-2
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
6 |
9 |
0 |
0 |
3 |
3 |
- |
- |
- |
- |
|
Действительная точка пересечения двух мнимых прямых |
|||||||||
|
|
|
||||||||
|
Профиль производной |
|
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Лапласа-3
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
0 |
0 |
0 |
- |
- |
- |
- |
|
- |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Собела
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
-16 |
0 |
0 |
- |
- |
- |
- |
|
Действительная прямая |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Превитта (0°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
-9 |
0 |
0 |
- |
- |
- |
- |
|
Действительная прямая |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Превитта (45°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
0 |
0 |
-8 |
0 |
0 |
- |
- |
- |
- |
|
Действительная прямая |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Робертса-1 (0°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
1 |
0 |
0 |
|
0 |
1 |
- |
- |
- |
- |
|
Две параллельных прямых (135°) |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Робертса-1 (45°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
|
0 |
0 |
|
0 |
|
- |
- |
- |
- |
|
Две параллельных прямых (0°) |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Робертса-2
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
0 |
|
0 |
|
|
|
- |
- |
- |
- |
|
Две пересекающиеся прямые в точке (-1, -1) |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Робинсона (0°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
1 |
0 |
-9 |
-9 |
0 |
1 |
- |
- |
3 |
- |
|
Парабола |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
Контурная карта модуля АЧХ |
||||||||
Оператор Робинсона (45°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
2 |
0 |
-16 |
-8 |
0 |
2 |
- |
- |
4 |
- |
|
Парабола, 225° |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Оператор Кирша (0°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
2 |
-3 |
144 |
-144 |
-1 |
3 |
16 |
48 |
144 |
- |
|
Гипербола |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
Контурная карта модуля АЧХ |
||||||||
Оператор Кирша (45°)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
-2 |
-15 |
640 |
-128 |
-5 |
3 |
|
|
|
- |
|
Гипербола, ось 225°, центр с координатами |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|
||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
Контурная карта модуля АЧХ |
||||||||
Маска сглаживания 1 (Blur)
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
2/3 |
1/9 |
1/9 |
2/3 |
1/3 |
1/3 |
- |
- |
- |
- |
|
Мнимый эллипс |
|||||||||
|
|
|
||||||||
|
Профиль производной |
|
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Маска сглаживания 2
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
3/5 |
9/100 |
9/100 |
3/5 |
3/10 |
3/10 |
- |
- |
- |
- |
|
Мнимый эллипс |
|||||||||
|
|
|
||||||||
|
Профиль производной |
|
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Маска сглаживания 3
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
1/2 |
1/16 |
1/16 |
1/2 |
1/4 |
1/4 |
- |
- |
- |
- |
|
Мнимый эллипс |
|||||||||
|
|
|
||||||||
|
Профиль производной |
|
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
|
||||||||
Без названия
|
Маска |
Дифференциальный оператор |
Характеристическая матрица |
|||||||
|
|
|
|
|||||||
|
Инварианты |
Собственные значения |
Канонические параметры |
|||||||
|
I |
D |
A |
A’ |
l1 |
l2 |
a |
b |
P |
e |
|
1/2 |
-1/4 |
0 |
-5/4 |
|
- |
- |
- |
- |
|
|
Две пересекающиеся
прямые с центром в (-2, 1), угол |
|||||||||
|
|
|
||||||||
|
Профиль производной |
Контурная карта |
||||||||
|
Амплитудно – частотная характеристика фильтра |
|||||||||
|
|
|||||||||
|
|
|
||||||||
|
Модуль АЧХ фильтра |
Контурная карта модуля АЧХ |
||||||||
ЛИТЕРАТУРА
1. Бакут П.А., Колмогоров. - Зарубежная радиоэлектроника, 1987, № 10 с.25.
2. http://www.khoral.com/contrib/contrib/dip2001/index.html
3. Г. Корн, Т. Корн. Справочник по математике //М.: "Наука", 1974, 831 с.
4. В.С. Владимиров Обобщенные функции в математической физике.//М.: "Наука", 1979, 318 с.
Автор:
Семенов Станислав Иванович, Отдел медицинской физики, информатики и дозиметрии Владимирского областного онкологического диспансера, e-mail: stas@onko.elcom.ru
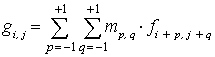
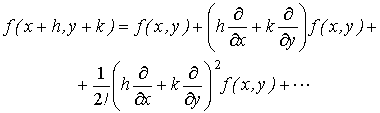
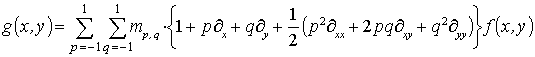 (3)
(3)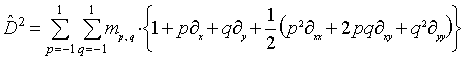 (6)
(6)
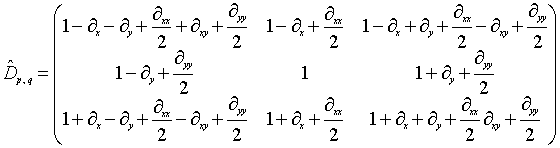 , (10)
, (10)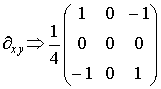 ,
,
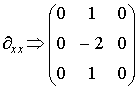 ,
,
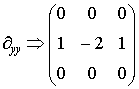 (11)
(11)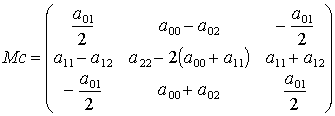 (12)
(12)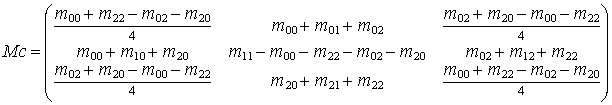
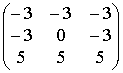 (14)
(14)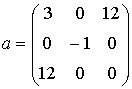 (16)
(16) (17)
(17)




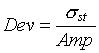 ,
(18)
,
(18) , (19)
, (19)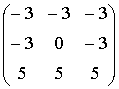








 (22)
(22) (24)
(24)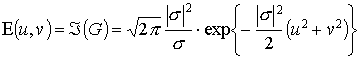 (25)
(25)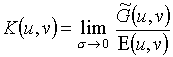
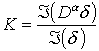 (32)
(32)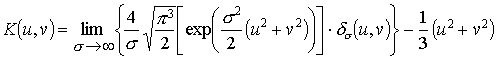 , (34)
, (34)