|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2003 |
|
Синтез компактных трансформаторов сопротивлений на основе шлейфов с плавно изменяющийся функцией волнового сопротивления
А. Н. Ануфриев, И. Н. Салий ; e-mail: alexmym@yandex.ru
Саратовский государственный университет
Получена 04 сентября 2003 г.
Представлены оптимальные конструкции трансформаторов активных сопротивлений (ТС) на отрезках однородных линий передачи (ЛП) с нерегулярными шлейфами (НШ). Проведен сравнительный анализ полосы согласования, коэффициента отражения в полосе и длины ТС с НШ и ТС с регулярными шлейфами (РШ) . Показано, что рассмотренные конструкции имеют меньший коэффициент отражения в полосе согласования и, что наиболее важно, длина НШ меньше длины РШ. Различие в длинах уменьшается с увеличением количества секций ТС.
1. Введение.
Одним из базовых элементов пассивных устройств, применяемых в современной технике СВЧ, является шлейф – отрезок ЛП, параллельно или последовательно включенный в ЛП. В ТС шлейф играет роль резонатора и обычно разомкнут или короткозамкнут на конце. Основной характеристикой, определяющей его свойства как резонатора, включенного в ЛП, является спектр собственных частот, резонансных и противорезонансных. Резонансные частоты соответствуют полюсам входного сопротивления, противорезонансные - нулям.
Простейшим вариантом шлейфа-резонатора является отрезок регулярной ЛП. Его спектр представляет собой эквидистантную последовательность чередующихся резонансных и противорезонансных частот. В более сложном варианте сам резонатор может иметь шлейфную структуру. Спектр собственных частот такой системы имеет неэквидистантный характер.
Основная масса исследованных к настоящему времени структур широкополосных ТС представляет собой каскадное соединение однородных элементов: шлейфов и отрезков соединительных ЛП. [1-5].
Широкие возможности реализации колебательных систем, и в частности ТС, с заданной последовательностью собственных частот представляют нерегулярные ЛП. Одной из структур данного типа, получившей широкое распространение, является резонатор на основе плавных ЛП радиального типа [6–8]. Он применяется в полосковых и микрополосковых устройствах в качестве шлейфов, имеющих близкое к нулю значение входного сопротивления в широком диапазоне частот. Впервые радиальный резонатор был проанализирован Виндингом в приближении Т-волн [6].
Однако, как показали экспериментальные исследования [7], метод анализа предложенный Виндингом становится неточным в области высоких частот, а также при больших диэлектрических проницаемостях материала подложки.
Для проектирования ТС (и других
пассивных СВЧ устройств) с НШ перспективным является использование нового типа
нерегулярных ЛП – канонической нерегулярной линии передачи (КНЛП) [9,10]. ФВС
КНЛП, является трех параметрической, помимо величины волнового сопротивления в
начале отрезка определяется перепадом численных значений R функции и перепадом значений ее
производной между концевыми точками отрезка. При изменении параметров ![]() ,
,![]() ФВС принимает различные частные
формы, как известные, так и новые. Важно, что переход между этими типами НЛП
происходит непрерывным образом вместе с изменением параметров
ФВС принимает различные частные
формы, как известные, так и новые. Важно, что переход между этими типами НЛП
происходит непрерывным образом вместе с изменением параметров![]() ,
,![]() .
.
2. Постановка задачи.
Цель данной работы может быть сформулирована следующим образом: отыскание наиболее компактных конструкций ТС со шлейфами при заданном коэффициенте отражения в полосе. Математической моделью при параметрической оптимизации является модель КНЛП [9,10], а в качестве начального приближения выбираются параметры конструкции ТС на РШ (данный выбор оправдан тем, что регулярные ЛП являются частным случаем КНЛП), предложенные в [1] и заявленные в обзоре [11], как самые компактные ТС с РШ исследованные до настоящего времени.
При проведении анализа конструкций ТС имеют место следующие допущения:
1. ТС состоит из каскадно-включенных отрезков ЛП с параллельными разомкнутыми шлейфами. Связанные линии не рассматриваются.
2. Расчет проводится в приближении Т-волн.
3. Возможные искажения поля, появляющиеся в месте соединения двух ЛП с различными волновыми сопротивлениями не учитывается.
4. Входное сопротивление согласуемых линий вещественно и не зависит от частоты.
3. Каноническая нерегулярная линия передач.
Для ФВС КНЛП найдены
точные решения ДУ в форме аналитических соотношений для матричных параметров
эквивалентного четырехполюсника отрезка КНЛП длинной l и волновыми сопротивлениями в
концевых точках ![]() ,
являющиеся его математической моделью [9].
,
являющиеся его математической моделью [9].
![]() ;
;
![]() ,
,
![]() .
.
Здесь величина b, определяемая равенством
имеет смысл постоянной распространения в линии.
так называемая функция местных отражений.
где ![]() -перепад функции волнового сопротивления,
-перепад функции волнового сопротивления,
к – вещественная константа, непрерывное изменение которой приводит к переходу от одной частной зависимости r(z) к другой, и поэтому называемая коэффициентом формы КНЛП..
На основании (3) функции волнового сопротивления имеет вид:
Выражения (1) содержат только элементарные функции и поэтому удобны для решения практических задач синтеза микроволновых устройств методами параметрической оптимизации.
4.Математическая модель трансформатора сопротивлений с нерегулярными шлейфами.
Матрица передачи параллельного шлейфа имеет вид:
где ![]() есть входная проводимость разомкнутого шлейфа.
есть входная проводимость разомкнутого шлейфа.
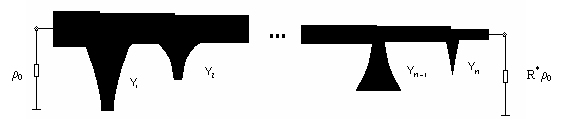
Рис. 1 Трансформатор сопротивлений на отрезках
регулярных линий с нерегулярными шлейфами
Результирующая матица передачи n каскадного ТС с НШ, изображенного на рис.1 есть:
Основным электрическим параметром, характеризующим ТС, является коэффициент отражения Г. Коэффициент отражения для ТС определяется через элементы матрицы передачи на основе соотношения [12]:
Математически задача оптимизации ТС (Чебышевская аппроксимация) формулируется следующим образом [12]:
где q1,q2
соответствуют нижней и верхней границам рабочей полосы частот. Компонентами
вектора являются длина, ![]() ,
, ![]() и коэффициент формы k.
и коэффициент формы k.
5. Анализ результатов.
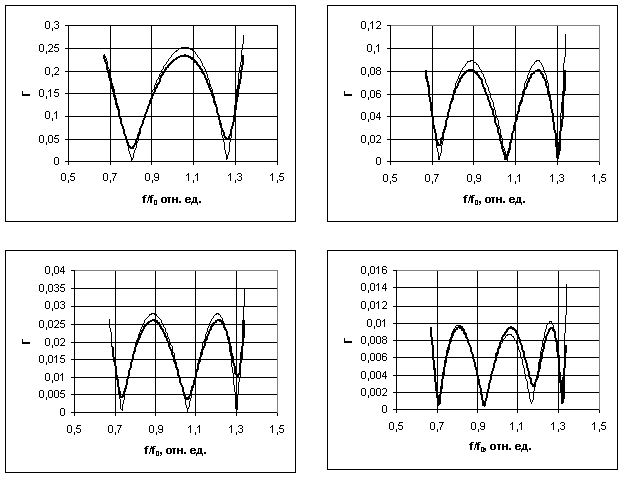
Параметры конструкций ТС с НШ представлены в таблице 1, а их амплитудно-частотные характеристики, полученные в результате оптимизации, представлены на рисунке 2 , на основе которых можно сделать вывод, что ТС на НШ имеет меньший коэффициент отражения в полосе согласования по сравнению с ТС на РШ и, что наиболее важно, длина НШ меньше длины РШ. Разница между регулярными и нерегулярными шлейфами растет с увеличением количества секций ТС (таблица 1).
То есть, в результате анализа ТС на НШ показано, что они имеют наименьшие габариты из всех ТС, известных нам к настоящему времени. Данная особенность делает их наиболее перспективным согласующим устройством при разработке узлов и элементов твердотельных приборов, и особенно широкополосных МИС СВЧ.
а) б)
с) д)
Рис. 2 Амплитудно-частотные характеристики ТС с НШ (——) и с ОШ (▬▬)
а) N=4, R*=2; б) N=6; R*=7; c) N=6, R*=2; д) N=8; R*=2
|
|
ТС с РШ |
|
|
ТС с НШ |
|
|
||
|
|
|
N=4 |
, R*=2 |
|
|
|
||
|
|
r(0)=r(l) |
l/l |
r(0) |
r(l) |
l/l |
k |
||
|
Линия 1 |
2.3775 |
0.0625 |
2.3775 |
2.3775 |
0.0625 |
0.0000 |
||
|
Шлейф 1 |
0.5926 |
0.0625 |
0.1515 |
0.4925 |
0.0304 |
0.0334 |
||
|
Линия 2 |
4.2162 |
0.0625 |
4.2162 |
4.2162 |
0.0625 |
0.0000 |
||
|
Шлейф 2 |
1.0509 |
0.0625 |
0.178 |
0.8599 |
0.0076 |
0.1101 |
||
|
Гmax |
0.0818 |
0.0752 |
||||||
|
|
|
N=6 |
, R*=2 |
|
|
|
||
|
Линия 1 |
1.9950 |
0.0625 |
1.9950 |
1.9950 |
0.0625 |
0.0000 |
||
|
Шлейф 1 |
0.5558 |
0.0625 |
0.3004 |
0.4847 |
0.0440 |
0.0220 |
||
|
Линия 2 |
4.0552 |
0.0625 |
4.0552 |
4.0552 |
0.0625 |
0.0000 |
||
|
Шлейф 2 |
0.5615 |
0.0625 |
0.3003 |
0.4874 |
0.0436 |
0.0236 |
||
|
Линия 3 |
4.6008 |
0.0625 |
4.6008 |
4.6008 |
0.0625 |
0.0000 |
||
|
Шлейф 3 |
1.2819 |
0.0625 |
0.3723 |
1.0689 |
0.0309 |
0.1501 |
||
|
Гmax |
0.0353 |
0.0261 |
||||||
|
|
|
N=8 |
, R*=2 |
|
|
|
||
|
Линия 1 |
1.7272 |
0.0625 |
1.7272 |
1.7272 |
0.0625 |
0.0000 |
||
|
Шлейф 1 |
0.5640 |
0.0625 |
0.4866 |
0.5379 |
0.0569 |
0.0083 |
||
|
Линия 2 |
3.6560 |
0.0625 |
3.6560 |
3.6560 |
0.0625 |
0.0000 |
||
|
Шлейф 2 |
0.4851 |
0.0625 |
0.4382 |
0.4681 |
0.0584 |
0.0042 |
||
|
Линия 3 |
4.6702 |
0.0625 |
4.6702 |
4.6702 |
0.0625 |
0.0000 |
||
|
Шлейф 3 |
0.6192 |
0.0625 |
0.5869 |
0.6067 |
0.0602 |
0.0043 |
||
|
Линия 4 |
4.7060 |
0.0625 |
4.7060 |
4.7060 |
0.0625 |
0.0000 |
||
|
Шлейф 4 |
1.5390 |
0.0625 |
1.5556 |
1.5442 |
0.0629 |
-0.0054 |
||
|
Гmax |
0.0145 |
0.0095 |
||||||
|
|
|
N=8 |
, R*=7 |
|
|
|
||
|
Линия 1 |
2.3524 |
0.0625 |
2.3524 |
2.3524 |
0.0625 |
0.0000 |
||
|
Шлейф 1 |
0.5819 |
0.0625 |
0.3872 |
0.4800 |
0.0237 |
0.0389 |
||
|
Линия 2 |
5.6939 |
0.0625 |
5.6939 |
5.6939 |
0.0625 |
0.0000 |
||
|
Шлейф 2 |
0.7618 |
0.0625 |
0.3498 |
0.6555 |
0.0414 |
0.0494 |
||
|
Линия 3 |
10.4170 |
0.0625 |
10.4170 |
10.4170 |
0.0625 |
0.0000 |
||
|
Шлейф 3 |
1.3934 |
0.0625 |
0.6310 |
1.1964 |
0.0400 |
0.1553 |
||
|
Линия 4 |
15.0046 |
0.0625 |
15.0046 |
15.0046 |
0.0625 |
0.0000 |
||
|
Шлейф 4 |
3.7147 |
0.0625 |
1.7856 |
3.1946 |
0.0355 |
1.0141 |
||
|
Гmax |
0.0309 |
0.0264 |
||||||
|
* r(0), r(l) - нормированные к волновому сопротивлению r0 подводящей линии |
|
|||||||
|
* R* - Rн/r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Van der Walt P.W. Shot-step-stub Chebyshev impedance trsnsformers //IEEE Trans. – 1986. – V.MTT-34, №8. – P.863–868.
2. Mayer K. Syntese von optimalen mehrstufigen l/4 – transformatoren mit stichleitungen// AEU.- 1971. – B.25, h.2. – S.61–68.
3. Podcameni A., Conrado L.F. Broadbanding the l/4 transformer using two parallel stubs// Electron. Lett. – 1981. – V.17, №11. – P. 372–374.
4. Matthaei G.L. Short-step-stub Chebyshev impedance transformers// IEEE Trans. – 1966. – V.MTT-14, №8, - P.372–383.
5. Drozd M. Joines W. Using parallel resonators to create improved maximally flat quarter-wavelength transformer impedance-matching networks// IEEE Trans. – 1999, V.MTT-47, №2, - P.132-141.
6. Vinding J.P. Radial line stubs as elements in stripline circuits// NEREM Record. – 1967. - P.108-109.
7. Gao Bao-xin, Chen Zhao-qing A mode-matching method for analysis microstrip radial stubs// 17 Microwave Conf., Kome, 7 – 11 Sept., 1987: Conf. Proc. – Tunbridge Wells [1987],. – P.923-926.
8. Atwater H.A. Microstrip reactive circuit elements// IEEE Trans. – 1983. – V.MTT-31, №6. – P.488-491.
9. Салий И.Н. Канонические нерегулярные линии передачи и их эквивалентные представления //Лекции по электронике СВЧ и радиофизике: 8-я зимняя шк.- семинар инженеров. Книга 4.– Саратов: Изд-во СГУ, 1989. – С. 73-80.
10. Салий И.Н. Обобщенная нерегулярная линия передачи и разработка на ее основе новых функциональных элементов и узлов твердотельной электроники //Моделирование и проектирование приборов и систем микро- и наноэлектроники: Межвуз. сб. – М.: Изд-во МГИЭТ(ТУ), 1994. – С. 15-29.
11. Богданов А.М, Мещанов В.П., Скородумова Н.Г. Шлейфные устройства СВЧ на основе линий передач с Т-волнами: Обзоры по электронной технике. Сер. 1, Электроника СВЧ. – М.: ЦНИИИ «Электроника», 1988. - Вып. 7 (1675). – 73 с.
12. Мещанов В.П., Тупикин В.Д., Чернышев С.Л. Коаксиальные пассивные устройства. - Саратов, СГУ, 1993. - 413 с.
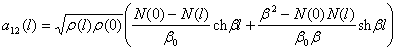 ;
;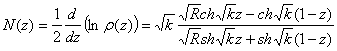
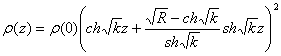 (4)
(4)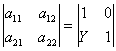 (5)
(5)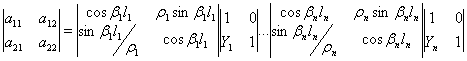 (6)
(6)