Институт радиотехники и электроники РАН

 

Получена 19 сентября 2005 г.

 

В статье рассмотрена задача нахождения коэффициента преломления ограниченной неоднородной среды с осевой симметрией по заданной фазовой характеристике прошедшего через нее поля. Предложены и исследованы две аналитические методики получения решения в приближении геометрической оптики. Первая из них, основана на использовании разложения всех параметров задачи по степеням отношения расстояния от оси системы к толщине среды на оси. Вторая – на использовании слоистой модели неоднородной среды, причем внутри каждого слоя коэффициент преломления полагается постоянным. Первая методика может применяться для градиентных сред, а вторая как для слоистых, так и градиентных сред (при использовании достаточно большого количества слоев).

 

 

          В задачах диагностики неоднородных сред, при синтезе градиентных или слоистых линзовых антенн [1,2] необходимо найти профиль  коэффициента преломления. В данной работе рассматриваются задача определения профиля коэффициента преломления  осесимметричной ограниченной неоднородной среды по фазовой характеристике выходного фронта. Падающий лучевой фронт здесь и далее предполагается сферическим с источником на оси симметрии среды.

В цилиндрической системе координат, связанной с осью симметрии среды  z ,  среда характеризуется тремя функциональными зависимостями: функция z=f(r) , описывающая первую границу среды (на которую падает сферический фронт),  z=j(r) – функция, описывающая вторую границу среды, и n(r) –коэффициент преломления среды.

 В силу осевой симметрии задачи здесь и далее достаточно рассмотреть ход лучей в одной из плоскостей, проходящих через ось симметрии среды (рис.1). Уравнение семейства лучей в этой плоскости имеет вид [1]

 

                                                                                    (1)

 

         где а – лучевой параметр, n(y) – коэффициент преломления,  f(y)и j(у) – формы сечения поверхностей среды. Здесь и далее осевая толщина среды принята за 1.

 

Рис. 1

        

Из уравнения лучей (1) получаем соотношение

          

                                                                          (2)

в случае, когда траектория луча монотонна и

 

                                                            (2a)

 

в случае, когда траектория луча немонотонна. Верхний предел р  в последних двух интегралах есть точка максимума луча. При у=р знаменатель в подынтегральных функциях обращается в 0.

         Закон преломления на левой границе связывает углы падения и преломления:

 

                                                                                     (3) 

 

где d₁=arctg(1/f¢(y₁) – угол наклона касательной к поверхности в точке у₁ к оси Ох, - угол наклона касательной к преломленному лучу в точке у_1, q₁- угол, образуемый лучом, выходящем из источника с осью Ох (рис.1) С помощью алгебраических преобразований соотношение (3) можно привести к виду

 

                                                                               (4)

 

Аналогично из закона преломления на правой границе можно получить соотношение

 

                                                                                       (5)

 

         Предполагается, что выходящий лучевой фронт удовлетворяет закону:

 

                                                                                                                             (6)

где q₂ – угол наклона выходящего луча,  q₂ >0  когда выходящий луч пересекает ось Ох справа от границы среды, b(у) – некоторая заданная гладкая функция, удовлетворяющая условию b(0)=0.

         Постановка задачи состоит в нахождении n(y), удовлетворяющего интегральному уравнению (2)  (или 2а) и условиям (4), (5), (6) для всех лучей, прошедших через среду, причем f(y) и j(у) предполагаются заданными. Будем также предполагать, что выходящий лучевой фронт является регулярным (не образует каустик) и функция у(х), описывающая уравнение любого луча внутри линзы имеет не более одного максимума.

         Будем использовать две методики решения задачи. В первой методике как и работе [2] решение ищется в виде разложения в ряд по четным степеням у. Вторая методика использует слоистую модель непрерывной среды, причем внутри каждого слоя коэффициент преломления предполагается постоянным. Сначала будем искать решение, используя первую методику.  Для этого представим

 

 ,  ,                                         (7)

 

где  n_o²=n²(0) – задано, коэффициенты f_2k, j_2k – заданы, с_2k (k=1,2,3,…) – неизвестные коэффициенты, подлежащие определению. В данной работе мы ограничимся случаем  среды с с₂>0 (n(y) в центре образует локальный максимум).

         Соотношение (6), описывающее выходящий лучевой фронт, представим в виде:

 

                                                                                         (8)

где b_2к-1 (к=1,2,3,…) заданы.

         Преобразуем левую часть соотношения (4). Для этого представим sinq₁, cosq₁, f¢(y₁) в виде разложений по степеням у₁ :

                   ,

                  

                  

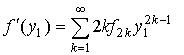где

         ,     ,     ,

         ,     .

 

Тогда

            ,

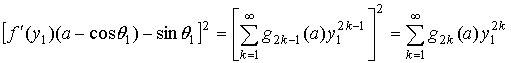где

          g₁(a)=2f₂(a-1)-n₁,  g₃(a)=4f₄(a-1)+2f₂k₂+n₃,  g₅(a)=6f₆(a-1)+4f₄k₂-2f₂k₄-n₅,  

 

         g₂=g₁²,      g₄=2g₁g₃ ,       g₆=2g₁g₅+g₃².

 

         Согласно разложениям (7), соотношение (4) можно записать в виде

                                                                                            (9)

где    a²=n_o²-a².

         Из (9) следует, что для центрального луча (у₁=0) a=n_o и a=0.

         Так как g₂+c₂>0 при всех значениях а, то можно обратить (9) относительно у₁, т.е. представить у₁² в виде ряда по степеням a²:

 

                                                                                  (10)

где

         ,   ,

        

 

         Теперь аналогичным образом преобразуем условие на правой границе (5):

 

                                                                                                                (11)

 

где    h₂=h₁²,      h₄=2h₁ h₃ ,      h₆=2h₁ h₅+h₃² ,

 

          ,     ,

 

         ,

          ,       ,      ,

          ,       .

 

         Обратим ряд (11) относительно у₂²:

 

                                                                                          (12)

где   

         ,   ,
 

        

 

         Из (10) и (12) следует

 

          ,    i=1,2                                          (13)

 

         Преобразуем уравнение (2). Используя разложение (7), подынтегральное выражение в (2) представим в следующем виде:

        

         ,                                               (14)        

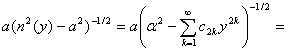
где р – корень уравнения n²(p)-a²=0 . Из представления (7) следует, что

         .

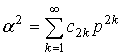Тогда имеет место разложение:

 

                                                                                (15)

 

и, следовательно,

 

         .                                                           (16)

 

Коэффициенты R_2k, Q_2k (k=0,1,2,…) выражаются через коэффициенты рядов (7) и (16). Так, первые три имеют вид

 

         R_o=a² /p², R₂=c₄+p²c₆ , R₄=c₆ ,

         Q_o=p/a ,  Q₂= -1/2p³/a³(c₄+p²c₆) ,  Q₄=3/8p⁵/a⁵(c₄+p²c₆)²-1/2p³/a³c₆ .                            (17)              

 

Используя разложение (14), интеграл в (2) можно представить в виде суммы интегралов:

 

                                                                          (18)

а интеграл в (2а)

 

                   (18а)

где   

        

Все интегралы I_2k  выражаются явно:

     ,  ,

          ,  . . .

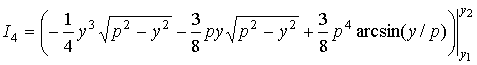Подставляя вместо у₁, у₂, р в последних формулах выражения (13), (15) и (16), заменяя arcsin(y/p) и (p²-y²)^1/2 в них формулами Тейлора с нужным числом степеней a и приводя в (18) и (18а) члены с одинаковыми степенями a, получаем :

 

             a²=n_o²-a².                                                                                 (19)

Где, для  монотонных лучей

 

          ,

 

          ,

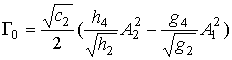          ,    ( i=1,2),

          .

 

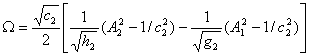И для  немонотонных лучей:

 

         

         

         

         

 

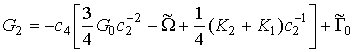
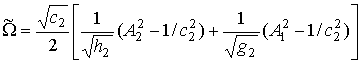
          Преобразуем теперь правую часть уравнения (2). Пусть Y(a)=j(y₂)-f(y₁). Используя разложения (7), (10) и (12) и приводя подобные члены, можно записать

 

                                                                                                                  (20)

где

                   ,   ,

                   .

          Интегральное уравнение (2) можно записать теперь в виде 

 

                                      I(a) = Y(a),                                                                                                (21)

 

 где I(a) задается рядом (19), а Y(а) – рядом (20).

          Тождество (21) выполняется при всех значениях параметра а , в том числе и при а=n_o, соответствующему центральному лучу. Приравнивая левую и правую части тождества (21), а также их производные при а=n_o получаем систему уравнений для определения c_2k:

 

                             ,

                            ,                                                                                         (22)

                            ,

                            ………………………

 

          В приведенной системе первое уравнение содержит с₂, второе уравнение содержит с₂, с₄, третье – с₂,с₄,с₆ и т.д., что определяет метод решения – сверху вниз. 

          Первое уравнение системы (22) в случае монотонных лучей имеет вид:

 

          .                                             (23)

а в случае немонотонных:

 

                                                       (23а)

Уравнения являются трансцендентными относительно с₂ и могут быть решены только численным методом. С помощью тригонометрического преобразования (23) может быть приведено к виду

 

                                                                                      (24)

а уравнение (23а) к виду

 

                                                                                       (24а)

 

где А₁ и А₂ определяются соотношениями (10) и (12).

          Второе уравнение системы (22) является линейным относительно с₄. Приведем его решение для случая монотонных лучей:

 

            ,                                             (25)

 

 где

          ,  ,

         

         

 

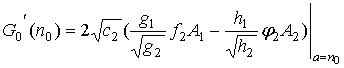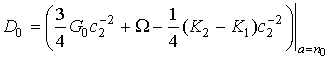
И для случая немонотонных лучей

 

                                                            (25а)

 

где

         

         

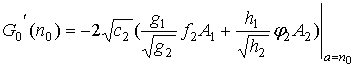
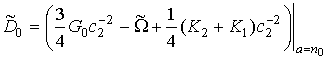
          Решая третье уравнение системы (22) (линейное относительно с₆ ), можно определить с₆ и т.д.

          Приведем пример, иллюстрирующий существование двух решений поставленной задачи в классе монотонных и немонотонных лучей. Рассмотрим среду, ограниченную двумя квадратичными поверхностями  f(y)=f₀ + f₂y²  и j(y)=f₀+1+ j₂y², при f₂=j₂=0.1, которая преобразует сферический фронт с радиусом 1 в сферический фронт радиусом 10. По приведенным формулам было найдено 2 закона изменения  n(y) – один для монотонного, а другой - для немонотонного класса лучей до четвертого члена разложения. На рисунке 2  приведены графики зависимостей n(y), кривая с цифрой 1 для монотонного класса лучей, кривая 2 – для немонотонного класса.

 

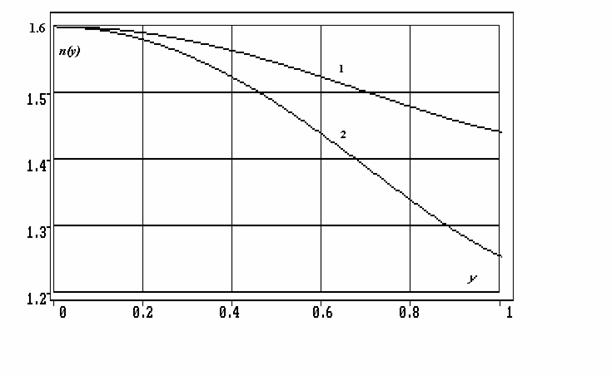
Рис.2

 

 

          Перейдем к рассмотрению другой методики. Будем искать решение n(y) в классе кусочно-постоянных функций. Сечение среды в этом случае будет представлять собой набор дискретных слоев (рис. 3) с постоянным значением n(y) внутри каждого слоя.  При рассмотрении данной методики будем предполагать, что лучи – монотонные кривые.

 

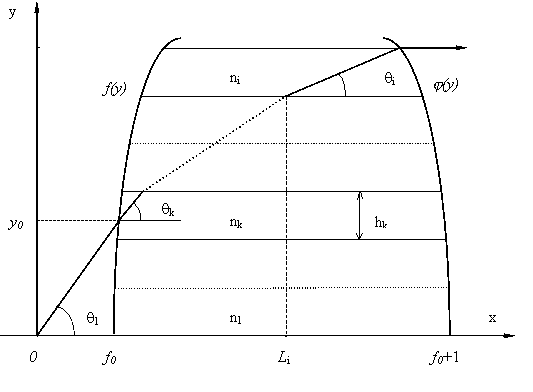
Рис.3

 

Зададим h₁ – толщину первого слоя и выберем q_о так, что луч выйдет из среды в точке у₂=h₁ . Выбором   h₁ всегда можно добиться, чтобы разность фазы этого луча и идеальной фазы была меньше заданной ошибки. Слой с параметрами h₁ и n₁=n_o будет первым слоем синтезированной среды. 

         Предположим, следуя методу математической индукции, что мы уже определили i-1 слоев, т.е. знаем n_j, h_j , j=1,…, i-1. Опишем процедуру нахождения i-го слоя, т.е. n_i, h_i.

         Рассмотрим луч, выходящий из источника под углом q₁=iq_o . Пусть слой, в который попадет этот луч имеет номер k. Будем считать, что k < i, в противном случае будем уменьшать  q₁ до тех пор, пока не станет   k <  i. Точку выхода луча из среды  будем считать второй границей искомого i-го слоя y_i+1.  Рассчитаем оптический путь луча до выхода из среды

 

          ,                                              (26)

 

где у_о-точка входа луча в среду, а q_k определяется из закона преломления на левой границе

 

         ,

 

где d=arctg(1/f¢(y_о) – угол наклона касательной к поверхности в точке пересечения луча со средой к оси Ох. S_i – отрезок луча в определяемом i – м  слое – можно найти из теоремы синусов:

 

,                                                                                                       (27) 

j_i= j(y_i) ,         ,

          .

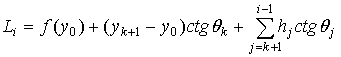L_i – абсцисса точки пересечения луча с границей i-го слоя.

         Толщины слоев предполагаются достаточно малыми, что позволяет заменить функцию j(у), описывающую правую поверхность, на кусочно-линейную

                            при y_i£ y£y_i+1.

Также с помощью линейной интерполяции выразим фазу в точке у_i+1

 

                                                                                            (28)

 

Приравнивая правые части соотношений (26) и (28) и используя равенство (27), получаем уравнение для определения q_i

        

          ,

 

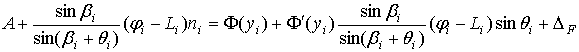где    ,

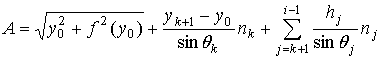         D_F – принятая погрешность фазы.

Исключением из последнего уравнения неизвестного коэффициента n_i с помощью равенства 

                    ,          где q=n_kcosq_k =n_k+1cosq_k+1=…

уравнение приводится к виду  

 

          ,

 

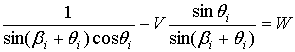где   ,   .

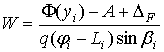         Решение последнего уравнения
        

          ,

где m определяется равенствами

          ,                 ,

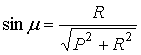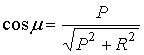         P=Wsinb_i ,  R=Wcosb_i+V ,  U=2-Wsinb_i.

 

После находим n_i в искомом слое

                                     

и высоту i-го слоя

                                       .

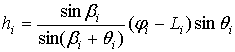Далее переходим к определению по приведенной схеме i+1 слоя и т.д.

         В качестве примера для проверки точности обеих методик использовалась градиентная среда с законом изменения коэффициента преломления как в линзе Микаэляна [1]. Первая поверхность среды предполагалась  плоской, вторая  поверхность задавалась  квадратичной функцией

 

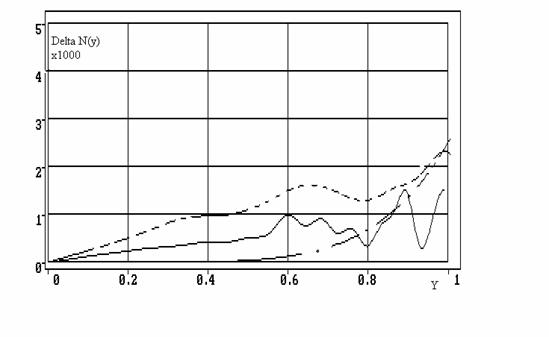
Рис.4

 

На рисунке 4 приведены кривые разности рассчитанного  коэффициента преломления  n(y) и заданного для среды с 500 слоями (пунктиром) и для среды с 1000 слоев – сплошной линией.

Штрих-пунктирной линией показана соответствующая разность, полученная с использованием формул (24)-(25). Видно, что точность восстановления коэффициента преломления с использованием степенного разложения, как и следовало ожидать, быстро падает с увеличением y. Падение точности при использовании модели слоистой среды  более медленное и имеет колебательный характер.

 

Литература.

 

1. Зелкин Е.Г., Петрова Р.Н., Линзовые антенны, М., Сов.Радио, 1974 г.

2. Венецкий А.С., Калошин В.А., Синтез градиентной линзовой антенны с осевой    симметрией и криволинейной формой преломляющих поверхностей, Радиотехника и электроника, 1997, том 42, №12, с.1452-1458.