|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2007 |
МЕТОДЫ РАВНОВЕСОВОЙ ОБРАБОТКИ ШУМОПОДОБНЫХ СИГНАЛОВ С МИНИМАЛЬНОЙ ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ
Политехнический институт
ФГОУ ВПО "Сибирский федеральный университет", г. Красноярск
Получена 19 сентября 2007 г.
Дано описание предлагаемых алгоритмов равновесовой корреляционной обработки шумоподобных сигналов с минимальной частотной манипуляцией. Показаны способы аппроксимации оптимального опорного сигнала. Представлена методика расчета коэффициентов аппроксимации оптимальных опорных сигналов. Приведены результаты статистического моделирования разработанных алгоритмов.
В перспективных радионавигационных системах (РНС) всё большее применение находят шумоподобные сигналы (ШПС) с минимальной частотной манипуляцией (МЧМ) [1,2], превосходящие традиционные фазоманипулированные (ФМ) сигналы по спектральной эффективности и другим показателям [2].
Цель работы
Целью данной работы является разработка и исследование помехоустойчивости алгоритмов равновесовой обработки шумоподобных МЧМ-сигналов.
Модель сигнала и структура устройства корреляционной обработки
Принимаемый ШПС-МЧМ может быть представлен как сумма двух ФМ-ШПС "со сдвигом" [3]:
где
– амплитуда сигнала;
– информационный сигнал:
,
– период повторения сигнала;
– центральная частота;
– начальная фаза;
и
– огибающие квадратурных ФМ-ШПС, которые определяются как
,
(2)
где
и
– элементы кодовых последовательностей, определяющих законы ФМ квадратурных ШПС. Элементы кодов
и
однозначно связаны с элементами
псевдослучайной последовательности (ПСП), определяющей закон частотной манипуляции:
– длительность элемента ПСП.
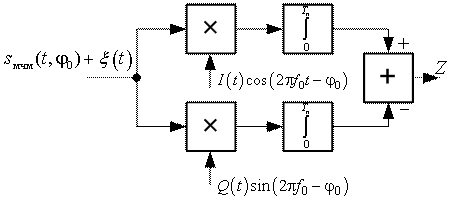
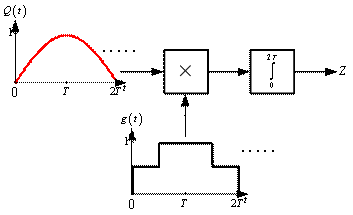
Структурная схема оптимального (по критерию максимального правдоподобия) корреляционного приёмника ШПС-МЧМ представлена на рис. 1. При дальнейших рассуждениях предполагается, что кодовая и фазовая синхронизация выполнены идеально.
Рис. 1
Оптимальный приёмник шумоподобных сигналов
с минимальной частотной манипуляцией
В отсутствие шума:
, выходная величина корреляционного приёмника определяется выражением
где
– взаимная энергия принятого ШПС-МЧМ и опорного сигнала
, который является точной копией сигнала (1), за исключением единичной амплитуды.
При наличии аддитивного белого гауссовского шума:
, выходная величина корреляционного приёмника определяется выражением
где
– шумовая компонента, с математическим ожиданием
и дисперсией
, где
– спектральная плотность шума.
В качестве критерия помехоустойчивости корреляционного приёмника ШПС-МЧМ используем отношение сигнал/шум
где
– энергия одного элемента длительностью
сигнала (1),
– число элементов на периоде повторения
,
– отношение сигнал/шум для одного элемента (
) [4].
Как видно из (7), анализ помехоустойчивости корреляционного приёмника ШПС-МЧМ можно провести с использованием критерия
.
Квазиоптимальные весовые функции
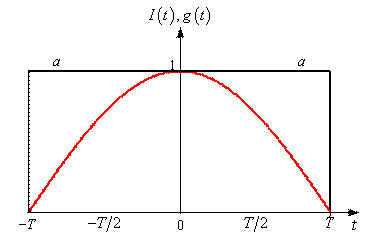
В работе предлагаются три квазиоптимальных алгоритма корреляционной обработки сигнала (1), основанные на замене оптимальных опорных сигналов (2) на их ступенчатые аппроксимации – весовые функции (ВФ). Принцип квазиоптимальной обработки элемента ШПС-МЧМ поясняется на рис. 2.
Рис. 2
Квазиоптимальная обработка элемента шумоподобного сигнала с минимальной частотной манипуляцией
Наиболее простой вариант квазиоптимальной ВФ соответствует знаковой аппроксимации сигналов (2). При этом значение ВФ определится как
. На рис. 2 – 5, красным и чёрным цветом показаны соответственно оптимальная и квазиоптимальные ВФ.
Рис. 3
Знаковая аппроксимация оптимальной весовой функции
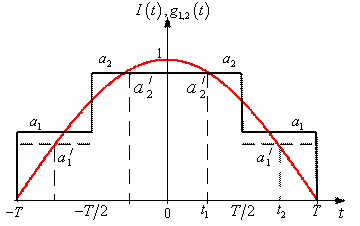
В случае двухступенчатой аппроксимации оптимальной ВФ возможны два способа расчёта весовых множителей.
Способ первый. Взвешивание оптимальной весовой функции по энергии.
Рассмотрим элемент сигналов
и
вида (2) на интервале времени
, имеем сигнальный импульс:
Задача заключается в определении коэффициентов
и
квазиоптимальной ВФ
, показанной на рис. 4.
Рис. 4
Двухступенчатая аппроксимация оптимальной весовой функции
Энергия
-го элемента (
) длительностью
сигнального импульса (8) определяется соотношением:
тогда при аппроксимации сигнального импульса (8) двухступенчатой, кусочно-заданной ВФ
, энергия
-го элемента
где
– искомые коэффициенты. Из (10) видно, что
Определим коэффициенты аппроксимации:
выполняя интегрирование в числителе и знаменателе в (12) с учетом того, что
, имеем:
Аналогично вычислим
:
Окончательно запишем:
, а
.
Способ второй. Присвоение веса коэффициентам в соответствии со значением оптимальной весовой функции.
С учётом симметричности сигнального импульса (8) относительно оси ординат, рассмотрим временной интервал
разделённый на две равные части. Присвоим коэффициентам
и
квазиоптимальной ВФ
веса, соответствующие значениям оптимальной ВФ в точках
и
(на серединах установленных интервалов) как показано на рис. 4. Запишем соотношения для расчёта искомых коэффициентов:
откуда
, и
.
Возможна многоступенчатая аппроксимация оптимальной ВФ. На рис. 5 показана квазиоптимальная ВФ
состоящая из восьми ступеней. Интервал наблюдения
разделён на восемь равных частей длительностью
.
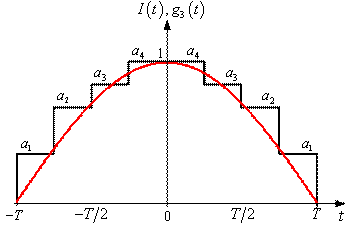
Рис. 5
Восьмиступенчатая аппроксимация оптимальной весовой функции
Коэффициенты
и
выберем равными
и
соответственно, где
– амплитудное значение сигнального импульса (8) (на рис. 5 ради простоты принято равным единице); коэффициент
выберем равным
; коэффициент
определим как значение середины интервала на оси ординат между значениями
и
, тогда
. При
, коэффициенты квазиоптимальной ВФ
имеют значения:
;
;
;
.
Увеличивая число ступеней у функции аппроксимирующей оптимальную ВФ, можно достичь пренебрежимо малых потерь в помехоустойчивости при равновесовой обработке ШПС-МЧМ, однако при этом объём вычислительных затрат при реализации квазиоптимальных алгоритмов приближается к объёму вычислительных затрат при реализации оптимального алгоритма.
Статистическое моделирование алгоритмов корреляционной обработки шумоподобных сигналов с минимальной частотной манипуляцией
Для оценки помехоустойчивости квазиоптимальных алгоритмов корреляционной обработки ШПС-МЧМ, основанных на замене оптимальных опорных сигналов (2) на квазиоптимальные ВФ, воспользуемся методом статистического моделирования. Будем полагать, что на вход коррелятора поступает аддитивная смесь сигнального импульса (8) с амплитудой
и белого гауссова шума. Выходная величина коррелятора, в зависимости от вида ВФ, является энергией (оптимальная ВФ), либо взаимной энергией входного и опорного импульсов. Для
-ой ВФ выходная величина коррелятора определится соотношением:
Переходя в (16) к дискретному времени
запишем выходную величину коррелятора для
-ого испытания (
– интервал дискретизации):
где
– целое,
–
-ая реализация шума. В качестве критерия помехоустойчивости используем отношение сигнал/шум на выходе коррелятора
, где
– математическое ожидание выходной величины коррелятора,
– среднеквадратическое отклонение величины
.
Проводя
испытаний, оценку отношения сигнал/шум на выходе коррелятора для
-ой ВФ представим в виде
где
– оценка величины
, а
– оценка дисперсии
. При ВФ вида (8) отношение сигнал/шум
является оценкой потенциально достижимого отношения сигнал/шум
. Проигрыш в помехоустойчивости квазиоптимальных алгоритмов корреляционной обработки ШПС-МЧМ
, выраженный в
, запишем в виде
Статистическое моделирование алгоритмов корреляционной обработки ШПС-МЧМ проведено в системе MathCAD 11 Enterprise Edition при числе испытаний
. Результаты моделирования сведены в таблицу 1.
Таблица 1
ВЕСОВАЯ
ФУНКЦИЯ
ПРИМЕЧАНИЕ
1
0
Оптимальная
0,888
– 1,029
0,967
– 0,211
,
0,978
– 0,195
,
0,993
– 0,063
,
,
,
Из таблицы 1 видно, что минимальный проигрыш в помехоустойчивости обеспечивает ВФ вида
, с восьмью ступенями аппроксимации оптимальной ВФ. Наиболее перспективной является функция
, обеспечивающая приемлемый проигрыш в помехоустойчивости (около
) и относительно простую реализацию квазиоптимальных алгоритмов корреляционной обработки ШПС-МЧМ.
Выводы
Разработаны квазиоптимальные алгоритмы равновесовой корреляционной обработки ШПС-МЧМ. Предложено два способа аппроксимации оптимальной ВФ четырьмя аппроксимирующими ступенями, знаковая аппроксимация, а также способ многоуровневой аппроксимации. Проведён расчет коэффициентов кусочно-заданных квазиоптимальных весовых функций.
Проведено статистическое моделирование и оценены проигрыши в помехоустойчивости разработанных квазиоптимальных алгоритмов равновесовой корреляционной обработки ШПС-МЧМ. При многоуровневой аппроксимации (восемь ступеней) оптимальной ВФ потери в помехоустойчивости не превышают
, однако наиболее перспективной является квазиоптимальная функция
с коэффициентами
и
, обеспечивающая приемлемый проигрыш в помехоустойчивости (менее
) и относительно простую реализацию квазиоптимальных алгоритмов корреляционной обработки ШПС-МЧМ. Алгоритм корреляционной обработки ШПС-МЧМ с использованием квазиоптимальной весовой функции
легко реализован на современной цифровой элементной базе и использован при разработке перспективной РНС для морской навигации.
Библиографический список
1. Кокорин В.И. Радионавигационные системы и устройства: Учеб. пособие / В.И. Кокорин. – Красноярск: ИПЦ КГТУ, 2006. – 175 с.
2. Алёшечкин А.М., Бондаренко В.Н., Бяков А.Г., Кокорин В.И., Кузьмин Е.В. Бортовая станция широкополосной системы морской радионавигации / Радиолокация, навигация и связь: сб. научн. тр. международной НТК. Том 3. Стр. 1932 – 1942. Воронеж, 2007.
3. Кузьмин Е.В., Бондаренко В.Н. Цифровой фазовый дискриминатор шумоподобного сигнала с минимальной частотной манипуляцией. Современные проблемы радиоэлектроники: сб. науч. тр. / Под ред. А.И. Громыко, А.В. Сарафанова. Стр. 83 – 86. Красноярск: ИПЦ КГТУ, 2005. – 732 с.
4. Варакин Л.Е. Системы связи с шумоподобными сигналами. – М.: Радио и связь, 1985. – 384 с.
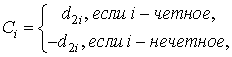
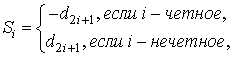
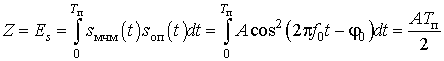 ,
,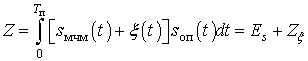 ,
,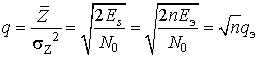 ,
,
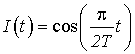 .
.
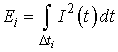 ,
,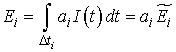 ,
,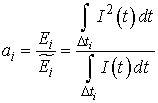 .
.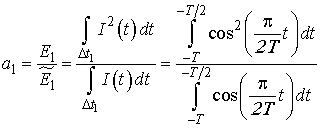 ,
,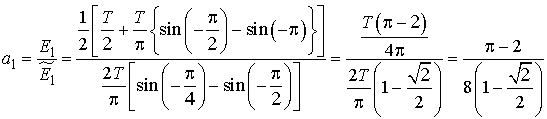 .
.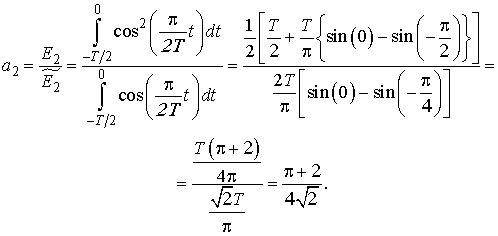
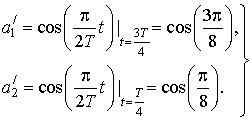 ,
,
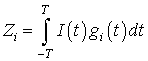 .
.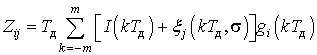 ,
,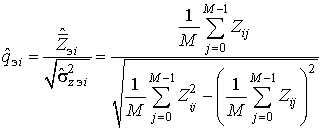 ,
,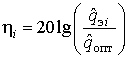 .
.