УДК 621.396.67
МНОГОПРОВОДНЫЕ КВАДРИФИЛЯРНЫЕ АНТЕННЫ
С. Е. Банков1,
А. Бычков2, А. Г. Давыдов2, А. А. Курушин3
1ИРЭ им. В.А. Котельникова РАН, 2МКБ Компас, 3МЭИ
(ТУ)
Получена 30 августа 2010 г.
Аннотация. Рассматриваются многопроводные
квадрифилярные антенны, образованные четырьмя спиральными излучателями, каждый
из которых представляет собой структуру, состоящую из нескольких проводников.
Исследованы следующие варианты многопроводных квадрифилярных антенн:
четвертьволновая с двумя и тремя проводниками и полуволновая с двумя и тремя
проводниками. Предложена феноменологическая теория таких антенн, позволяющая
качественно оценить их характеристики. Представлены результаты численного и
экспериментального исследования квадрифилярных антенн.
Ключевые слова: квадрифилярная антенна, спиральная антенна, многопроводная спиральная антенна.
1. Постановка задачи
Квадрифилярные спиральные антенны (КСА) хорошо известны в антенной технике (см., например, [1], [2]). Они используются в различных радиоэлектронных системах в качестве антенн круговой поляризации, которые имеют достаточно малые габариты и обеспечивают направленное одностороннее излучение.
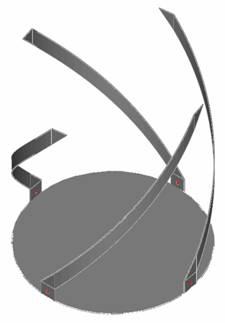
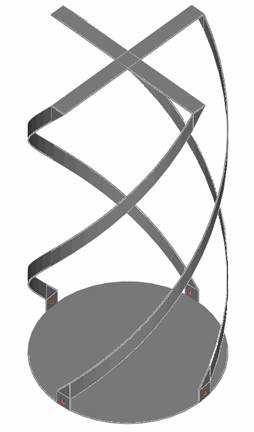
В данной работе рассматриваются малогабаритные КСА, функционирующие в резонансном режиме, который наблюдается, когда длина спиральных излучателей (СИ) близка к четверти или половине длины волны в свободном пространстве. На рис. 1 а,б показаны традиционные четвертьволновая (рис. 1 а) и полуволновая (рис. 1 б) КСА.
а б
Рис. 1. Четвертьволновая (а) и полуволновая (б) КСА
Каждый спиральный излучатель представляет собой один металлический проводник, изогнутый вдоль спиральной линии. Антенна имеет основание, на котором расположены элементы питания, возбуждающие СИ. Известна полуволновая КСА с одним элементом питания [3]. В данной работе рассматриваются КСА с четырьмя элементами питания. Напряжения на этих элементах формируются специальной схемой питания КСА. В идеальном случае для создания излучения круговой поляризации эти напряжения должны иметь одинаковые амплитуды и быть сдвинуты по фазе на 900 друг относительно друга. Функционирование схемы питания не является предметом нашей работы. Мы полагаем, что она выполняет свою функцию идеально. Также считаем, что четыре ее выхода развязаны друг с другом. Отметим, что четырехэлементное питание является оптимальным для КСА и не создает противоречия между требованием согласования антенны и требованием к поляризационным характеристикам ее излучения, которое характерно для одноэлементного питания.
Таким образом, СИ одними
концами соединяются с элементами питания. Другие их концы в зависимости от типа
антенны разомкнуты (четвертьволновая КСА) или замкнуты друг с другом перемычками
(полуволновая КСА). Разные электрические режимы на концах СИ необходимы для
создания условий резонанса на частоте ![]() , которая является центральной частотой
рабочего диапазона. Нетрудно сделать вывод о том, что четвертьволновая КСА
функционирует как резонатор на основе отрезка линии передачи (ЛП), который
закорочен на одном конце (роль короткозамыкателя играет основание КСА) и
разомкнут на другом. Аналогично полуволновая КСА функционирует как отрезок ЛП,
закороченный с двух сторон. При этом настройка антенны на рабочую частоту
достигается выбором длины СИ, которая в одном случае равна
, которая является центральной частотой
рабочего диапазона. Нетрудно сделать вывод о том, что четвертьволновая КСА
функционирует как резонатор на основе отрезка линии передачи (ЛП), который
закорочен на одном конце (роль короткозамыкателя играет основание КСА) и
разомкнут на другом. Аналогично полуволновая КСА функционирует как отрезок ЛП,
закороченный с двух сторон. При этом настройка антенны на рабочую частоту
достигается выбором длины СИ, которая в одном случае равна ![]() , а в другом
, а в другом ![]() , где
, где ![]() - длина волны в свободном
пространстве на частоте
- длина волны в свободном
пространстве на частоте ![]() .
.
Простейшие КСА, показанные
на рис. 1 а,б, имеют свободные параметры, к которым относятся угол намотки
спирали ![]() и ее диаметр
и ее диаметр ![]() . Меняя их, можно регулировать
характеристики излучения антенны: ее диаграмму направленности (ДН) и коэффициент
эллиптичности (КЭ). Среди свободных параметров также можно отметить диаметр
проводника
. Меняя их, можно регулировать
характеристики излучения антенны: ее диаграмму направленности (ДН) и коэффициент
эллиптичности (КЭ). Среди свободных параметров также можно отметить диаметр
проводника ![]() , если он имеет круглую
форму поперечного сечения, или ширину
, если он имеет круглую
форму поперечного сечения, или ширину ![]() , когда в качестве проводника используется
металлическая лента. Однако размеры и форма сечения проводника весьма слабо
влияют на характеристики КСА и, в первом приближении, их изменение может не
приниматься во внимание. Таким образом, мы можем сделать вывод о том, что в
простейших схемах КСА отсутствуют параметры, управляющие величиной входного
сопротивления антенны. В то же время, этот параметр существенно влияет на
функционирование КСА и во многом определяет ее коэффициент усиления (КУ) и
коэффициент полезного действия (КПД).
, когда в качестве проводника используется
металлическая лента. Однако размеры и форма сечения проводника весьма слабо
влияют на характеристики КСА и, в первом приближении, их изменение может не
приниматься во внимание. Таким образом, мы можем сделать вывод о том, что в
простейших схемах КСА отсутствуют параметры, управляющие величиной входного
сопротивления антенны. В то же время, этот параметр существенно влияет на
функционирование КСА и во многом определяет ее коэффициент усиления (КУ) и
коэффициент полезного действия (КПД).
Поэтому актуальной задачей является разработка и исследование новых вариантов КСА, позволяющих осуществлять независимую настройку входного сопротивления антенны и, следовательно, ее согласование со схемой питания. Поставленная задача может быть решена, если вместо СИ из одиночного проводника используется СИ, образованный несколькими проводниками. Исследованию КСА с многопроводными СИ посвящена данная работа. Для определенности будем далее рассматривать КСА, образованные ленточными проводниками, которые могут быть выполнены в рамках технологии печатных схем и обеспечивают высокую технологичность всей конструкции антенны.
4. Феноменологическая модель четвертьволновой КСА с многопроводными СИ
Под феноменологической моделью будем понимать модель, качественно верно передающую основные явления в моделируемом объекте, но непригодную для количественного его анализа из-за присутствия в модели параметров, которые остаются неопределенными в рамках принятого способа описания объекта.
Конструкция четвертьволновой КСА с многопроводными СИ показана на рис. 2.
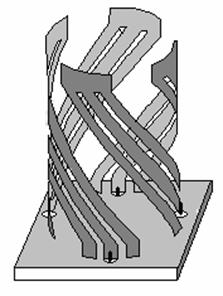
Рис. 2. Четвертьволновая КСА с трехпроводными СИ
На рис. 2 изображена
антенна с трехпроводными СИ. Структура СИ с произвольным числом проводников
поясняется на рис. 3. В общем случае число проводников равно ![]() . Их ширины равны
. Их ширины равны ![]() ,
, ![]() . Расстояния между проводниками
равны
. Расстояния между проводниками
равны ![]() ,
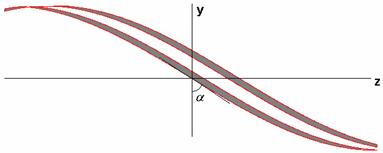
, ![]() . На рис. 4 схематично показаны два вида СИ.
Вид на рис. 4 а поясняет смысл угла намотки спирали
. На рис. 4 схематично показаны два вида СИ.
Вид на рис. 4 а поясняет смысл угла намотки спирали
![]() , а вид на рис.
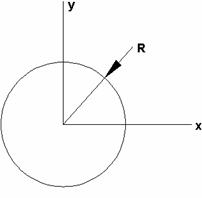
4 б показывает окружность радиуса
, а вид на рис.
4 б показывает окружность радиуса ![]() , вдоль которой намотана спираль.
, вдоль которой намотана спираль.
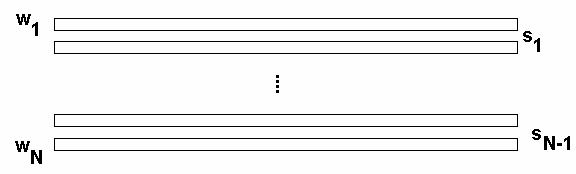
Рис. 3. Многопроводный СИ
а б
Рис. 4. Многопроводный СИ и его параметры
Поясним основной принцип функционирования четвертьволновой КСА. Он аналогичен
принципу, по которому в вибраторе Пистолькорса [4] происходит увеличение
входного сопротивления по сравнению с полуволновым вибратором, выполненным из
одного проводника. Вибратор Пистолькорса можно рассматривать также как
излучатель, образованный многопроводной линией передачи. В таком случае КСА,
показанная на рис. 2, может рассматриваться как антенна, образованная четырьмя
вибраторами Пистолькорса. Важно только, что в традиционном варианте вибратор
имеет размер в половину длины волны, а в нашем случае используется его половина
длиною ![]() (
(![]() - длина волны в свободном пространстве).
Элементарная теория такого излучателя показывает, что его входное сопротивление
должно возрасти по сравнению с обычным вибратором в четыре раза. Исходя из этого
факта, можно рассчитывать, что и в КСА мы можем добиться увеличения входного
сопротивления.
- длина волны в свободном пространстве).
Элементарная теория такого излучателя показывает, что его входное сопротивление
должно возрасти по сравнению с обычным вибратором в четыре раза. Исходя из этого
факта, можно рассчитывать, что и в КСА мы можем добиться увеличения входного
сопротивления.
Важным для обоснования феноменологическая модель моментом является представление
КСА как многопроводной линии передачи. В направляющей структуре содержащей ![]() металлических
проводника, могут распространяться
металлических
проводника, могут распространяться
![]() основные
волны. Однако нас интересуют не все волны, а лишь те, которые могут возбудиться
схемой питания, которая в идеальном случае создает на входах СИ одинаковые по
амплитуде напряжения сдвинутые друг относительно друга на 900. Такое
возбуждение эквивалентно возбуждению двумя источниками с напряжениями
основные
волны. Однако нас интересуют не все волны, а лишь те, которые могут возбудиться
схемой питания, которая в идеальном случае создает на входах СИ одинаковые по
амплитуде напряжения сдвинутые друг относительно друга на 900. Такое
возбуждение эквивалентно возбуждению двумя источниками с напряжениями
![]() , которые
подключаются к излучателям, сдвинутым друг относительно друга на 1800
(см. рис. 5).
, которые
подключаются к излучателям, сдвинутым друг относительно друга на 1800
(см. рис. 5).
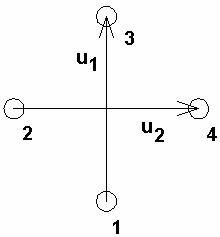
Рис. 5. Возбуждение излучателей КСА
При этом напряжения ![]() сдвинуты по фазе друг
относительно друга на 900 и имеют одинаковые амплитуды. Можно строго
показать [5], что указанные выше источники напряжения возбуждают
электромагнитные поля ортогональные друг другу. В частности, ортогональность
этих полей означает, что источник
сдвинуты по фазе друг
относительно друга на 900 и имеют одинаковые амплитуды. Можно строго
показать [5], что указанные выше источники напряжения возбуждают
электромагнитные поля ортогональные друг другу. В частности, ортогональность
этих полей означает, что источник ![]() наводит токи только на СИ 1 и 3
(см. рис. 5) и не наводит на СИ 2 и 3. Аналогичное утверждение справедливо для
источника
наводит токи только на СИ 1 и 3
(см. рис. 5) и не наводит на СИ 2 и 3. Аналогичное утверждение справедливо для
источника ![]() , возбуждающего СИ 2 и 3.
Описанная выше ситуация обусловлена особым видом винтовой симметрии, характерным
для спиральных структур. Благодаря данному свойству КСА, мы можем рассматривать
волны в парах СИ независимо друг от друга. При этом полное поле в антенне будет
линейной комбинацией полей двух пар СИ.
, возбуждающего СИ 2 и 3.
Описанная выше ситуация обусловлена особым видом винтовой симметрии, характерным
для спиральных структур. Благодаря данному свойству КСА, мы можем рассматривать
волны в парах СИ независимо друг от друга. При этом полное поле в антенне будет
линейной комбинацией полей двух пар СИ.
На основании изложенных выше положений мы можем рассмотреть показанную на рис. 6 схему, являющуюся моделью четвертьволновой КСА.
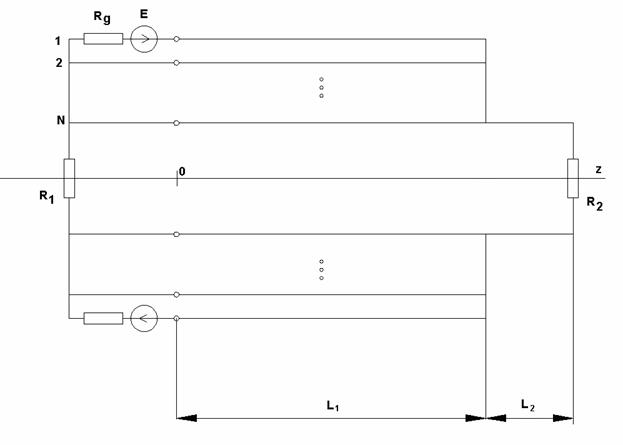
Рис. 6. Эквивалентная схема четвертьволновой КСА с многопроводными СИ
Проводники в верхней и
нижней части схемы соответствуют проводникам двух СИ. В два из них включены
источники напряжения ![]() с внутренним
сопротивлением
с внутренним
сопротивлением
![]() , которые
моделируют элементы питания КСА. Источники напряжения в верхней и нижней
половине схемы сдвинуты по фазе на 1800. Данное обстоятельство вместе
с геометрической симметрией схемы относительно оси 0z позволяет
рассматривать одну половину схемы, которая получается из исходной сечением ее
идеально проводящей стенкой, проходящей через ось 0z [6]. При этом сопротивления
, которые
моделируют элементы питания КСА. Источники напряжения в верхней и нижней
половине схемы сдвинуты по фазе на 1800. Данное обстоятельство вместе
с геометрической симметрией схемы относительно оси 0z позволяет
рассматривать одну половину схемы, которая получается из исходной сечением ее
идеально проводящей стенкой, проходящей через ось 0z [6]. При этом сопротивления
![]() заменяются
сопротивлениями
заменяются
сопротивлениями
![]() .
.
Резисторы
![]() описывают
потери энергии, обусловленные излучением из КСА. Отметим, что собственные волны
любой линии передачи распространяются вдоль нее без излучения. Излучение
происходит в местах нарушения регулярности направляющей структуры. В нашем
случае имеется два таких места: основание КСА и обрыв СИ. Именно в этих местах
включены сопротивления
описывают
потери энергии, обусловленные излучением из КСА. Отметим, что собственные волны
любой линии передачи распространяются вдоль нее без излучения. Излучение
происходит в местах нарушения регулярности направляющей структуры. В нашем
случае имеется два таких места: основание КСА и обрыв СИ. Именно в этих местах
включены сопротивления
![]() .
.
Пусть многопроводная линия имеет длину ![]() , оконечная часть СИ выполнена в виде
однопроводной линии передачи длиной
, оконечная часть СИ выполнена в виде
однопроводной линии передачи длиной ![]() . Общая длина СИ таким образом равна
. Общая длина СИ таким образом равна ![]() +
+![]() .
.
Напряжения и токи в многопроводной линии передачи могут быть описаны в виде
суммы собственных волн. Если проводники расположены в однородной среде, в нашем
случае воздухе, то основными волнами являются Т – волны, имеющие одинаковые
постоянные распространения, совпадающие с волновым числом свободного
пространства
![]() . Их число
равно
. Их число
равно ![]() . При этом линия передачи содержит
. При этом линия передачи содержит ![]() проводник, если в их число
включить общий проводник (см. рис. 7).
проводник, если в их число
включить общий проводник (см. рис. 7).
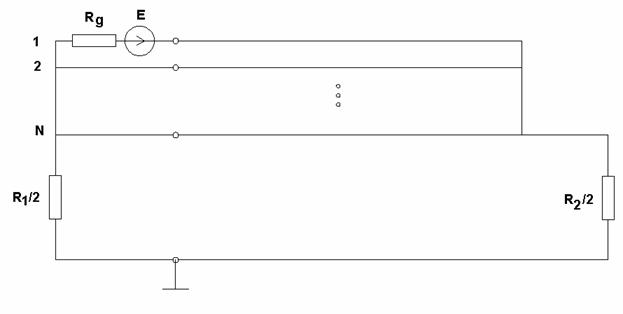
Рис. 7. Эквивалентная схема КСА с общим проводником
Будем понимать под напряжением ![]() в проводнике с номером
в проводнике с номером ![]() ,
, ![]() разность потенциалов между данным
проводником и общим проводником. Без потери общности можно считать потенциал
общего проводника равным нулю. В качестве положительного направления тока в
проводнике выберем положительное направление оси 0z.
Тогда собственную волну номера
разность потенциалов между данным
проводником и общим проводником. Без потери общности можно считать потенциал
общего проводника равным нулю. В качестве положительного направления тока в
проводнике выберем положительное направление оси 0z.
Тогда собственную волну номера ![]() ,
, ![]() можно описать с помощью
следующего вектора
можно описать с помощью
следующего вектора ![]() :
:
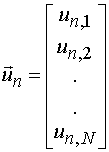 , (1)
, (1)
где ![]() - напряжения волны с
номером
- напряжения волны с
номером ![]() в проводнике с номером
в проводнике с номером ![]() .
.
Токи собственной волны также можно объединить в вектор ![]() :
:
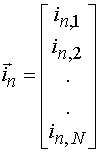 . (2)
. (2)
Вектора
![]() и
и ![]() связаны
характеристическим сопротивлением
связаны
характеристическим сопротивлением
![]() или
проводимостью
или
проводимостью
![]() (
(![]() ):
):
![]() =
=![]()
![]() . (3)
. (3)
Верхний знак соответствует волне, распространяющейся в положительном, а нижний - в отрицательном направлениях оси 0z. Напряжение и ток в проводниках линии передачи является суммой собственных волн, распространяющихся как в положительном, так и в отрицательном направлениях:
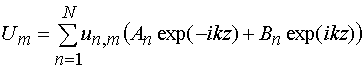 , (4)
, (4)
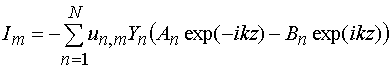 ,
,
где ![]() - амплитуды прямых и
встречных волн соответственно. Эти амплитуды на данном этапе неизвестны. Они
будут найдены из граничных условий, которые необходимо выполнить на концах
регулярной линии передачи при
- амплитуды прямых и
встречных волн соответственно. Эти амплитуды на данном этапе неизвестны. Они
будут найдены из граничных условий, которые необходимо выполнить на концах
регулярной линии передачи при ![]() . Отметим, что ток в
нулевом проводнике
. Отметим, что ток в
нулевом проводнике ![]() равен сумме токов в
проводниках с номерами
равен сумме токов в
проводниках с номерами ![]() с обратным знаком:
с обратным знаком:
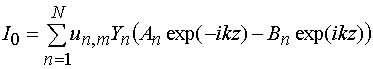 . (5)
. (5)
Граничные условия при ![]() можно получить, выполняя
закон Ома:
можно получить, выполняя
закон Ома:
![]() , (6)
, (6)
где 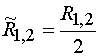 ,
, ![]() - э.д.с. источника напряжения,
- э.д.с. источника напряжения, ![]() - символ Кронекера,
- символ Кронекера, ![]() - номер проводника, в
который включен источник напряжения. В развернутой форме граничное условие при
- номер проводника, в
который включен источник напряжения. В развернутой форме граничное условие при ![]() имеет следующий вид:
имеет следующий вид:
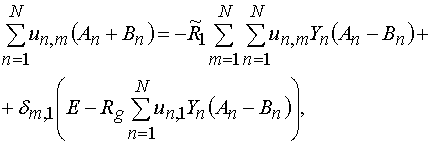 (7)
(7)
![]() .
.
Для вывода граничных условий при ![]() мы можем эквивалентно
представить отрезок однопроводной линии передачи длиной
мы можем эквивалентно
представить отрезок однопроводной линии передачи длиной ![]() , нагруженный на сопротивление
, нагруженный на сопротивление
![]() , в виде
сопротивления
, в виде
сопротивления
![]() , на которое
нагружена многопроводная линия в сечении
, на которое
нагружена многопроводная линия в сечении ![]() . Для сопротивления
. Для сопротивления
![]() можно получить
следующее выражение, если воспользоваться известным соотношением [4],
описывающим трансформацию импедансов вдоль линии передачи:
можно получить
следующее выражение, если воспользоваться известным соотношением [4],
описывающим трансформацию импедансов вдоль линии передачи:
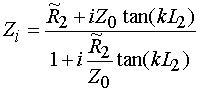 , (8)
, (8)
где ![]() - характеристический
импеданс однопроводной линии.
- характеристический
импеданс однопроводной линии.
Используя формулу (8),
получаем граничное условие при ![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
В развернутой форме условия принимают следующий вид:
![]() , (9)
, (9)
![]() .
.
Уравнения (7), (9) можно рассматривать в качестве системы линейных
алгебраических уравнений относительно неизвестных амплитуд волн. Порядок системы ![]() .
.
Напряжения и характеристические сопротивления собственных волн должны быть
получены из решения специально сформулированной задачи [7]. Для ряда частных
случаев, которые представляют наибольший практический интерес, вектора ![]() могут быть получены без сложных расчетов,
исходя из симметрии структуры и свойства ортогональности собственных волн. К
таким случаям относятся линии передачи с двумя проводниками.
могут быть получены без сложных расчетов,
исходя из симметрии структуры и свойства ортогональности собственных волн. К
таким случаям относятся линии передачи с двумя проводниками.
Под ортогональностью собственных волн понимается следующее соотношение:
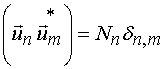 , (10)
, (10)
где ![]() - норма собственной
волны, а звездочка означает операцию комплексного сопряжения. Произведение в скобках, стоящее в
формуле (10), является скалярным произведением двух векторов.
Для простоты будем считать, что
нормы всех волн равны единице.
- норма собственной
волны, а звездочка означает операцию комплексного сопряжения. Произведение в скобках, стоящее в
формуле (10), является скалярным произведением двух векторов.
Для простоты будем считать, что
нормы всех волн равны единице.
С учетом соотношения (10) можно получить для линии передачи с двумя одинаковыми проводниками следующее выражение для собственных волн [7]:
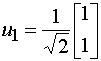 , (11)
, (11)
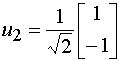 ,
,
Собственные волны симметричной двухпроводной линии передачи принято называть четной и нечетной.
Можно также получить выражения для собственных волн симметричной линии передачи с тремя одинаковыми проводниками. Для такой структуры справедливы следующие соотношения:
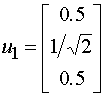 ,
,
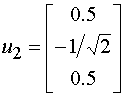 , (12)
, (12)
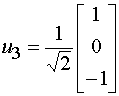 .
.
Для определения
характеристических сопротивлений собственных волн можно воспользоваться
следующими качественными соображениями. Поясним их на примере линии передачи с
двумя проводниками. Ее поперечное сечение показано на рис. 8. Ленточные
металлические проводники размещены на поверхности цилиндра диаметра ![]() . Они имеют ширину
. Они имеют ширину ![]() , а расстояние между ними
равно
, а расстояние между ними
равно ![]() . Как правило, между параметрами линии
передачи выполняются следующие соотношения:
. Как правило, между параметрами линии
передачи выполняются следующие соотношения:
![]() . (13)
. (13)
Благодаря неравенству (13) влиянием кривизны цилиндрической поверхности можно
пренебречь и считать ее локально плоской. Тогда в силу симметрии структуры
относительно горизонтальной плоскости, проходящей через ось цилиндра, в ней
можно расположить идеально проводящую стенку и рассматривать новую структуру,
которая представляет собой две металлические полоски, расположенные на
расстоянии ![]() над поверхностью
металлического проводника.
над поверхностью
металлического проводника.

Рис. 8. Поперечное сечение многопроводной линии передачи
Волны такой двухпроводной микрополосковой линии с воздушной подложкой хорошо изучены [8]. Одна из них – четная волна – соответствует размещению между полосковыми проводниками магнитной стенки, а другая – нечетная волна – электрической. Для характеристических сопротивлений четной и нечетной волн получены приближенные формулы [7]. Их точность адекватна уровню строгости феноменологической модели.
Рассмотрим далее численные примеры использования феноменологической модели. В
качестве первого шага изучим частотные зависимости действительной
![]() и мнимой
и мнимой ![]() частей входного сопротивления КСА с
одпроводными СИ. Антенна имеет следующие параметры:
частей входного сопротивления КСА с
одпроводными СИ. Антенна имеет следующие параметры: ![]() =13,
=13, ![]() =2,
=2, ![]() =50. Сопротивления
=50. Сопротивления
![]() были взяты равными 5 и 7000 Ом
соответственно. Выбор этих параметров будет обсуждаться ниже. Все размеры здесь
и далее приводятся в миллиметрах.
были взяты равными 5 и 7000 Ом
соответственно. Выбор этих параметров будет обсуждаться ниже. Все размеры здесь
и далее приводятся в миллиметрах.
На рис. 9 кривые 1 и 2 соответствуют частотным зависимостям
![]() и
и ![]() . Видно, что кривые имеют
три характерные точки. Две из них соответствуют параллельным резонансам при
. Видно, что кривые имеют
три характерные точки. Две из них соответствуют параллельным резонансам при ![]() =0
и
=0
и ![]() =3 ГГц, а
одна последовательному резонансу при
=3 ГГц, а
одна последовательному резонансу при ![]() =1.5
ГГц. На частотах параллельных резонансов активная часть входного сопротивления
антенны сильно растет, а на последовательном резонансе, наоборот становится
весьма малой величиной. В рассматриваемом примере она составляет примерно 10 Ом.
Видно, что спектр собственных частот КСА эквидистантный. Он соответствует
спектру четвертьволнового резонатора. Рабочим колебанием является
последовательный резонанс с частотой
=1.5
ГГц. На частотах параллельных резонансов активная часть входного сопротивления
антенны сильно растет, а на последовательном резонансе, наоборот становится
весьма малой величиной. В рассматриваемом примере она составляет примерно 10 Ом.
Видно, что спектр собственных частот КСА эквидистантный. Он соответствует
спектру четвертьволнового резонатора. Рабочим колебанием является
последовательный резонанс с частотой ![]() .
.
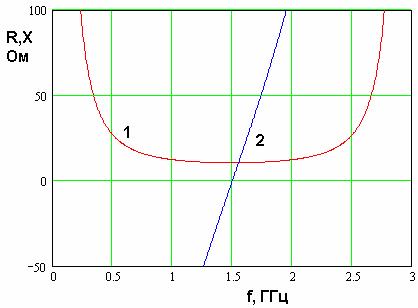
Рис. 9. Частотная зависимость входного сопротивления четвертьволновой КСА с однопроводными СИ
Выбор параметров ![]() в рамках феноменологической модели сделать невозможно.
Они описывают потери на излучение в свободное пространство и определяют значение
активной части входного сопротивления на резонансной частоте. Для определения
сопротивлений
в рамках феноменологической модели сделать невозможно.
Они описывают потери на излучение в свободное пространство и определяют значение
активной части входного сопротивления на резонансной частоте. Для определения
сопротивлений
![]() нужно задаться указанным значением
входного сопротивления, которое может быть найдено из более точной модели КСА,
например, полученной путем численного решения электродинамической задачи.
нужно задаться указанным значением
входного сопротивления, которое может быть найдено из более точной модели КСА,
например, полученной путем численного решения электродинамической задачи.
Таким образом, мы можем сделать вывод, что активная часть входного сопротивления
КСА имеет недостаточное значение, равное 10 Ом. Рассмотрим теперь КСА со СИ,
выполненными из двух проводников. Расстояние между ними ![]() равно 2, также пусть
равно 2, также пусть ![]() =0. На рис. 10 показаны
частотные зависимости сопротивлений
=0. На рис. 10 показаны
частотные зависимости сопротивлений
![]() и
и ![]() , которым соответствуют
кривые 1 и 2.
, которым соответствуют
кривые 1 и 2.
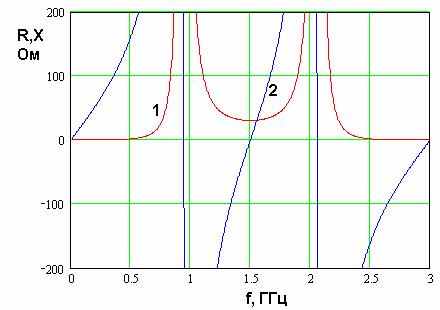
Рис. 10. Частотная зависимость входного сопротивления четвертьволновой КСА с двухпроводными СИ
Из рис. 10 видно, что КСА со СИ из двух проводников имеет неэквидистантный
спектр собственных частот. Частоты параллельных резонансов сдвинулись к частоте ![]() . Благодаря этому сопротивление
. Благодаря этому сопротивление
![]() на этой
частоте возросло и равно теперь примерно 30. Положение частот параллельных
резонансов и, соответственно, величина действительной части входного
сопротивления на частоте
на этой
частоте возросло и равно теперь примерно 30. Положение частот параллельных
резонансов и, соответственно, величина действительной части входного
сопротивления на частоте ![]() зависят от параметров
зависят от параметров ![]() и
и ![]() .
.
На рис. 11 показана зависимость сопротивления
![]() на частоте
последовательного резонанса
на частоте
последовательного резонанса ![]() от ширины проводника
от ширины проводника ![]() . Кривые 1 – 5
соответствуют
. Кривые 1 – 5
соответствуют
![]() =2,1.5,1,0.5,0.1.
Видно, что выбором значений
=2,1.5,1,0.5,0.1.
Видно, что выбором значений ![]() и
и ![]() мы можем добиться равенства
сопротивления
мы можем добиться равенства
сопротивления
![]() стандартному
значению 50 Ом.
стандартному
значению 50 Ом.
Использование трехпроводной линии позволяет осуществлять преобразование входного
сопротивления антенны в еще больших пределах, чем в рассмотренном выше случае.
Сопротивления
![]() в
рассматриваемом численном примере равны 1 и 40000 Ом, что соответствует входному
сопротивлению КСА на частоте
в
рассматриваемом численном примере равны 1 и 40000 Ом, что соответствует входному
сопротивлению КСА на частоте ![]() , равному 2 Ом.
, равному 2 Ом.
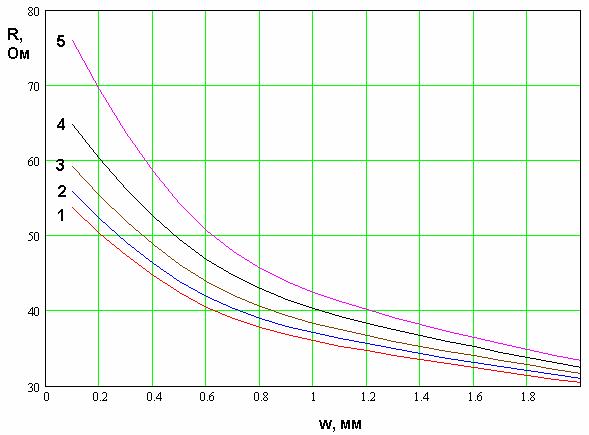
Рис. 11. Зависимость действительной части входного импеданса четвертьволновой КСА с двухпроводными СИ от ширины проводника при разных расстояниях между проводниками
Частотные зависимости импедансов ![]() и
и ![]() в данном случае
качественно мало отличаются от представленных на рис. 10. Частоты параллельных
резонансов приближены к частоте
в данном случае
качественно мало отличаются от представленных на рис. 10. Частоты параллельных
резонансов приближены к частоте ![]() в еще большей степени, чем в КСА с
двухпроводными СИ. За счет этого степень преобразования входного сопротивления
увеличивается. В этом можно убедиться, анализируя рис. 12, на котором показана
зависимость параметра
в еще большей степени, чем в КСА с
двухпроводными СИ. За счет этого степень преобразования входного сопротивления
увеличивается. В этом можно убедиться, анализируя рис. 12, на котором показана
зависимость параметра ![]() от ширины проводника
от ширины проводника ![]() при разных расстояниях
между проводниками. Кривые 1 – 5 соответствуют
при разных расстояниях
между проводниками. Кривые 1 – 5 соответствуют
![]() =1.5, 2, 2.5,
3, 3.5.
=1.5, 2, 2.5,
3, 3.5.
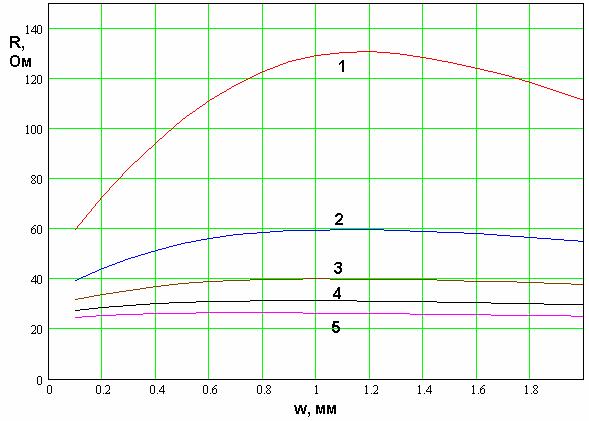
Рис. 12. Зависимость действительной части входного импеданса четвертьволновой КСА с трехпроводными СИ от ширины проводников при разных расстояниях между ними
Функционирование КСА с двух- и трехпроводными СИ отличается также шириной полосы
согласования антенны. На рис. 13 показаны частотные зависимости модуля
коэффициента отражения от входа КСА. Кривая 1 соответствует двухпроводному СИ, а
кривая 2 трехпроводному. При этом параметры ![]() были одинаковыми для
обоих типов СИ. Они создавали входное сопротивление исходной однопроводной КСА,
равное 10 Ом. Таким образом, сравниваемые антенны находятся в одинаковых
условиях. Тем не менее, из рис. 13 видно, что полоса согласования КСА с
трехпроводными СИ шире, чем при использовании СИ из двух проводников.
были одинаковыми для
обоих типов СИ. Они создавали входное сопротивление исходной однопроводной КСА,
равное 10 Ом. Таким образом, сравниваемые антенны находятся в одинаковых
условиях. Тем не менее, из рис. 13 видно, что полоса согласования КСА с
трехпроводными СИ шире, чем при использовании СИ из двух проводников.
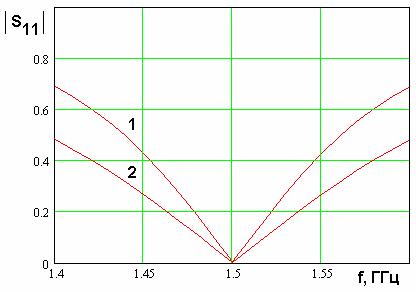
Рис. 13. Частотная зависимость модуля коэффициента отражения КСА с двух- и трехпроводными СИ
5. Феноменологическая модель полуволновой КСА с многопроводными СИ
Полуволновая КСА с двухпроводными СИ показана на рис. 14. В общем случае число
проводников, формирующих СИ на участке, примыкающем к точке соединения СИ со
схемой питания (![]() ) может равняться
) может равняться ![]() . Длина многопроводной
линии передачи равна
. Длина многопроводной
линии передачи равна ![]() . На участке
. На участке ![]() СИ имеет один проводник. Его длина равна
СИ имеет один проводник. Его длина равна ![]() .
.
Принципы работы полуволновой и четвертьволновой КСА отличаются друг от друга. В
полуволновой КСА используется идея смещения точки возбуждения СИ. В КСА с
однопроводными СИ (рис. 1 б) точка возбуждения располагается в начале СИ.
Основание антенны играет роль короткозамыкателя, который имеет сравнительно
небольшое активное сопротивление. Противоположные концы СИ замкнуты друг на
друга перемычками, которые также можно рассматривать в качестве нагрузок с малым
сопротивлением. Поскольку они расположены на расстоянии, близком к ![]() от точки возбуждения, то их
входное сопротивление, пересчитанное к этой точке, мало. Величину активной части
входного сопротивления можно регулировать только изменением диаметра КСА, от
которого зависит излучательная способность короткозамыкающих структур.
от точки возбуждения, то их
входное сопротивление, пересчитанное к этой точке, мало. Величину активной части
входного сопротивления можно регулировать только изменением диаметра КСА, от
которого зависит излучательная способность короткозамыкающих структур.
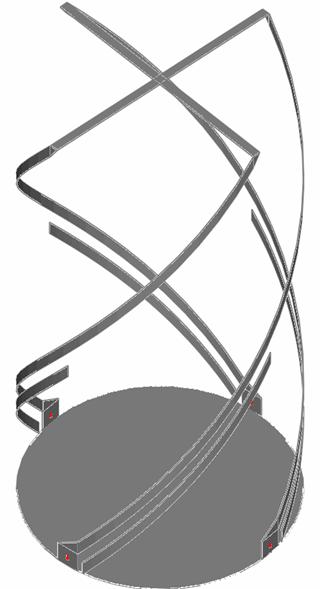
Рис. 14. Полуволновая КСА с двухпроводными СИ
Многопроводная линия передачи необходима для смещения точки возбуждения СИ на
расстояние
![]() . Ток, текущий
вдоль СИ распределен аналогично току в полуволновом резонаторе. Он имеет
максимумы на краях и равен нулю в центре СИ. Поэтому, смещая точку возбуждения,
мы получаем возможность в широких пределах менять входное сопротивление КСА,
равное отношению напряжения источника к току.
. Ток, текущий
вдоль СИ распределен аналогично току в полуволновом резонаторе. Он имеет
максимумы на краях и равен нулю в центре СИ. Поэтому, смещая точку возбуждения,
мы получаем возможность в широких пределах менять входное сопротивление КСА,
равное отношению напряжения источника к току.
В рамках феноменологической модели будем рассматривать эквивалентную схему КСА, показанную на рис. 15. Она может быть получена в рамках допущений, аналогичных принятым при анализе эквивалентной схемы четвертьволновой КСА (см. рис. 7).
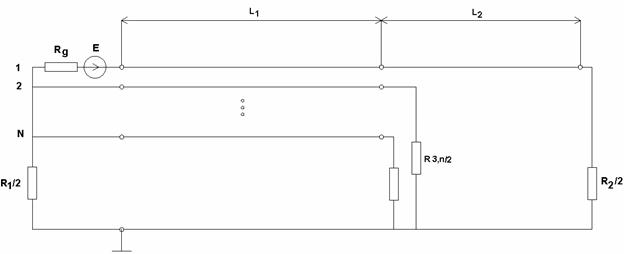
Рис. 15. Эквивалентная схема полуволновой КСА с многопроводными СИ
Сопротивления
![]() так же, как и
раньше, вводятся для описания излучения электромагнитной энергии с концов СИ.
Сопротивления
так же, как и
раньше, вводятся для описания излучения электромагнитной энергии с концов СИ.
Сопротивления
![]() ,
, ![]() описывают излучение с
концов многопроводной линии. Если в случае четвертьволновой КСА
сопротивление
описывают излучение с
концов многопроводной линии. Если в случае четвертьволновой КСА
сопротивление
![]() было малой
величиной, а
было малой
величиной, а ![]() большой, то сейчас оба
сопротивления малы, так как они описывают свойства короткозамыкающих перемычек
(в случае
большой, то сейчас оба
сопротивления малы, так как они описывают свойства короткозамыкающих перемычек
(в случае ![]() в роли такой перемычки выступает основание
антенны). Параметры
в роли такой перемычки выступает основание
антенны). Параметры ![]() , наоборот, являются
большими величинами, так как они соответствуют нагрузкам, близким к холостому
ходу.
, наоборот, являются
большими величинами, так как они соответствуют нагрузкам, близким к холостому
ходу.
Анализ КСА проводим аналогично рассмотренному выше случаю, используя собственные
волны многопроводной линии передачи. На участке ![]() , который назовем областью 1, напряжения и
токи в проводниках описываются соотношениями (4). На участке
, который назовем областью 1, напряжения и
токи в проводниках описываются соотношениями (4). На участке ![]() мы имеем однопроводную
линию передачи, напряжение и ток в которой записываются аналогичным образом:
мы имеем однопроводную
линию передачи, напряжение и ток в которой записываются аналогичным образом:
![]() , (14)
, (14)
![]() ,
,
где ![]() - амплитуды волн в линии
передачи,
- амплитуды волн в линии
передачи, ![]() - ее характеристическая
проводимость.
- ее характеристическая
проводимость.
Граничные условия для напряжений и токов при ![]() для полуволновой КСА не
отличаются от граничных условий (7). Для вывода условий в сечении
для полуволновой КСА не
отличаются от граничных условий (7). Для вывода условий в сечении ![]() удобно воспользоваться формулой для
входного сопротивления нагруженного отрезка линии передачи
удобно воспользоваться формулой для
входного сопротивления нагруженного отрезка линии передачи ![]() (8) и заменить отрезок
однопроводной линии передачи сопротивлением, включенным в сечении
(8) и заменить отрезок
однопроводной линии передачи сопротивлением, включенным в сечении ![]() между выходом проводника с
между выходом проводника с ![]() и общим проводником.
и общим проводником.
После замены отрезка линии передачи сопротивлением
![]() мы можем
записать граничные условия аналогичные условиям (9):
мы можем
записать граничные условия аналогичные условиям (9):
![]() , (15)
, (15)
![]() ,
,
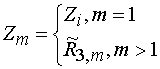 .
.
Подставляя в соотношение (15) выражения для токов и напряжений (4), получаем систему линейных алгебраических уравнений для определения амплитуд собственных волн:
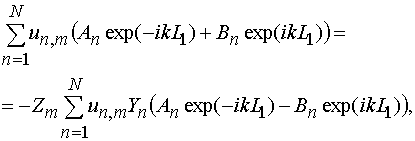 (16)
(16)
Систему (16) необходимо решать совместно с системой (7).
Рассмотрим далее результаты численного исследования полуволновой КСА с помощью феноменологической модели. На рис. 16 представлены частотные зависимости действительной и мнимой частей входного сопротивления КСА с однопроводными СИ. Им соответствуют кривые 1 и 2.
Графики построены для ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Видно, что КСА имеет два параллельных
резонанса на частотах 0.75 и 2.25 ГГц и последовательный резонанс на частоте 1.5
ГГц. Действительная часть входного импеданса на частоте 1.5 ГГц равна 5 Ом.
Низкое значение сопротивления
. Видно, что КСА имеет два параллельных
резонанса на частотах 0.75 и 2.25 ГГц и последовательный резонанс на частоте 1.5
ГГц. Действительная часть входного импеданса на частоте 1.5 ГГц равна 5 Ом.
Низкое значение сопротивления
![]() приводит к
недопустимо большому коэффициенту отражения от входа антенны, возбуждаемой
линией передачи с характеристическим импедансом в 50 Ом.
приводит к
недопустимо большому коэффициенту отражения от входа антенны, возбуждаемой
линией передачи с характеристическим импедансом в 50 Ом.
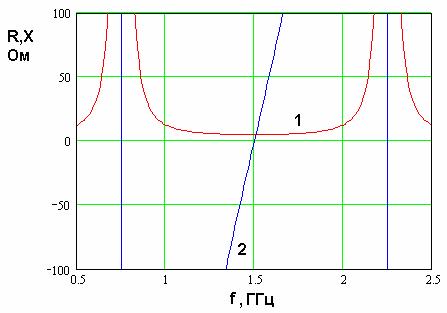
Рис. 16. Частотная зависимость входного сопротивления полуволновой КСА с однопроводными СИ
Качественно оценить влияние второго проводника СИ длиной ![]() можно, анализируя рис. 17, на
котором представлены частотные зависимости входных сопротивлений КСА
можно, анализируя рис. 17, на
котором представлены частотные зависимости входных сопротивлений КСА ![]() и
и
![]() . Кривые 1 и 2
соответствуют действительной и мнимой частям импеданса. Они получены при
. Кривые 1 и 2
соответствуют действительной и мнимой частям импеданса. Они получены при ![]() и
и
![]() =45. Из рис. 17
видно, что использование двухпроводного СИ приводит к появлению дополнительного
параллельного резонанса в окрестности частоты 1.5 ГГц. Благодаря этому
действительная часть входного сопротивления
=45. Из рис. 17
видно, что использование двухпроводного СИ приводит к появлению дополнительного
параллельного резонанса в окрестности частоты 1.5 ГГц. Благодаря этому
действительная часть входного сопротивления
![]() имеет всплеск
в этом диапазоне, причем его величина зависит от длины
имеет всплеск
в этом диапазоне, причем его величина зависит от длины ![]() .
.
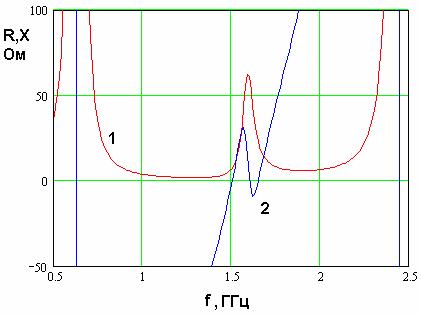
Рис. 17. Частотная зависимость входного сопротивления полуволновой КСА с двухпроводными СИ
На рис. 18 показаны зависимости от длины ![]() параметров
параметров
![]() и
и ![]() (кривые 1 и 2
соответственно) на частоте параллельного резонанса
(кривые 1 и 2
соответственно) на частоте параллельного резонанса ![]() . Также на рис. 19
показана зависимость резонансной частоты
. Также на рис. 19
показана зависимость резонансной частоты ![]() от параметра
от параметра ![]() . Отметим, что частота
. Отметим, что частота ![]() определялась как частота, на которой
сопротивление
определялась как частота, на которой
сопротивление
![]() достигает
максимума.
достигает
максимума.
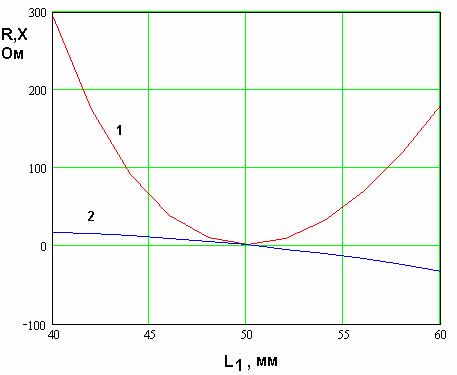
Рис. 18. Зависимость входного
импеданса полуволновой КСА с двухпроводными СИ от параметра ![]()
Из рис. 18 видно, что
функция ![]() имеет минимум при
имеет минимум при ![]() , причем в точке
минимума
, причем в точке
минимума ![]() =0. При удалении от экстремума
действительная часть входного сопротивления быстро растет и совпадает со
стандартным значением в 50 Ом в двух точках. В одной из них
=0. При удалении от экстремума
действительная часть входного сопротивления быстро растет и совпадает со
стандартным значением в 50 Ом в двух точках. В одной из них ![]() , а в другой
, а в другой ![]() . Наличие точки с нулевым значением
. Наличие точки с нулевым значением ![]() можно легко объяснить
следующим образом. Исходная КСА с однопроводными СИ представляет собой
закороченный с двух сторон полуволновый резонатор. Токи, текущие вдоль
проводников такого резонатора, обращаются в нуль в середине проводника. Поэтому
входное сопротивление КСА в этой точке равно бесконечности. В КСА с
двухпроводными СИ длиной
можно легко объяснить
следующим образом. Исходная КСА с однопроводными СИ представляет собой
закороченный с двух сторон полуволновый резонатор. Токи, текущие вдоль
проводников такого резонатора, обращаются в нуль в середине проводника. Поэтому
входное сопротивление КСА в этой точке равно бесконечности. В КСА с
двухпроводными СИ длиной ![]() мы подключаемся к антенне в точке бесконечным
сопротивлением. Это сопротивление затем пересчитывается ко входу через
четвертьволновый отрезок двухпроводной линии передачи, что приводит к инверсии
входного сопротивления, которое на входе становится равным нулю.
мы подключаемся к антенне в точке бесконечным
сопротивлением. Это сопротивление затем пересчитывается ко входу через
четвертьволновый отрезок двухпроводной линии передачи, что приводит к инверсии
входного сопротивления, которое на входе становится равным нулю.
Мнимая часть входного
сопротивления
![]() обращается в
нуль при
обращается в
нуль при ![]() . Она положительна при
. Она положительна при ![]() и
отрицательна при
и
отрицательна при ![]() .
Назовем значение мнимой части сопротивления
.
Назовем значение мнимой части сопротивления
![]() на резонансной
частоте
на резонансной
частоте ![]() остаточной реактивностью.
остаточной реактивностью.
Обращает на себя внимание
довольно сильная зависимость резонансной частоты от длины
![]() (см. рис. 19).
Снижение частоты
(см. рис. 19).
Снижение частоты ![]() при
при ![]() может быть использовано для
уменьшения размеров антенны.
может быть использовано для
уменьшения размеров антенны.
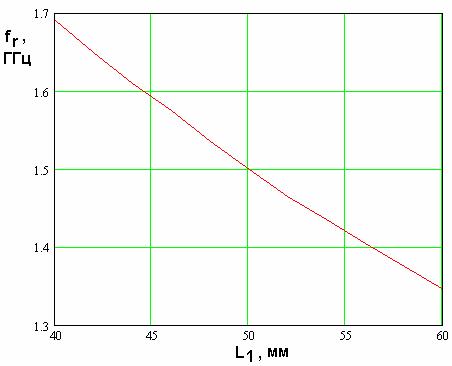
Рис. 19. Зависимость резонансной
частоты полуволновой КСА от параметра ![]()
На рис. 20 показана
частотная зависимость модуля коэффициента отражения ![]() от входа КСА, полученная
для антенны с параметрами указанными выше. Длина многопроводной линии передачи
от входа КСА, полученная
для антенны с параметрами указанными выше. Длина многопроводной линии передачи
![]() равна 45.5. С
помощью графика на рис. 20 можно оценить полосу согласования антенны. Если взять
в качестве критерия согласования условие
равна 45.5. С
помощью графика на рис. 20 можно оценить полосу согласования антенны. Если взять
в качестве критерия согласования условие ![]() , соответствующее коэффициенту стоячей
волны, меньшему 3, то мы получим полосу
, соответствующее коэффициенту стоячей
волны, меньшему 3, то мы получим полосу ![]() , равную 106 МГц.
, равную 106 МГц.
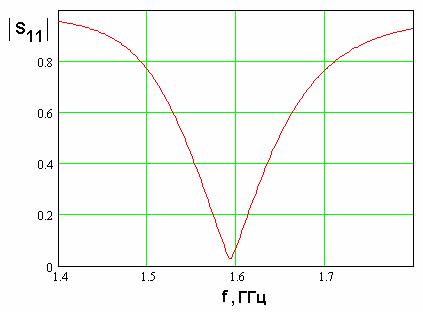
Рис. 20. Частотная зависимость модуля коэффициента отражения полуволновой КСА
Рассмотрим далее влияние
на характеристики антенны ширины проводников ![]() и зазора между ними
и зазора между ними ![]() . Они влияют на свойства КСА через
характеристические сопротивления собственных волн многопроводной линии передачи.
Так как мы рассматриваем двухпроводный СИ, то количество волн равно двум. Как
отмечалось выше, эти волны принято называть четной и нечетной. Обозначим их
характеристические импедансы через
. Они влияют на свойства КСА через
характеристические сопротивления собственных волн многопроводной линии передачи.
Так как мы рассматриваем двухпроводный СИ, то количество волн равно двум. Как
отмечалось выше, эти волны принято называть четной и нечетной. Обозначим их
характеристические импедансы через
![]() .
.
На рис. 21 показана
частотная зависимость модуля коэффициента отражения ![]() . Кривые 1 – 3 получены
при разных
. Кривые 1 – 3 получены
при разных ![]() . Геометрические размеры выбирались таким
образом, чтобы сопротивление
. Геометрические размеры выбирались таким
образом, чтобы сопротивление
![]() менялось
относительно слабо, а основные изменения происходили в
менялось
относительно слабо, а основные изменения происходили в ![]() .
В этом случае мы можем анализировать влияние на антенну характеристического
сопротивления двухпроводной линии передачи, соединяющей вход антенны и точку
возбуждения СИ. Отметим, что в силу неравенства
.
В этом случае мы можем анализировать влияние на антенну характеристического
сопротивления двухпроводной линии передачи, соединяющей вход антенны и точку
возбуждения СИ. Отметим, что в силу неравенства ![]() (см. формулу (13))
сопротивление двухпроводной линии, образованной проводниками, расположенными на
расстоянии
(см. формулу (13))
сопротивление двухпроводной линии, образованной проводниками, расположенными на
расстоянии ![]() друг от друга, с высокой
точностью равно
друг от друга, с высокой
точностью равно ![]() . Кривые 1 – 3 соответствуют следующим
значениям
. Кривые 1 – 3 соответствуют следующим
значениям ![]() :
: ![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]() . Им также соответствуют следующие значения
характеристических импедансов:
. Им также соответствуют следующие значения
характеристических импедансов: ![]() =60, 100, 150 Ом;
=60, 100, 150 Ом; ![]() =390,
385, 389 Ом.
=390,
385, 389 Ом.
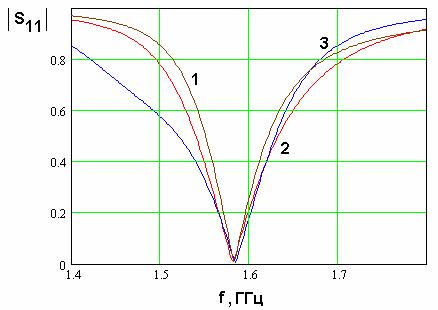
Рис. 21. Частотная зависимость модуля
коэффициента отражения полуволновой КСА при разных значениях параметров ![]()
Анализируя графики на рис. 21, мы можем сделать вывод о том, что повышение сопротивления двухпроводной линии расширяет полосу согласования КСА.
На рис. 22 также показана частотная зависимость модуля ![]() при разных значениях
при разных значениях ![]() . Отличие графиков на
рис. 22 от графиков на рис. 21 состоит в том, что они соответствуют КСА со
скомпенсированной остаточной реактивностью. Для этого ко входу антенны в
зависимость от знака
. Отличие графиков на
рис. 22 от графиков на рис. 21 состоит в том, что они соответствуют КСА со
скомпенсированной остаточной реактивностью. Для этого ко входу антенны в
зависимость от знака ![]() последовательно подключаются
компенсирующие емкость или индуктивность. Их величины выбираются таким образом,
чтобы мнимая часть входного сопротивления КСА равнялась нулю на частоте
последовательно подключаются
компенсирующие емкость или индуктивность. Их величины выбираются таким образом,
чтобы мнимая часть входного сопротивления КСА равнялась нулю на частоте ![]() . Качественно кривые на рис. 22 и 21 похожи.
Можно отметить некоторое (не очень большое) увеличение полосы согласования,
достигаемое с помощью компенсирующей реактивности.
. Качественно кривые на рис. 22 и 21 похожи.
Можно отметить некоторое (не очень большое) увеличение полосы согласования,
достигаемое с помощью компенсирующей реактивности.
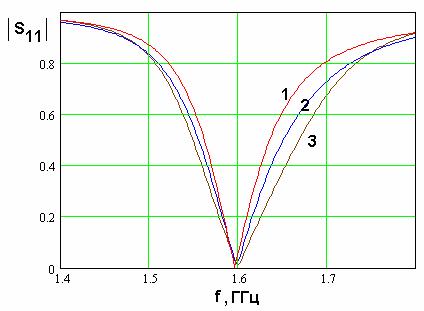
Рис. 22. Частотная зависимость модуля коэффициента отражения полуволновой КСА со скомпенсированной реактивностью входного импеданса
6. Электродинамическая модель четвертьволновой КСА
В этом разделе мы рассмотрим результаты исследования четвертьволновой КСА с помощью численного решения электродинамической задачи, которое позволяет достаточно строго учитывать все особенности геометрической структуры КСА. Численное решение осуществлялось с помощью программы электродинамического моделирования и проектирования ЭДЭМ («Электродинамика экранов из металла»).
В качестве первого шага рассмотрим модель КСА с однопроводными СИ. Она показана на рис. 23 а,б. Для оценки размеров КСА можно использовать сетку, показанную на рис. 23 а. Шаг сетки равен 10 мм. Основание КСА выполнено в виде крестообразного соединения двух металлических проводников, в которые включены два сосредоточенных источника с одинаковой по модулю амплитудой и сдвигом фазы на 900.
а б
Рис. 23. Модель четвертьволновой КСА с однопроводными СИ
На рис. 24 показаны частотные зависимости действительной и мнимой частей
входного сопротивления КСА. Им соответствуют кривые 1 и 2. Графики получены для
следующих параметров КСА: радиус ![]() , ширина проводника
, ширина проводника ![]() , высота антенны
, высота антенны ![]() , угол намотки спирали
, угол намотки спирали ![]() . Видно, что действительная часть входного
сопротивления на частоте резонанса (
. Видно, что действительная часть входного
сопротивления на частоте резонанса (![]() ) равна 3 Ом, что весьма
далеко от значения характеристического сопротивления стандартной линии передачи.
) равна 3 Ом, что весьма
далеко от значения характеристического сопротивления стандартной линии передачи.
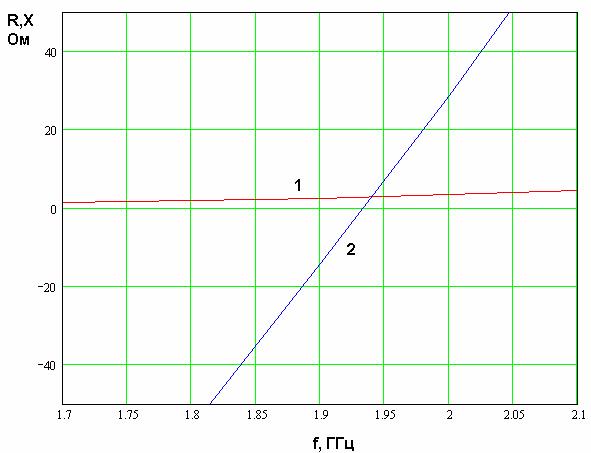
Рис. 24. Частотная зависимость входного импеданса четвертьволновой КСА с однопроводными СИ
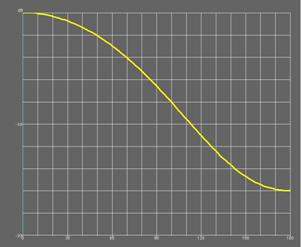
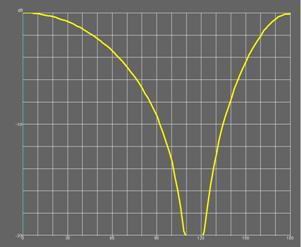
а б
Рис. 25. Диаграмма направленности (а) и коэффициент эллиптичности (б) четвертьволновой КСА с однопроводными СИ
На рис. 25 а,б показаны диаграмма направленности антенны по мощности и ее
коэффициент эллиптичности в зависимости от угла места
![]() , полученные на
частоте 1.7 ГГц. Угол
, полученные на
частоте 1.7 ГГц. Угол ![]() отсчитывается от оси 0z, которая совпадает с осью КСА. Характеристики КСА не зависят от
азимутального угла
отсчитывается от оси 0z, которая совпадает с осью КСА. Характеристики КСА не зависят от
азимутального угла ![]() . Коэффициент эллиптичности определяется в
ЭДЭМ через отношение осей эллипса поляризации. По этому параметру мы можем
судить только о близости поляризации излучения к круговой, но не имеем
информации о типе круговой поляризации (правая или левая круговая).
. Коэффициент эллиптичности определяется в
ЭДЭМ через отношение осей эллипса поляризации. По этому параметру мы можем
судить только о близости поляризации излучения к круговой, но не имеем
информации о типе круговой поляризации (правая или левая круговая).
Из рис. 25 а видно, что КСА обладает направленностью. Она имеет выраженный
максимум излучения в направлении оси 0z.
Поляризация излучения в этом направлении – правая круговая. Возможность создания
направленного излучения с помощью КСА является одним из их достоинств. Отметим
также, что при от осевого направления коэффициент эллиптичности излучения падает
и при некотором значении угла ![]() обращается в нуль. Затем он вновь растет до
нулевого значения (в децибелах), которое достигается при
обращается в нуль. Затем он вновь растет до
нулевого значения (в децибелах), которое достигается при ![]() .
При переходе коэффициента эллиптичности через нуль изменяется тип поляризации.
Если при малых углах
.
При переходе коэффициента эллиптичности через нуль изменяется тип поляризации.
Если при малых углах ![]() она была правой круговой, то при больших
углах она становится левой круговой поляризацией.
она была правой круговой, то при больших
углах она становится левой круговой поляризацией.
Анализ простой КСА с однопроводными СИ подтверждает актуальность задачи увеличения входного сопротивления антенны. Рассмотрим далее три КСА с трехпроводными СИ, которые показаны на рис. 26 а-в.
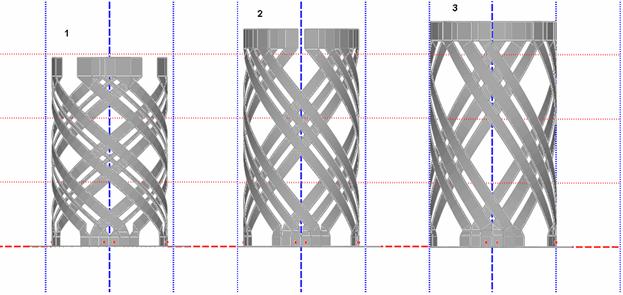
а б в
Рис. 26. Модели четвертьволновых КСА с трехпроводными СИ
Представленные модели КСА отличаются геометрическими размерами. Они представлены в табл. 1.
Табл. 1. Геометрические размеры КСА
|
|
w |
w1 |
s |
R |
m |
h |
|
|
1 |
0.5 |
1.6 |
0.9 |
9 |
0.5 |
29 |
42 |
|
2 |
1.2 |
1.6 |
0.9 |
9 |
0.4 |
33 |
54.6 |
|
3 |
2 |
1.6 |
0.9 |
10 |
0.3 |
35 |
67.5 |
Через
![]() обозначена
ширина внешнего проводника, через
w1 ширина внутреннего проводника, s – расстояние между ними, R – радиус КСА, h – ее высота, m – число витков спирали. В первом столбце табл. 1
приведены номера моделей КСА. Они соответствуют рис. 26 а-в.
обозначена
ширина внешнего проводника, через
w1 ширина внутреннего проводника, s – расстояние между ними, R – радиус КСА, h – ее высота, m – число витков спирали. В первом столбце табл. 1
приведены номера моделей КСА. Они соответствуют рис. 26 а-в.
На рис. 27 показано распределение электрических токов на проводниках КСА, которое позволяет качественно оценивать процессы, происходящие в антенне.
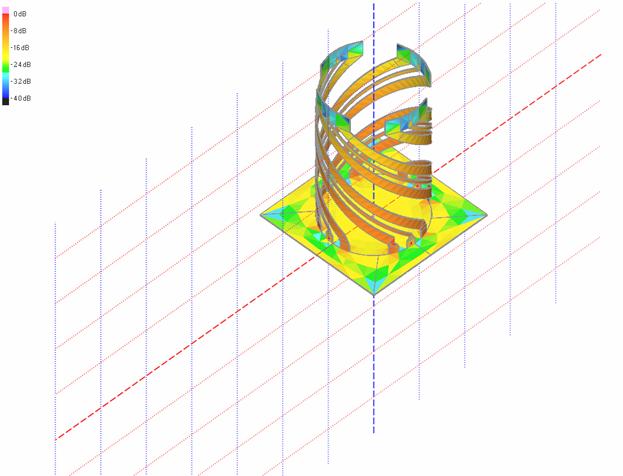
Рис. 27. Распределение электрических токов на проводниках КСА
Рассмотрим в качестве первого шага количественного анализа частотные зависимости
действительной и мнимой частей входного импеданса КСА, которые показаны на рис.
28. Они построены для модели номер 2. Кривая 1 соответствует действительной
части, а кривая 2 мнимой. Видно, что действительная часть входного
сопротивления резко выросла по сравнению с КСА с однопроводными СИ, что
доказывает высокую эффективность предложенного способа коррекции импедансных
характеристик антенны. Можно также отметить, что качественно частотная
характеристика входного сопротивления, полученная с помощью численного решения,
ведет себя аналогично решению на основе феноменологической модели (см. рис. 10).
На рабочей частоте 1.6 ГГц мы можем наблюдать последовательный резонанс. Имеются
также два параллельных резонанса, обеспечивающих рост действительной части
сопротивления. Оценивая полосу согласования четвертьволновой КСА, можно
отметить, что антенна достаточно узкополосна. Об этом говорит также зависимость
модуля коэффициента отражения от входа КСА, представленная на рис. 29. Видно,
что полоса согласования по критерию ![]() примерно равна 40 МГц.
примерно равна 40 МГц.
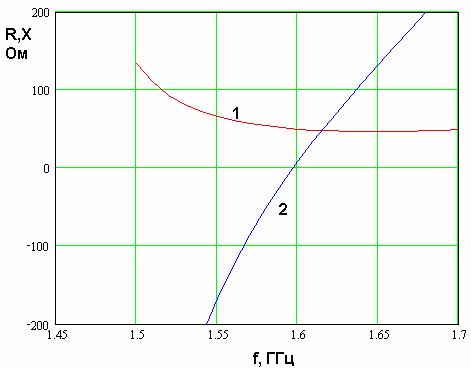
Рис. 28. Частотная зависимость входного импеданса четвертьволновой КСА
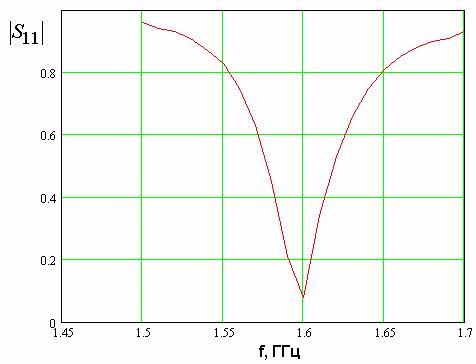
Рис. 29. Частотная зависимость модуля коэффициента отражения КСА
На рис. 30-32 представлены диаграммы направленности, соответствующие моделям 1-3, на частоте 1.6 ГГц. Видно, что они отличаются степенью направленности, которую удобно характеризовать уровнем излучения «назад». Он минимален для модели номер 2. Преимущественно направленность зависит от угла намотки спирали, который имеет оптимальное значение равное 54.60.
На рис. 33 показана зависимость коэффициента эллиптичности второй модели от угла ![]() . Она мало отличается от аналогичной
зависимости, полученной для КСА с однопроводными СИ.
. Она мало отличается от аналогичной
зависимости, полученной для КСА с однопроводными СИ.
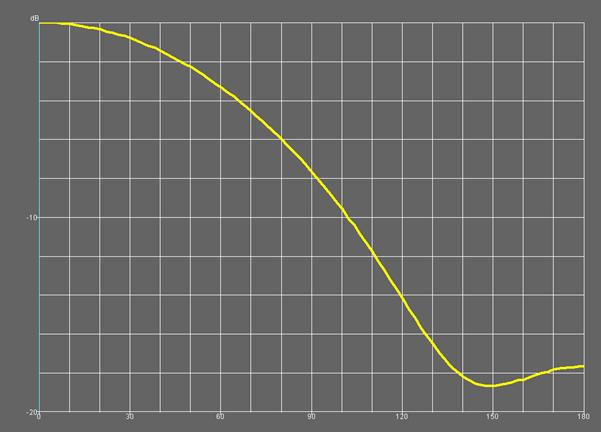
Рис. 30. Диаграмма направленности модели 1 четвертьволновой КСА
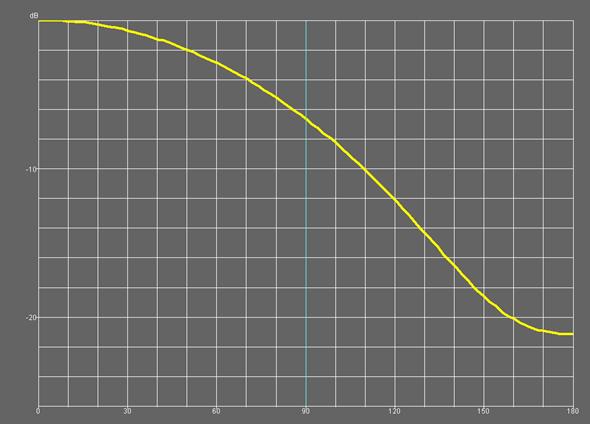
Рис. 31. Диаграмма направленности модели 2 четвертьволновой КСА
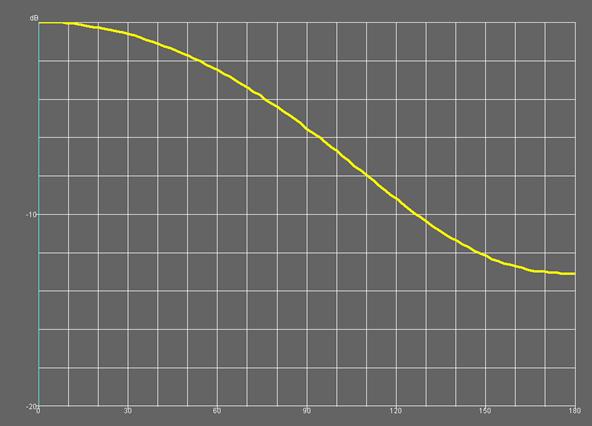
Рис. 32. Диаграмма направленности модели 3 четвертьволновой КСА
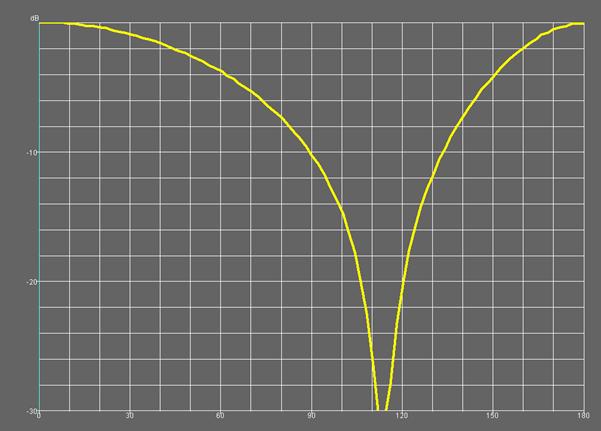
Рис. 33. Коэффициент эллиптичности модели 2
7. Электродинамическая модель полуволновой КСА
На первом этапе изучалась построенная с помощью программы ЭДЭМ модель полуволновой КСА с однопроводными СИ. Она показана на рис. 34 а,б. Антенна имеет основание в виде металлического диска. СИ возбуждаются четырьмя сосредоточенными источниками с одинаковыми амплитудами и сдвигом фаз на 900, которые необходимы для создания излучения с круговой поляризацией.
На рис. 35 представлены частотные зависимости параметров ![]() для КСА со следующими
размерами:
для КСА со следующими
размерами: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() - радиус КСА. Кривые 1 и 2, как и
раньше, соответствуют действительной и мнимой частям входного импеданса. Из рис.
35 можно сделать вывод о том, что у полуволновой КСА с одиночными СИ
действительная часть импеданса
- радиус КСА. Кривые 1 и 2, как и
раньше, соответствуют действительной и мнимой частям входного импеданса. Из рис.
35 можно сделать вывод о том, что у полуволновой КСА с одиночными СИ
действительная часть импеданса ![]() не столь мала, как в
случае четвертьволновой КСА. На резонансной частоте она равна 25 Ом, что меньше,
чем стандартное значение в 50 Ом, но разница между ними не очень значительна.
Она может быть устранена с помощью известных в СВЧ технике трансформаторов
сопротивлений.
не столь мала, как в
случае четвертьволновой КСА. На резонансной частоте она равна 25 Ом, что меньше,
чем стандартное значение в 50 Ом, но разница между ними не очень значительна.
Она может быть устранена с помощью известных в СВЧ технике трансформаторов
сопротивлений.
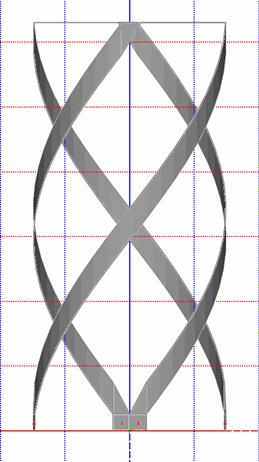
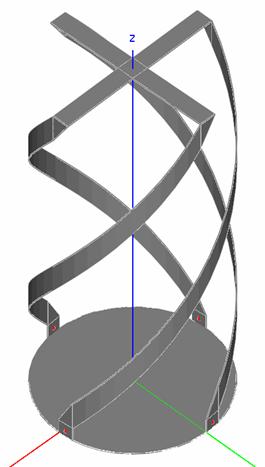
а б
Рис. 34. Модель полуволновой КСА
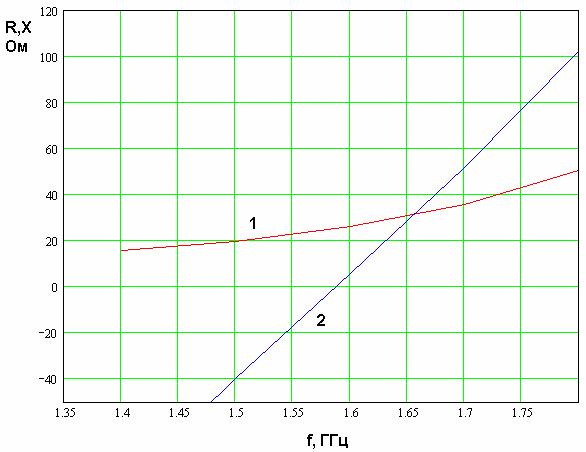
Рис. 35. Частотная зависимость входного импеданса полуволновой КСА
При уменьшении радиуса
полуволновой КСА действительная часть входного сопротивления уменьшается. Этот
вывод можно сделать из рис. 36, на котором показана зависимость сопротивления
![]() от радиуса
КСА. Другие параметры КСА совпадают с при веденными выше.
от радиуса
КСА. Другие параметры КСА совпадают с при веденными выше.
Таким образом, мы можем сделать вывод о том, что необходимость применения многопроводных СИ при проектировании полуволновых КСА в виде проводников, размещенных в свободном пространстве, не столь очевидна, как в случае четвертьволновых антенн. Исключение составляют ситуации, в которых имеются ограничения на размеры устройства, заставляющие уменьшать его диаметр.
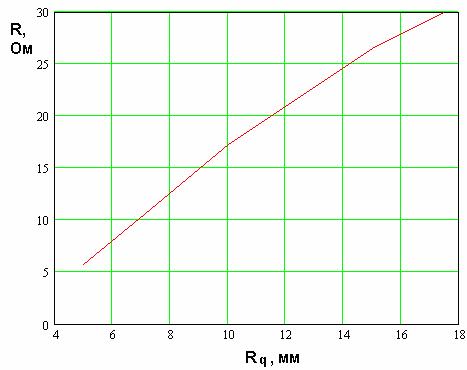
Рис. 36. Зависимость действительной части входного импеданса от радиуса КСА
Актуальность использования предлагаемого в работе технического решения повышается в тех случаях, когда антенна размещается на поверхности диэлектрического цилиндра. Такое изменение конструкции КСА бывает часто необходимым с точки зрения выполнения требований к механической прочности устройства. Появление диэлектрика весьма существенно сказывается на входном сопротивлении антенны. Анализ КСА с диэлектрическим каркасом не может быть проведена с помощью программы ЭДЭМ. Поэтому мы использовали систему HFSS, в основе которой лежит решение уравнений электродинамики методом конечных элементов.
На рис. 37а,б показана модель полуволновой КСА, построенная в системе HFSS, и зависимость действительной и мнимой частей ее входного импеданса от частоты. Размеры и параметры диэлектрика показаны на рис. 37а.
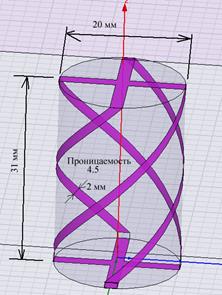
а б
Рис. 37. Модель полуволновой КСА в системе HFSS (а) и частотная зависимость ее входного сопротивления (б)
Из рис. 37б видно, что
применение диэлектрических материалов в конструкции КСА существенно снижает ее
входное сопротивление (до единиц Ом). Такое поведение сопротивление
![]() подтверждает
актуальность применения КСА с многопроводными СИ.
подтверждает
актуальность применения КСА с многопроводными СИ.
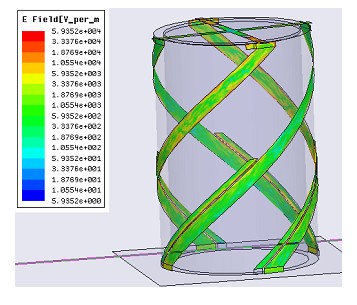
Рис. 38. Модель полуволновой КСА с двухпроводными СИ в системе HFSS
Модель полуволновой КСА с двухпроводными СИ была построена в системе HFSS. Она показана на рис. 38. На нем также показано распределение модуля напряженности электрических токов, текущих по проводникам КСА. Исследуемая антенна имела следующие параметры:
· внешний диаметр КСА – 30
· внутренний диаметр – 26
· высота – 44
· проницаемость диэлектрика – 4.5
· угол потерь – 0.002
· ширина длинного проводника – 3.9
· ширина короткого проводника – 1.6
· зазор между проводниками – 0.37
· угол поворота проводника – 180 град.
· длина длинного проводника – 65.44.
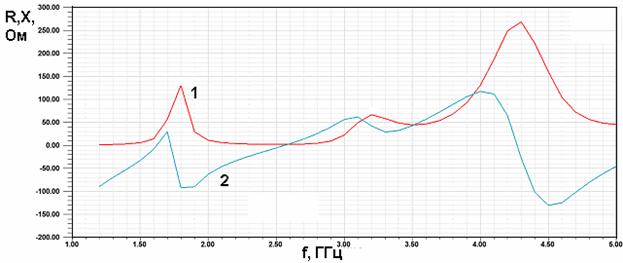
Переменным параметром является длина короткого проводника. На рис. 39 а-в показаны частотные зависимости действительной и мнимой частей входного импеданса КСА. Рис. 39 а-в получены для разных длин короткого проводника: 38.9, 32.59, 26.27.
Из рис. 39 а-в видно, что качественно поведение входного импеданса совпадает с предсказанным феноменологической моделью. На частотах 3 и 0.6 ГГц наблюдаются два параллельных резонанса, которые соответствуют резонансам КСА с однопроводными СИ. Между ними находится дополнительный параллельный резонанс, обусловленный присутствием второго (короткого) проводника. Величина действительной части входного импеданса на частоте дополнительного резонанса зависит от длины короткого проводника. Лучшее согласование наблюдается, когда она равна 38.9.
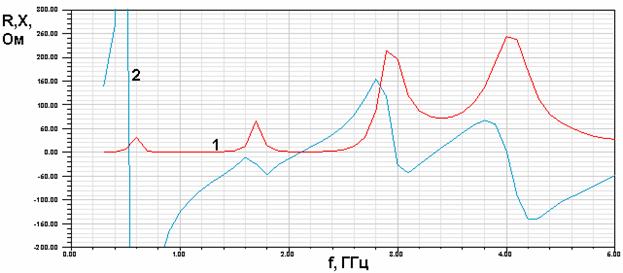
а
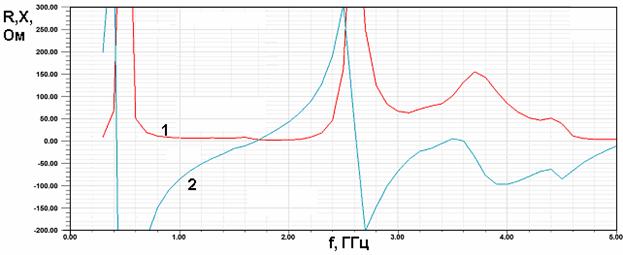
б
в
Рис. 39. Частотная зависимость входного импеданса полуволновой КСА при разной длине короткого проводника
8. Экспериментальное исследование многопроводных КСА
В этом разделе будут представлены результаты экспериментального исследования ряда КСА с многопроводными СИ, которые были разработаны в МКБ «Компас» для использования в приемниках систем спутниковой навигации.
На рис. 40 показана фотография четвертьволновой КСА с трехпроводными КСА. Экспериментально также исследовалась КСА с двухпроводными СИ. СИ выполнялись в виде полосковых проводников, расположенных на тонкой диэлектрической основе, которая сворачивалась в цилиндр, формируя систему из четырех СИ.

Рис. 40. Фотография макета четвертьволновой КСА с трехпроводными СИ
КСА устанавливалась на печатной плате со стороны ее металлического экрана. На противоположной стороне платы располагается схема питания КСА, которая представляет собой микрополосковую схему, имеющую четыре выхода, в виде металлических проводников, выведенных через экран. К ним присоединялись центральные проводники СИ. Другие проводники соединялись с экраном полосковой схемы.
Схема питания при работе антенны на передачу выполняет функцию формирования четырех напряжений, имеющих одинаковые амплитуды и сдвинутые по фазе на ±90 градусов друг относительно друга. В зависимости от знака фазового сдвига КСА излучает волны левой или правой круговой поляризаций. Схема питания может иметь разную структуру. В ходе экспериментов использовались схемы питания на основе реактивных делителей мощности и на основе балансных делителей мощности. В качестве балансных делителей применялись микросхемы серии QCN. Достоинством балансного делителя является согласование и развязка боковых плеч, которые исключают взаимодействие выходов схемы питания из-за рассогласования входов антенны. К недостаткам таких делителей относятся потери мощности, которые могут достигать 0.7-0.8 дБ на одну микросхему.
Реактивные делители мощности не имеют столь больших потерь, но их боковые плечи не согласованы и не развязаны. С одной стороны, это создает определенные сложности, которые обусловлены тем, что при рассогласовании входов антенны отраженные от них волны через схему питания поступают на ее соседние выходы. При этом амплитуды и фазы волн на этих выходах отличаются от оптимальных, что, в первую очередь, снижает коэффициент эллиптичности КСА. С другой стороны, схема питания на реактивных делителях мощности может улучшить согласование антенны, как это показано в работе [9]. Выбор типа схемы питания зависит от конкретных технических требований к антенне.
На рис. 41 представлена фотография, сделанная с экрана панорамного измерителя коэффициента стоячей волны (КСВ). Она показывает частотную зависимость КСВ антенны с трехпроводными СИ. Видно, что на центральной частоте, которая равна 1.59 ГГц антенна имеет КСВ равный 1.06, то есть она очень хорошо согласована. Это говорит о том, что применение многопроводных СИ действительно позволяет добиться согласования КСА с 50-омной линией передачи. Представленный образец КСА согласован по уровню КСВ=1.5 в полосе 1.572-1.62 ГГц. Такой полосы согласования достаточно для приема сигналов систем GPS и ГЛОНАС, которые излучаются в диапазоне 1.575-1.615 ГГц (так называемый диапазон L1).
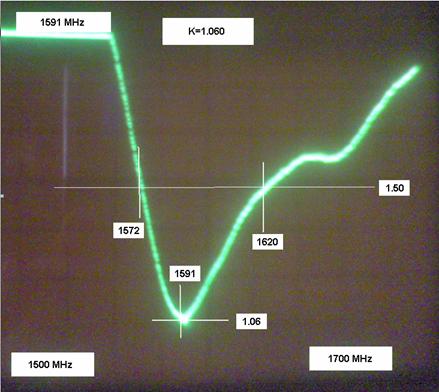
Рис. 41. Частотная зависимость КСВ четвертьволновой КСА
Для относительно узкополосных антенн, к которым относится четвертьволновая КСА, важным показателем качества является ее коэффициент усиления (КУ). Следует отметить, что для узкополосных антенн важное значение имеют тепловые потери, влияние которых не позволяет использовать КСВ в качестве единственного критерия эффективности излучения в свободное пространство.
Измерения КУ проводились по стандартной методике путем измерения коэффициента
передачи ![]() в тракте, включающем передающую
антенну, свободное пространство и приемную антенну. В качестве передающей
антенны использовалась широкополосная спиральная антенна. Если КУ эталонной
антенны известен, то, вычисляя разницу между коэффициентами передачи (выражены в
децибелах), которые обеспечивают исследуемая и эталонная антенны, можно найти КУ
исследуемой антенны. На практике критерием качества функционирования КСА
является близость ее коэффициента передачи к
в тракте, включающем передающую
антенну, свободное пространство и приемную антенну. В качестве передающей
антенны использовалась широкополосная спиральная антенна. Если КУ эталонной
антенны известен, то, вычисляя разницу между коэффициентами передачи (выражены в
децибелах), которые обеспечивают исследуемая и эталонная антенны, можно найти КУ
исследуемой антенны. На практике критерием качества функционирования КСА
является близость ее коэффициента передачи к ![]() эталонной антенны. В
качестве эталонной антенны применялась большая полуволновая КСА, которая имеет
КУ на уровне лучших антенн, используемых в системах спутниковой навигации.
эталонной антенны. В
качестве эталонной антенны применялась большая полуволновая КСА, которая имеет
КУ на уровне лучших антенн, используемых в системах спутниковой навигации.
На рис. 42 представлены частотные зависимости коэффициента передачи
четвертьволновых КСА с двухпроводными СИ. Кривые 1,2 соответствуют КСА с разными
параметрами. Кривая 3 соответствует эталонной антенне. Мы можем сделать вывод о
том, что разработанная КСА имеет максимальное значение ![]() , примерно на 1 дБ меньшее, чем у
эталонной антенны.
, примерно на 1 дБ меньшее, чем у
эталонной антенны.
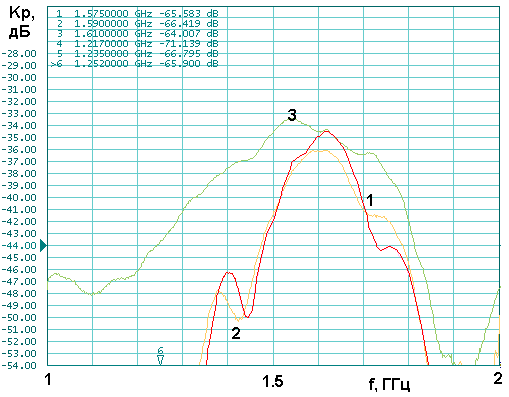
Рис. 42. Частотная зависимость коэффициента передачи четвертьволновой КСА с двухпроводными СИ
Снижение
![]() можно
объяснить существенным сужением полосы рабочих частот, то есть ростом
добротности антенны. Рост добротности, эквивалентный снижению излучающей
способности КСА, всегда сопровождается ростом тепловых потерь.
можно
объяснить существенным сужением полосы рабочих частот, то есть ростом
добротности антенны. Рост добротности, эквивалентный снижению излучающей
способности КСА, всегда сопровождается ростом тепловых потерь.
На рис. 43 показаны частотные зависимости коэффициента передачи четвертьволновых КСА с трехпроводными СИ. Кривые 1 - 3 соответствуют антеннам с разными размерами проводников, а кривая 4 получена для эталонной антенны. Оптимальной настройке КСА соответствует кривая 2. КСА с трехпроводными СИ более узкополосна, чем антенна с двухпроводными СИ. Также ее коэффициент передачи примерно на 0.5 дБ ниже.
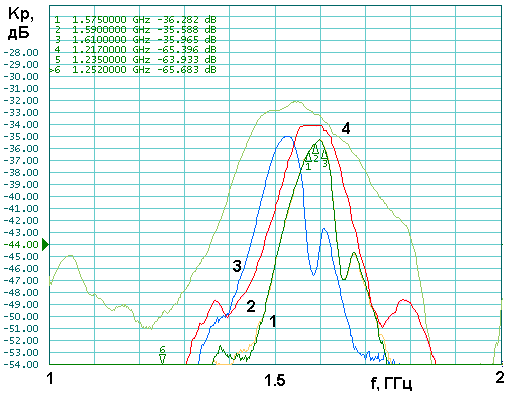
Рис. 43. Частотная зависимость коэффициента передачи четвертьволновой КСА с трехпроводными СИ
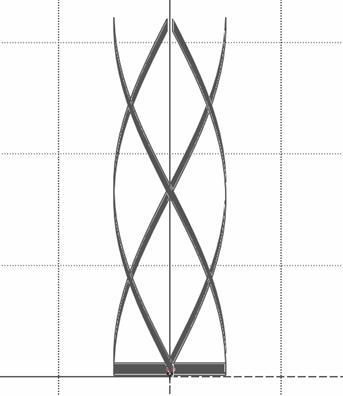
Полуволновая КСА с двухпроводными СИ была реализована в виде тонкой пленки с
печатными проводниками, расположенной на поверхности диэлектрического конуса
(см. рис. 44). В качестве диэлектрика использовался стеклотекстолит с
диэлектрической проницаемостью
![]() около 5.
Исследовались две антенны, отличающиеся рабочими частотами. Одна антенна
предназначена для работы в упомянутом выше диапазоне
около 5.
Исследовались две антенны, отличающиеся рабочими частотами. Одна антенна
предназначена для работы в упомянутом выше диапазоне ![]() , а другая в диапазоне
, а другая в диапазоне ![]() : 1.235-1.252 ГГц.
: 1.235-1.252 ГГц.
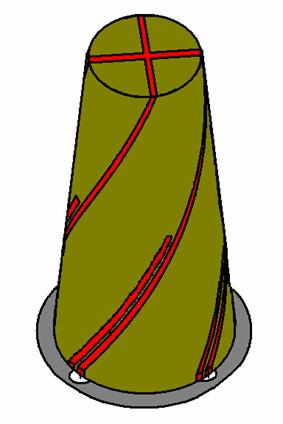
Рис. 44. Конструкция макета конической полуволновой КСА с двухпроводными СИ
На рис. 45 – 48 показаны полученные экспериментально характеристики полуволновых
КСА. На рис. 45 и 46 представлены частотные зависимости коэффициента передачи ![]() . На рис. 45 кривая 1
соответствует исследуемой КСА, кривая 2 эталонной антенне. На рис. 46 кривые 1 и
2 получены для КСА с разными размерами проводников, а кривая 3 соответствует
эталонной антенне.
. На рис. 45 кривая 1
соответствует исследуемой КСА, кривая 2 эталонной антенне. На рис. 46 кривые 1 и
2 получены для КСА с разными размерами проводников, а кривая 3 соответствует
эталонной антенне.
Из рис. 45 видно, что в диапазоне ![]() разработанная КСА имеет
практически тот же КУ, что и эталонная антенна. Они также близки по полосе
рабочих частот.
разработанная КСА имеет
практически тот же КУ, что и эталонная антенна. Они также близки по полосе
рабочих частот.
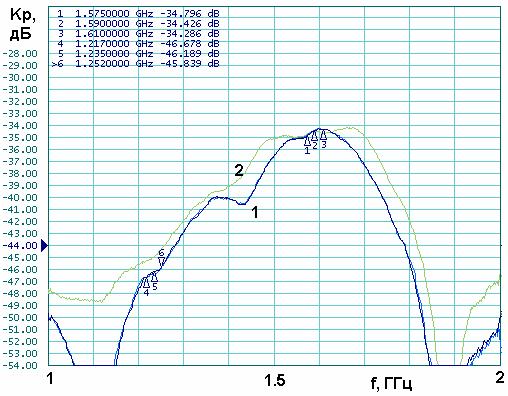
Рис. 45. Частотная зависимость
коэффициента передачи полуволновой КСА с двухпроводными СИ в диапазоне ![]()
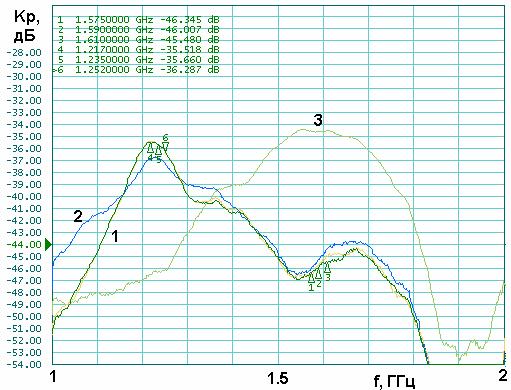
Рис. 46. Частотная зависимость
коэффициента передачи полуволновой КСА с двухпроводными СИ в диапазоне ![]()
В диапазоне ![]() исследуемая КСА примерно
на 1 дБ уступает эталонной, что можно объяснить снижением ее КУ за счет
уменьшения частоты.
исследуемая КСА примерно
на 1 дБ уступает эталонной, что можно объяснить снижением ее КУ за счет
уменьшения частоты.
На рис. 47 и 48 изображены полученные экспериментально диаграммы направленности
КСА в диапазонах ![]() и
и ![]() соответственно.
Диаграммы направленности измерены в плоскости, проходящей через ось антенны,
верхняя часть которой ориентирована в направлении
соответственно.
Диаграммы направленности измерены в плоскости, проходящей через ось антенны,
верхняя часть которой ориентирована в направлении
![]() . Видно, что
КСА в обоих диапазонах обладает направленными свойствами.
. Видно, что
КСА в обоих диапазонах обладает направленными свойствами.
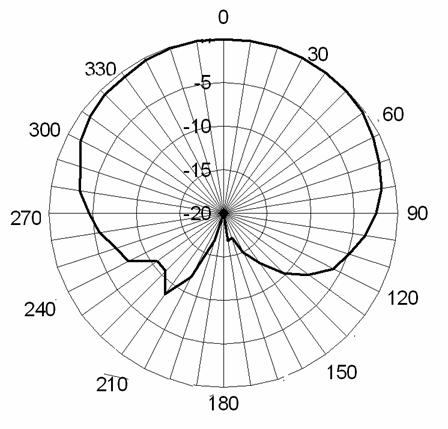
Рис. 47. Диаграмма направленности
полуволновой КСА в диапазоне ![]()
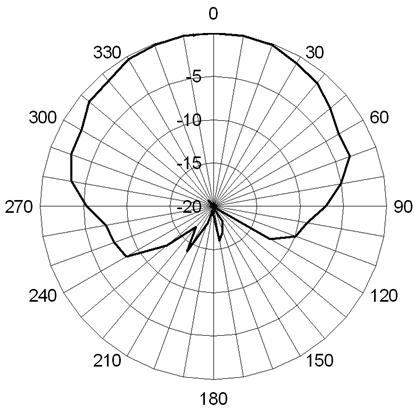
Рис. 48. Диаграмма направленности
полуволновой КСА в диапазоне
![]()
Литература
4. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высшая школа. 1988.
5. Сазонов В.П., Силин Р.А. Замедляющие системы. М.: Сов. Радио. 1966.
6. Неганов А.А., Яровой Г.П. Теория и применение устройств СВЧ. М.: Радио и связь. 2006.
7. Справочник по расчету и конструированию СВЧ полосковых устройств. Под ред. В.И. Вольмана. М.: Радио и связь. 1982.
8. Конструирование и расчет полосковых устройств. Под. ред. И.С. Ковалева. М.: Сов. Радио. 1974.
9. Банков С.Е., Давыдов А.Г., Курушин А.А. Проектирование многоэлементных антенн со сложными системами питания // EDA Express. 2007. №16. С.23.