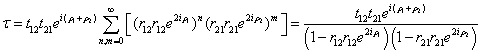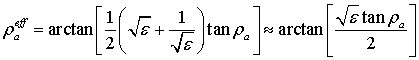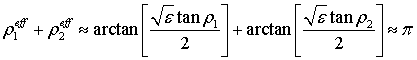УДК:537.876.2
Особенности формирования запрещённых зон в одномерных фотонных кристаллах большого контраста
М. В. Лазарев 1,2, А. М. Мерзликин 1
1 ИТПЭ РАН (Институт Теоретической и Прикладной Электродинамики Российской Академии Наук)
2 МФТИ – НИУ (Московский Физико-Технический Институт - Научно Исследовательский Университет)
Получена 6 июня 2011 г.
Аннотация. Обычно образование запрещенных зон в фотонных кристаллах (ФК) связывается с выполнением условия брэгговского отражения, когда длина оптического пути через элементарную ячейку порядка половины длины волны. Показано, что при большом контрасте значений адмитанса слоев, образующих одномерный ФК, возможно образование запрещённой зоны в случае, когда длина оптического пути через элементарную ячейку много меньше половины длины волны. Физическая реализация таких ФК возможна в СВЧ диапазоне. Дано качественное объяснение этого эффекта на основе понятия многопроходности. Выведено условие резонансного отражения, применимое к фотонным кристаллам большого контраста.
Ключевые слова: фотонные кристаллы, большой контраст проницаемостей, многопроходность.
Abstract. Usually, the formation of band gaps in photonic crystals (PCs) associated with the condition of Bragg reflection, when the optical path length through the unit cell size of half a wavelength. In this article we have shown that at high contrast admittance values of layers, forming a one-dimensional PC, there can be formed band gaps when the optical path length through the unit cell is much less than half the wavelength. Physical implementation of this PC available in the UHF range. Qualitative explanation of this effect is based on the multipass concept. We derive the condition for resonance reflection applicable to photonic crystals of a large contrast.
Keywords: photonic crystals, high contrast of permeability constant, multipass.
1. Введение.
В современной оптике большую роль играют периодические среды - фотонные кристаллы (ФК) [1]. В оптике это миниатюрные устройства порядка нескольких, иногда десятка длин волн. Что связано с тем, что характерный масштаб, период по порядку величины, совпадает с длинной волны. Именно в этом диапазоне часто в ФК возникают запрещенные зоны, играющие ключевую роль почти во всех приложениях.
В СВЧ длина волны в вакууме составляет десятки сантиметров и, ожидаемые приборы, использующие свойства запрещенных зон ФК, должны быть метровых размеров1. Однако область СВЧ обладает важным отличием от оптики – в СВЧ существуют материалы с большой диэлектрической проницаемостью (вплоть до 3500) [2] , что принципиально меняет ситуацию2. Рассмотрим условие формирования запрещенных в ФК. При малом контрасте диэлектрических проницаемостей, как показано в рамках теории возмущений [2], запрещенная зона формируется вокруг частоты, определяемой равенством
|
|
(1) |
где ![]() -- длина оптического пути по i-тому слою. Ширина этой
запрещенной зоны пропорциональна контрасту [2]
-- длина оптического пути по i-тому слою. Ширина этой
запрещенной зоны пропорциональна контрасту [2]
|
|
(2) |
Поскольку в оптике большинство материалов имеют проницаемости порядка нескольких единиц, то формулы (1) и (2) дают хорошую оценку. Заметим, что ширина запрещенной зоны возрастает с увеличением контраста. Использование теории возмущения при выводе (2) предполагает, что на краях запрещенной зоны условие брэгговского отражения почти выполняется.
Переход в СВЧ диапазон позволяет увеличивать контраст проницаемостей, мы должны наблюдать увеличение ширины запрещенной зоны, и рано или поздно, ситуация выходит за рамки теории возмущения. На возможное ограничение ширины запрещенной зоны указывает теория гомогенизации. Действительно, казалось бы оптически тонкие структуры могут быть описаны в рамках эффективной среды [3]. В этом случае никаких мезоскопичных эффектов, в том числе формирования запрещенных зон быть не может.
Настоящая работа посвящена исследованию предела нижней границы запрещенной зоны. Иными словами, насколько оптически и физически тонкой может быть структура, чтобы обладать запрещенной зоной? В частности возможно ли создание оптически тонких ФК?
Так как при одних и тех же ингредиентах одномерные фотонные кристаллы обладают наиболее широкой и глубокой запрещенной зоной [4]. Поэтому для поиска оптически тонких структур обладающих брэгговским отражением мы будем использовать периодические слоистые среды – то есть одномерный ФК, для описания которых использовался аппарат Т-матриц [5]. Для упрощения одной компонентой ФК взят вакуум, а в качестве второй - непоглощающий немагнитный диэлектрик.
2. Связь брэгговского отражения с формированием запрещенных зон фотонного кристалла малого контраста
Для ФК, период которого состоит из двух
слоев с проницаемостями ![]() и толщинами
и толщинами ![]() , дисперсионное уравнение дается известным
выражением [6]
, дисперсионное уравнение дается известным
выражением [6]
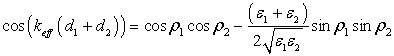 ,
,
где ![]() длина оптического
пути, нормированная на длину волны, в дальнейшем под оптической длинной мы
будем подразумевать именно эту безразмерную величину.
длина оптического
пути, нормированная на длину волны, в дальнейшем под оптической длинной мы
будем подразумевать именно эту безразмерную величину.
Существуют частоты,
при которых правая часть дисперсионного уравнения по модулю больше 2 (см. Рис. 1)
и, следовательно, ![]() имеет ненулевую мнимую часть
даже для непоглощающих материалов. Область таких частот образует запрещенную
зону. На графике пунктиром обозначен след
Т-матрицы для ФК из двух слоёв одинаковой толщины
имеет ненулевую мнимую часть
даже для непоглощающих материалов. Область таких частот образует запрещенную
зону. На графике пунктиром обозначен след
Т-матрицы для ФК из двух слоёв одинаковой толщины ![]() с
диэлектрическими проницаемостями равными
с
диэлектрическими проницаемостями равными ![]() и,
и, ![]() сплошной линией обозначен коэффициент прохождения волны через ФК из
12-ти таких слоёв, точками - мнимая часть волнового вектора. По горизонтальной
оси безразмерная частота (волновое число в вакууме умноженное на толщину слоя).
сплошной линией обозначен коэффициент прохождения волны через ФК из
12-ти таких слоёв, точками - мнимая часть волнового вектора. По горизонтальной
оси безразмерная частота (волновое число в вакууме умноженное на толщину слоя).
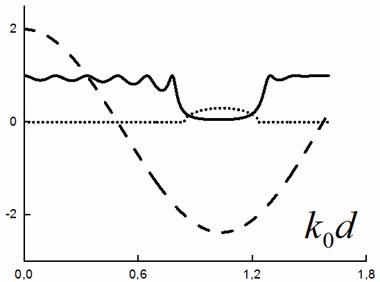
Рис. 1.
Пунктиром обозначен след Т-матрицы, сплошной линией обозначен коэффициент прохождения волны, точками - мнимая часть волнового вектора.
Как
указывалось во введении, в случае малого контраста ![]() низшая
по частоте запрещенная зона представляет собой узкий интервал частот вокруг
частоты
низшая
по частоте запрещенная зона представляет собой узкий интервал частот вокруг
частоты ![]() , определяемой условием
, определяемой условием
![]() .
.
То есть, для всех частот запрещенной зоны оптическая толщина периода порядка
|
(3) |
В случае малого контраста эта формула имеет простой физический смысл.
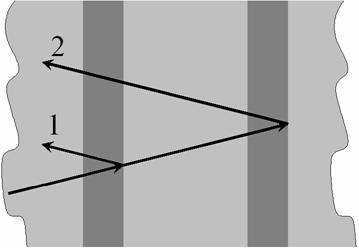
Рис 2.
На рисунке изображён ФК и падающая
на него волна, а также её отражение от слоёв с большим ![]() .
.
В
случае малого контраста в методе парциальных волн (схеме Эйри) достаточно
учесть лишь однократные отражения (см. Рис. 2). Действительно, в формуле (2)
видно, что ширина зоны пропорциональна коэффициенту отражения в первой степени.
При выполнении условия (3) оптическая толщина периода
будет равна ![]() , следовательно, отражённые волны 1 и 2
будут синфазными (так как оптический путь для 1-й волны равен нулю, а для 2-й
равен удвоенной оптической толщине -
, следовательно, отражённые волны 1 и 2
будут синфазными (так как оптический путь для 1-й волны равен нулю, а для 2-й
равен удвоенной оптической толщине - ![]() ), то есть возникает
резонансное усиление отражения – так называемое брэгговское отражение.
), то есть возникает
резонансное усиление отражения – так называемое брэгговское отражение.
3. Запрещенные зоны фотонного кристалла большого контраста
Рассмотрим, как меняется частота нижней границы запрещенной зоны и соответствующая ей оптическая толщина периода при увеличении контраста.
Для начала рассмотрим распространенный
случай, когда толщины слоев одинаковы ![]() . В этом случае (см. Рис. 3), частота нижней границы уменьшается и стремится
к нулю, а вот соответствующая оптическая толщина (см. Рис. 4) выходит на
константу. Действительно, при больших
. В этом случае (см. Рис. 3), частота нижней границы уменьшается и стремится
к нулю, а вот соответствующая оптическая толщина (см. Рис. 4) выходит на
константу. Действительно, при больших ![]() частота
уменьшается как
частота
уменьшается как ![]() , то есть оптическая длина слоя
с большей проницаемостью
, то есть оптическая длина слоя
с большей проницаемостью ![]() остается постоянной. Таким
образом, когда толщины слоев одинаковы, достичь брэгговского отражения на оптически
тонких структурах не удается (Рис. 4).
остается постоянной. Таким
образом, когда толщины слоев одинаковы, достичь брэгговского отражения на оптически
тонких структурах не удается (Рис. 4).
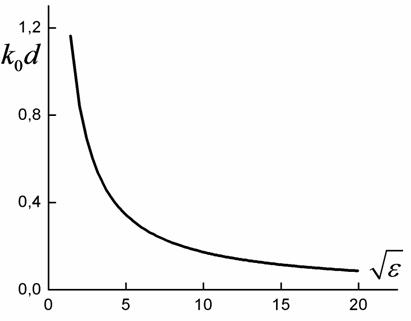
Рис. 3.
На графике показана зависимость минимального волнового числа от контраста, при котором появляется запрещённая зона. По оси Х- контраст (отношение адмитансов).

Рис. 4.
На этом рисунке изображена зависимость оптической толщины от контраста для ФК из двух слоёв одинаковой толщины. Диэлектрическая проницаемость одного из слоев равна 1.
Однако,
данную структуру можно оптимизировать по соотношению толщин ![]() . При фиксированном контрасте оптическая
длина периода (для частоты соответствующей при данном контрасте границе
запрещенной зоны) существенно зависит от соотношения толщин слоев. Рассмотрим
систему из двух слоёв с фиксированой толщиной периода с диэлектрическими
проницаемостями
. При фиксированном контрасте оптическая
длина периода (для частоты соответствующей при данном контрасте границе
запрещенной зоны) существенно зависит от соотношения толщин слоев. Рассмотрим
систему из двух слоёв с фиксированой толщиной периода с диэлектрическими
проницаемостями ![]() =100
=100 ![]() =1 (см.
Рис. 5).
=1 (см.
Рис. 5).

Рис. 5
Зависимость оптической длины системы от толщины первого слоя при фиксированной толщине периода.
Численные расчеты показывают, что минимум оптической толщины достигается при условии
![]()
которое, как известно [1], соответствует максимальной ширине запрещенной зоны. Такой ФК мы будем называть оптимизированным.
Теперь рассмотрим зависимость минимальной оптической длины от контраста в оптимизированном фотонном кристалле. Расчеты показывают (см. Рис. 6), что по мере увеличения контраста оптическая длина периода становится значительно меньше единицы.
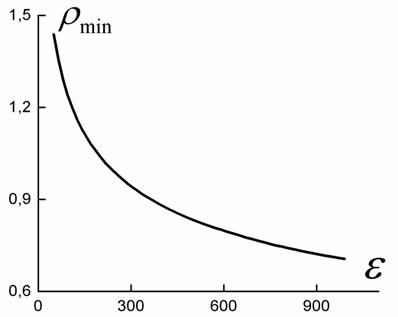
Рис. 6
На
графике изображена зависимость оптической длины оптимизированной системы от ![]() .
.
Можно показать аналитически, с помощью уравнения Рытова, как ведёт себя оптическая толщина периода при большом контрасте для оптимизованной системы у нижней границы первой запрещённой зоны. Для простоты будем считать, что диэлектрическая проницаемость второго слоя равна 1.
Так как система оптимизованна, то ![]()
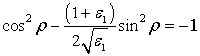
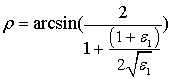
Разложив это в ряд Тейлора, получим:
![]() , где
, где
![]()
Отметим, что при
проницаемости второго материала ![]() оптическая длина
периода порядка 0.5, следовательно, в каждом из слоев отношение толщины слоя к
длине волны в нем всего порядка
оптическая длина
периода порядка 0.5, следовательно, в каждом из слоев отношение толщины слоя к
длине волны в нем всего порядка ![]() , то есть толщина каждого
слоя много меньше длины волны в нем, но не смотря на это, теория гомогенизации
даст некорректную оценку (см. Рис. 7). Для примера рассмотрим оптимизованную
систему из пяти периодов с
, то есть толщина каждого
слоя много меньше длины волны в нем, но не смотря на это, теория гомогенизации
даст некорректную оценку (см. Рис. 7). Для примера рассмотрим оптимизованную
систему из пяти периодов с ![]()
![]() и сравним точный расчёт коэффициента
прохождения для ФК с расчётом с помощбю теории гомонгенизации
и сравним точный расчёт коэффициента
прохождения для ФК с расчётом с помощбю теории гомонгенизации![]() .
.
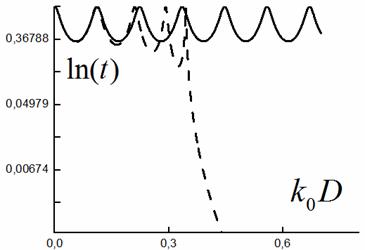
Рис. 7.
Зависимость коэффициента прохождения для данной системы в логорифмическом маштабе. Сплошная линия – коэффициент прохождения расчитанный с помощью теории гомонгенизации, пунктир – точное решение.
3. Многопроходность.
Таким
образом, мы показали, что при правильно подобранном соотношении толщин ![]() и
и ![]() ,
оптическая длина периода ФК с большим контрастом может быть значительно меньше
,
оптическая длина периода ФК с большим контрастом может быть значительно меньше ![]() .
.
В случае большого контраста нельзя рассматривать коэффициент прохождения как произведение коэффициентов прохождения каждого слоя (в силу эффекта много проходности), и получить условие формирования запрещённых зон в ФК с большим контрастом, аналогичное условию Брега, нельзя. Кроме того, так как коеффициентпрохождения слоя при увеличении диэлектрической проницаемости стремится к нулю, говорить о фазе коэффициента прохождения смысла нет.
Для объяснениявозникновения резонансного отражения от оптически тонких структур рассмотрим метод парциальных мод.
В
отличие от рассмотренного ранее случая малого контраста, когда можно пренебречь
многократным отражением, в случае большого контраста и небольших (в сравнении с
![]() ) оптических длинах3 можно пренебречь многократным
прохождением через границу раздела вакуума и диэлектрика. Действительно,
амплитуда остальных путей пропорциональна коэффициенту прохождения в слой с большим
) оптических длинах3 можно пренебречь многократным
прохождением через границу раздела вакуума и диэлектрика. Действительно,
амплитуда остальных путей пропорциональна коэффициенту прохождения в слой с большим
![]() в
некоторой степени. Например, рассмотрим луч, который отражается от последнего
слоя, и не будем учитывать биение внутри слоёв, а потом от первого слоя и так N
раз. Отношение его амплитуды к амплитуде насквозь прошедшей волны будет равно
в
некоторой степени. Например, рассмотрим луч, который отражается от последнего
слоя, и не будем учитывать биение внутри слоёв, а потом от первого слоя и так N
раз. Отношение его амплитуды к амплитуде насквозь прошедшей волны будет равно![]() , где n-количество
слоёв,
, где n-количество
слоёв, ![]() - коэффициенты прохождения на границе сред и отражения на границах с
вакуумом. Но поскольку таких путей много (их количество, очевидно,
увеличивается с ростом N), далее мы дадим численную оценку этим рассуждениям.
- коэффициенты прохождения на границе сред и отражения на границах с
вакуумом. Но поскольку таких путей много (их количество, очевидно,
увеличивается с ростом N), далее мы дадим численную оценку этим рассуждениям.
Оставшиеся пути имеют вид, представленный на рисунке 8.
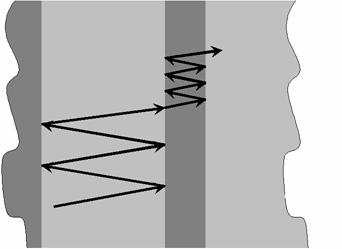
Рис.8
Метод парциальных волн для большого контраста.
Сравнивая с методом
парциальных волн в случае малого контраста, мы замечаем, что за счет
многократного прохождения по слою волна может «нагулять» большую эффективную оптическую
длину. Это явление принято называть многопроходностью. То есть, несмотря на
то, что ![]() , эффективная оптическая длина может быть
сравнима с
, эффективная оптическая длина может быть
сравнима с ![]() .
.
Найдем эту оптическую длину. Сумма всех оптических путей ![]() , не содержащих более одного перехода
через границу раздела между слоями (аналогичных представленным на Рис. 8),
будет равна
, не содержащих более одного перехода
через границу раздела между слоями (аналогичных представленным на Рис. 8),
будет равна
|
|
(4) |
где ![]() и
и ![]() -
соответственно коэффициенты отражения и прохождения на границе сред, а
-
соответственно коэффициенты отражения и прохождения на границе сред, а ![]() - оптические длины. Для удобства
изложения мы считаем, что волна падает не снаружи, а с левой внутренней границы
одного из слоев, что позволяет нам не учитывать дополнительный коэффициент
- оптические длины. Для удобства
изложения мы считаем, что волна падает не снаружи, а с левой внутренней границы
одного из слоев, что позволяет нам не учитывать дополнительный коэффициент ![]() .
.
Чтобы
понять насколько адекватна оценка (4), найдем вклад остальных путей. Учтём те
лучи, что бились во втором слое и вернулись опять в первый, соответствующий
коэффициент прохождения обозначим за ![]() . Суммарная амплитуда
этих лучей у полубесконечной стенки будет равна:
. Суммарная амплитуда
этих лучей у полубесконечной стенки будет равна:
![]() ,
,
где ![]() , тогда
, тогда 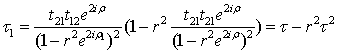 .
.
Аналогичным образом можно
учесть следующую поправку к ![]() . И таким образом мы
получим общее точное решение.
. И таким образом мы
получим общее точное решение.
 (5)
(5)
Если разложить ![]() в ряд Тейлора
по степеням
в ряд Тейлора
по степеням ![]() , то получим
, то получим ![]()
Как видно из (5), каждая следующая поправка меньше предыдущей в 4 раза. Поэтому для простой оценки мы возьмем только первый член, то есть «однократной многопроходности».
Отметим
важное свойство формулы (4), так же как и для случая малого контраста (когда
коэффициент прохождения есть просто произведение коэффициентов прохождения
через все границы) ![]() представляется в виде произведения
прохождения через отдельные слои
представляется в виде произведения
прохождения через отдельные слои
|
|
|
Таким образом ![]() , играет роль коэффициента прохождения и
его фазу, по аналогии со случаем малого контраста, мы будем считать эффективной
оптической длиной слоя
, играет роль коэффициента прохождения и
его фазу, по аналогии со случаем малого контраста, мы будем считать эффективной
оптической длиной слоя ![]() . После элементарных
преобразований получим
. После элементарных
преобразований получим
|
|
(5) |
Численные расчеты показывают (см. Рис. 9), что для эффективных оптических длин при возникновении запрещенной зоны выполняется брэгговского условие:
|
|
(6) |
Отметим, что в случае
малого контраста формула (5) переходит в ![]() и
условие (6) переходит в обыкновенное бреговское условие (3). Таким образом,
формулу (6) можно рассматривать как обобщенное бреговское условие.
и
условие (6) переходит в обыкновенное бреговское условие (3). Таким образом,
формулу (6) можно рассматривать как обобщенное бреговское условие.
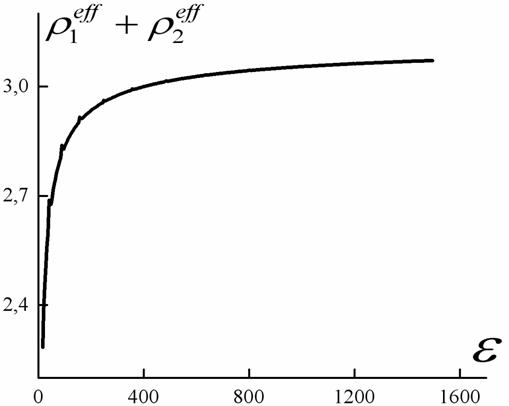
Рис. 9.
На графике показана зависимость суммы эффективных оптических толщин (6) от контраста, для частоты, соответствующей нижней границы запрещенной зоны.
Заключение.
В
работе рассмотрено формирование запрещенных зон в одномерном фотонном
кристалле, период которого состоит из двух слоев – вакуума и немагнитного
непоглощающего диэлектрика с большой диэлектрической проницаемостью ![]() .
.
Показано,
что если слои взять одинаковой толщины, то при увеличении ![]() частота нижней границы запрещенной зоны
стремится к нулю, но оптическая толщина соответствующая нижней границы
запрещенной зоны, стремится к константе, сравнимой с
частота нижней границы запрещенной зоны
стремится к нулю, но оптическая толщина соответствующая нижней границы
запрещенной зоны, стремится к константе, сравнимой с ![]() .
Однако, если оптимизировать толщины слоев, то удается достичь оптически тонких структур,
на которых наблюдаются запрещенные зоны.
.
Однако, если оптимизировать толщины слоев, то удается достичь оптически тонких структур,
на которых наблюдаются запрещенные зоны.
Для объяснения резонансного отражения от оптически тонких структур предложено явление многопроходности, на основании которого удалось обобщить брэгговское условие резонансного отражения на фотонные кристаллы с большим контрастом.
Работа выполнена при частичной финансовой поддержке РФФИ (проект № 10-02-90466-Укр_а).
Литература
1. G. S. Johnson and D. J. Joannopoulos, Photonic Crystals: The Road from Theory to Practice (Kluwer, Boston, 2002).
2. Вул.Б.М Вещества с высокой и сверхвысокой диэлектрической проницаемостью (УФН, 1967)
3. А.Ярив , П. Юх, Оптические волны в кристаллах (Мир, Москва, 1987).
4. W. Voigt Lehrbuch der Kristallphysik, Teubner, Berlin (1928), A. Reuss Berechnung der Fliebgrenze von Mischkristallen auf Grund der Plastizitatsbedingung fur rinkristalle, ZAMM (1929).
5. A.M. Merzlikin, A.P. Vinogradov. Opt. Comm. 259, 700 (2006).
6. M. Born, E. Wolf, Principles of Optics, sixth ed., Pergamon Press, New York, 1993.
7. Л.М. Бреховских, Волны в слоистых средах (Наука, Москва, 1973)
1 Отметим, что, вообще говоря, технологические и научные цели отличаются. С технологической точки зрения интерес представляют ФК наименьшего физического размера, в то время как с научной точки зрения основной интерес представляют изучение ФК наименьшей оптической длины.
2 В данной статье мы ограничимся рассмотрением диэлектрических структур, так как они обладают чёткими границами запрещённых зон.Однако, наибольший контраст диэлектрических проницаемостей наблюдается в металл-диелектрических структурах, но из-за поглощения выделить начало и конец запрещённой зоны очень трудно.Эта тема будет рассмотрена в следующей публикации.
3 Второе требование становится
очевидным, если рассмотреть слой, оптическая длина которого равна ![]() . В этом случае, не зависимо от адмитанса
этот слой прозрачен, его Т-матрица равна минус единичной и для корректной
оценки, вообще говоря, необходимо учитывать все пути которые проходят через
него, в том числе и те, которые многократно пересекают его границу.
. В этом случае, не зависимо от адмитанса
этот слой прозрачен, его Т-матрица равна минус единичной и для корректной
оценки, вообще говоря, необходимо учитывать все пути которые проходят через
него, в том числе и те, которые многократно пересекают его границу.
 .
.