УДК 621.372.852.1
УПРАВЛЯЕМЫЙ ЭЛЕКТРИЧЕСКИМ ПОЛЕМ ВОЛНОВОДНЫЙ ФИЛЬТР ШОЛЬЦА
А. И. Игнатов, А. М. Мерзликин
Институт Теоретической и Прикладной Электродинамики РАН, Москва
Получена 30 августа 2011 г.
Аннотация. Предложена схема управляемого волноводного оптического фильтра на основе планарного гофрированного волновода из электрооптического материала. Работа фильтра основана на управлении вырожденной запрещенной зоной, возникающей в результате связи ТЕ и ТМ мод благодаря наведенной внешним электрическим полем анизотропии материала волновода. С помощью метода связанных мод в приближении малой по сравнению с толщиной волновода амплитуды гофра и малой анизотропии рассчитаны характеристики вырожденной запрещенной зоны. Преимуществом предложенной конструкции управляемого фильтра является простота изготовления в сравнении с аналогичными по физическому принципу действия многослойными фильтрами Шольца.
Ключевые слова: управляемый оптический фильтр, управляемый оптический затвор, гофрированный волновод, запрещенные зоны фотонных кристаллов.
Abstract. A novel model of a tunable optical waveguide filter based on a corrugated planar waveguide made of electrooptic material is proposed. The principle of operation of the filter is based on а degenerate band gap manipulation. Degenerate band gaps form due to coupling of TE and TM modes of the waveguide under the application of the external electric field inducing the anisotropy of the waveguide material. Characteristics of а degenerate band gap are analyzed with the coupled mode method in approximation of the corrugation amplitude being small compared to the waveguide thickness. The anisotropy is also supposed to be weak. The proposed filter is much easier to fabricate than multilayer Šolc filters whose physical principles of operation are analogous.
Key words: tunable optical filter, tunable optical switch, corrugated waveguide, photonic crystal band gaps.
Введение.
Управляемые оптические интерференционные фильтры находят широкое применение в телекоммуникационных устройствах, например, мультиплексорах/демультиплексорах, модуляторах оптического сигнала.
Наиболее распространены фильтры Фабри-Перо. Управление спектром пропускания таких фильтров может осуществляться путем изменения размеров резонатора либо путем изменения характеристик заполняющего резонатор материала (например, с помощью электрооптического эффекта).
Другим типом интерференционных фильтров являются фильтры на основе фотонных кристаллов (ФК) и периодических волноводов (с периодически меняющимися вдоль оси волновода формой и размером сечения или свойствами материала волновода) [1]. Работа таких фильтров основана на наличии запрещенных зон (ЗЗ) в спектре ФК и периодических волноводов. Управление этими фильтрами также может осуществляться, например, путем изменения свойств материалов фильтра с помощью электрооптических эффектов [2]. При этом происходит сдвиг или изменение ширины ЗЗ.
Зонная структура периодического волновода, а значит и режим работы фильтра на его основе, зависит от поляризации волн. В случае управляемого фильтра на основе ФК зонная структура также различна для разных поляризаций электромагнитных волн, т.к. электрооптический эффект приводит к анизотропии диэлектрической проницаемости.
В данной статье будет рассмотрен оптический фильтр, работа которого не зависит от поляризации волн, работающий на частотах т.н. поляризационно вырожденных запрещенных зон [3]. Впервые поляризационно вырожденные ЗЗ были описаны в работах [4,5], где рассматривалась зонная структура одномерных ФК со слоями из одноосных материалов с периодически меняющейся от слоя к слою ориентацией оптических осей (в плоскости слоев). Такие ЗЗ являются общими для волн всех поляризаций. Опишем подробнее механизм формирования вырожденных ЗЗ на примере анизотропных ФК [5,3].
Рассмотрим ФК с периодом из двух слоев из одноосного материала. Ориентация оптических осей слоев меняется периодически от слоя к слою (в плоскости слоев) (см. рис. 1).

Рис. 1. Одномерный слоистый ФК со слоями из оптически одноосного материала. Жирными стрелками показаны ориентации оптических осей слоев (в плоскости слоев). Стрелка слева – волновой вектор падающей волны.
Пусть оптические оси всех слоев сонаправлены, тогда блоховские волны имеют фиксированную поляризацию (либо обыкновенную, либо необыкновенную). Каждая блоховская волна не чувствует анизотропии слоев ФК, т.к. уравнения Максвелла в этом случае могут быть разделены на две независимые части, каждая – для отдельной линейной поляризации. Вырожденная ЗЗ не возникает.
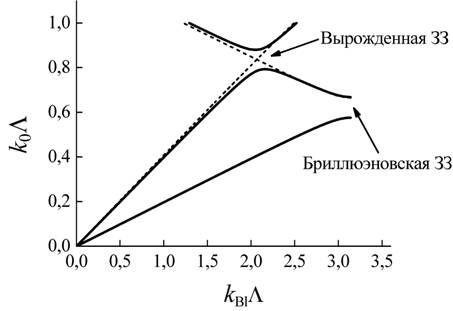
Рис. 2. Сплошные линии -
дисперсионные кривые анизотропного ФК с отклонением между ориентациями оптических
осей слоев, пунктирные – при сонаправленных оптических осях слоев. ![]() – волновое число в
вакууме,
– волновое число в
вакууме, ![]() –
блоховское волновое число,
–
блоховское волновое число, ![]() - период ФК.
- период ФК.
На рис. 2 пунктирные линии – дисперсионные кривые блоховских волн в этом случае.
Если отклонить оптические оси слоев друг от друга (в плоскости слоев), то при отражении и при прохождении через границы слоев обыкновенная волна будет частично рассеиваться в необыкновенную (и наоборот). Таким образом, в блоховской волне обыкновенная и необыкновенная компоненты оказываются гибридизованными. В этом случае дисперсионные кривые перезамыкаются и (см. сплошные кривые на рис. 2) на частотах вблизи пересечения пунктирных линий возникает вырожденная ЗЗ [3].
Частоты вырожденных ЗЗ соответствуют выполнению условия т.н. обменного брэгговского отражения [5]
где ![]() и
и ![]() – блоховские волновые числа,
соответствующие двум разным дисперсионным ветвям,
– блоховские волновые числа,
соответствующие двум разным дисперсионным ветвям, ![]() – период ФК,
– период ФК, ![]() – целое число. Качественно обменное
брэгговское отражение можно объяснить тем, что волна, проходящая через
элементарную ячейку и обратно, в одном направлении приобретает набег фаз,
соответствующий обыкновенному показателю преломления в слоях, а в другом
направлении – набег фаз, соответствующий необыкновенному показателю преломления
в слоях элементарной ячейки. Таким образом, появляется дополнительное условие
(1), при котором набег фаз волны, прошедшей через элементарную ячейку ФК и
обратно, может быть кратен
– целое число. Качественно обменное
брэгговское отражение можно объяснить тем, что волна, проходящая через
элементарную ячейку и обратно, в одном направлении приобретает набег фаз,
соответствующий обыкновенному показателю преломления в слоях, а в другом
направлении – набег фаз, соответствующий необыкновенному показателю преломления
в слоях элементарной ячейки. Таким образом, появляется дополнительное условие
(1), при котором набег фаз волны, прошедшей через элементарную ячейку ФК и
обратно, может быть кратен ![]() .
.
Как видно из рис. 2., вырожденная ЗЗ формируется не на границе, а внутри зоны Бриллюэна, причем одновременно для обеих дисперсионных ветвей, тогда как бриллюэновские ЗЗ (на границах зоны Бриллюэна) для разных дисперсионных ветвей в анизотропных ФК формируются на разных частотах. На частотах вырожденной ЗЗ действительные и мнимые части всех четырех блоховских волновых чисел равны с точностью до знака [3].
Оптические фильтры на основе ФК, работающие на частотах вырожденных ЗЗ, были предложены в [4,6]. Они представляют собой системы слоев из одноосных материалов с периодически меняющимися от слоя к слою ориентациями оптических осей (т.н. фильтры Шольца).
В [2] было предложено использовать электрооптический эффект для управления спектром пропускания многослойных фильтров Шольца. Однако, изготовление многослойных (для формирования же фильтров с четкой границей частотных диапазонов прозрачности и непрозрачности требуются структуры с десятками и сотнями слоев) структур из электрооптических материалов представляет большие трудности. Электрооптические слои нужно отжигать (для формирования кристаллической структуры), при этом свойства всех слоев заметно меняются, и сделать структуру с большим количеством слоев (50 и более) не представляется возможным.
В данной работе предлагается волноводный фильтр на основе гофрированного (периодически модулированного по толщине) планарного волновода из электрооптического материала. Принцип работы такого фильтра аналогичен принципу работы многослойного фильтра Шольца (непропускание волн на частотах вырожденной ЗЗ). Управляя внешним электрическим полем, можно открывать и закрывать вырожденную ЗЗ. Изготовление такого волновода требует напыления лишь одного слоя электрооптического материала с последующим нанесением гофра в виде борозд на одной из поверхностей, например, фокусированным ионным пучком.
На рис. 3. представлена схема описываемого гофрированного волновода. Для появления в спектре волновода вырожденной ЗЗ необходима связь (гибридизация) ТЕ- и ТМ-мод, распространяющихся в противоположных направлениях [1]. Данная связь осуществляется благодаря наведенной внешним электрическим полем анизотропии материала волновода (связь разных поляризаций, собственные моды анизотропного волновода уже не являются ТЕ- или ТМ-поляризованными) и гофру (связь волн с противоположным направлением распространения благодаря отражению от гофра).

Рис. 3. Схема рассматриваемого
планарного гофрированного волновода из анизотропного материала. Одна из главных
осей тензора ![]() направлена
вдоль оси
направлена
вдоль оси ![]() ,
две другие отклонены на некоторый угол от осей
,
две другие отклонены на некоторый угол от осей ![]() и
и ![]() . Волна в волноводе распространяется вдоль
оси
. Волна в волноводе распространяется вдоль
оси ![]() .
. ![]() – толщина волновода в
сечении, перпендикулярном оси
– толщина волновода в
сечении, перпендикулярном оси ![]() .
.
Постановка задачи.
Конфигурация
рассматриваемого нами волновода представлена на рис 3. Будем считать, что одна
из границ (нижняя) волновода плоская, а другая (верхняя) периодически
гофрирована, причем только в направлении оси ![]() , т.е. толщина
, т.е. толщина ![]() волновода периодически меняется
при движении вдоль оси
волновода периодически меняется
при движении вдоль оси ![]() , в направлении оси
, в направлении оси ![]() структура трансляционно
инвариантна. Для упрощения будем считать волновод погруженным в вакуум. Кроме
того, ограничимся рассмотрением распространения волн в волноводе вдоль оси
структура трансляционно
инвариантна. Для упрощения будем считать волновод погруженным в вакуум. Кроме
того, ограничимся рассмотрением распространения волн в волноводе вдоль оси ![]() (составляющая
(составляющая ![]() волнового вектора равна
нулю).
волнового вектора равна
нулю).
При включении электрического поля в результате электрооптического эффекта материал волновода становится анизотропным, ТЕ- и ТМ-моды гибридизуются и более не являются независимыми, как это было в отсутствие внешнего постоянного электрического поля. При расчетах пренебрежем потерями в материалах волновода.
Данная работа посвящена определению характеристик вырожденной ЗЗ для гофрированного волновода из анизотропного материала (частоты центра вырожденной ЗЗ, ее ширины и длины затухания волн в центре ЗЗ).
Применение метода связанных мод.
Для расчета характеристик вырожденной ЗЗ гофрированного волновода воспользуемся методом связанных мод. Описание данного метода можно найти, например, в [1], а также в [7], где он фигурирует под названием «метод поперечных сечений».
Рассмотрим сечение
гофрированного волновода плоскостью, параллельной координатной плоскости ![]() (см. рис. 3). Пусть
данное сечение пересекает ось
(см. рис. 3). Пусть
данное сечение пересекает ось ![]() в точке с координатой
в точке с координатой ![]() (т.е. сечение имеет координату
(т.е. сечение имеет координату ![]() ). Согласно методу
поперечных сечений [7] поля в данном сечении гофрированного волновода
представляются в виде линейной комбинации полей мод планарного (без гофра, с
постоянным сечением) волновода с таким же распределением материальных
параметров по сечению. Т.е. для каждого сечения гофрированного волновода
строится вспомогательный планарный волновод, вид которого (в нашем случае,
толщина
). Согласно методу
поперечных сечений [7] поля в данном сечении гофрированного волновода
представляются в виде линейной комбинации полей мод планарного (без гофра, с
постоянным сечением) волновода с таким же распределением материальных
параметров по сечению. Т.е. для каждого сечения гофрированного волновода
строится вспомогательный планарный волновод, вид которого (в нашем случае,
толщина ![]() )
зависит от координаты сечения
)
зависит от координаты сечения ![]() . В данные линейные комбинации входят, в
общем случае, как поля волноводных (т.е. распространяющихся вдоль плоскости
волновода и затухающих вне волновода) мод, так и поля излучательных (т.е.
распространяющихся в направлениях, перпендикулярных плоскости волновода
. В данные линейные комбинации входят, в
общем случае, как поля волноводных (т.е. распространяющихся вдоль плоскости
волновода и затухающих вне волновода) мод, так и поля излучательных (т.е.
распространяющихся в направлениях, перпендикулярных плоскости волновода ![]() , и затухающих вдоль
плоскости волновода) мод. Однако, как будет ясно в дальнейшем, только
ограниченный набор волноводных мод имеет существенное значение для расчета
характеристик вырожденной ЗЗ. Поэтому, для простоты, сразу ограничимся
линейными комбинациями лишь волноводных мод.
, и затухающих вдоль
плоскости волновода) мод. Однако, как будет ясно в дальнейшем, только
ограниченный набор волноводных мод имеет существенное значение для расчета
характеристик вырожденной ЗЗ. Поэтому, для простоты, сразу ограничимся
линейными комбинациями лишь волноводных мод.
Итак, поля в сечении с
координатой ![]() гофрированного
волновода представим в виде [7]:
гофрированного
волновода представим в виде [7]:
Здесь ![]() и
и ![]() - поля
- поля ![]() -й моды планарного волновода толщиной
-й моды планарного волновода толщиной ![]() в сечении
в сечении ![]() , их зависимость от
координаты сечения
, их зависимость от
координаты сечения ![]() более
сложная, чем просто экспоненциальная, т.к. толщина
более
сложная, чем просто экспоненциальная, т.к. толщина ![]() планарного волновода и его
положение вдоль оси
планарного волновода и его
положение вдоль оси ![]() также
определяется сечением
также
определяется сечением ![]() гофрированного
волновода. Будем рассматривать низкочастотный предел, когда существуют только
две волноводные моды планарного волновода с
гофрированного
волновода. Будем рассматривать низкочастотный предел, когда существуют только
две волноводные моды планарного волновода с ![]() (положительные
(положительные ![]() ) и две волноводные моды с
) и две волноводные моды с ![]() (отрицательные
(отрицательные ![]() ). Коэффициенты
). Коэффициенты ![]() в разложениях (2) меняются
от сечения к сечению и совпадают в разложениях электрического и магнитного
полей [7].
в разложениях (2) меняются
от сечения к сечению и совпадают в разложениях электрического и магнитного
полей [7].
Приведем выражения для волноводных
мод планарного волновода толщиной ![]() из анизотропного материала с тензором
диэлектрической проницаемости
из анизотропного материала с тензором
диэлектрической проницаемости
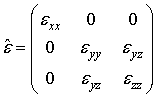 (3)
(3)
Вне волновода - вакуум. Данные
выражения могут быть найдены аналитически. Используемая система координат
изображена на рис. 3, т.е. плоскость волновода совпадает с плоскостью ![]() . Нас будут интересовать
только чётные моды, т.е. такие, составляющие
. Нас будут интересовать
только чётные моды, т.е. такие, составляющие ![]() электрического поля которых являются
четными функциями
электрического поля которых являются
четными функциями ![]() .
Такой выбор мод связан с тем, что в рассматриваемом нами низкочастотном пределе
волноводные моды являются четными. Будем считать, что нижняя граница планарного
волновода имеет координату
.
Такой выбор мод связан с тем, что в рассматриваемом нами низкочастотном пределе
волноводные моды являются четными. Будем считать, что нижняя граница планарного
волновода имеет координату ![]() , а верхняя
, а верхняя ![]() (в данном предположении, для удобства,
будут выписаны выражения для мод планарного анизотропного волновода, однако при
расчете характеристик вырожденной ЗЗ данная симметрия границ волновода
относительно
(в данном предположении, для удобства,
будут выписаны выражения для мод планарного анизотропного волновода, однако при
расчете характеристик вырожденной ЗЗ данная симметрия границ волновода
относительно ![]() будет
в общем случае отсутствовать). В случае
будет
в общем случае отсутствовать). В случае ![]() волноводные (незатухающие в направлении
волноводные (незатухающие в направлении ![]() и затухающие в
направлении
и затухающие в
направлении ![]() )
моды имеют вид:
)
моды имеют вид:
 при
при
![]() , (4а)
, (4а)
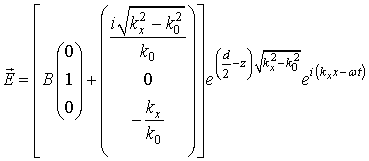 при
при
![]() , (4б)
, (4б)
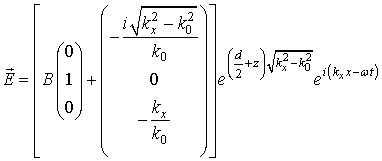 при
при
![]() . (4в)
. (4в)
Здесь ![]() – волновое число в вакууме,
– волновое число в вакууме,
 ,
,
 ,
, ![]() ,
,
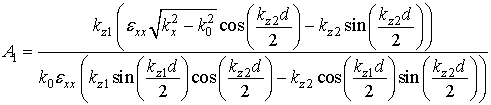 ,
,
 ,
,
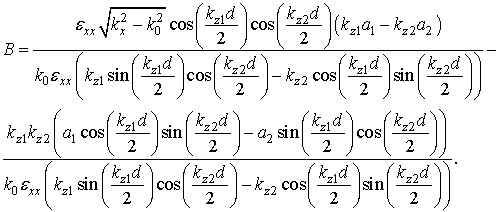
![]() ,
, ![]() и
и ![]() удовлетворяют системе уравнений:
удовлетворяют системе уравнений:
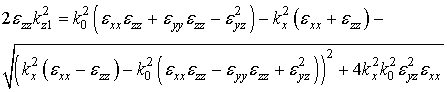 , (5а)
, (5а)
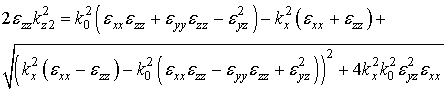 , (5б)
, (5б)
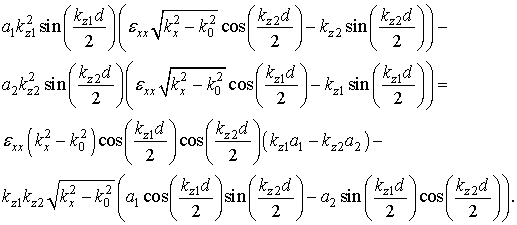 (5в)
(5в)
Величины ![]() и
и ![]() определяются уравнениями (5) с точностью
до знака, поэтому без ограничений общности будем считать, что
определяются уравнениями (5) с точностью
до знака, поэтому без ограничений общности будем считать, что ![]() и
и ![]() .
.
Соответствующие магнитные поля имеют вид:
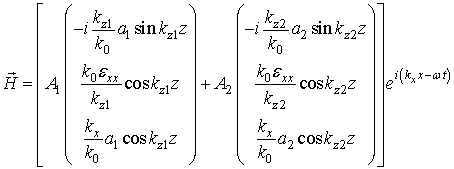 при
при
![]() , (6а)
, (6а)
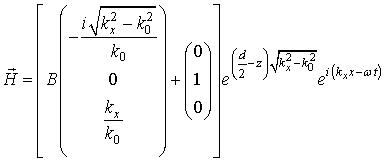 при
при
![]() , (6б)
, (6б)
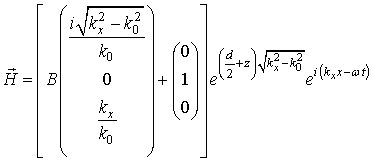 при
при
![]() . (6в)
. (6в)
Оставшаяся часть данного раздела статьи посвящена
нахождению и решению уравнений для коэффициентов ![]() .
.
Поля (2) в гофрированном волноводе удовлетворяют уравнениям Максвелла:
![]() ,
, ![]() , (7)
, (7)
где
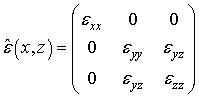 при
при ![]() ,
,
![]() при
при
![]() и
и ![]() . В качестве
. В качестве ![]() выберем некоторую
среднюю толщину волновода, например,
выберем некоторую
среднюю толщину волновода, например, 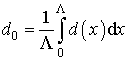 , где
, где ![]() - период гофра.
- период гофра.
Подстановка (2) в (7) дает
 , (8а)
, (8а)
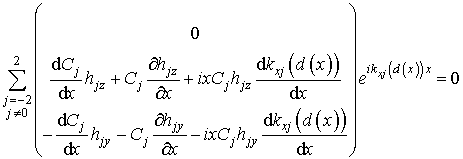 (8б)
(8б)
Уравнение (8а) скалярно умножим на ![]() , уравнение (8б) – на
, уравнение (8б) – на ![]() , затем сложим их и
проинтегрируем по
, затем сложим их и
проинтегрируем по ![]() ,
,
![]() .
.
При этом воспользуемся соотношением ортогональности мод планарного волновода:
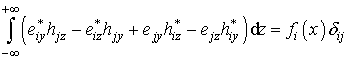 , где
, где ![]() - символ Кронекера.
- символ Кронекера.
![]() периодически зависит от
периодически зависит от ![]() с периодом гофра. В
итоге получим уравнения для
с периодом гофра. В
итоге получим уравнения для ![]() :
:
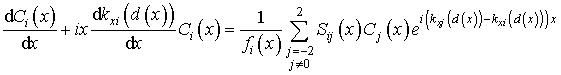 . (9)
. (9)
Здесь коэффициенты связи мод имеют вид
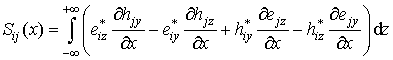 (10)
(10)
Напомним, что все входящие в (10)
поля зависят от ![]() периодически
с периодом гофра. После замены переменных
периодически
с периодом гофра. После замены переменных
![]() ,
,
![]() ,
,
где ![]() -
- ![]() -я составляющая волнового вектора
-я составляющая волнового вектора ![]() -й моды планарного
волновода со средней толщиной
-й моды планарного
волновода со средней толщиной ![]() , уравнения (9) преобразуются к виду
, уравнения (9) преобразуются к виду
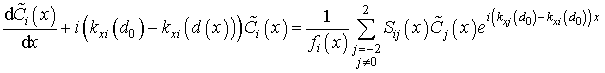 (11)
(11)
Функции ![]() и
и 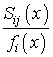 являются периодическими с периодом гофра,
поэтому можно разложить их в ряд Фурье. В этом случае (11) перейдет в:
являются периодическими с периодом гофра,
поэтому можно разложить их в ряд Фурье. В этом случае (11) перейдет в:
![]() ,
, ![]() - параметр обратной решетки,
- параметр обратной решетки, ![]() и
и 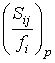 , соответственно, - коэффициенты
Фурье функций
, соответственно, - коэффициенты
Фурье функций ![]() и
и
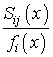 . Полученная
система (12) может быть значительно упрощена в предположении малой по сравнению
с толщиной волновода амплитуды гофра и малой анизотропии материала волновода. В
этом случае связь мод разных поляризаций и разных направлений распространения
мала, малы в сравнении с
. Полученная
система (12) может быть значительно упрощена в предположении малой по сравнению
с толщиной волновода амплитуды гофра и малой анизотропии материала волновода. В
этом случае связь мод разных поляризаций и разных направлений распространения
мала, малы в сравнении с ![]() коэффициенты при
коэффициенты при ![]() в (12) и, следовательно, функции
в (12) и, следовательно, функции
![]() меняются
слабо на расстояниях порядка длины волны в волноводе. Поэтому в системе
уравнений (12) можно оставить только те слагаемые, у которых фаза множителей
при
меняются
слабо на расстояниях порядка длины волны в волноводе. Поэтому в системе
уравнений (12) можно оставить только те слагаемые, у которых фаза множителей
при ![]() меняется
медленно.
меняется
медленно.
Нас в первую очередь интересуют характеристики вырожденных запрещенных зон. Ограничившись частотами в окрестности вырожденной ЗЗ, например, при выполнении условия
сведем (12) к системе
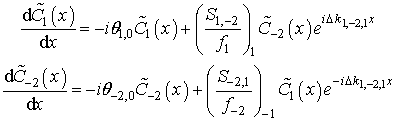 (14)
(14)
Условие (13) является аналогом условия (1) обменного брэгговского отражения.
Видно, что система (14) связывает
амплитуды ![]() и
и ![]() волн с противоположным
направлением распространения (разные знаки индексов) и с разной поляризацией
(разные модули индексов). Это отражает необходимую для формирования вырожденной
ЗЗ гибридизацию волн противоположных направлений и разных поляризаций.
волн с противоположным
направлением распространения (разные знаки индексов) и с разной поляризацией
(разные модули индексов). Это отражает необходимую для формирования вырожденной
ЗЗ гибридизацию волн противоположных направлений и разных поляризаций.
Возможность отбросить в
уравнениях системы (12) все слагаемые с быстро меняющейся фазой множителей при ![]() обосновывает также то,
что в разложениях (2) не были учтены излучательные моды.
обосновывает также то,
что в разложениях (2) не были учтены излучательные моды.
Система (14) может быть сведена к линейной системе с постоянными коэффициентами с помощью замены
![]() ,
,
![]() .
.
После замены из (14) получим
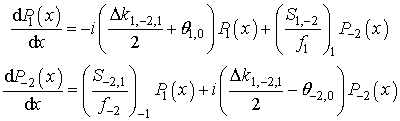 . (15)
. (15)
В области частот, в
которой собственные значения матрицы системы (15) обладают ненулевой
действительной частью, наблюдается экспоненциальный рост или затухание модуля
амплитуд ![]() и
и ![]() и, следовательно,
и, следовательно, ![]() и
и ![]() , т.е. запрещенная зона.
, т.е. запрещенная зона.
Xарактеристики вырожденных запрещенных зон.
С помощью полученных уравнений
связанных мод (15) рассчитаны характеристики вырожденной запрещенной зоны
волновода. Были взяты следующие параметры волновода: тензор диэлектрической
проницаемости материала волновода
 , уравнение гофрированной поверхности
волновода
, уравнение гофрированной поверхности
волновода ![]() ,
притом что нижняя граница соответствует координате
,
притом что нижняя граница соответствует координате ![]() . На рис. 4 представлен график зависимости
мнимой части блоховского волнового вектора (для обеих дисперсионных ветвей эти
величины равны по модулю на частотах вырожденной ЗЗ) от частоты
. На рис. 4 представлен график зависимости
мнимой части блоховского волнового вектора (для обеих дисперсионных ветвей эти
величины равны по модулю на частотах вырожденной ЗЗ) от частоты ![]() в окрестности
вырожденной запрещенной зоны.
в окрестности
вырожденной запрещенной зоны.
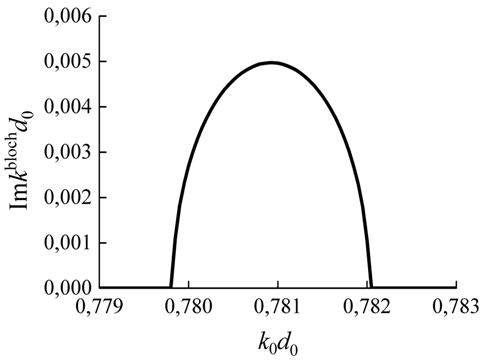
Рис. 4. Зависимость мнимой части блоховского волнового числа (обратного масштаба затухания волны по мере прохождения в волновод) от частоты в окрестности вырожденной запрещенной зоны.
Итак, из рис. 4 видно,
что в окрестности частоты ![]() мнимая часть блоховского волнового вектора
не равна нулю, т.е. имеется запрещенная зона, причем общая для обеих
дисперсионных ветвей. Частота центра ЗЗ удовлетворяет условию (13) брэгговского
отражения. Действительно, для вышеприведенных параметров волновода
мнимая часть блоховского волнового вектора
не равна нулю, т.е. имеется запрещенная зона, причем общая для обеих
дисперсионных ветвей. Частота центра ЗЗ удовлетворяет условию (13) брэгговского
отражения. Действительно, для вышеприведенных параметров волновода ![]() на частоте
на частоте ![]() .
.
Сдвиг между частотой центра вырожденной ЗЗ и частотой, даваемой условием (13), стремится к нулю с уменьшением анизотропии материала и амплитуды гофра волновода.
Исходя их рисунка 4, можно
заключить, что в центре запрещенной зоны волна затухает в ![]() раз на длине в 80 периодов
волновода.
раз на длине в 80 периодов
волновода.
Заключение.
Предложен управляемый
внешним электрическим полем оптический фильтр на основе планарного
гофрированного волновода из электрооптического материала. Работа данного
фильтра основана на управлении вырожденной запрещенной зоной, возникающей в
результате связи ТЕ и ТМ мод благодаря наведенной внешним полем анизотропии
материала волновода. В статье рассчитаны характеристики вырожденной запрещенной
зоны волновода с помощью теории связанных мод в приближении малой по сравнению
с толщиной волновода амплитуды гофра и малой анизотропии материала волновода.
Преимуществом предложенной конструкции фильтра является простота изготовления в
сравнении с аналогичными по физическому принципу действия многослойными
фильтрами Шольца. Предложенный волноводный фильтр может быть использован в
качестве управляемого затвора, интегрируемого в оптический волновод. Оценка
времени установления решения в волноводе, на длине которого волна затухает в 10
раз (200 периодов волновода), после изменения параметров материала под
действием внешнего поля дает ![]() с (время 10-ти проходов по волноводу волны
с частотой зеленого света). Поэтому время переключения фильтра между режимами «прозрачности»
и «непрозрачности» определяется временем изменения тензора диэлектрической
проницаемости под действием электрооптического эффекта и имеет порядок
с (время 10-ти проходов по волноводу волны
с частотой зеленого света). Поэтому время переключения фильтра между режимами «прозрачности»
и «непрозрачности» определяется временем изменения тензора диэлектрической
проницаемости под действием электрооптического эффекта и имеет порядок ![]() с.
с.
Литература.
1. А. Ярив, П. Юх. Оптические волны в кристаллах. М.: Мир, 1987.
2. G. Shabtay, E. Eidinger, Z. Zalevsky, “Tunable birefringent filters – optimal iterative design,” Optics Express 10, 1534-1541 (2002).
3. A.M. Merzlikin, M. Levy, A.A. Jalali and A.P. Vinogradov, “Polarization degeneracy at Bragg reflectance in magnetized photonic crystals,” Phys. Rev. B. 79, 195103 (2009).
4. I. Šolc, “A new kind of double refracting filter,” Czech. J. Phys., Sect. A 4, 65-66 (1954).
5. P. Yeh. “Electromagnetic propagation in birefringent layered media,” J. Opt. Soc. Am. 69, 742-756 (1979).
6. I. Šolc, “Birefringent chain filters,” J. Opt. Soc. Am. 55, 621-625 (1965).
7. Б.З. Каценеленбаум. Теория нерегулярных волноводов с медленно меняющимися параметрами. М.: Изд. академии наук СССР. 1961.
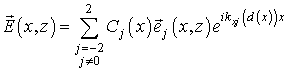 ,
,
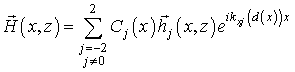 (2)
(2)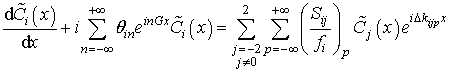 , (12)
, (12)