Однополосковая металлодиэлектрическая меандровая линия
В. А. Калошин, В. И. Калиничев
Институт радиотехники и электроники им. В.А.Котельникова РАН
Получена 14 сентября 2011 г.
Аннотация. Предложен новый тип однопроводниковых линий - однополосковая металлодиэлектрическая меандровая линия. Методом конечных элементов проведено исследование дисперсионных характеристик линии в частном случае геометрии меандра (в виде сопряженных полуокружностей). Показано, что новая линия имеет малые потери и большое относительное замедление.
Ключевые слова: линии поверхностной волны, однопроводниковые линии.
Abstract. A new type of lines - Single – Strip Meander Metal - Dielectric Line have been proposed. In a particular case of meander geometry (conjugate semicircles) the dispersion characteristics of the line have been investigated using Finite Element Method. It is shown that the new line has small losses and large relative slowing.
Keywords: surface wave lines, single-conductor lines.
Введение
Однополосковая линия (ОПЛ), представляющая собой металлический полосок на диэлектрическом слое (рис.1а), была предложена в [1] в качестве альтернативы микрополосковым линиям. Строгое электродинамическое обоснование существования поверхностной волны в этой линии приведено в работе [2]. Экспериментальное подтверждение существования этой моды и измерение погонных потерь проведено в работе [3]. Недостатком ОПЛ является небольшое относительное замедление, из-за чего ограничены возможности получения малых потерь в элементах на основе этой линии [4-9].
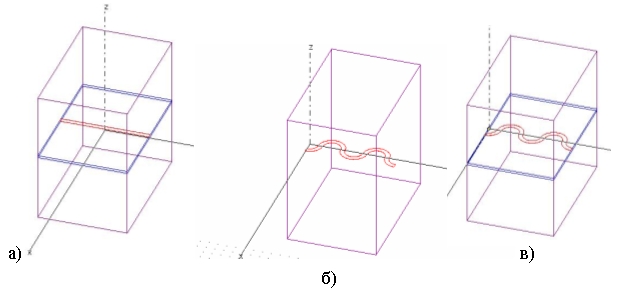
Рис.1. Исследуемые линии в закрытом резонаторе
а) ОПЛ, б) ОМЛ, в) ОММЛ.
Однополосковая меандровая линия (ОМЛ), представляющая собой металлический полосок в форме меандра (рис.1б), предложена в [10]. На основе этой линии удалось реализовать элементы с малыми потерями [11]. К сожалению ОМЛ не технологична и, кроме того, возникает проблема ее крепления, поскольку она является открытой линией. Использование плотных диэлектриков в качестве подложки в интегральных схемах на основе ОМЛ приводит к увеличению потерь. Использование вспененных диэлектриков – к технологическим трудностям.
В данной работе предлагается однополосковая металлодиэлектрическая меандровая линия (ОММЛ), металлический полосок которой имеет форму меандра и нанесен на диэлектрическую пленку (рис. 1в). При использовании такой линии в интегральных схемах в качестве подложки можно использовать вспененные диэлектрики. Как будет показано ниже, основная мода ОММЛ в отличие от ОПЛ обладает большим относительным замедлением, что приводит к быстрому спаданию амплитуды поля при удалении от полоска. Это свойство моды ОММЛ позволит в перспективе использовать ее как базовую линию для построения элементов интегральных схем с малыми потерями, а при использовании ее в качестве гибкого тракта позволяет крепить за края диэлектрической пленки.
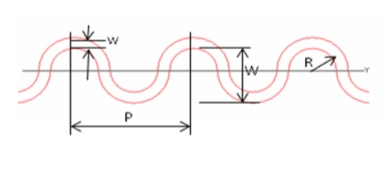
Рис.2. Геометрия меандра.
Параметры исследуемых ОМЛ и ОММЛ с меандром в форме одинаковых сопрягающихся полуокружностей (см. рис.3): радиус R=2.5 мм, период P=10 мм; ширина полоска w=1 мм, толщина полоска -18 мкм, материал – медь (σ=5.8х107 1/ом). Параметры подложки для ОММЛ: относительная диэлектрическая проницаемость ε=2.55, для ОПЛ - ε=2.55 и ε=13, толщина подложки для обеих линий h=0.5 мм, tgδ=0.001.
1. Сравнение ОМЛ и ОММЛ
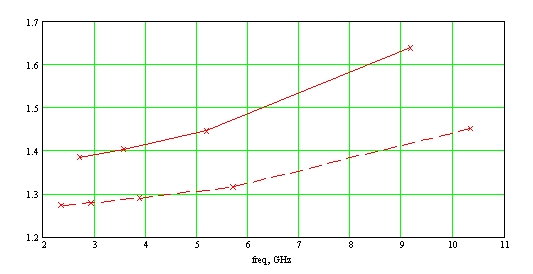
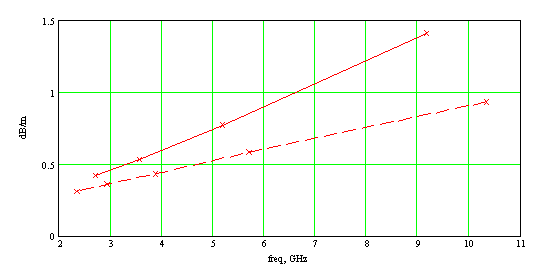
Результаты расчета дисперсионных характеристик коэффициента замедления и погонного затухания основной моды ОМЛ и ОММЛ приведены на рис.3а и 3б, соответственно.
а)
б)
Рис.3. Зависимость коэффициента замедления (а) и погонных потерь (б) поверхностной волны от частоты в форме сопрягающихся одинаковых полуокружностей: сплошная линия – ОММЛ, пунктир – ОМЛ.
Как видно из рисунков и как следовало ожидать, для одинаковых параметров меандра ОММЛ имеет большее замедление и затухание в сравнении с ОМЛ.
Распределение амплитуды электрического поля основной моды ОММЛ и использованная для расчета сетка показаны на рис.3.
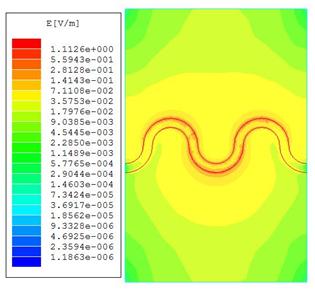
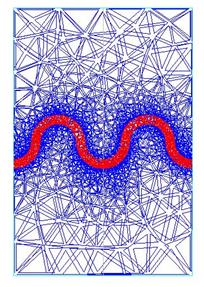
(а) (б)
Рис. 3. (а) - Распределение амплитуды электрического поля (логарифмический масштаб) в плоскости меандра на резонансной частоте основного типа колебаний в резонаторе длиной 20 мм, (б) - соответствующая сетка в методе конечных элементов.
Как видно из рисунка, максимальная напряженность и скорость изменения поля Е в плоскости меандра имеет место вблизи краев полоски (красный цвет в цветовой шкале на рис. 3а). Этой области соответствует наиболее плотная сетка в расчете методом конечных элементов (рис. 3 б).
Скорость спадания напряженности поля в подложке при удалении от оси меандра показана на рис. 4. Значение Х=15 мм соответствует оси меандра, Х=0 - положению дальней стенки резонатора на рис. 1б, Х=30 мм – положению ближней стенки резонатора на том же рис. Пики в распределении в плоскости меандра соответствуют краям полоски в точках ее пересечения с осью Х. Поле на данной резонансной частоте спадает в е раз на расстоянии 8.8 мм от оси линии (5.8 мм от внешнего края полоски).
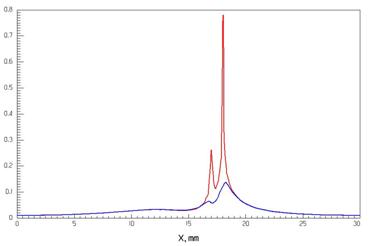
Рис. 4. Распределение магнитуды электрического поля вдоль поперечной координаты Х в центральной плоскости резонатора на резонансной частоте основного типа колебаний: красный цвет – на верхней стороне подложки в плоскости меандра, синий цвет – на нижней стороне подложки.
2. Сравнение ОММЛ и ОПЛ
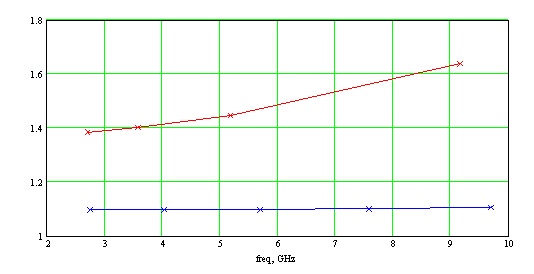
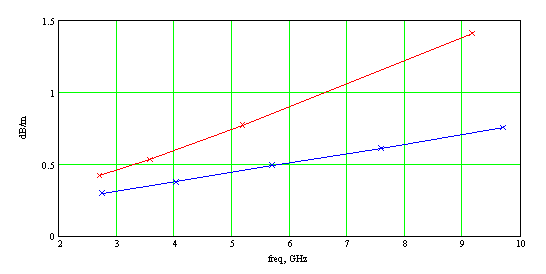
Сначала рассмотрим вариант, в котором ОПЛ имеет те же параметры подложки ε=2.55, h=0.5 мм, что и ОММЛ. Результаты расчета дисперсионных характеристик коэффициента замедления и погонного затухания основной моды ОПЛ и ОММЛ приведены на рис.5а и 5б, соответственно.
(а)
(б)
Рис. 5. Коэффициент замедления (а) и погонное затухание (б) в диапазоне частот:
красный цвет – ОММЛ, синий цвет – ОПЛ.
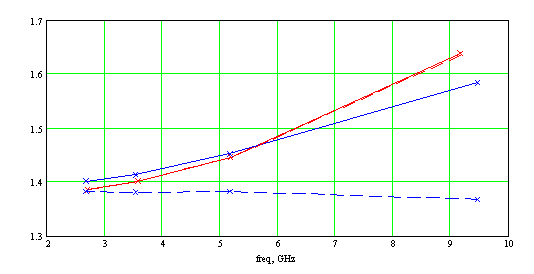
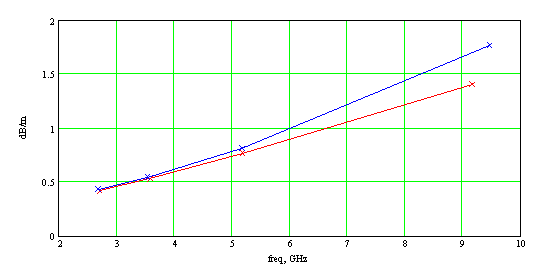
На подложке ε=2.55 затухание ОПЛ меньше, чем у меандра на той же подложке. Однако это уменьшение затухания достигается за счет значительно меньшего замедления ОПЛ и, вследствие этого, меньшей связи волны с линией. Такая линия практически непригодна в качестве базовой линии для интегральных схем. Увеличение замедления ОПЛ можно обеспечить различными путями, например, увеличить проницаемость подложки при той же ее толщине. Выберем параметры подложки ОПЛ: ε=13, толщина 0.5 мм, tgδ=0.001. Результаты расчета дисперсионных характеристик коэффициента замедления и погонного затухания основной моды ОПЛ и ОММЛ приведены на рис.3а и 3б, соответственно. Параметры подложки ОММЛ те же, что и ранее: ε=2.55, толщина 0.5 мм, tgδ=0.001.
(а)
(б)
Рис. 6. Замедление (а) и погонное затухание (б) в диапазоне частот:
красный цвет – меандр на подложке ε=2.55, синий цвет – ОПЛ на подложке ε=13. Пунктир – относительное замедление (замедление относительно Н-моды подложки).
Отметим, что коэффициенты замедления ОММЛ, расположенной на подложке с ε = 2.55 и ОПЛ, расположенной на подложке с ε = 13, близки. В низкочастотной области несколько больше замедление в ОПЛ, в высокочастотной области – наоборот. При этом затухание меандра меньше затухания ОПЛ во всем исследованном диапазоне частот. Разница в затухании ОММЛ и ОПЛ растет с ростом частоты. Относительное замедление основной моды ОММЛ больше, чем ОПЛ, причем разница также растет с ростом частоты.
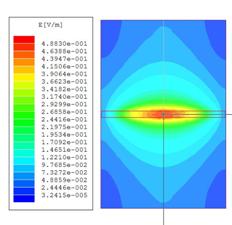

(а) (б)
Рис. 7. (а) - Распределение магнитуды электрического поля (линейный масштаб) в плоскости ОПЛ в резонаторе длиной 20 мм на резонансной частоте основного типа колебаний, (б) - соответствующая ему сетка в методе конечных элементов.
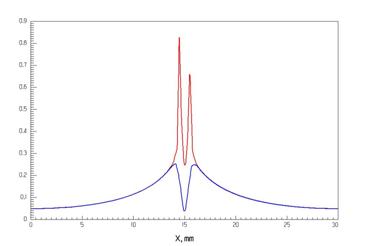
Рис. 8. Распределение магнитуды электрического поля вдоль поперечной координаты Х в центральной плоскости резонатора на резонансной частоте основного типа колебаний: красный цвет – на верхней стороне подложки в плоскости ОПЛ, синий цвет – на нижней стороне подложки.
Значение Х=15 мм соответствует оси линии, Х=0 и Х=30 мм - положению стенок резонатора на рис. 1с. Пики в распределении в плоскости ОПЛ соответствуют краям полоски. Поле на данной резонансной частоте спадает в е раз на расстоянии 9.2 мм от оси линии (8.7 мм от внешнего края полоски).
Заключение
Как показано выше, абсолютное замедление основной моды новой линии (ОММЛ) не только больше, чем замедление линий-прототипов (ОПЛ и ОМЛ), но и больше их суммарного замедления. При этом относительное замедление в ОММЛ также больше, чем в ОПЛ. Новая линия имеет меньшие погонные потери при таком же коэффициенте замедления, чем ОПЛ. Дальнейшего снижения погонного затухания при незначительном снижении замедления можно добиться, например, путем увеличения ширины проводника ОММЛ, а также изменением других параметров меандра.
Таким образом, печатный меандр на тонкой диэлектрической подложке с небольшим значением диэлектрической проницаемости имеет лучшие электродинамические характеристики по сравнению с ОПЛ с близким замедлением (на подложке с повышенным значением проницаемости). С другой стороны, ОММЛ имеет технологические преимущества при реализации в качестве линии передачи и базовой линии для интегральных схем по сравнению с ОМЛ.
Работа выполнена при поддержке РФФИ, проект №10-07-00709-а.
Литература
1. В.В. Шевченко, Микрополосковый волновод: Авт. свид. СССР SU № 1626282 А1 // Б.И. 1991. №5. С. 150
2. Темнов В.М. // Изв. Высш. Уч. Зав. Радиофизика. 1991. Т.34. № 3. С. 286.
3. В.Л.Бирюков, В.И.Калиничев, В.А.Калошин, Е.А.Скородумова, Исследование дисперсионных характеристик полосковых линий передачи в сантиметровом и миллиметровом диапазонах волн , РиЭ, 2009 Т. 54. №10. С. 1226
4. Грачёв Г.Г., Калиничев В.И., Шевченко В.В. Изгиб и излом микрополоскового волновода, РиЭ, 2006, Т. 51, №8, С. 916
5. Грачёв Г.Г., Шевченко В.В. Микрополосковые волноводные переходы. РиЭ, 2007, Т.52, №6. С. 687.
6. В.И.Калиничев, В.А.Калошин, Е.А.Скородумова, Возбуждение однополосковой линии микрополосковой и коаксиальной линиями, ЖРЭ, 2009, №1
7. В.И.Калиничев, В.А.Калошин, Е.А.Скородумова, Возбуждение однополосковой линии прямоугольным металлическим волноводом, ЖРЭ, 2009, №1
8. Грачёв Г.Г., Калиничев В.И., Калошин В.А., Скородумова Е.А. Исследование характеристик излучателя на однополосковой линии. ЖРЭ, 2010, №1.
9. Грачёв Г.Г., Калиничев В.И., Калошин В.А.,Исследование делителей мощности на основе однополосковой линии, ЖРЭ, 2010, №1.
10. Арсеньева Е.М, В.И.Калиничев, В.А.Калошин, Новые типы линий для радиосвязи в УКВ и СВЧ диапазонах, Труды III Всероссийской конференции, Радиолокация и радиосвязь, М., ноябрь, 2009.
11. Грачёв Г.Г., Калошин В.А., Исследование двух способов возбуждения меандровых линий, ЖРЭ, 2011, №3.