УДК 537.874
ОПИСАНИЕ ПЛАЗМОННОГО РЕЗОНАТОРА СО СЛОЕМ ДВУМЕРНОГО ЭЛЕКТРОННОГО ГАЗА В ТЕРМИНАХ СОСРЕДОТОЧЕННЫХ ПАРАМЕТРОВ
В. Л. Семененко, Ю. В. Стебунов, В. Г. Лейман, А. В. Арсенин
Московский физико-технический институт (государственный университет), Лаборатория нанооптики и фемтосекундной электроники
Получена 8 сентября 2012 г.
Аннотация. Представлено описание плазмонного резонатора со слоем двумерного электронного газом в терминах сосредоточенных параметров и определены условия возбуждения терагерцевых колебаний в слое двумерного электронного газа.
Ключевые слова: плазмонный резонатор, двумерный электронный газ, терагерцевое излучение.
Abstract. Description of the plasmon resonator with the two dimensional electron gas layer is presented in terms of lumped parameters. The conditions of excitation terahertz oscillations in the two dimensional electron gas layer are found.
Keywords: plasmon resonator, two-dimensional electron gas, terahertz radiation.
Точный расчет сосредоточенных параметров плазмонных резонаторов представляет собой достаточно трудоемкую процедуру. Однако, по результатам ее выполнения, как было показано в работах [1, 2], уравнения для сосредоточенных параметров всегда сводятся к одному и тому же виду, в большинстве случаев ‑ к линейному уравнению второго порядка. Коэффициенты в таких уравнениях с точностью до постоянного множителя ~ 1 можно выбрать из общих соображений. Так, для полуволнового оптического плазмонного резонатора можно записать следующее уравнение:
(1)
где 
‑
величина нормальной (к металлическому слою) компоненты амплитуды колебаний
электрического поля оптической плазмонной волны в слое металла с ограниченной
длиной (равной половине длины волны плазмона) на краю слоя, 
‑
частота столкновений электронов в модели диэлектрической проницаемости Друде, 
‑
собственная частота оптического резонатора, 
‑ коэффициент
усиления поля за счет плазмонного резонанса, и 
‑ коэффициент
прохождения поля падающей волны лазерного излучения 
в призму в
схеме Кретчмана [3] при нормальном падении, диэлектрическая проницаемость
материала призмы взята равной 
.
Теперь
перейдем к описанию терагерцевого резонатора в терминах сосредоточенных
параметров. Пусть на его длине равной 
будет укладываться одна длина
волны терагерцевого плазмона. Данная стоячая волна терагерцевой частоты может
быть возбуждена при наличии постоянного напряжения 
между металлом и слоем
двумерного электронного газа при модуляции значения диэлектрической константы
нелинейного материала между ними в поле оптического плазмона. Пусть длина
оптического резонатора равна длине терагерцевого, тогда распределение
нормальной компоненты электрического поля в ней (внутри нелинейного диэлектрика
между
металлом и двумерным электронным газом) будет:
(2)
При этом диэлектрическая проницаемость зависит квадратично от приложенного поля:
(3)
Пренебрегая х-компонентой поля и
усредняя по высокой оптической частоте,
получим:
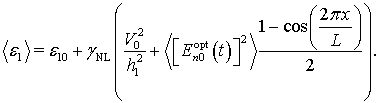(4)
Далее, имея ввиду статическое соотношение
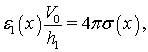(5)
где 
‑
распределенная электронная плотность в двумерном электронном газе, можно
записать для динамического случая:
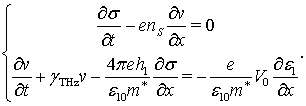(6)
Перейдя к Фурье компонентам по времени в данной системе и подставив в нее выражение (4), а также в качестве неизвестных функций
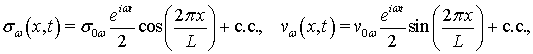(7)
для
комплексной амплитуды 
получим следующее выражение:
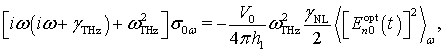(8)
где 
‑
собственная частота плазменных колебаний в двумерном электронном газе,
определяемая соотношением:
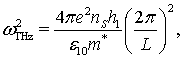(9)
‑
Фурье-компонента функции от времени 
:
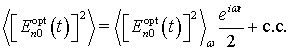(10)
Соотношение (8) соответствует следующему динамическому уравнению:
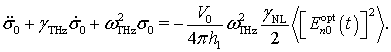(11)
Далее,
сделав для однородной записи переобозначение 
, запишем последнее уравнение
совместно с уравнением (1):
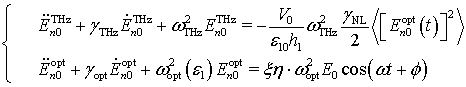(12)
С учетом поля терагерцевого плазмона, величина нелинейной диэлектрической проницаемости запишется следующим образом:
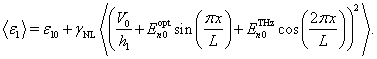(13)
Предполагая,
что меняется
слабо, оставим лишь линейную по полю 
добавку:
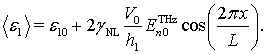(14)
Теперь, чтобы выяснить, как влияет такое изменение диэлектрической проницаемости в нелинейном слое на величину собственной частоты оптического резонатора, рассмотрим следующую задачу решения линейного дифференциального уравнения с граничными условиями:
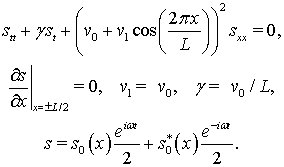(15)
В
случае если бы не было модуляции фазовой скорости волны, т.е. 
,
решение и соответствующее резонансное условие были бы следующими:
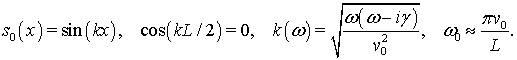(16)
При наличии слабого возмущения, резонансное условие становится следующим:
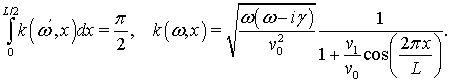(17)
Из
последних выражений видно, что смещенная резонансная частота 
имеет
относительно невозмущенного значения 
добавку, квадратичную по величине
возмущения:
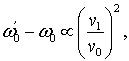(18)
что существенно понижает возможности генерации в данной схеме.
Однако, как было показано в работе [4], собственные и резонансные профили плазменных колебаний в плазменных резонаторах ограниченной длины сильно отличаются от гармонических. Таким образом, в выражении (2) при более детальном рассмотрении должен стоять не «синус», а какая-то более сложная нечетная функция. Точно также, в выражении для профилей вынужденных колебаний в двумерном электронном газе (7) должны на самом деле быть не «косинусы» и «синусы», а тоже более сложные зависимости, причем отличные от тех, что фигурировали бы в случае металлического резонатора оптических плазмонов. Вышесказанное заставляет принять то положение, что в рассматриваемом случае связанных оптического и терагерцевого резонаторов, смещение собственной частоты оптических колебаний должно быть пропорционально первой степени амплитуды малого изменения фазовой скорости:
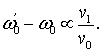(19)
Оценку
коэффициента пропорциональности произведем из следующих соображений: заменим в
выражении (17) для сдвинутой частоты 
функцию пространственного изменения
фазовой скорости 
на 
, где 
‑
поправочный множитель. В результате получим:
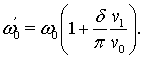(20)
Теперь, используя расчеты оптических плазменных волн в многослойных системах, приняв толщину серебряного металлического слоя равной 40 нм, слоя GaAs ‑ 20 нм и слоя AlGaAs ‑10 нм. При этом в качестве диэлектрической функции серебра была взята функция из модели Друде
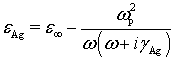(21)
при
параметрах: 
, 
и 
.
диэлектрические проницаемости и 
материалов GaAs и 
взяты при 
с
использованием эмпирической формулы для показателя преломления соединения :
(22)
При
малом изменении фазовая скорость плазменных волн
изменяется следующим образом:
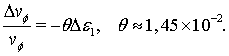(23)
Теперь мы можем выписать связанную систему уравнений для сосредоточенных параметров, описывающих колебания в оптическом и терагерцевом резонаторах:
(24)
Сделаем для удобства следующие обозначения:
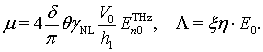(25)
Далее,
решим второе уравнение системы при постоянном значении :
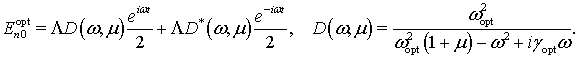(26)
Усредненное
значение 
, фигурирующее в первом уравнении
получается следующим:
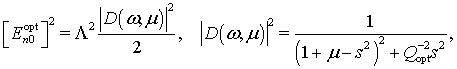(27)
где 
и
.
В дальнейшем нас будет интересовать максимальное значение производной
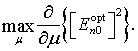(28)
Очевидно,
что подстраивая значение 
, можно добиться максимума данной
производной, причем как одного, так и другого знака. Поэтому для удобства можно
положить 
, вычислить максимальное значение
производной, а потом считать, что она может быть таковой и при 
,
т.к. значение параметра не является фиксированным. Итак,
надо решить уравнение:
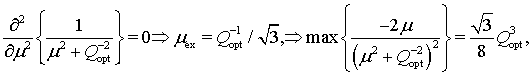(29)
или
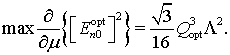(30)
Подставляя
в уравнение для колебаний терагерцевого резонатора выражение (27), в котором
функция 
запаздывает
на время релаксации оптического резонатора 
, получим уравнение
свободных терагерцевых колебаний с модифицированным декрементом:
(31)
Условие
когда 
соответствует
возникновению параметрической неустойчивости в системе. Это произойдет при
превышении интенсивности падающего из вакуума на систему излучения 
:
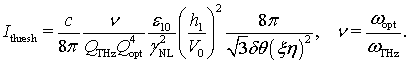(32)
Расчет пороговой
интенсивности поля по данной формуле дает следующие значения: 
,
или при пороговой амплитуде поля в падающей волне, равной 
.
Полученные величины пороговой интенсивности поля для параметрической генерации плазменных волн терагерцевой частоты достаточно велики. для практической реализации в гибридных схемах с оптическим и плазменным резонаторо. Тем не менее, продемонстрирована возможность параметрической генерации плазменных волн терагерцевой частоты, которая при должном подборе материалов с их параметрами может обеспечить гораздо более низкие пороги генерации. Так, использование в качестве нелинейного диэлектрика InSb и инфракрасного лазера в качестве опорной моды может уменьшить пороговую амплитуду падающей волны на 3 и более порядков [5] в силу сильных нелинейных свойств данного материала.
Работа выполнена при частичной финансовой поддержке Министерства образования и науки Российской Федерации в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы» (контракт № 07.514.11.4086).
1. Braginsky V.B., Manukin A. B. Measurement of Weak Forces in Physics Experiments (Chicago: University of Chicago Press. 1977).
2. Арсенин А.В., Гладун А.Д., Лейман В.Г., Семененко В.Л., Рыжий В.И. Параметрическая неустойчивость в наноэлектромеханическом детекторе модулированного излучения терагерцевого диапазона на основе транзистора с высокой подвижностью электронов и подвижным упругим затвором // Радиотехника и электроника. 2009. Т. 54. № 11. C. 1394 - 1402.
3. Kretschmann E., Raether H. Radiative decay of non radiative plasmons excited by light // Z. Naturforsch. 1968. Vol. A23. P. 2135.
4. Арсенин А.В., Гладун А.Д., Лейман В.Г., Семененко В.Л., Рыжий В.И. Плазменные колебания двумерного электронного газа в полевом транзисторе с цилиндрическим затворным электродом // Радиотехника и электроника. 2010. Т. 55. № 11. C. 1376 - 1386.
5. Weaire D., Wherrett D.S., Miller D.A.B., Smith S.D. Effect of low-power nonlinear refraction on laser-beam propagation in InSb // Optics Letters. 1979. Vol. 4. N. 10. P. 331.