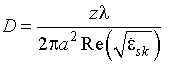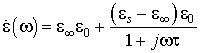ТЕПЛОВОЕ ВОЗДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН НА КОЖУ ЧЕЛОВЕКА

В. В. Штыков, А. А. Кальщиков

Национальный исследовательский университет «МЭИ»

 

Получена 18 сентября 2013 г.

 

Аннотация. Рассматривается вопрос о воздействии электромагнитного излучения на кожу человека. Найдено распределение в коже человека электромагнитного поля, а также распределение температуры, которое вызвано ее облучением. Задача решается с использованием теории линий передачи. Слои кожи человека заменены эквивалентными отрезками регулярной линии. Полученные результаты позволяют определить частоты, на которых воздействие электромагнитных волн является максимальным.

Ключевые слова: кожа человека, электромагнитное воздействие.

Abstract:  The impact of electromagnetic radiation on human skin is discussed. The distribution of electromagnetic field in human skin, as well as the distribution of temperature, which is caused by its exposure, is found. The task is solved with the theory of transmission lines. Layers of human skin are replaced by equivalent segments of regular lines. The obtained results allow to determine the frequency at which the impact of electronic waves is the maximum.

Key words: Human skin, impact of electromagnetic radiation.

Введение

В современном мире человек подвергается интенсивному воздействию высокочастотных электромагнитных волн. Источниками электромагнитных возмущений являются предметы быта: мобильная связь, радиотелефония; также и промышленное оборудование: радиоретрансляторы, высокомощные радиопередатчики, радиолокаторы, линии электропередач и т.п. Возникает вопрос: безопасны ли данные источники излучения, а если есть опасность, то в чём она проявляется? Данное исследование позволяет раскрыть лишь одну часть вопроса, а именно то, какое тепловое воздействие оказывают электромагнитные возмущения на первый механизм защиты человека – его кожу.

В связи с этим рассмотрим нормальное падение на кожу человека электромагнитной волны (ЭМВ) с частотой  и со средней плотностью потока мощности .

Требуется определить математическую модель кожи человека и найти распределение в кожном покрове – электрического поля , средней поглощённой мощности тепловых потерь  и температуры .

 

1. Модель кожи человека

Для исследования воздействия ЭМВ на кожу человека, она представляется в виде слоистой структуры, имеющей пять слоёв: роговой, эпидермис, дерма, гиподерма и мышцы.

Использованная в [1] теория ориентационной поляризации даёт зависимость комплексной диэлектрической проницаемости  от частоты воздействующей ЭМВ, с учётом постоянной времени релаксации  в следующем виде

.

 

Здесь – относительная диэлектрическая проницаемость при бесконечной частоте; – статическая относительная диэлектрическая проницаемость;  Ф/м – электрическая постоянная.

 

Таблица 1. Параметры кожи человека

Слой кожи	Толщина, мм			, пс
Роговой слой	0.05	60.0	3.0	10.0
Эпидермис	1.5	58.0	3.0	9.4
Дерма	4.0	45.0	4.0	8.0
Гиподерма	10.0	14.7	2.6	7.9
Мышцы		50.0	4.0	10.6

 

В табл. 1 приведены параметры кожного покрова, полученные из [2-4] и использованные нами для расчетов.

Для нахождения распределения поглощённой мощности в каждом слое кожи человека нам необходимо знать зависимость относительной проводимости от частоты ЭМВ – . Она равна

.

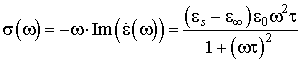Модуль относительной диэлектрической проницаемости и удельная проводимость каждого слоя существенным образом зависят от частоты, и каждый из них различно реагирует на ЭМВ. В качестве примера в табл. 2 приведены значения параметров на частоте 3 ГГц.

Таблица 2. Параметры кожи человека на частоте 3 ГГц

		, См/м
Роговой слой	58.96	1.73
Эпидермис	57.11	1.58
Дерма	44.50	1.01
Гиподерма	14.55	0.29
Мышцы	49.04	1.47

 

2. Распределение электрического поля

В подавляющем числе случаев применения СВЧ и КВЧ излучения в биологии и медицине объект находится в непосредственной близости, а иногда и в прямом контакте с облучателем, т.е. в зоне Френеля антенны. В этом случае  пучки Гаусса-Эрмита нулевого порядка описывают поля с высокой степенью точности. Медленно меняющуюся вдоль продольной оси комплексную амплитуду пучка внутри кожного покрова можно записать в следующей форме [1]:

 

,

где

[1]–

безразмерная дифракционная длина, a – апертура пучка в плоскости x0y,  – действительная часть относительной комплексной диэлектрической проницаемости кожи.

Если , то изменением в процессе распространения распределения поля пучка в поперечном сечении можно пренебречь. В явной форме это возможно при условии

.

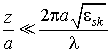Учитывая, что , получаем

.

 

Даже если апертура пучка равна длине волны, до глубины в десяток длин волн поперечное распределение поля можно считать неизменным, что характерно для регулярных линий передачи. Таким образом, для нахождения распределения комплексной амплитуды электрического поля  можно представить каждый слой в виде эквивалентного отрезка регулярной линии передачи.

На границах раздела двух слоёв комплексная постоянная распространения  претерпевает разрыв первого рода. На основании теории цепей с распределенными параметрами [5] распределение электрического поля  в каждом i–м слое длиной  в системе координат связанной с этим слоем можно записать следующим образом:

.

 

Рис. 1. К решению задачи о распределении поля

 

Для каждого слоя имеется

,

коэффициент отражения

,

характеристическое сопротивление

,

 

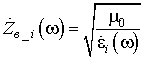а комплексное сопротивление нагрузки равно входному сопротивлению всех слоев, которые следуют за i-тым

 

.

Неизвестная величина  связана с известным значением напряжённости электрического поля на входе  следующим образом

 

.

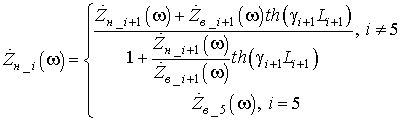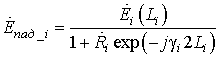Связь электрического поля E между двумя отрезками линии .

Распределение модуля напряжённости электрического поля меняется с изменением частоты. Наглядное представление частотно-пространственных зависимостей даёт рис. 2.

 

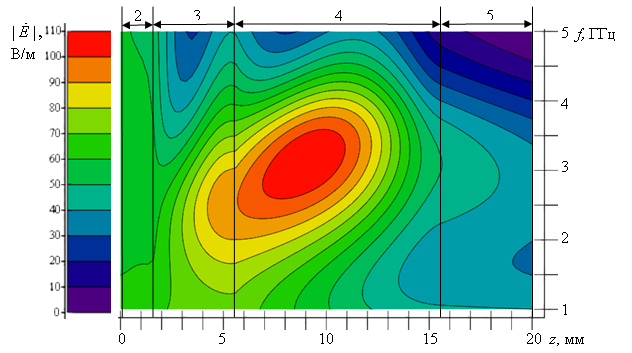
Рис. 2. Частотно-пространственная зависимость модуля напряжённости электрического поля. 2..5 – слои кожного покрова. Первый слой кожного покрова слишком тонок и поэтому не показан.

На рис. 2 видно, что в гиподерме сосредотачивается максимум напряжённости электрического поля. Своё максимальное значение модуль напряжённости электрического поля принимает на частоте около 3 ГГц. Оно расположено на глубине около 10 мм.

Амплитуда поля падает на почти два порядка на глубине 20мм. Это означает, что использование модели линии передачи оправданно. С повышением частоты ситуация будет только улучшаться.

 

3. Распределение мощности тепловых потерь

Удельная поглощённая мощность связывается с электрическим полем и параметрами среды выражением

.

 

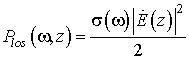Распределение в пространстве поглощённой мощности сильно меняется с изменением частоты. Наглядное представление частотно-пространственной зависимости даёт рис. 3.

 

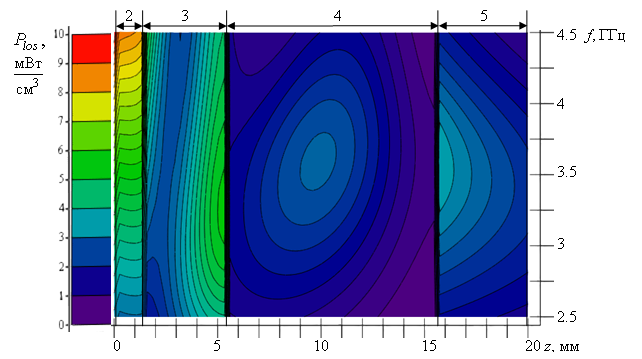
Рис 3. Частотно-пространственная зависимость удельной поглощённой мощности, при среднем потоке мощности . 2..5 – слои кожного покрова

На рис. 3 видно, что максимум удельной поглощённой мощности приходится на первые два слоя кожного покрова. В противоположность рис. 2 на гиподерму не приходится максимум удельной поглощённой мощности. Это объясняется тем, что гиподерма обладает минимальной удельной проводимостью по сравнению с другими слоями (см. таблицу 2).

Так как первые слои кожного покрова достаточно узкие, то для наглядности приведем зависимость удельной поглощённой мощности от продольной координаты z на заданной частоте.

На рис. 4 видно, что источники тепла будут в основном располагаться в дерме, гиподерме и мышцах. Поэтому первые два слоя, роговой и эпидермис, не оказывают значительного влияния ввиду их малой толщины.

 

Рис 4. Зависимость удельной поглощённой мощности от продольной координаты z, при среднем потоке мощности  и на частоте . 1..5 – слои кожного покрова

4. Распределение температуры

По известному распределению мощности тепловых потерь, решая стационарное, неоднородное уравнение теплопроводности, можно найти распределение температуры в коже человека. Численное решение этого уравнения не представляет трудности. Однако имеет смысл несколько упростить задачу для того, чтобы получить общее представление о распределении температуры в кожном покрове. Будем полагать, что распределение температуры однородно по сечению пучка электромагнитной волны. Это тем более справедливо, чем выше коэффициент поперечной теплопроводности. Последняя, по-видимому, выше из-за кровотока.

Одномерное уравнение теплопроводности в стационарном случае имеет вид

 

.                                         (1)

 

Здесь коэффициент теплопроводности , согласно [6], принимает значение около 0.5 Вт/(мК).

Уравнение (1) представляет собой неоднородную краевую задачу. Для её однозначного решения необходимо определить граничные условия.

Будем считать, что внешняя среда имеет бесконечно большое тепловое сопротивление, и поэтому температура на поверхности кожи человека . Будем полагать, что на максимально исследуемой глубине  температура постоянна и принимает значение .

Для упрощения расчётов преобразуем краевую задачу так, чтобы граничные условия оказались однородными.

Выполним замены, имеющие следующий вид

,

,

.

 

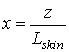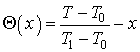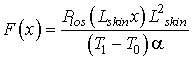При этом уравнение (1) примет вид

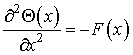,                                (2)

 

а граничные условия примут вид

.                                    (3)

 

Таким образом, приходим к неоднородной краевой задаче (2) с однородными граничными условиями (3), решение которой, может быть получено через функцию Грина –  следующим образом [7]

.                (4)

 

Здесь

.

 

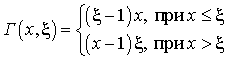Тогда, с учётом выражения (4) и сделанных замен находим распределение температуры

.

 

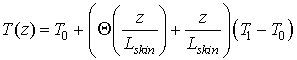На рис. 5 показано распределение температур в кожном покрове человека в двух случаях: при воздействии на него электромагнитным полем и без воздействия.

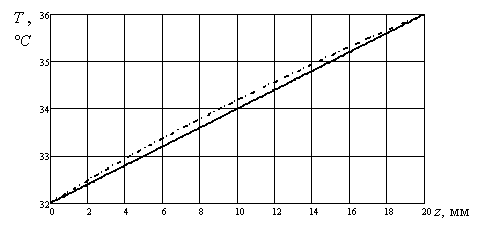
Рис. 5. Распределение температуры вдоль продольной координаты z, при среднем потоке мощности  и на частоте . Штрихпунктирная кривая – распределение температуры при воздействии электромагнитного поля. Сплошная линия – без воздействия электромагнитного поля

 

Рис. 6. Распределение изменения температуры в зависимости от продольной координаты z, при среднем потоке мощности  и на частоте. 2..5 –слои кожного покрова

При потоке мощности отклонение температуры невелико. Поэтому, на рис. 6 показано распределение изменения температуры в кожном покрове человека, при воздействии на него ЭМВ.

Видно, что максимальное изменение температуры происходит в области дермы и гиподермы. Отсутствие явно выраженных пиков объясняется тем, что уравнение теплопроводности обладает сглаживающим свойством.

6. Обсуждение результатов

Изложенный метод расчёта позволяет провести исследование свойств кожного покрова в широком диапазоне параметров. Однако, надо иметь в виду следующее.

Характер частотных зависимостей определяется толщинами слоёв кожного покрова, значениями диэлектрической проницаемости и удельной проводимости каждого из них.

Согласно [6] температурный коэффициент изменения параметров слоев кожи составляет величину порядка 1% на градус. Следовательно, при плотностях мощности излучения порядка  отклонения от исходных значений не превышают десятых долей процента. Но при плотности потока порядка , по-видимому, уже нельзя ограничиваться линейным приближением.

 

Литература

1.    Вайнштейн Л. А. Электромагнитные волны. - М: Радио и связь 1988.

2.    А. Н. Кузнецов. Биофизика электромагнитных воздействий: (Основы дозиметрии). – М.: Энергоатомиздат, 1994.

3.    A. M. Campbell. Measurements and analysis of the microwave dielectric properties of tissues, PhD thesis, Glasgow University, 1990.

4.    K. M. Yaws, D. G. Mixon, W. P. Roach. Electromagnetic properties of tissue in the optical region, air force research laboratory, 2007.

5.    Д. В. Николаев, А. В. Смирнов, И. Г. Бобринская, С. Г. Руднев. Биоимпедансный анализ состава тела человека. – М.: Наука, 2009.

6.    С. И. Баскаков. Радиотехнические цепи с распределёнными параметрами: Учебное пособие для вузов. – М.: Высшая школа, 1980.

7.    F. Gustrau, A. Bahr. Final Report: Biological Effects in the cm/mm Wave Range Part II/III Determination of Material Parameters and Analysis of Field Strengths in Human Tissue By Institute of Mobile and Satellite Communication Techniques GmbH, Germany, 1998.

8.    Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. Пер. с нем. – 4-е изд., испр. – М.: Наука, 1971.

---

[1] Точнее