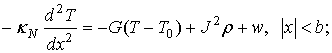оценка Поглощенной мощности гетеродина для сверхпроводниковых смесителей на основе пленок NbN в рамках модели горячего пятна
C. А. Рябчун, И. В. Третьяков, А. И. Кардакова, А. В. Семенов, Ю. В. Лобанов, С. В. Селиверстов, А. В. Трифонов, А. В. Масленникова
Московский педагогический государственный университет
Получена 29 августа 2013 г.
Аннотация. В статье обсуждается модель горячего пятна для смесителя на эффекте электронного разогрева в сверхпроводящих пленках нитрида ниобия применительно к оценке поглощенной мощности гетеродина. Показано, что по достижении определенной длины чувствительного элемента смесителя поглощенная мощность перестает зависеть от его длины.
Ключевые слова: эффект электронного разогрева в сверхпроводниках, гетеродинные приемники, поглощенная мощность гетеродина.
Abstract: The paper discusses the hot-spot model of the superconducting hot-electron bolometer applied to the estimation of the absorbed local oscillator power. As the length of the sensitive element is decreased the absorbed power becomes length-independent.
Key words: hot-electron effect in superconductors, heterodyne receivers, absorbed local oscillator power.
Введение
Терагерцовый диапазон частот, условно простирающийся от 102 ГГц до 104 ГГц, в последнее время привлекает к себе много внимания. Причина этого в том, что данный диапазон интересен с точки зрения практических устройств, работающих здесь. Это системы безопасности, построения изображения, обнаружения взрывчатых веществ и наркотиков, а также системы для медицинской диагностики [1]. Кроме того, более 50% электромагнитного излучения, приходящего на Землю из окружающего пространства содержит ценную информацию в терагерцовом диапазоне [2], поэтому он представляет огромный интерес для радиоастрономии.
На частотах выше 1 ТГц безусловными лидерами среди гетеродинных (когерентных) приемников являются смесители на эффекте электронного разогрева в сверхпроводниковых пленках [3,4,5]. Данный эффект обусловлен тем, что при гелиевых температурах (около 4 К) время взаимодействия электронов в металле между собой существенно короче времени взаимодействия электронов с колебаниями решетки (с фононами), что позволяет с хорошей степенью точности рассматривать электронную и фононную подсистемы металла раздельно [3]. В результате поглощения металлической пленкой электромагнитного излучения температура электронов становится выше температуры фононов, и тогда говорят о разогреве электронной подсистемы и описывают ее функцией распределения Ферми с некоторой эффективной температурой, которая отличается от температуры фононов [6]. В результате электрон-фононного взаимодействия электроны отдают решетке избыточную энергию, а она в свою очередь передается подложке, на которую нанесена пленка. Этот механизм релаксации электронной подсистемы называется фононным охлаждением [7]. Если же разогретые электроны в среднем успевают покинуть пленку, так и не успев провзаимодействовать с решеткой, то говорят, что реализовано диффузионное охлаждение электронной подсистемы [8]. Какой из двух механизмов будет доминирующим, зависит от размеров пленки и от параметров материала (коэффициент диффузии, характерные времена и теплоемкости).
2. Оценка поглощенной мощности гетеродина в модели горячего пятна
Для описания работы смесителя на эффекте электронного разогрева используют две модели: модель однородного разогрева [9] и модель горячего пятна [10]. Как следует из названия, в модели однородного разогрева предполагается, что температура пленки не зависит от координаты. В приближении малого сигнала, когда поглощенное пленкой излучение вызывает лишь незначительное изменение электронной и фононной температур по сравнению с температурой подложки, соответствующие уравнения становятся линейными и допускают аналитическое решение. Это позволяет получить выражение для частотной зависимости коэффициента преобразования смесителя, которая успешно используется для аппроксимации экспериментальных результатов и определения характерных времен релаксации [11].
В модели горячего пятна предполагается, что сверхпроводимость разрушена только в некоторой области (пятне) пленки, размер которой определяется протекающим током и мощностью поглощенного излучения (главным образом поглощенной мощностью гетеродина, поскольку мощность сигнала существенно меньше). В основе модели лежат уравнения теплового баланса, которые следует записать отдельно для нормальной и сверхпроводящей областей (рассматривается одномерный случай):
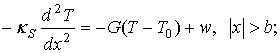 (1б)
(1б)
где T – электронная температура; T0 – температура фононов, равная температуре подложки; κN, κS – коэффициенты теплопроводности нормальной и сверхпроводящей областей соответственно; G – коэффициент теплоотвода между электронной подсистемой и фононной; J – плотность транспортного тока; ρ – удельное сопротивление; w – мощность поглощенного излучения; 2b – размер горячего пятна. При написании уравнений (1) сделан ряд предположений/упрощений:
1) Рассматривается одномерная ситуация.
2) Рассматривается режим малого сигнала. Это означает, что отклонения значений электронной и фононной температур от их соответствующих равновесных значений невелики, что позволяет линеаризовать уравнения.
3) Температура фононной подсистемы пленки равна температуре подложки. Строго говоря, это не так, но данное предположение справедливо в режиме малого сигнала и существенно упрощает решение задачи.
4) Коэффициенты теплоотвода взяты равными своим значениям при температуре подложки, т.е. в задаче они считаются постоянными. То же относится к удельному сопротивлению и коэффициентам теплопроводности, значения которых берутся при критической температуре в нормальной области и при температуре подложки в сверхпроводящей.
5) Падающее на пленку излучение одинаково поглощается как в нормальной области, так и в сверхпроводящей. Это справедливо, если энергия фотона больше или равна ширине энергетической щели сверхпроводника, что и реализуется на практике.
6) Протекание тока по сверхпроводнику может приводить к возникновению вихрей и центров проскальзывания фазы, что проявит себя в возникновении конечного сопротивления. Этими нетермическими эффектами мы пренебрегаем.
Уравнения (1) должны быть дополнены следующими граничными условиями:
![]() (2а)
(2а)
![]() (2б)
(2б)
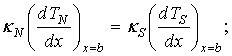 (2в)
(2в)
![]() (2г)
(2г)
![]() (2д)
(2д)
Условие (2а) есть просто выражение симметричности решения по отношению к середине пленки. Если контактные площадки достаточно массивные, то их температура равна температуре подложки – отсюда условие (2б), где 2a – размер мостика. Условие (2в) является следствием непрерывности потока тепла, а условие (2г) – следствием непрерывности температуры. Наконец, условие (2д) есть требование самосогласованности задачи и по существу определяет размер нормальной области (TC – температура сверхпроводящего перехода).
Решения уравнений (1) при условиях (2) выглядят следующим образом:
 (3а)
(3а)
 (3б)
(3б)
Здесь
введены характерные тепловые длины в нормальной и сверхпроводящей областях: ![]() и
и ![]() . Из условия самосогласованности следует связь между размером
нормальной области с одной стороны и величиной транспортного тока и мощностью
поглощенного излучения с другой:
. Из условия самосогласованности следует связь между размером
нормальной области с одной стороны и величиной транспортного тока и мощностью
поглощенного излучения с другой:
 . (4)
. (4)
Если уравнение (4) дополнить законом Ома
![]() , (5)
, (5)
то (4) и (5) вместе будут представлять собой параметрические уравнения вольт-амперной характеристики сверхпроводниковой полоски.
Для проведения численного моделирования полученных выражений необходимо учесть связь коэффициента теплоотвода от электронной подсистемы к фононной с электронной теплоемкостью и характерным временем остывания электронной температуры:
 , (6)
, (6)
где γ
= 1.84×10-4 Дж/см3/К – постоянная Зоммерфельда в NbN [12], τT ≈ 50 пс – время
остывания электронной подсистемы [13]. Удельное сопротивление ρ
можно определить из значения сопротивления пленки на квадрат RS, которое измеряется в процессе изготовления
смесителей и составляет примерно 500 Ом для пленок толщиной h = 3.5 нм: ![]() .
Критическая температура пленок NbN
обычно равна 9.5 К.
.
Критическая температура пленок NbN
обычно равна 9.5 К.
На рисунке 1 слева приведено семейство вольт-амперных характеристик (ВАХ) смесителя для различных уровней мощности гетеродина; самая нижняя ВАХ соответствует оптимальному уровню мощности. На том же рисунке справа приведена зависимость оптимального уровня мощности от длины чувствительного элемента смесителя (для согласования с планарной антенной выдерживается отношение длины смесителя к его ширине, равное 1:10).
Приведенные на рисунке 1 зависимости качественно согласуются с экспериментом. Количественные расхождения связаны, по-видимому, с допущениями, сделанными выше. Зависимость поглощенной мощности от длины смесителя близка к квадратичной. Качественно это можно объяснить тем, что поглощенная мощность пропорциональна площади пленки, а она – квадрату длины. Когда длина чувствительного элемента смесителя становится сравнимой с тепловой длиной, становится эффективным диффузионное охлаждение, поэтому дальнейшее уменьшение размеров практически не влияет на величину мощности.
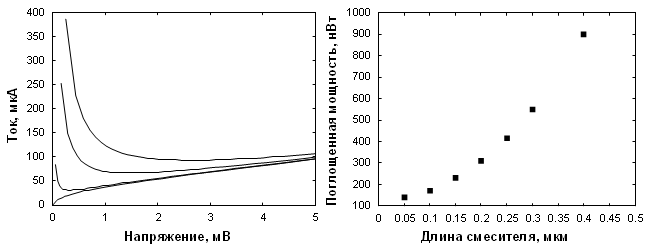
Рисунок 1.
Слева: семейство ВАХ смесителя для различных уровней мощности гетеродина;
самая
нижняя ВАХ соответствует оптимальному уровню мощности.
Справа: зависимость
оптимального уровня мощности гетеродина от длины чувствительного элемента
(длины смесителя).
3. Выводы
В рамках модели горячего пятна для смесителя на эффекте электронного разогрева в сверхпроводниках получена зависимость оптимальной поглощенной мощности гетеродина от длины чувствительного элемента смесителя. При уменьшении длины до величины, сравнимой с характерной тепловой длиной сверхпроводниковой пленки, зависимость становится более пологой, и дальнейшее уменьшение размеров чувствительного элемента практически не влияет на величину мощности.
Работа выполнена в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг., государственный контракт № 16.740.11.0580 от 30 мая 2011 г., а также при поддержке гранта Президента Российской Федерации, договор № 16.120.11.4005-МК от 01.02.2012.
Литература
1. A. Rostami, H. Rasooli, H. Baghban. Terahertz technology: fundamentals and applications // Springer-Verlag. – Berlin, Heidelberg: 2011.
2. Scientific motivation and technology requirements for the SPIRIT and SPECS far-infrared/submillimeter space interferometers / D. T. Leisawitz, W. C. Danchi, M. J. DiPirro, L. D. Feinberg, D. Y. Gezari, M. Hagopian, W. D. Langer, J. C. Mather, S. H. Moseley, Jr., M. Shao, R. F. Silverberg, J. G. Staguhn, M. R. Swain, H. W. Yorke, X. Zhang // Proc. SPIE. 4013, UV, Optical, and IR Space Telescopes and Instruments – Munich, Germany: 2000. – p. 36.
3. Смеситель миллиметрового и субмиллиметрового диапазонов волн на основе разогрева электронов в резистивном состоянии сверхпроводниковых пленок / М. Гершензон, Г. Н. Гольцман, И. Г. Гогидзе, Ю. П. Гусев, А. И. Елантьев, Б. С. Карасик, А. М. Люлькин, А. Д. Семенов // СФХТ. – 1990. – том 3, часть I. – стр. 2143-2160.
4. Hot-electron bolometer terahertz mixers for the Herschel Space Observatory / S. Cherednichenko, V. Drakinskiy, T. Berg, P. Khosropanah, and E. Kollberg // Review of Scientific Instruments. – 2008. – 79. – 034501.
5. John R. Tucker, Marc J. Feldman. Quantum detection at millimeter wavelengths // Rev. Mod. Phys. – 1985. – vol. 57. – p. 1055.
6. Разогрев квазичастиц в сверхпроводящей пленке, находящейся в резистивном состоянии / Е. М. Гершензон, М. Е. Гершензон, Г. Н. Гольцман, А. Д. Семенов, А. В. Сергеев // Письма в ЖЭТФ. – 1981.
7. E. M. Gershenzon et al., Supercond., Phys. Chem. Technol. 3,. 1582 (1990).
8. D. Prober. Superconducting terahertz mixer using a transition-edge microbolometer // Appl.Phys.Lett. – 1993. – vol. 62, issue 17. – p. 2119.
9. N. Perrin, C. Vanneste. Response of superconducting films to a perodic optical irradiation // Phys. Rev. B – 1983. – vol. 28. – pp. 5150-5160.
10. Hotspot mixing: A framework for heterodyne mixing in superconducting hot-electron bolometers / D. Wilms Floet, E. Miedema, T. M. Klapwijk, and J. R. Gao // Applied Physics Letters – 1999. – 74. – p. 433.
11. Analysis of the Noise Performance of the Hot-Electron Superconducting Bolometer Mixer / B. S. Karasik, A. I. Elantiev // Proceedings of the 6th International Symposium on Space Terahertz Technology / California Institute of Technology – Pasadena, CA, USA: 1995. – p. 229.
12. Broadband ultrafast superconducting NbN detector for electromagnetic radiation / Yu. P. Gousev, G. N. Gol’tsman, A. D. Semenov, E. M. Gershenzon, R. S. Nebosis, M. A. Heusinger, and K. F. Renk // Applied Physics Letters – 1994. – 75. – p. 3695.
13. Low noise and wide bandwidth of NbN hot-electron bolometer mixers / I. Tretyakov, S. Ryabchun, M. Finkel, A. Maslennikova, N. Kaurova, A. Lobastova, B. Voronov, and G. Gol’tsman // Applied Physics Letters. – 2011. – 98. – 033507.