УДК 621.372, 532.59
О ТЕСТИРОВАНИИ ЧИСЛЕННЫХ МЕТОДОВ ДЛЯ ПОЛУЧЕНИЯ ОСЦИЛЛИРУЮЩИХ РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В. Н. Бирюков, Л. Е. Гатько
Южный федеральный университет
Статья получена 17 сентября 2015 г.
Аннотация: Дифференциальное уравнение Дуффинга может быть одновременно и жестким и быстро осциллирующим. Аналитическое решение уравнения известно, поэтому его удобно использовать для оценки эффективности численных методов решения дифференциальных уравнений. Показано, что свойства методов при повышении жесткости изменяются по сравнению с частным случаем – уравнением гармонического осциллятора.
Ключевые слова: осциллятор, быстро осциллирующие задачи, обыкновенные дифференциальные уравнения, численные методы.
Abstract. This paper exploits a concurrently stiff and highly oscillatory differential Duffing equation and discusses some numerical methods to solve it. The local error, the global error, and the error of solutions’ amplitude and period are examined.
Keywords: oscillating circuits, stiff differential equations, numerical methods, error analysis.
Введение
Задача Коши для систем обыкновенных дифференциальных уравнений (СОДУ) можно условно разделить на следующие типы: мягкие, жесткие, плохо обусловленные и быстро осциллирующие [1]. В работе [2] констатируется, что точное математическое определение термина «быстро осциллирующие системы» отсутствует. Ниже под быстро осциллирующей подразумевается задача, имеющая собственные значения матрицы Якоби на мнимой оси, или, по крайней мере, расположенные весьма близко к ней. Физическим объектом в данном случае служит или простейшая колебательная система без демпфирования, например LC–цепь, или автогенератор на основе LC–цепи с малым по модулю последовательным дифференциальным сопротивлением.
Для тестирования численных методов решения осциллирующих задач используются или линейный гармонический осциллятор [2], или осциллятор Ван дер Поля [3], или осциллятор с полигональной нелинейностью [4, 5]. В первом и последнем случаях точное решение известно. Аналитического решения осциллятор Ван дер Поля не имеет, но существует большое количество публикаций о расчете амплитуды и периода колебаний [6–8]. Нелинейный осциллятор может обладать сколь угодно большой жесткостью в режиме релаксационных колебаний, но собственные значения матрицы Якоби при этом становятся вещественными.
Реальные устройства, которые можно назвать быстро осциллирующими, описываются СОДУ высоких порядков. Эти СОДУ обычно оказываются жесткими, поэтому свойства численных методов решения СОДУ оценивают не только на простейших тестовых СОДУ 2-го порядка, но и путем анализа реальных устройств – транзисторных автогенераторов [9], однако в этом случае количественной оценки свойств используемых численных методов получить не удается.
В настоящей работе для анализа свойств численных методов предлагается математическая модель недемпфированного нелинейного осциллятора, описываемого уравнением Дуффинга. Собственные значения якобиана лежат в данном случае на мнимой оси, а жесткость определяется существенной негладкостью решения. Использование уравнения Дуффинга таким образом позволяет в какой-то мере оценивать свойства численных методов решения СОДУ одновременно и жесткой и быстро осциллирующей задач Коши. Жесткость уравнения Дуффинга можно задавать произвольно, в частном случае уравнение Дуффинга совпадает с уравнением гармонического осциллятора.
2. Решение уравнения Дуффинга
Кубическое уравнение Дуффинга в общем виде имеет вид [10,11]
где δ, α, β - константы, f(t) - функция внешнего воздействия.
В
частном случае при δ = 0,
α = 1, β = 1, y(0) = Y0
,  уравнение Дуффинга имеет аналитическое
решение [9, 10]
уравнение Дуффинга имеет аналитическое
решение [9, 10]
![]() ,
,
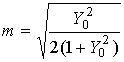 .
.
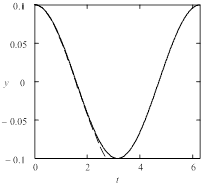
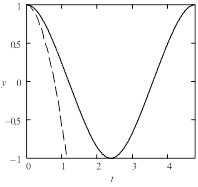
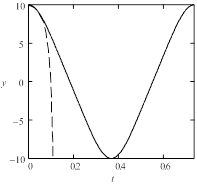
На рис. 1 представлены решения уравнения (1) на одном периоде для случая малой, средней и высокой жесткости. О росте жесткости можно судить по уменьшению радиуса сходимости аппроксимирующего решение степенного ряда. Амплитуда периодического решения задается начальным значением Y0, а период колебания определяется выражением
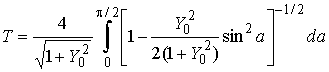 .
.
|
a |
б |
в |
|
Рис. 1. Решение уравнения Дуффинга при различных начальных условиях: а) Y0 = 0,1, б) Y0 = 1, в) Y0 = 10. Штриховая линия – аппроксимация решения отрезком ряда Тейлора 16-го порядка. |
||
Периодический характер решения позволяет произвести оценку погрешности численного решения по параметрам колебания – амплитуде и периоду. Текущие относительные погрешности оценки периода и амплитуды соответственно определялись как
![]() и
и 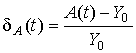 .
.
Для оценки текущего периода колебаний T(t) использовалась линейная интерполяция численного решения в точках изменения знака y(t), для оценки текущей амплитуды A(t) – квадратичная в точках локальных экстремумов.
При малой жесткости указанные зависимости, как и следовало ожидать, весьма близки к соответствующим зависимостям гармонического осциллятора. В данном случае погрешность решения определяется опцией tol и слабо зависит от выбранного шага. При высокой жесткости задачи наоборот текущая погрешность амплитуды численного решения от значения tol зависит значительно слабее, чем от шага решения. Последнее можно объяснить тем, что точность численного решения оценивается программой локальной погрешностью, а глобальная погрешность в сингулярно-возмущенных задачах связана с локальной весьма слабо.
|
|
|
|
|
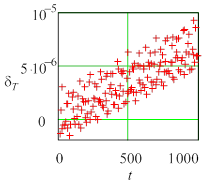
Рис. 2. Текущие погрешности амплитуды колебаний для нежесткой задачи (Y0 = 0,1) метода Radau5; а) tol =10 – 6, h= 0.0610352, б) tol=10 – 7 h= 0.0610352, в) tol = 10 – 6. h= 0,0305176. |
||
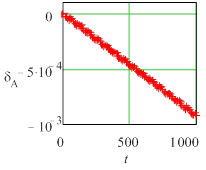
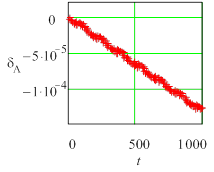
Во всех случаях погрешность состоит из двух составляющих – быстрой и медленной. Медленная составляющая имеет тот же смысл, что и коэффициенты демпфирования (для амплитуды) и фазовый коэффициент (для периода), используемые в анализе Р-устойчивости [2]. Быстрая составляющая определяется, по-видимому, ошибкой округления и существенно растет с увеличением жесткости
|
|
|
|
|
Рис. 3 Текущие погрешности амплитуды колебаний для жесткой задачи (Y0 = 10) метода Radau5; а) tol =10 – 6, h = 0,0610352, б) tol = 10 – 7, h =0,0610352, в) tol = 10 – 6, h = 0,0305176. |
||
Относительная погрешность определения периода при любой жесткости оказывается существенно меньше погрешности амплитуды, причем уменьшение шага влияет на точность определения периода слабее, чем изменение опционной погрешности tol .
|
|
|
|
|
Рис.4. Текущие погрешности периода колебаний для нежесткой задачи (Y0 = 0,1) метода Radau5; а) tol = 10 – 6, h= 0,0610352, б) tol = 10 – 7, h = 0,0610352, в) tol = 10 – 6, h = 0,0305176. |
||
|
|
|
|
|
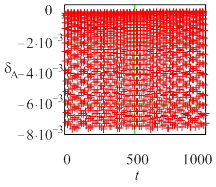
Рис. 5. Текущие погрешности периода колебаний для жесткой задачи (Y0 = 10) метода Radau5; а) tol =10 – 6, h = 0,0610352, б) tol = 10 – 7, h = 0,0610352, в) tol = 10 – 6, h = 0,0305176 |
||
Для сравнения на Рис. 6 и 7 приведены графики текущих значений погрешности параметров для случая сильной жесткости, полученные многошаговым методом, применяющим формулы дифференцирования назад (ФДН). Если погрешности двух методов близки, то знаки медленной составляющей погрешностей оказались разными. Отметим, что решение методом ФДН, который используется практически во всех симуляторах электронных цепей, при сильной жесткости формально расходится.
|
|
|
|
|
Рис.6. Текущие погрешности амплитуды колебаний для жесткой задачи (Y0 = 10) метода ФДН; а) tol =10 – 6, h = 0,0610352, б) tol = 10 – 7, h = 0,0610352, в) tol = 10 – 6. h= 0,0305176. |
||
|
|
|
|
|
Рис.
7. Текущие погрешности периода колебаний для жесткой задачи (Y0 = 10)
метода ФДН; а) tol
=10 – 6, h =
0,0610352, б) tol =10
– 7, h =
0,0610352, |
||
3. Об оценке свойств численных методов на задаче гармонического осциллятора
а) Локальная погрешность
Для
рассмотрения особенности локальной погрешности на мнимой оси проанализируем,
как меняется абсолютная погрешность метода на одном шаге численного решения в
зависимости от аргумента комплексной константы λ в
тестовой задаче Далквиста ![]() [12].
[12].
Рассмотрим решение системы ОДУ второго порядка
с
вещественными коэффициентами a11 = –
r, a12 = – 1,
a21 = – 1 ,
a22 = 0
и собственными значениями ![]() . Далее полагается, в
диапазоне 0 ≤ r < 1
собственные значения λ принимают вид
. Далее полагается, в
диапазоне 0 ≤ r < 1
собственные значения λ принимают вид ![]() ,
где
,
где ![]() . Решение СОДУ для первой
переменной при начальных условиях
. Решение СОДУ для первой
переменной при начальных условиях ![]() имеет вид
имеет вид ![]()
На рис. 8 – 9 приведены графики локальной погрешности, соответствующие неявным разностным схемам трапеций
![]()
и схеме, полученной из формулы дифференцирования назад второго порядка путем использования на первом частичном шаге метода трапеций
![]() ,
,
где ![]() .
.
Графики построены в широком диапазоне
шагов интегрирования, что позволяет оценивать не только асимптотическую
погрешность метода, но и его L-устойчивость.
Полученные результаты свидетельствуют о том, что константа асимптотической погрешности
метода существенно зависит от аргумента λ: ![]() .
При
.
При ![]() , то есть при
, то есть при ![]() , полученные результаты совпадают с
результатами, получаемыми на задаче Далквиста
, полученные результаты совпадают с
результатами, получаемыми на задаче Далквиста ![]()
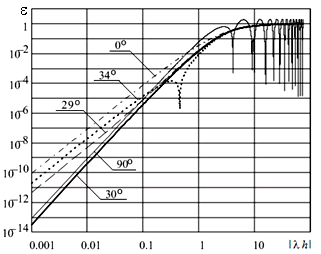
Рис. 8. Зависимость локальной погрешности неявного
метода трапеций от шага
для ряда аргументов собственных значений матрицы
коэффициентов А.
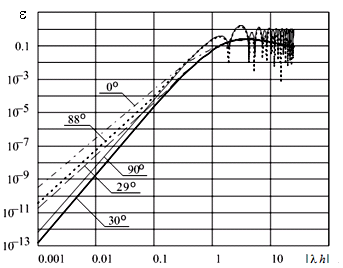
Рис.
9. Зависимость локальной погрешности неявного метода Tр-ФДН2
от шага
для ряда аргументов собственных значений матрицы коэффициентов А.
Известно, что на мнимой оси (то есть при α = 90○.) погрешность численных методов решения ОДУ может иметь особенность [13]. Однако, анализ зависимости локальной погрешности от аргумента собственного значения матрицы А показал, что такая особенность не является единственной: у неявного метода Эйлера порядок метода повышается на единицу при α = 45○, а у рассмотренных методов 2-го порядка при α = 90○ и α = 30○. Причина особенности очевидна: у решения тестовой задачи с изменением α изменяются все производные и в особой точке совпадают соответствующие производные точного решения и разностной схемы, не совпадающие при остальных значениях α. Полученные результаты позволяют сделать вывод о том, что при изменении аргумента собственных значений матрицы А изменяется не только константа асимптотической погрешности, но и порядок точности метода. Увеличение порядка в особых точках при α = 90○ имеет значение при анализе Р-устойчивости метода, а также при анализе свойств вложенных методов, позволяющих кроме решения получить и оценку локальной погрешности, поскольку вблизи от особых точек эта оценка будет несостоятельной.
Таким образом, асимптотическая погрешность метода для быстро осциллирующих задач имеет специфический вид. Отметим, что рассмотрение локальной погрешности разностной схемы на комплексной плоскости служит дополнением к методу сравнения численного решения с точным с помощью порядковых звезд [3].
б) Глобальная погрешность
Поскольку точное решение линейного недемпфированного осциллятора
известно, то его уравнение удобно использовать для тестирования численных
методов анализа. В этом случае свойства численных методов можно описать двумя
параметрами – коэффициентами демпфирования и фазы [2]. Однако существует возможность сравнения методов на этой
задаче традиционным способом – с помощью глобальной погрешности. Если выбрать в
(2) r = 0, чтобы решением служила косинусоида, то на интервале
наблюдения точно равном периоду колебания наклон зависимости глобальной
погрешности ![]() от шага не обязательно совпадает с порядком точности метода. Наклон
от шага не обязательно совпадает с порядком точности метода. Наклон ![]() P-устойчивого метода трапеций 2-го порядка с нулевым
демпфированием при выбранных условиях равен четырем (см. Рис. 10). Увеличение
асимптотического (для малых h) порядка метода для данного частного случая возможно и для
методов, граница области устойчивости которых не совпадает с мнимой осью. Таким
же наклоном
P-устойчивого метода трапеций 2-го порядка с нулевым
демпфированием при выбранных условиях равен четырем (см. Рис. 10). Увеличение
асимптотического (для малых h) порядка метода для данного частного случая возможно и для
методов, граница области устойчивости которых не совпадает с мнимой осью. Таким
же наклоном ![]() , как и метод трапеций, обладает и одношаговый L-устойчивый
метод, полученный из формулы дифференцирования назад четвертого порядка путем
использования на первом частичном шаге метода трапеций, на втором – ФДН второго
порядка, на третьем – ФДН четвертого порядка и на четвертом – ФДН четвертого
порядка [14]. У метода, основанного на ФДН
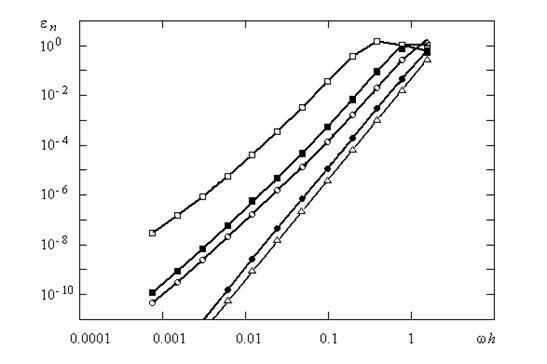
второго порядка, порядок наклона зависимости ε n (ωh) остается вторым. Интересно, что при двух и трех частичных шагах
одношагового метода, полученного из ФДН, наклон зависимости
, как и метод трапеций, обладает и одношаговый L-устойчивый
метод, полученный из формулы дифференцирования назад четвертого порядка путем
использования на первом частичном шаге метода трапеций, на втором – ФДН второго
порядка, на третьем – ФДН четвертого порядка и на четвертом – ФДН четвертого
порядка [14]. У метода, основанного на ФДН
второго порядка, порядок наклона зависимости ε n (ωh) остается вторым. Интересно, что при двух и трех частичных шагах
одношагового метода, полученного из ФДН, наклон зависимости ![]() равен трем.
равен трем.
|
|
|
Рис. 10. Зависимость глобальной погрешности от шага методов 2-го порядка на интервале Т = 2 π: □ – метод ФДН2, ■ –метод трапеций-ФДН2, ○ – метод трапеций-ФДН2-ФДН3, ● – метод трапеций-ФДН2-ФДН3-ФДН4, Δ – метод, состоящий из четырех одинаковых частичных шагов методом трапеций (наклон не зависит от числа частичных шагов). |
Обсуждение глобальной погрешности задачи Дуффинга представляет самостоятельный интерес и в данной работе не приводится.
Отметим, что замена оценки свойств численного метода на мнимой оси с помощью двух новых параметров [2] – коэффициентов демпфирования и фазы – одним известным – порядком погрешности – имеет методическую ценность, поскольку соответствует принципу entia non sunt multiplicanda sine necessitate.
4. Обсуждение результатов и выводы
Решение дифференциального уравнения в форме Коши всегда можно представить в виде степенного ряда. Если этот ряд сходится с требуемой точностью на заданном интервале (здесь на полупериоде), то уравнение может считаться не жестким. Используемое в настоящей работе определение жесткости не противоречит предложенному, например, в [15]. При малых Y0 (1) совпадает с уравнением недемпфированного гармонического осциллятора и теряет жесткость. В этом случае его решение в виде разложения в степенной ряд на полупериоде может быть получено с двумя десятками точных значащих цифр. С увеличением Y0 решение становится существенно не гладким и точность аппроксимации решения степенным рядом падает катастрофически.
Поскольку уравнение гармонического осциллятора является частным случаем уравнения Дуффинга, то анализ погрешности решения последнего позволяет получить более общие результаты, что важно при решении практических задач, – жестких и одновременно быстро осциллирующих. К таким задачам относятся, например анализ работы мощных колебательных радиотехнических цепей в импульсном режиме. Использование погрешностей параметров колебаний отличается от предложенного в [2] тем, что первые определяются не только разностной схемой, но и конкретной программой решения, включающей в себя оценку локальной погрешности и выбор шага решения.
Литература
1. Калиткин Н. Н. «Численные методы решения жестких систем», Математическое моделирование, 1995, т. 7, № 5, с. 8-11.
2. Petzold L. R., Jay L. O., Jeng Yen. Numerical solution of highly oscillatory ordinary differential equations // Acta Numerica. 1997, pp. 437 – 483
3. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999, 685 с.
4. Пилипенко А. М., Бирюков В. Н. Исследование эффективности современных численных методов при анализе автоколебательных цепей // Журнал радиоэлектроники, № 8, 2013. [Электронный ресурс]. URL: http://jre.cplire.ru/jre/aug13/9/text.pdf
5. Бирюков В. Н., Гатько Л. Н. «Точное стационарное решение уравнения автогенератора», Нелинейный мир, 2012, т. 10, № 9, с. 613-616.
6. Buonomo A., Di Bello C. Asymptotic formulas in nearly sinusoidal nonlinear oscillators // IEEE Trans. Circuits Systems I Fund. Theory Appl. 1996, Vol. 43, pp. 953-963
7. Najafi M., Moghimi M., Massah H. Analytical treatment for nonlinear oscillation equations and vibratory system of waves // Tamkang journal of mathematics, Vol. 40, No 1, 2009, pp. 77-94.
8. Koçak H., A. et al Comparative study of analytical solutions to the coupled Van-der-Pol’s non-linear circuits using the He’s method (HPEM) and (BPES). Circuits and Systems, 2011, 2, pp. 196-200 Published Online July 2011. // [Электронный ресурс]. URL: http://www.SciRP.org/journal/cs.
9. Maffezzoni P., Codecasa L., D’Amore D. Time-Domain Simulation of Nonlinear Circuits through Implicit Runge-Kutta Methods // IEEE Trans. Circuits and Syst. I, vol. 54, pp. 391-400, Feb. 2007.
10. Кузнецов А. П., Кузнецов С. П., Рыскин Н. М. Нелинейные колебания – М.: Изд-во физико-математической литературы, 2002. – 292 с.
11. Kargar A., Akbarzade M. Analytical Solution of Nonlinear Cubic-Quintic Duffing Oscillator Using Global Error Minimization Method //Adv. Studies Theor. Phys., Vol.6, 2012, no 10, 467-471
12. Бирюков В. Н., Применко К. Л. «К оценке локальной погрешности разностных схем», Материалы международной научной конференции «Информационное общество: идеи, технологии, системы» - Ч. 3 – Таганрог: ТТИ ЮФУ, 2010. – с. 4-8
13. Hosea M. E., Shampine L. F. “Analysis and implementation of TR-BDF2”, Applied Numerical Mathematics, vol. 20, No 1-2, 1996, pp. 21–37.
14. Бирюков В. Н. «Использование формул дифференцирования назад в одношаговом методе второго порядка точности», Математическое моделирование, 2009, т.21, № 11, с. 12-18.
15. Ракитский Ю. В., Устинов С. М., Черноруцкий И. Г. Численные методы решения жестких систем. М.: Наука, 1979, 208 с.
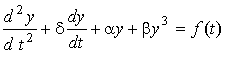
 б
б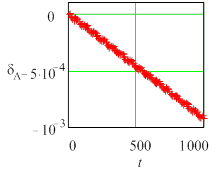 в
в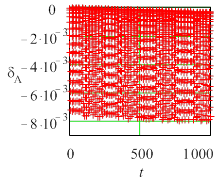 а
а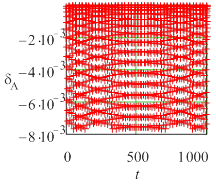 б
б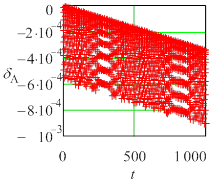
 а
а б
б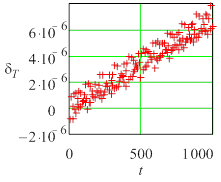 в
в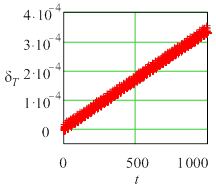 а
а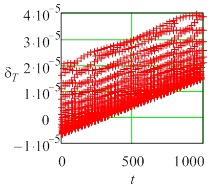 б
б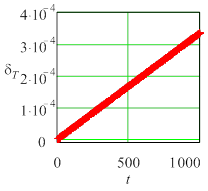 в
в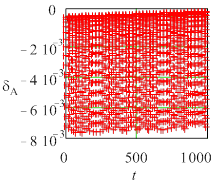
 б
б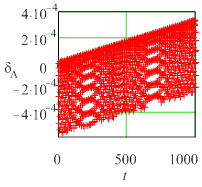 в
в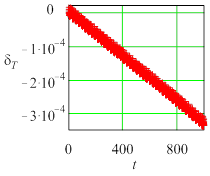 а
а б
б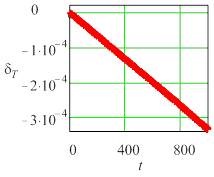 в
в