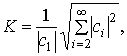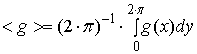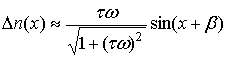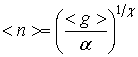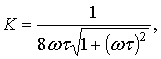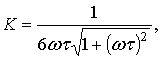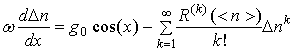УДК 621.383.4, 621.382.2/.3

НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ, ВОЗНИКАЮЩИЕ ПРИ ВОССТАНОВЛЕНИИ ВЫСОКОЧАСТОТНЫХ ОПТИЧЕСКИХ ИМПУЛЬСОВ

Е. В. Никишин, Е. Е. Пескова

Мордовский государственный университет им. Н.П. Огарева, г. Саранск

Статья получена 14 июля 2015 г.

Аннотация. В статье проведены теоретические исследования коэффициента нелинейных искажений восстановленного высокочастотного оптического сигнала. Расчеты сделаны для фотоприемников с различными законами рекомбинации. Определены условия, при которых нелинейных искажения малы.

Ключевые слова: механизмы рекомбинации, кинетика фотопроводимости, нелинейные искажения, периодическое возбуждение.

Abstract. In the article theoretical study of the nonlinear distortion of the restored high frequency optical signal. Calculations are made for photodetectors with different laws of recombination. The conditions under which nonlinear distortion is small.

Keywords: recombination mechanisms, kinetics of photoconductivity, nonlinear distortion, periodic excitation.

 

Введение

При регистрации оптического сигнала фотоприемниками возникают различного рода искажения, что ограничивает частотный диапазон датчиков при их использовании для получения зависимости интенсивности возбуждающего излучения () от времени. При малых частотах периодического внешнего возбуждения (квазистационарный режим)  зависимости  и зависимости концентраций неравновесных носителей (КНН) заряда от времени (,), следовательно, и проводимости от времени () представляются функциями, совпадающими с точность до постоянной величины.

При больших частотах возбуждения электрический и оптический импульсы не совпадают. В работах [1–3] изложен способ получения функции  по функции электропроводности фоторезистора. Используя операцию дифференцирования  можно найти зависимость интенсивности и скорости генерации носителей заряда от времени. Предложенный способ позволяет значительно расширить область частот, в которой возможно восстановление оптических импульсов. Методика восстановления серии импульсов реализуется, если их средняя длительность сравнима или меньше времени жизни основных носителей заряда (или ). То есть частота оптических сигналов должна быть больше граничной частоты фотодетектора. Кинетика фотопроводимости в этом случае практически не зависит от времен жизни электронов  и дырок и определяется, в основном, зависимостью величины темпа генерации от времени (или интенсивности).

Использование предложенного способа восстановления оптического сигнала приводит к возникновению частотных, фазовых и нелинейных искажений [4]. Нелинейные искажения вызваны нелинейностью процессов при обработке и передаче сигнала. Эти искажения вызывают появление в частотном спектре выходного сигнала отсутствующих во входном сигнале составляющих с частотами, кратными основной частоте (гармоники).  Степень  искажений характеризуется коэффициентом нелинейных искажений (КНИ). Под КНИ подразумеваем  величину равную отношению среднеквадратичного суммы гармоник интенсивности восстановленного сигнала, кроме первой, к величине первой гармоники интенсивности при возбуждении фотоприемника светом, переменная составляющая интенсивности которого изменяется по гармоническому закону () [4]:

 

                                                            (1)

здесь

.               

 

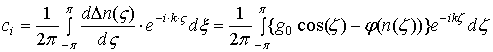Возникновение КНИ в первую очередь связано с нелинейностью законов рекомбинации. Цель работы: исследование нелинейных искажений, возникающих в зависимостях интенсивности падающего света от времени, восстановленных по зависимостям проводимости от времени, получаемым фотоприемниками с различными законами рекомбинации неравновесных носителей заряда.

Нелинейные искажения, возникающие при использовании фоторезисторов, изготовленных на основе кремния

В общем случае механизмы рекомбинации в кремнии достаточно сложны [5 - 9]. При расчетах КНН следует учитывать: рекомбинацию Шокли – Рида, межзонную рекомбинацию, межзонную Оже – рекомбинацию, безызлучательная экситонную рекомбинацию. Система дифференциальных уравнений, позволяющая рассчитать зависимости n(t), p(t), затем σ(t) имеет вид [4]:

,                                                 (2)

                                                 (3)

                    (4)

здесь: и  – численно равны концентрации электронов и дырок, когда уровень Ферми совпадает с уровнем ловушки j  типа; и – вероятности захвата электронов и дырок центрами  j  типа;  – вероятность нахождения электрона на центре  j  типа;  и– скорости рекомбинации электронов и дырок соответственно.

Темп межзонной генерации носителей заряда связан с интенсивностью (β - квантовый выход; k и R - коэффициенты поглощения и отражения света). Частота ω может изменяться со временем. Метод восстановления применим при условии . Темп рекомбинации электронов и дырок при наличии указанных выше механизмах:

, (5)

 (6)

 

Для получения переменной составляющей интенсивности света использовались соотношения:

,                (7)

Здесь

 ,   ,                                      

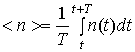С, С₁ – постоянные величины, зависящие от параметров полупроводника;  – подвижности электронов и дырок. Веденные выше величины  и  интерпретируются как средние значения концентрации электронов и дырок, около которых совершают колебания переменные составляющие КНН и .

Ниже приведены зависимости КНИ функции  для фоторезистора, изготовленного из кремния легированного индием. Индий формирует акцепторный уровень (E_v + 0.156 эВ; (0/+)) [5].   На рис. 1 представлены зависимости КНИ от частоты при различных значениях концентраций рекомбинационных центров индия. Принято считать, что при K<0,03 нелинейными искажениями можно пренебречь. Для нашего случая это означает, что восстановленный импульс практически не отличается от возбуждающего. Изменение концентрации рекомбинационных центров слабо изменяет величину КНИ.

Малые значения КНИ связаны с линеаризацией дифференциальных уравнений, описывающих зависимости концентраций электронов, дырок и вероятность нахождения электрона на рекомбинационном центре индия, которая возможна при возбуждении полупроводника импульсами света, интенсивность которых меняется с большой частотой. 

 

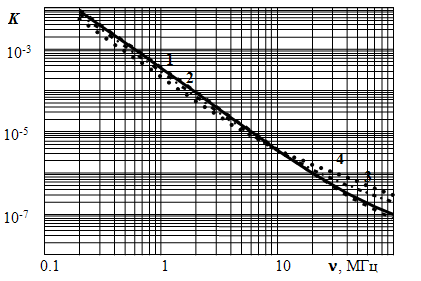
Рис. 1. Зависимости коэффициента нелинейных искажений от концентрации рекомбинационных центров  при  Q = 10²⁰ см^-3с^-1, n₀ = 10¹¹см^-3: 

1 – N_а = 10¹⁷ см^-3; 2 – N_а = 8∙10¹⁶ см^-3; 3 – N_а = 4∙10¹⁶см^-3, 4 – N_а = 2∙10¹⁶см^-3.

 

На рис. 2 представлены рассчитанные численными методами зависимости КНИ от частоты при различных значениях темпа генерации КНН. Расчеты проведены для фоторезистора, изготовленного из кристаллического кремния, легированного золотом. Золото в кремнии является амфотерной примесью. При рекомбинации через глубокие центры возникает необходимость учитывать их разные зарядовые состояния и разную глубину залегания в запрещенной зоне, что усложняет уравнения 5 и 6. Золото формирует донорный (E_v + 0.35 эВ; (0/+))  и акцепторный (E_c  – 0.55 эВ; (–/0)) глубокие уровни [10], причем в кремнии n-типа за эти уровни отвечают разные центры. Увеличение темпа генерации приводит к увеличению КНИ. Однако ввиду их малости в области частот, где выполняется неравенство влиянием  нелинейных искажений на искажения восстановленных импульсов можно пренебречь. Зависимости  имеют  экстремумы. Механизмы их возникновения достаточно сложны. В рассматриваемом случае . В области, где , искажения связаны с переменной составляющей концентрации избыточных электронов (), которая существенно превышает концентрацию переменной составляющей дырок (). Частота, при которой наблюдаются экстремумы, по порядку величины сравнима с обратной величиной времени жизни дырок (). В этой области вклад дырок в образование КНИ увеличивается. При  справедливо нестрогое равенство . Так как при этом  , то нелинейные искажения, обусловленные как электронами, так и дырками, становятся малыми. 

 

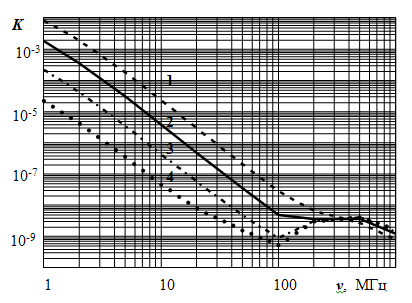
Рис. 2. Зависимости коэффициента нелинейных искажений от скорости генерации при N_а = 10¹⁵ см^-3, N_д = 10¹⁴ см^-3 n₀ = 10¹¹см^-3: 

1 – Q = 10²⁰ см^-3с^-1;   2 – Q = 10¹⁹ см^-3с^-1; 3 – Q = 10¹⁸см^-3с^-1; 4 – Q = 10¹⁷ см^-3с^-1.

 

Влияние закона рекомбинации на нелинейные искажения

Проведем анализ КНИ для наиболее часто встречающихся законов рекомбинации, которыми моделируются кинетические процессы. Для определенности рассмотрим полупроводник n-типа. Исследуем уравнение [6, 9]:

,                                                  (8)

Аналогичное уравнение справедливо для полупроводника p-типа.

Введем обозначения:

,    ,  ,  . (9)

 

Тогда вместо (8) имеем:

 .                         (10)

Пусть возбуждение осуществляется по закону

,     .                                       (11)

Рассмотрим полупроводник, у которого скорость рекомбинации основных носителей заряда (например, электронов), описывается степенной функцией:

,                                                          (12)

здесь  Подобная аппроксимация применима в частности при межзонной и Оже - рекомбинации, часто возможно ее использование при рекомбинации Шокли - Рида. В этом случае в области больших частот () уравнение (10) линеаризуется. Это приводит к тому, что с хорошей точностью кинетика переменной составляющей неравновесных носителей заряда  описывается линейным законом рекомбинации. Решение уравнения (10) в этом случае имеет вид:

  ,    ,   .     (13)

 

 Для средних значений концентрации электронов и времени их жизни, соответствующим заданному уровню возбуждения, справедливы соотношения:

 ,    .                    (14)

 

В области больших частот времена жизни ( и ), характеризующие соответственно рекомбинацию постоянной  и переменной  составляющей КНН отличаются друг от друга:

.                                   (15)

Ниже приведены соотношения для КНИ, при наиболее распространенных законах рекомбинации.

При квадратичном законе рекомбинации справедливы равенства:

, , , ,

,

.

 

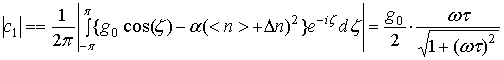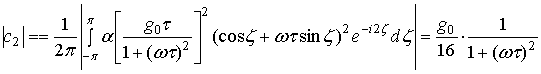При   

Для КНИ получаем:

                                                 (16)

При кубическом законе рекомбинации справедливы равенства:

, , ,,  ,

.

 

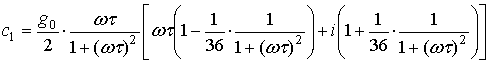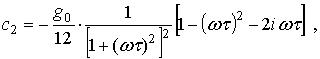
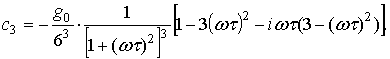При    Используя соотношение (1)  и значения коэффициентов , нетрудно получить КНИ при кубическом законе рекомбинации. В результате получается громоздкое выражение. Вместо него при выполнении неравенства удобно использовать соотношение:

                                              (17)

При произвольном законе рекомбинации используем разложение функции скорости генерации в ряд Тейлора  в окрестности концентрации , определяемой соотношением :

.                                     (18)

 

Уравнение (10) примет вид:

 ,                                       (19)

 

При исследовании нелинейных искажений ограничимся членами разложения с k =1, 2, 3. Коэффициенты разложения восстановленного сигнала в ряд Фурье:

   

 

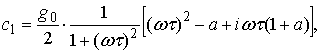
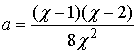
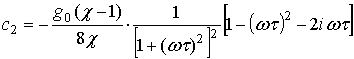
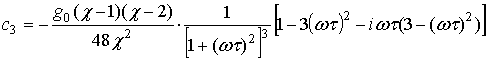
При  Используя соотношение (1) и полученные коэффициенты нетрудно получить КНИ при произвольном законе рекомбинации. Ввиду его громоздкости при выполнении неравенства можно использовать соотношение:

                                            (20)

На рис. 3 представлены зависимости КНИ от частоты изменения интенсивности оптического сигнала. Кривые 1 – 3 получены путем численного решения уравнения (8) при различных  законах рекомбинации. Затем, используя функции  для различных частот, по формуле 1 рассчитывались зависимости КНИ от частоты. Кривые 4 – 6  получены по соотношениям (16), (17), (20). Коэффициент α, входящий в закон рекомбинации (12) подбирался таким, чтобы время жизни электронов при разных значениях  оставалось одним и тем же и равным τ_n=10^-6 c. В области частот, удовлетворяющих условию , наблюдается хорошее их количественное согласие. При линейном законе рекомбинации  нелинейных искажений не возникает. Использование полученных соотношений позволяет достаточно легко оценивать КНИ.

 

Рис. 3. Зависимость КНИ от частоты: 1,4 –  , 2,5 –  , 3,6  –

 

Выводы

Исследованы нелинейные искажения, возникающие при применении способа восстановления оптических импульсов при помощи фоторезистора. Используемый способ на несколько порядков расширяет частотную область изменения интенсивности, в которой возможно восстановление. Анализ с использованием реальных значений параметров кристаллического кремния, легированного индием или золотом, показывает, что нелинейными искажениями в предложенном способе можно пренебречь. Ввиду сложности методики расчета КНИ предложены соотношения, позволяющие с хорошей точностью оценить КНИ по известным законам рекомбинации носителей заряда.  

 

Литература

1. Мхитарян В. М., Партамян Х. В. Скоростные фотоприемники импульсного излучения на основе «инерционных» фоторезисторов и фотодиодов.// ЖТФ,  1982, т. 52,  № 9, с. 1900 – 1902.

2. Горюнов В.А.,  Гришаев В.Я., Никишин Е.В. Кинетика фотопроводимости при возбуждении высокочастотными импульсами.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки,  2012,  №4, с. 242 – 250.

3. Гришаев В.Я., Никишин Е.В. Фотоэлектрический преобразователь высокочастотного оптического сигнала.//патент на полезную модель, RUS 132287, 24.12.2012.

4. Никишин Е.В. О границах применимости способа восстановления временной формы модулированных оптических сигналов с частотой выше граничной частоты фоторезистора.//Физика и техника полупроводников, 2014, т. 48, № 11, с. 1526-1529.        

5. Милнс А. Примеси с глубокими уровнями в полупроводниках.  М.: Мир, 1977. – 568 с.

6. Блекмор Д. Статистика электронов в полупроводниках.  М.: Мир, 1964. – 392 с.

7. Горюнов В.А.,  Гришаев В.Я., Никишин Е.В. Об изменении времен жизни носителей заряда при импульсном фотовозбуждении в кремнии с глубокими примесными центрами.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки, 2011, №4, с. 118-126

8. Denisov B. N., Nikishin E.V. Investigations of the Kinetics of Nonequilibrium Carriers in a Semiconductor by the Average Value of the Photoconductivity under Periodic Optical Excitation. // Semiconductors, 2014,  vol. 48, №2,  p.163-166.

9.  Смит Р. Полупроводники: пер. с англ.  М.: Мир, 1982. – 560 с.

10. D.V. Lang, H.G. Grimmeiss, E. Meijer, and M. Jaros, Complex nature of gold-related deep levels in silicon, Phys. Rev., 1980,  v. 22, p. 3917 – 3925.