| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11, 2001 |  |
ИССЛЕДОВАНИЕ ВЛИЯНИЯ ИМПЕДАНСНЫХ СВОЙСТВ ПЛОСКОСТИ
НА ПОЛЕ ИЗЛУЧЕНИЯ КРЕСТООБРАЗНЫХ ВИБРАТОРОВ
М. Ю.
Звездина
Ростовский военный институт ракетных войск
Получена 7 декабря 2001 г.
Приводятся соотношения и результаты исследований влияния импедансных свойств плоскости на структуру электромагнитного поля крестообразного электрического вибратора и крестообразного щелевого излучателя для различных способов реализации импедансных граничных условий.
Одним из важных вопросов, возникающих при разработке малоэлементных антенн с круговой поляризацией сигналов для станций спутниковой связи с объектами, находящимися на низких и средних орбитах, является обеспечение коэффициента эллиптичности не ниже 0.7 в широком секторе сканирования. Применение импедансных структур, наносимых на поверхность несущей конструкции вблизи излучающего раскрыва антенны, позволяет управлять структурой электромагнитного поля антенны [1-7].
Аппроксимация несущей конструкции импедансной плоскостью, а излучающих элементов антенн с круговой поляризацией сигналов – крестообразными электрическими вибраторами и крестообразными щелевыми излучателями, позволяет охватить достаточно широкий круг возможных конструкций малоэлементных антенн станций спутниковой связи. Исследованию влияния импедансных свойств поверхности тела на структуру электромагнитного поля расположенного вблизи него излучателя посвящено достаточное число работ, например, [3-15]. Однако вопрос влияния импедансной плоскости на характеристики направленности крестообразного электрического вибратора и крестообразного щелевого излучателя (крестообразного магнитного вибратора) рассмотрен недостаточно полно.
Решение задачи дифракции электромагнитной волны на импедансной плоскости будем осуществлять методом поверхностных граничных условий [9-12, 16], позволяющим моделировать электродинамические и геометрические свойства поверхности с помощью эквивалентного поверхностного импеданса. Соответствующая запись соотношений между напряженностями электрического и магнитного полей на границе поверхности имеет вид [16]:
где
![]() ‑
вектор нормали в границе раздела сред;
‑
вектор нормали в границе раздела сред; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ‑ диадические функции Грина,
определяющие поле
‑ диадические функции Грина,
определяющие поле ![]() или поле
или поле ![]() в точке
в точке ![]() для данного типа
источника (e –
электрического или m – магнитного типа), помещенного в точку
для данного типа
источника (e –
электрического или m – магнитного типа), помещенного в точку ![]() . При
вычислении выражений (1), (2) точка наблюдения
. При
вычислении выражений (1), (2) точка наблюдения ![]() полагается лежащей на
поверхности границы раздела сред. Диадические функции Грина могут быть найдены
с использованием выражений [15]:
полагается лежащей на
поверхности границы раздела сред. Диадические функции Грина могут быть найдены
с использованием выражений [15]:
где
![]() ‑
мнимая единица;
‑
мнимая единица; ![]() Ом – волновое сопротивление свободного
пространства;
Ом – волновое сопротивление свободного
пространства; ![]() ‑ волновое число свободного
пространства;
‑ волновое число свободного
пространства; ![]() ‑ длина волны; G
– функция Грина свободного пространства.
‑ длина волны; G
– функция Грина свободного пространства.
Использование интегрального преобразование Фурье в комплексной плоскости позволяет представить рассеянное импедансной плоскостью поле в виде непрерывного и дискретного спектров волн [8-16]. Причем непрерывный спектр волн описывает поле излучения, а дискретный – поле поверхностных волн. Асимптотическая оценка интегралы, выполненная для дальней зоны, дает возможность записать характеристики излучения рассматриваемых структур в следующем виде:
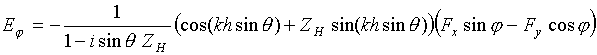 (7б)
(7б)
для крестообразного электрического вибратора и
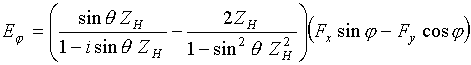 (8б)
(8б)
для крестообразного магнитного излучателя.
В
соотношениях (7), (8) ![]() ‑ соответственно диаграммы
x- и y- ориентированных
плеч крестообразного излучателя в свободном пространстве, описываемые соотношениями
[17]:
‑ соответственно диаграммы
x- и y- ориентированных
плеч крестообразного излучателя в свободном пространстве, описываемые соотношениями
[17]:
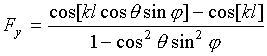 .
(9б)
.
(9б)
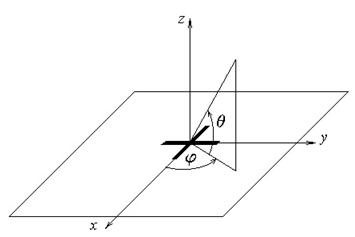
Вид излучающих элементов, размещение на несущей конструкции и отсчет углов показаны на рис.1а,б.
В
зависимости от способа реализации импедансных граничных условий на плоской
поверхности (нанесением слоя магнитодиэлектрика на металлическую поверхность
или применением ребристых структур (гофр), заполненных магнитодиэлектрическим
материалом) выражения для нормированного значения поверхностного импеданса ![]() имеют вид [1,
9-11, 16]:
имеют вид [1,
9-11, 16]:
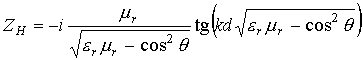 (10б)
(10б)
для магнитодиэлектрических структур и
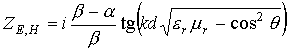 (10в)
(10в)
для ребристых структур.
В соотношениях (10) ![]() ‑
соответственно относительные диэлектрическая и магнитная проницаемости
магнитодиэлектрика;
‑
соответственно относительные диэлектрическая и магнитная проницаемости
магнитодиэлектрика; ![]() ‑ толщина слоя магнитодиэлектрика или
глубина канавки;
‑ толщина слоя магнитодиэлектрика или
глубина канавки; ![]() ‑ период следования канавки;
‑ период следования канавки; ![]() ‑ ширина
канавки. Следует отметить, что для ребристых структур от нуля отлична только та
компонента тензора поверхностного импеданса, которая соответствует типу волны
возбуждения.
‑ ширина
канавки. Следует отметить, что для ребристых структур от нуля отлична только та
компонента тензора поверхностного импеданса, которая соответствует типу волны
возбуждения.
Коэффициент эллиптичности может быть вычислен по известным значениям компонент векторной диаграммы направленности [4]
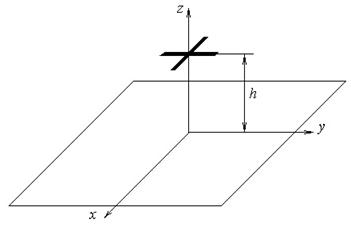
Анализ соотношений (7)-(10) показывает, что нанесение импедансных структур на плоскую поверхность изменяет структуру электромагнитного поля как крестообразного электрического вибратора, так и крестообразного щелевого излучателя. Помимо поля излучения в суммарном поле излучателя можно выделить поле поверхностных волн. Причем с ростом величины поверхностного импеданса вклад поверхностных волн в суммарное поле увеличивается, а поля излучения – уменьшается. Для крестообразных электрических вибраторов поле поверхностных волн зависит и от высоты подвеса излучателя над плоскостью. Изменяя высоту подвеса или величину поверхностного импеданса, можно управлять амплитудой поверхностных волн.
Несложно выявить зависимость компонент тензора поверхностного импеданса от угла прихода электромагнитной волны. Следует подчеркнуть, что при углах падения, близких к осевому, для получения более точных результатов необходимо использовать граничные условия более высокого, нежели первый, порядка [16].
На основе приведенных выше соотношений был разработан пакет программ, реализованных в языковой среде MathCad 7.0 pro, и проведены численные исследования характеристик излучения крестообразных электрического вибратора и крестообразного щелевого излучателя, расположенных в присутствии импедансной плоскости. Сравнение с данными, приведенными в [8-14], показали корректность разработанных программ.
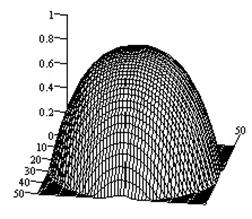
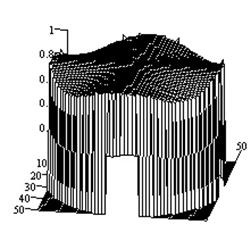
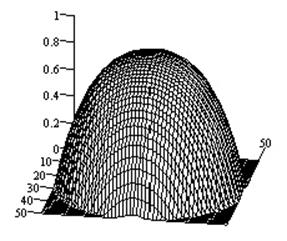
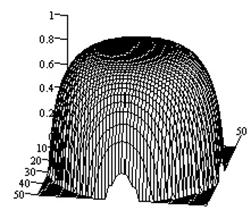
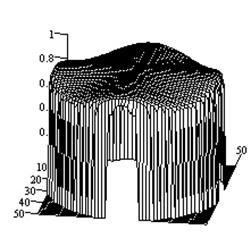
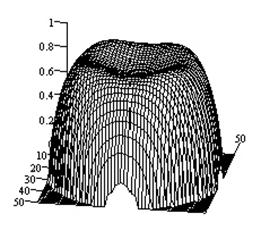
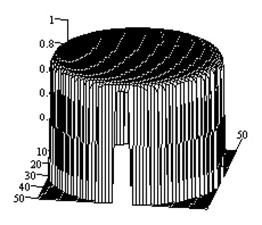
Рис.2-5
иллюстрируют результаты исследований влияния импедансных свойств плоскости на
характеристики направленности крестообразных излучателей. При этом на рис.2,
3
показаны характеристики направленности крестообразного электрического диполя с
моментом ![]() ,
расположенного на высоте
,
расположенного на высоте ![]() над идеально проводящей плоскостью и над
плоскостью с изотропным поверхностным импедансом
над идеально проводящей плоскостью и над
плоскостью с изотропным поверхностным импедансом ![]() соответственно. Рис.4,
5
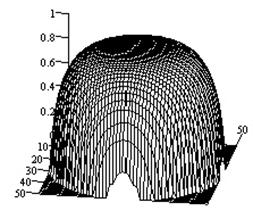
иллюстрируют характеристики направленности крестообразного щелевого излучателя
для тех же параметров импеданса.. Выбор изотропного поверхностного импеданса
определялся тем, что сканирование главного максимума ДН по углу азимута должно
проводиться в секторе
соответственно. Рис.4,
5
иллюстрируют характеристики направленности крестообразного щелевого излучателя
для тех же параметров импеданса.. Выбор изотропного поверхностного импеданса
определялся тем, что сканирование главного максимума ДН по углу азимута должно
проводиться в секторе ![]() .
.
Рисунки
с индексом "а" здесь и далее иллюстрируют поведение q-компоненты ДН в обобщенной системе координат ![]() ,
, ![]() , с индексом "б"
‑ j-компоненты векторной ДН; с индексом "в"
– поведение коэффициента эллиптичности.
, с индексом "б"
‑ j-компоненты векторной ДН; с индексом "в"
– поведение коэффициента эллиптичности.
Анализ
результатов исследований показывает, что влияние импедансной поверхности
незначительно влияет на характеристики направленности крестообразного
электрического вибратора. Для крестообразного щелевого излучателя данное
влияние проявляется в большей степени. Так, в направлении нормали происходит
снижение коэффициента эллиптичности с 1 (при размещении излучателя на идеально
проводящей поверхности) до 0.9 (при размещении на слое магнитодиэлектрика). В
то же время происходит расширение сектора, в котором коэффициент эллиптичности ![]() имеет величину
более 0.7. Так, если при размещении на идеально проводящей плоскости угловая ширина
сектора, в котором
имеет величину
более 0.7. Так, если при размещении на идеально проводящей плоскости угловая ширина
сектора, в котором ![]() , составляет
, составляет ![]() , то в случае импедансной поверхности
она достигает значения
, то в случае импедансной поверхности
она достигает значения ![]() . Диаграмма излучателя по мощности при этом
изменяется незначительно.
. Диаграмма излучателя по мощности при этом
изменяется незначительно.
Таким образом, использование импедансных поверхностей позволяет за счет возбуждения поверхностных и приповерхностных волн добиваться расширения пространственного сектора, в котором диаграмма направленности и коэффициент эллиптичности излучающего элемента имеют заданные параметры.
|
а |
б |
Рис.1. Геометрия задачи
|
а |
б |
в |
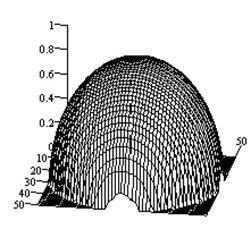
Рис.2.
Характеристики направленности крестообразного электрического вибратора над
идеально проводящей плоскостью (а - ![]() -компонента ДН; б
-
-компонента ДН; б
- ![]() -компонента
-компонента
ДН; в - объемный коэффициент эллиптичности).
|
а |
б |
в |
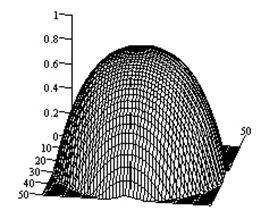
Рис.3.
Характеристики направленности крестообразного электрического вибратора над
плоскостью с изотропным импедансом ![]() (а -
(а - ![]() -компонента ДН; б
-
-компонента ДН; б
- ![]() -компонента
-компонента
ДН; в - объемный коэффициент эллиптичности).
|
а |
б |
в |
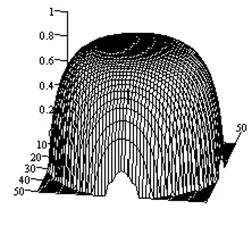
Рис.4.
Характеристики направленности крестообразного щелевого излучателя на идеально
проводящей плоскости (а - ![]() -компонента ДН; б
-
-компонента ДН; б
- ![]() -компонента ДН; в
- объемный коэффициент эллиптичности).
-компонента ДН; в
- объемный коэффициент эллиптичности).
|
а |
б |
в |
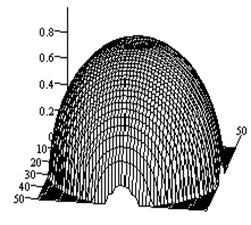
Рис.5.
Характеристики направленности крестообразного щелевого излучателя на плоскости
с изотропным импедансом ![]() (а -
(а - ![]() -компонента ДН; б
-
-компонента ДН; б
- ![]() -компонента ДН; в
- объемный коэффициент эллиптичности).
-компонента ДН; в
- объемный коэффициент эллиптичности).
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
-
Бененсон Л.С., Кюркчан А.Г. Метод развязки антенн при помощи периодических структур // Радиотехника. 1995. №12. С.62-69.
-
Скобелев С.П. Методы построения оптимальных фазированных антенных решеток для сканирования в ограниченном секторе // Электромагнитные волны и электронные системы. 1998. Т.3. №2. С.46-58.
-
Yoshitomi K. Polarization characteristics of radiation field from aperture in an impedance surface // IEEE Trans. Antennas and Propag. – 1996. – AP-44. №1. – Р.1464-1466.
-
Yoshitomi K. Radiation from a slot in an impedance surface // IEEE Trans. Antennas and Propag. – 2001. – AP-49. №10. – Р.1370-1376.
-
Звездина М.Ю. Управление уровнем бокового и заднего излучения антенн на основе применения импедансных структур // Журнал радиоэлектроники. 2001. №1. http://jre.cplire.ru/jre/jan01/2/text.html.
-
Габриэльян Д.Д.. Звездина М.Ю., Костенко П.И. Использование импедансных структур для улучшения электромагнитной совместимости / В сб. научн. докл IV Междунар. симпозиум «ЭМС-2001». Санкт-Петербург, 2001. С.368-371.
-
Габриэльян Д.Д., Звездина М.Ю., Костенко П.И. Влияние импедансной поверхности цилиндра на характеристики излучения // Журнал радиоэлектроники. 2000. №2. http://jre.cplire.ru/win/feb00/5/text.html.
-
Вайнштейн Л.А. Электромагнитные волны. – М.: Радио и связь, 1988. – 440 с.
-
Шевченко В.В. Плавные переходы в открытых волноводах. – М.: Наука, 1969. – 192с.
-
Каценеленбаум Б.З. Высокочастотная электродинамика. – М.: Наука, 1966. – 240 с.
-
Захарьев Л.Н., Леманский А.А., Щеглов К.С. Теория излучения поверхностных антенн. – М.: Сов. радио, 1969. – 232 с.
-
Бобровников М.С., Старовойтова Р.П., Смирнов В.П. Эффективность возбуждения поверхностных волн сосредоточенным источником на импедансной плоскости // Изв. вуз. Радиотехника. 1961. – Т.3. № 4. С.432-435.
-
Бобровников М.С., Смирнов В.П. Поле в ближней зоне источника при сосредоточенном возбуждении импедансной плоскости // Изв. вуз. Радиотехника. 1962. Т.4. №3. С.321-326.
-
Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. – М.: Радио и связь, 1983. – 296 с.
-
Васильев Е.Н. Возбуждение тел вращения. – М.: Радио и связь, 1983. – 384 с.
-
Cicchetti R., Faraone A. Exact surface impedance/admittance boundary conditions for complex geometries: Theory and applications // IEEE Trans. Antennas and Propag. – 2000. – AP-48. №3. – Р.223-230.
-
Айзенберг Г.З., Белоусов С.П.. Журбенко Э.М. и др. Коротковолновые антенн / Под ред. Г.З. Айзенберга. – М.: Радио и связь, 1985. – 536 с.
Автор:
Звездина Марина Юрьевна - кандидат технических наук, младший научный сотрудник РВИ РВ, zvezd@jeo.ru
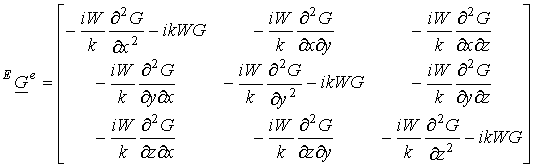 ,
(3)
,
(3)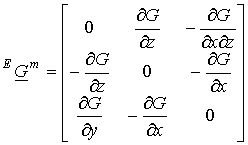 ,
(4)
,
(4)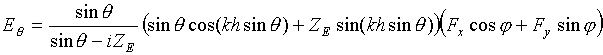 ,
, 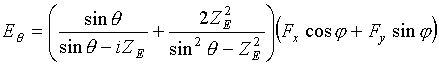 ,
, 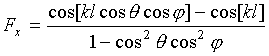 ,
(9а)
,
(9а)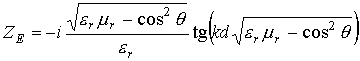 ,
(10а)
,
(10а)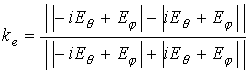 .
.