|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2002 |
|
СИНТЕЗ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ ПОТОКОМ КАДРОВ В СЕТЯХ GIGABIT ETHERNET
А. В. Макаренко, e-mail: compdep@nosu.ru
Северо-Кавказский государственный технологический университет
Получена 28 января 2002 г.
В работе разработана и исследована оптимальная по критерию качества обслуживания адаптивная система управления потоком кадров в сетях Gigabit Ethernet. Синтез системы управления проведен на основе положений технической кибернетики. Исследована устойчивость и оптимальность системы при значительных задержках управления, возникающих на протяженных каналах связи из-за конечной скорости распространения сигнала. С целью упрощения интерпретации результатов моделирования, рассмотрен только входной буфер порта коммутатора. По результатам анализа, показано, что синтезированная система управления на протяженных каналах связи обладает лучшими динамическими характеристиками нежели стандартная IEEE 802.3x.
1. ВВЕДЕНИЕ
2. СИНТЕЗ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ ПОТОКОМ КАДРОВ
3. ИССЛЕДОВАНИЕ СИНТЕЗИРОВАННОЙ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ ПОТОКОМ КАДРОВ
4. ВЫВОДЫ
5. ЛИТЕРАТУРА
В работе [1] была показана неоптимальность по критерию качества обслуживания [2] стандартной системы управления потоком кадров описанной в стандарте IEEE 802.3x [3] при задержках управляющего сигнала типичных для магистральных каналов связи. Одной из причин, объясняющих эту неоптимальность, является то обстоятельство, что стандарт был разработан для локальных сетей ориентированных в основном на передачу трафика данных. В тоже время опыт эксплуатации технологии Gigabit Ethernet показывает рост масштабов использования этой технологии в крупных сетях с новыми критичными приложениями, такими как передача компрессированного голоса, высококачественного видео, банковских транзакций, трафика Интернет [4], [5].
Исходя из вышесказанного, задача синтеза оптимальной системы управления потоком кадров при задержках управляющего сигнала является весьма актуальной.
Структура данной работы такова. В разделе 2, проводится синтез новой системы управления потоком кадров. В разделе 3, исследуется влияние задержки управляющего сигнала на устойчивость и оптимальность разработанной системы управления. В разделе 4, представлены выводы, и высказаны рекомендации по продолжению исследований в этом направлении.
2. СИНТЕЗ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ
ПОТОКОМ КАДРОВ
2.1. Постановка задачи
С позиций
технической кибернетики, математическая модель системы автоматического
управления (САУ) состоит из модели объекта управления (ОУ) и модели
устройства управления (УУ) [6]. При разработке модели ОУ
необходимо учесть, что объект управления состоит из двух частей: источника
трафика (ИТ) и устройства коммутации трафика (УКТ) при передачи сигнала
между которыми возможно наличие значительного транспортного запаздывания.
Нагрузкой коммутатора является потребитель трафика (ПТ). Структурная схема
системы представлена на рис. 2.1.
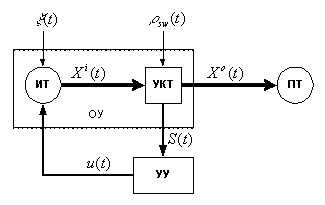
Рис. 2.1. Функциональная схема САУ потоком кадров
На источник
трафика, формирующий поток кадров описываемый вектором![]() воздействует
ненаблюдаемый вектор случайных возмущений
воздействует
ненаблюдаемый вектор случайных возмущений![]() с
неизвестной стохастичной структурой, и вектор управляющих воздействий
с
неизвестной стохастичной структурой, и вектор управляющих воздействий![]() .
Вектор управления формируется устройством управления, которое обрабатывает
.
Вектор управления формируется устройством управления, которое обрабатывает![]() –
вектор состояния устройства коммутации трафика, на которое воздействует
ненаблюдаемый вектор случайных возмущений
–
вектор состояния устройства коммутации трафика, на которое воздействует
ненаблюдаемый вектор случайных возмущений![]() с
неизвестной стохастичной структурой. Коммутатор генерирует поток кадров,
который описывается вектором состояния выходного канала
с
неизвестной стохастичной структурой. Коммутатор генерирует поток кадров,
который описывается вектором состояния выходного канала![]() .
.
Цель управления потоком, состоит в поддержке максимально возможной скорости следования кадров при гарантии отсутствия потерь из-за переполнения входного буфера, т.е.:
где![]() –
объем входного буфера,
–
объем входного буфера,![]() –
текущее значение очереди,
–
текущее значение очереди,![]() –
межкадровый интервал,
–
межкадровый интервал,
![]() –
переменная управления.
–
переменная управления.
При этом,
если значение управляющей переменной не превышает величины межкадрового
интервала, то на вход ОУ поступает истинное значение![]() ,
иначе на вход ОУ поступает значение
,
иначе на вход ОУ поступает значение![]() .
Начальным значением переменной управления является равенство
.
Начальным значением переменной управления является равенство
а ограничением неравенство
При цели управления в виде (2.1), система управления при соответствующем быстродействии, гарантирует защиту от переполнения входного буфера если соблюдается неравенство
где![]() –
граница эксплуатационной области входного буфера,
–
граница эксплуатационной области входного буфера,![]() ,
,
![]() –
задержка управления выраженная в количестве кадров находящихся в линии,
–
задержка управления выраженная в количестве кадров находящихся в линии,![]() –
длина кадра.
–
длина кадра.
Согласно принципам функционирования телекоммуникационных систем блок УУ должен выполнять следующие функции:
* управление коммутационным устройством;
* управление периодом поступления кадров.
Математическая модель динамики коммутатора Gigabit Ethernet (объекта управления) предложена в работе [7]. Модель учитывает переменный размер кадра, вариацию межкадровой паузы, и уровень загрузки коммутационного устройства. В ней учтены особенности режима коммутации с буферизацией («store-and-forwardЛ), так как именно этот режим применяется в большинстве магистральных коммутаторов Gigabit Ethernet. В работе [1] эта модель была расширена для учета ее активного управления потоком кадров. Следовательно для синтеза модели САУ требуется построить модель УУ.
Как уже отмечалось во введении, в работе [1] была показана неоптимальность по критерию качества существующей стандартной системы управления потоком кадров IEEE 802.3x. Там же был поставлен вопрос о необходимости синтеза оптимальной САУ потоком кадров нейтрализующей негативное влияние значительного транспортного запаздывания возникающего на магистральных каналах связи.
Оптимальность системы управления подразумевает ее адаптивность, ибо априорно известной информации зачастую бывает недостаточно для разработки оптимального на всем пространстве состояний закона управления [8]. Исходя из результатов полученных в работе [7] можно сделать вывод, что параметры задающие динамику объекта управления зависят как от входных, так и от возмущающих воздействий, которые по своей природе являются стохастичными. Вектор состояния объекта управления, как и вектор входных воздействий доступны наблюдению, но параметр определяющий задержку управляющего сигнала, стохастичен, наблюдению недоступен, и расчет его также невозможен.
Построение адаптивной системы управления на основе модели предсказания динамики очереди [8], не дает существенного выигрыша в качестве управления в силу того, что предсказание длины очереди с приемлемой точностью возможно лишь не более чем на 15 шагов.
Построение адаптивной системы управления на основе эталонной модели для точной работы требует применения двух моделей: модели входящего трафика и модели динамики коммутационного устройства. Модель динамики коммутатора дающая приемлемую точность создана и описана в работе [7], но удовлетворительной модели входящего трафика на сегодняшний день не существует.
Информационный трафик изначально моделировали на основе случайных последовательностей с заданными распределениями вероятностей. В частности, использовалась классическая модель с пуассоновским распределением и несколько моделей распределений с так называемыми «тяжелыми хвостамиЛ. Дальнейшее исследование статистических свойств информационных потоков показало, что трафик в телекоммуникационных системах является существенно нестационарным случайным процессом (как по своему среднему значению, так и по дисперсии) [9]. В настоящий момент в качестве близких к реальности математических моделей сложного трафика используются:
* марковски модулированный пуассоновский поток [10];
* самоподобные (фрактальные) случайные процессы [11];
* детерминистские процессы со странными аттракторами [10];
* нейронные сети [12].
Этим моделям присущи определенные недостатки, главный из которых – узкая специализация под конкретный вид трафика. В реальных мультисервисных телекоммуникационных сетях присутствует как минимум три вида трафика: видео, телефония и компьютерные данные. Каждый из этих видов характеризуется собственным, уникальным набором статистических параметров, что требует перестройки модели. Но от системы управления потоком кадров требуется малое время реакции, а все вышеперечисленные модели требует затрат значительного времени на вычислительные процедуры.
Вышеуказанные обстоятельства и определяют использование в разрабатываемой
САУ комбинации шаговых поисковых методов оптимизации с аналитической
самонастройкой по замкнутому циклу. Замкнутый цикл используется в силу того,
что вектор случайных возмущений![]() ненаблюдаем.
Аналитическая самонастройка должна производиться по внешним воздействиям и
динамическим характеристикам объекта управления [8].
Применение шаговых методов поисковой оптимизации объясняется тем, что
параметр определяющий задержку управляющего сигнала, стохастичен, наблюдению
недоступен, и расчет его также невозможен. Принимая во внимание
вышеизложенное, укрупненную структуру синтезируемого устройства управления
можно представить в следующем виде, рис. 2.2.
ненаблюдаем.
Аналитическая самонастройка должна производиться по внешним воздействиям и
динамическим характеристикам объекта управления [8].
Применение шаговых методов поисковой оптимизации объясняется тем, что
параметр определяющий задержку управляющего сигнала, стохастичен, наблюдению
недоступен, и расчет его также невозможен. Принимая во внимание
вышеизложенное, укрупненную структуру синтезируемого устройства управления
можно представить в следующем виде, рис. 2.2.
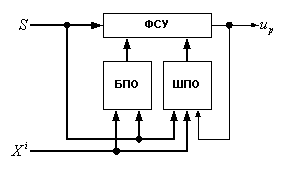
Рис. 2.2. Укрупненная блок-схема УУ
На рис. 2.2, обозначены: ФСУ – формирователь сигнала управления, БПО – беспоисковый оптимизатор, ШПО – шаговый поисковый оптимизатор.
Основное
назначение блока ФСУ – реализация закона управления и расчет значений
вектора управления![]() .
В БПО на основе измерения
.
В БПО на основе измерения![]() –
вектора входных воздействий и
–
вектора входных воздействий и![]() –
вектора состояния ОУ, производится подстройка параметров закона управления.
В ШПО ведется варьирование параметров закона управления, и ищется
экстремальное значение – минимум функционала качества управления
[1].
–
вектора состояния ОУ, производится подстройка параметров закона управления.
В ШПО ведется варьирование параметров закона управления, и ищется
экстремальное значение – минимум функционала качества управления
[1].
Прежде чем приступить собственно к синтезу структуры главного и адаптационных контуров управляющего устройства, кратко опишем модель объекта управления.
2.2. Описание математической модели ОУ
В качестве математической модели коммутатора (ОУ) используем модель разработанную и описанную в работе [7], и расширенную для учета ее активного управления потоком кадров в работе [1].
Если принять допущение об
однородности трафика, то каждое состояние канала![]() –
номер сгенерированного кадра, будет состоять из двух фаз: под первой фазой
понимается межкадровая пауза ("p-"), под второй фазой передача
кадра ("p+"). Длительность межкадрового интервала обозначим
–
номер сгенерированного кадра, будет состоять из двух фаз: под первой фазой
понимается межкадровая пауза ("p-"), под второй фазой передача
кадра ("p+"). Длительность межкадрового интервала обозначим![]() ,
а длительность передачи кадра
,
а длительность передачи кадра![]() .
Процесс передачи кадров показан на рис. 2.3.
.
Процесс передачи кадров показан на рис. 2.3.
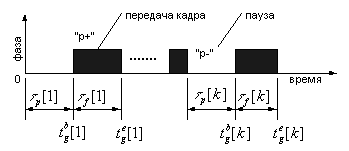
Рис. 2.3. Функциональная диаграмма
процесса передачи кадров в канале
Длительность фазы "p+" связана с размером
кадра![]() ,
соотношением
,
соотношением
где![]() –
битовая скорость канала, постоянный аппаратный параметр. Начало передачи
кадра
–
битовая скорость канала, постоянный аппаратный параметр. Начало передачи
кадра![]() характеризуется
временной отметкой
характеризуется
временной отметкой![]() ,
а окончание отметкой
,
а окончание отметкой![]() .
Технология Gigabit Ethernet передает кадры переменной длины при переменном
межкадровом интервале, поэтому минимальный вектор состояния канала
характеризуется двумя компонентами [14]:
.
Технология Gigabit Ethernet передает кадры переменной длины при переменном
межкадровом интервале, поэтому минимальный вектор состояния канала
характеризуется двумя компонентами [14]:
При необходимости, минимальный вектор состояния канала может быть расширен компонентами из заголовочной части кадра, а также переменными сетевого и транспортного уровней, содержащимися в поле полезной нагрузки.
Кадр Gigabit Ethernet состоит из преамбулы (служит для синхронизации передатчика и приемника физического уровня), служебной части и полезной нагрузки [14]. Размер преамбулы в дуплексном режиме зафиксирован в 64 бита, а служебной части в 144 бит. Минимальное значение «чистогоЛ межкадрового интервала в точности равно времени передачи 96 бит и составляет для Gigabit Ethernet 96 нс, а максимальное значение не ограниченно. Учитывая что преамбула на канальном уровне не обрабатывается, получаем значение «реальногоЛ минимального межкадрового интервала в 160 нс.
В итоге
получаем, что компонента![]() вектора
вектора![]() дискретна
по своей природе и определена на битовом отрезке
дискретна
по своей природе и определена на битовом отрезке
с дискретой в 8 бит. Компонента![]() непрерывна
и определена на наносекундном полуинтервале
непрерывна
и определена на наносекундном полуинтервале
С точностью
достаточной для инженерных расчетов, компоненту![]() можно
также представить дискретной, с интервалом дискретизации в 1нс. Ошибка
дискретизации в этом случае составляет не более
можно
также представить дискретной, с интервалом дискретизации в 1нс. Ошибка
дискретизации в этом случае составляет не более![]() .
Тогда процесс порождающий минимальный вектор состояния канала, будет
дискретен и по времени и по уровню.
.
Тогда процесс порождающий минимальный вектор состояния канала, будет
дискретен и по времени и по уровню.
Полная
структура модели ОУ изображена на рис. 2.4. На вход
коммутационного устройства от источника трафика (ИТ) поступает поток заявок,
который описывается двумя случайными величинами:![]() –
длительность межкадрового интервала, и
–
длительность межкадрового интервала, и![]() –
размер кадра. Битовая скорость коммутации
–
размер кадра. Битовая скорость коммутации![]() принимается
постоянной, так как является аппаратным параметром. Время обработки
принимается
постоянной, так как является аппаратным параметром. Время обработки![]() в
общем случае зависит от размера кадра, времени обработки заголовка
процессором
в
общем случае зависит от размера кадра, времени обработки заголовка
процессором![]() (производится
проверка контрольной суммы и определяется выходной порт по записи «адрес-портЛ
в таблице коммутации) и времени остающегося до освобождения выходного порта
занятого другими процессами
(производится
проверка контрольной суммы и определяется выходной порт по записи «адрес-портЛ
в таблице коммутации) и времени остающегося до освобождения выходного порта
занятого другими процессами![]() .
Две последние величины в нашей модели принимаем случайными, они зависят от
конкретной технической реализации коммутатора и от режима его
функционирования. Эти величины являются возмущением, приведенным к ОУ.
.
Две последние величины в нашей модели принимаем случайными, они зависят от
конкретной технической реализации коммутатора и от режима его
функционирования. Эти величины являются возмущением, приведенным к ОУ.
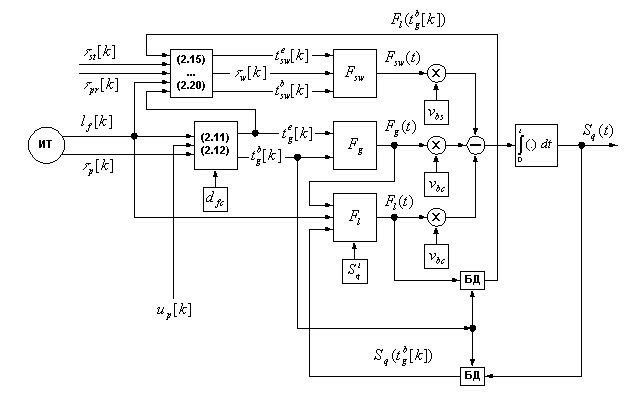
Рис. 2.4. Полная структура математической модели САУ
БД – обозначает дискретизацию функции по временной отметке.
Так как входной буфер коммутатора имеет ненулевую конечную емкость, то для коммутационного устройства справедлив «закон балансаЛ, выражающийся в равенстве количества поступивших в систему кадров сумме количеств скоммутированных, потерянных, и находящихся в буфере. Потерянные кадры возникают в силу конечной емкости буфера, при возникновении перегрузки и переполнении входного буфера. В качестве математической модели «закона балансаЛ, используем выражение
Функцию состояния источника трафика в терминах
непрерывного времени![]() выразим
следующим образом:
выразим
следующим образом:
где![]() –
функция Хевисайда.
–
функция Хевисайда.
Принимая во
внимание дискретность процесса генерации кадров, с учетом влияния на него
управляющей переменной![]() ,
моменты времени начала
,
моменты времени начала![]() и
окончания
и
окончания![]() фазы
"p+", выразим следующим образом:
фазы
"p+", выразим следующим образом:
где![]() –
номер обрабатывающегося кадра,
–
номер обрабатывающегося кадра,![]() ,
,![]() –
задержка управления выраженная в количестве кадров находящихся в линии.
–
задержка управления выраженная в количестве кадров находящихся в линии.
Именно
выражение (2.11) и учитывает управление потоком кадров.
При этом, если значение управляющей переменной не превышает величины
межкадрового интервала, то на вход ОУ поступает истинное значение![]() ,
иначе на вход ОУ поступает значение
,
иначе на вход ОУ поступает значение![]() .
.
Через
функцию![]() определяется
состояние коммутатора теряющего (сбрасывающего) входящие кадры из-за
переполнения его входного буфера емкостью
определяется
состояние коммутатора теряющего (сбрасывающего) входящие кадры из-за
переполнения его входного буфера емкостью![]() .
.
Принимая во внимание вышесказанное, функцию сброса кадров определим так:
Функцию состояния коммутационной матрицы![]() (функцию коммутации) в терминах непрерывного времени
(функцию коммутации) в терминах непрерывного времени![]() определим
так:
определим
так:
Учитывая особенности функционирования коммутатора в
режиме «store-and-forwardЛ и учитывая дискретность процесса коммутации
кадров, моменты времени начала![]() и
окончания
и
окончания![]() обработки
кадров выразим следующим образом:
обработки
кадров выразим следующим образом:
а время обработки через
Время собственно коммутации определяется размером кадра![]() и
битовой скоростью коммутации
и
битовой скоростью коммутации![]() .
Выразим
.
Выразим
Моменты времени начала и окончания собственно процесса коммутации кадра, выразим следующим образом:
В работе [7] показана адекватность модели реальному коммутатору «Cajun P550Л, производства компании «AvayaЛ, в части оценки его вероятностно-временных характеристик. Максимальная ошибка моделирования не превышает 10%, это говорит о достаточной адекватности модели исследуемому объекту. Данная точность вполне приемлема для практических, инженерных исследований.
2.3. Критерий оптимальности и функционал качества управления
Для адекватной оценки качества системы управления в технической кибернетике введены понятия критерия оптимальности и функционала качества управления [8]. Воспользуемся функционалом разработанным в работе [1], в которой исходя из смысла решаемой задачи, была выбрана форма функционала качества системы управления на основе функции Лагранжа:
где![]() –
оператор математического ожидания,
–
оператор математического ожидания,![]() –
номер кадра,
–
номер кадра,
![]() –
период оптимизации,
–
период оптимизации,![]() –
функция Лагранжа.
–
функция Лагранжа.
Функция Лагранжа состоит из двух слагаемых:
где![]() –
нормирующий коэффициент.
–
нормирующий коэффициент.
В выражении (2.22) в качестве слагаемого характеризующего затраты на управление, была выбрана стандартная квадратичная форма. При этом, если значение управляющей переменной не превышает величины межкадрового интервала, то управление не оказывает никакого влияния на процесс передачи кадров и затраты на управление равны нулю.
Функция штрафа![]() представляется
в виде:
представляется
в виде:
где![]() –
нормирующие коэффициенты,
–
нормирующие коэффициенты,
![]() –
параметр ограничивающий эксплуатационную область.
–
параметр ограничивающий эксплуатационную область.
Учитывая, что на вход объекта управления действует стохастический процесс, и оптимальность системы управления требуется в большом, период оптимизации в функционале (2.21) составляет весь период функционирования системы [13].
2.4. Разработка закона управления
Исходя из того, что целью системы управления потоком кадров (2.1) является защита входного буфера порта коммутатора от переполнения, представляется логичным, сделать переменную управления зависимой от длины очереди. За основу закона управления синтезируемой САУ, возьмем нелинейность с насыщением, характеристика которой изображена на рис. 2.5.
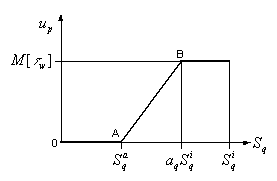
Рис. 2.5. Характеристика нелинейности с насыщением
Выбор данного вида нелинейности обусловлен ее
адекватностью физическому смыслу задачи управления. Немаловажным критерием
выбора вида закона управления является отсутствие у процессора порта,
математического сопроцессора. Ордината точки B, является точкой
динамического равновесия в которой скорость поступления данных равна
скорости их обработки, а абсцисса границей эксплуатационной зоны. Ордината
точки A равна нулю, а абсцисса является адаптируемым параметром![]() (рис.
2.5). При этом справедливы следующие ограничения:
(рис.
2.5). При этом справедливы следующие ограничения:
Принимая во внимание то, что
если значение управляющей переменной не превышает величины межкадрового
интервала, то на вход ОУ поступает истинное значение![]() ,
иначе на вход ОУ поступает значение
,
иначе на вход ОУ поступает значение![]() ,
модифицируем исходную нелинейность следующим образом, рис.
2.6. При этом отрезок AB описывается уравнением прямой проходящей через
две точки:
,
модифицируем исходную нелинейность следующим образом, рис.
2.6. При этом отрезок AB описывается уравнением прямой проходящей через
две точки:
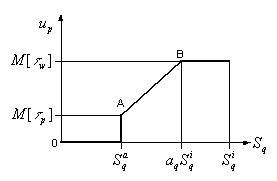
Рис. 2.6. Характеристика модифицированной
нелинейности с насыщением
Исходя из того, что чем выше значение математического
ожидания скорости роста очереди, тем более опасен для ОУ выход за границу
эксплуатационной области, модифицируем закон управления, введя
дополнительный «скачокЛ, рис. 2.7. Зависимость параметра![]() от
скорости изменения длины очереди определим следующим образом:
от
скорости изменения длины очереди определим следующим образом:
где![]() –
нормирующий коэффициент,
–
нормирующий коэффициент,![]() .
.
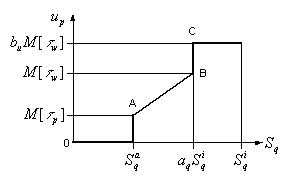
Рис. 2.7. Характеристика упрощенного закона управления
При этом справедливы следующие ограничения:
Для повышения устойчивости системы управления в целом, расширим закон управления, до гистерезисной нелинейности, введя обратную ветвь, рис. 2.8.
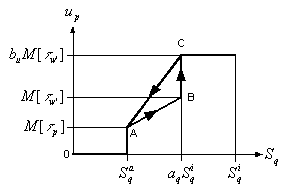
Рис. 2.8. Характеристика полного закона управления
Дополнительное повышение устойчивости системы
управления достигается за счет расчета![]() без
учета потерь кадров, для этого модифицируем выражение (2.17):
без
учета потерь кадров, для этого модифицируем выражение (2.17):
В итоге, полный закон управления представим выражениями
При этом, соотношение (2.29а)
описывает прямую ветвь, а (2.29б) обратную. Параметры
закона управления кроме![]() ,
адаптируются аналитически. Для нахождения параметра
,
адаптируются аналитически. Для нахождения параметра![]() ,
требуется поисковая оптимизация. Для оценки математического ожидания величин
,
требуется поисковая оптимизация. Для оценки математического ожидания величин![]() и
и![]() используем
скользящее среднее:
используем
скользящее среднее:
где![]() и
и![]() ширина
окон усреднения величин
ширина
окон усреднения величин![]() и
и![]() соответственно.
соответственно.
Если ширину окон усреднения выбрать «слишком большойЛ, то система управления будет отставать в реакции на изменения входящих воздействий и динамических характеристик ОУ, если ширина окон усреднения будет «слишком малойЛ, то в системе появится «высокочастотный дребезгЛ. Исходя из динамики очереди, предлагается следующая эмпирическая формула для расчета ширины окна усреднения:
Определить влияние параметров закона управления на качество управляющей системы можно решив прямую задачу теории чувствительности. Для этого по известным функциям чувствительности и величинам вариации параметров закона управления исследуются дополнительные движения выходного вектора объекта управления [15].
2.5. Разработка алгоритма адаптации закона управления
Идея экстремального регулирования как нового направления в развитии систем управления динамическими объектами впервые была выдвинута в СССР в 1943-1945 гг. [16], [17]. В этих работах был показан принцип действия систем экстремального регулирования (СЭР), разработаны методы решения задачи синтеза систем, проведено теоретическое исследование динамики распространенных технических объектов.
Поисковые
системы экстремального управления существенно отличаются от обычных систем
стабилизации. В поисковых СЭР отыскиваются некоторые заранее неизвестные
значения управляющих переменных![]() ,
соответствующие экстремуму определенного функционала
,
соответствующие экстремуму определенного функционала![]() ,
являющегося показателем цели управления, а не устраняется рассогласование
между управляющими воздействиями
,
являющегося показателем цели управления, а не устраняется рассогласование
между управляющими воздействиями![]() и
регулируемыми параметрами
и
регулируемыми параметрами![]() до
некоторых допустимых пределов ошибки, как в обычных системах управления.
Применение экстремальных систем управления не требует полной априорной
информации об объекте управления, и/или о процессах воздействующих на его
вход.
до
некоторых допустимых пределов ошибки, как в обычных системах управления.
Применение экстремальных систем управления не требует полной априорной
информации об объекте управления, и/или о процессах воздействующих на его
вход.
Основным в классификации экстремальных систем является их деление на типы по способам поиска экстремума:
* с запоминанием экстремума;
* с измерением производной;
* шагового типа;
* непрерывного действия с модулирующими воздействиями.
Экстремальные системы можно оценить по их
помехоустойчивости и по качеству регулирования. К показателям качества
относят время поиска экстремума (быстродействие), «потери на рысканьеЛ, а
также значения амплитуд колебаний на входе в объект управления и на его
выходе. В настоящей работе методы поискового экстремального управления
применяются для поиска значения параметра![]() закона
управления (2.29).
закона
управления (2.29).
Учитывая, что сигнал на входе объекта управления стохастичный и в системе потенциально возможно значительное транспортное запаздывание, в качестве алгоритма поиска экстремума применим метод шагового поиска. Критерий выбора – максимальное быстродействие и устойчивость поиска, минимальное рысканье.
В экстремальных системах шагового типа, величина шага может быть постоянной или переменной, в частности пропорциональной значению производной экстремума, или пропорциональной интервалу поиска.
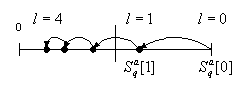
В настоящей работе используется известный аналог дихотомии – поиск по «золотому сечениюЛ [18], при этом интервал поиска разбивается на два отрезка в соотношении 1:1,618. рис. 2.9 иллюстрирует этот метод. При применении метода «золотого сеченияЛ возможны два режима поиска:
*
нормальный,![]() ,
рис. 2.9а;
,
рис. 2.9а;
*
форсированный,![]() ,
рис. 2.9б.
,
рис. 2.9б.
Под![]() понимается
номер шага поиска при оптимизации закона управления.
понимается
номер шага поиска при оптимизации закона управления.
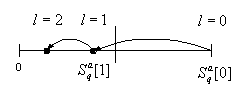
а)
б)
Рис. 2.9. Иллюстрация метода золотого сечения при поиске
экстремума
Для каждого режима, возможны два направления поиска:
*
влево, с уменьшением варьируемого параметра,![]() ;
;
*
вправо, с увеличением варьируемого параметра,![]() .
.
На процесс поиска наложено следующее начальное значение направления поиска:
Закон, по которому варьируется параметр![]() представим
в виде:
представим
в виде:
где![]() –
параметр определяющий малый отрезок «золотого сеченияЛ, а
–
параметр определяющий малый отрезок «золотого сеченияЛ, а![]() –
больший отрезок «золотого сеченияЛ.
–
больший отрезок «золотого сеченияЛ.
Структурная схема ШПО приведена на рис. 2.10, где: БРФ – блок расчета функционала, БАН – блок адаптации и настройки.
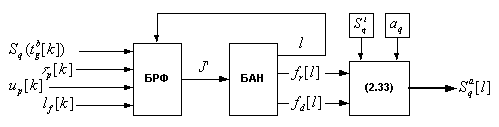
Рис. 2.10. Структурная схема ШПО
В БРФ производится вычисление функционала качества управления, а БАН управляет процессами расчета функционала и поиска оптимального параметра закона управления.
Для применения в БРФ, функционал (2.21) несколько модифицируем:
где![]() –
интервал оптимизации,
–
интервал оптимизации,![]() –
номер шага поиска ,
–
номер шага поиска ,![]() –
модифицированная функция Лагранжа.
–
модифицированная функция Лагранжа.
Модификация функционала (2.21) заключается в изменении интервала оптимизации для возможности проведения шагового поиска и изменении функции Лагранжа.
Модификация
функции Лагранжа связана с ненаблюдаемостью в реальной ситуации истинного
межкадрового интервала![]() при
ненулевом значении управляющей переменной
при
ненулевом значении управляющей переменной![]() .
Модифицированная функция имеет следующий вид:
.
Модифицированная функция имеет следующий вид:
где![]() –
нормирующий коэффициент,
–
нормирующий коэффициент,![]() –
функция штрафа.
–
функция штрафа.
Алгоритм, которым
управляется поиск реализован в БАН, и основан на дискретном процессе расчета
значений функционала качества управления (2.35). Его
значения подаются на запоминающее устройство, которое подает на элемент
сравнения (ЭС) предыдущее значение функционала. На ЭС одновременно поступает
текущее значение функционала. На выходе ЭС получается сигнал разности. Если![]() ,
то такое изменение параметров закона управления допускается, и оптимизация
идет в заданном направлении
,
то такое изменение параметров закона управления допускается, и оптимизация
идет в заданном направлении
Если же![]() ,
то параметр закона управления
,
то параметр закона управления![]() оптимизируется в обратном направлении
оптимизируется в обратном направлении
На выходе ЭС включен еще один элемент, который управляет шагами оптимизации.
В связи с
тем, что в основе действия системы экстремального управления – поисковые
движения, а априорная информация является неполной, вопросы устойчивости
стоят более остро, чем в обычных системах стабилизации. Исходя из данных
полученных при исследовании динамики объекта управления можно вполне
допустить наличие вертикального дрейфа экстремума, при котором система
экстремального управления теряет устойчивость [19].
Эффективным способом уменьшения уходов системы и увеличения ее устойчивости,
является введение коммутатора поверочных реверсов – устройства, периодически
и принудительно реверсирующего направление поиска [20],
при этом применяется выражение (2.36б). При этом
целесообразно, что бы период реверсирования![]() отсчитывался
от момента времени реверса вызванного действием ЭС. Также возможно на момент
принудительного реверсирования переходить в режим форсированного поиска
[18].
отсчитывался
от момента времени реверса вызванного действием ЭС. Также возможно на момент
принудительного реверсирования переходить в режим форсированного поиска
[18].
Полная структурная схема синтезированной адаптивной системы автоматического управления (AFC) потоком кадров приведена на рис. 2.11, где линиями увеличенной толщины выделен основной контур управления.
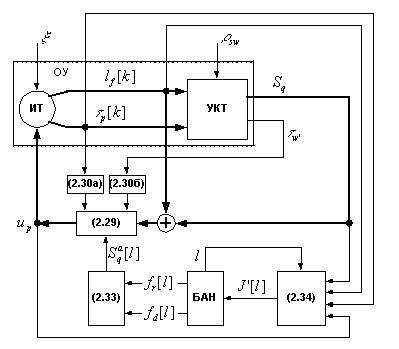
Рис. 2.11. Блок-схема синтезированной САУ
3. ИССЛЕДОВАНИЕ СИНТЕЗИРОВАННОЙ АДАПТИВНОЙ
СИСТЕМЫ УПРАВЛЕНИЯ ПОТОКОМ КАДРОВ
3.1. Постановка задачи
Согласно положениям МСЭ-Т [2], качество обслуживания улучшается, когда значения параметров: вероятность потери кадра, задержка и вариация задержки при передачи кадра достигают своего минимума. Следовательно, основными динамическими характеристиками коммутирующих устройств, задающими качество обслуживания, являются следующие величины:
![]() –
текущая длина очереди [бит];
–
текущая длина очереди [бит];
где![]() –
вероятность потери кадра из-за переполнения входного буфера;
–
вероятность потери кадра из-за переполнения входного буфера;
где![]() –
величина задержки при коммутации кадра [сек];
–
величина задержки при коммутации кадра [сек];
где![]() –
отклонение в задержках соседних кадров (Джиттер) [сек];
–
отклонение в задержках соседних кадров (Джиттер) [сек];
где![]() –
рост межкадрового интервала [сек].
–
рост межкадрового интервала [сек].
Принимая во внимание результаты
работы [1], представляется целесообразным анализ влияния
задержки управления на качество синтезированной САУ провести по оценке
математического ожидания и максимальному значению следующих параметров:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
задающих качество обслуживания, и по параметрам
,
задающих качество обслуживания, и по параметрам![]() и
и![]() .
.
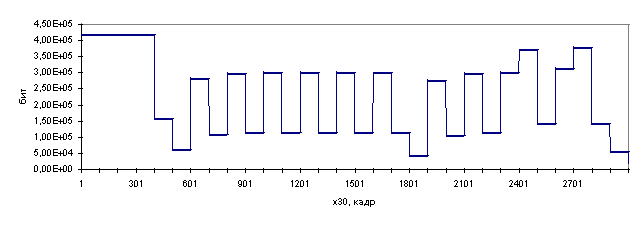
3.2. Результаты численного моделирования
Численное
моделирование стандартной системы управления проводилось при уровне загрузки
коммутатора в 0,5 – данная величина является типичной. На вход подавался
реальный трафик с длиной последовательности в 100 000 кадров и со средним
уровнем загрузки канала в 0,78. Объем буфера входного порта принимался
равным 256КБ, а порог срабатывания САУ был установлен в 51КБ. В
эксперименте использовались те же самые аппаратные параметры модели ОУ, что
и при оценке ее адекватности [7]. Данное обстоятельство
позволяет привязать результаты моделирования к коммутатору «Cajun P550Л, и
тем самым повысить практическую значимость результатов работы.
В табл. 3.1 приведены усредненные
показатели линий связи для каналов с типичной протяженностью. Диапазон
охватывает значения от локальных до глобальных сетей.
Усредненные показатели длинных линий
|
Длина канала, |
Задержка управления, |
Количество кадров в линии, |
Объем данных в линии, |
|
0,1 |
505 |
1 |
800 |
|
1 |
3 507 |
3 |
2 400 |
|
5 |
16 849 |
15 |
11 800 |
|
20 |
66 883 |
50 |
40 000 |
|
50 |
166 949 |
120 |
100 000 |
|
100 |
333 727 |
250 |
200 000 |
|
1 000 |
3 335 729 |
2 550 |
2 000 000 |
Функционал качества управления (2.21)
рассчитывался при следующих значениях нормирующих коэффициентов:![]() ,
,![]() ,
,![]() ,
параметр
,
параметр![]() [1].
[1].
В контуре
адаптивной настройки применялись следующие значения параметров:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
В данной работе не рассматривалось влияние алгоритмов управления классами, и очередями на динамику САУ, так как на поведение разработанной системы управления влияния они не оказывают.
На
рис. 3.1 приведены графики зависимости функционала оптимальности (2.21),
а на рис. 3.2 параметров динамики от задержки
управления. Рис. 3.3 иллюстрирует процесс поиска оптимального значения
параметра![]() при
различных значениях задержки управления.
при
различных значениях задержки управления.
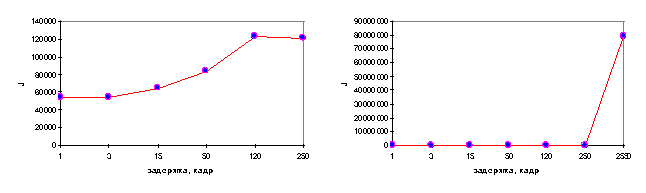
а)
б)
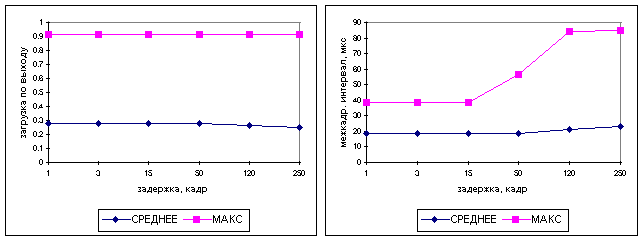
Рис. 3.1. Зависимость функционала оптимальности от задержки управления
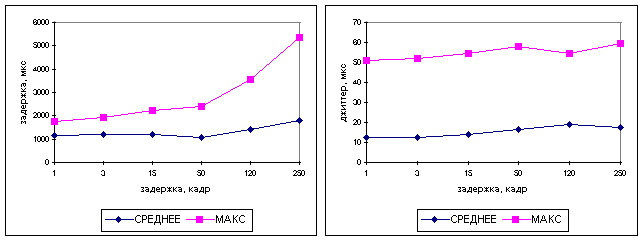
д)
е)
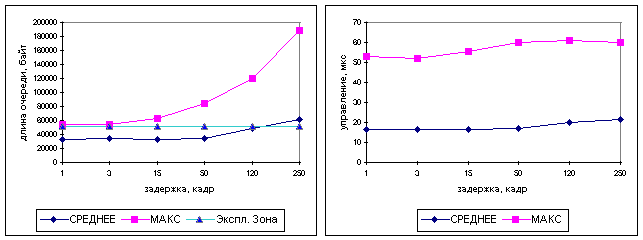
Рис. 3.2. Зависимость вероятностно-временных характеристик от
задержки управления
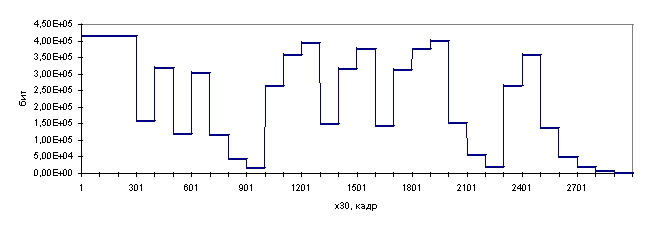
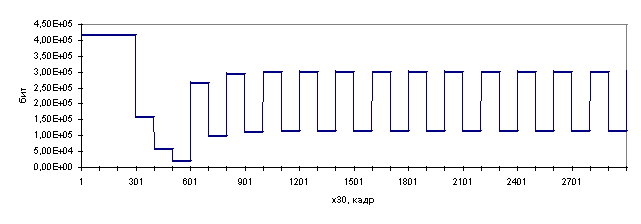
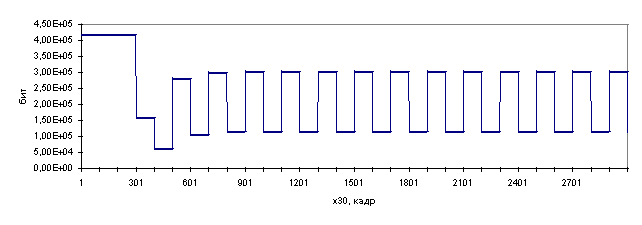
ж) задержка 2550 кадров
Рис. 3.3. Иллюстрация процесса поиска оптимального значения
параметра![]() при
различных значениях задержки управления
при
различных значениях задержки управления
В результате проведенного численного моделирования установлено, что при задержке управления более 500 кадров, коммутатор начинает терять кадры. При задержке в 1500 кадров, потери достигают 40%.
3.3. Анализ результатов
Сравнение графиков (рис. 3.1а и рис. 3.2б-е) показывает адекватность функционала (2.21) качества управления и его высокую чувствительность. В силу этого, анализ оптимальности системы управления в целом на основе функционала получается более точным по сравнению с анализом на основе параметров динамики коммутатора.
Данные рис. 3.2а подтверждают выводы работы [1], что задержка управления практически не сказывается на уровне загрузки выходного порта коммутатора. Этот факт говорит об автономности систем управления потоком кадров, очередями, и арбитражем коммутационной матрицы (шины), что облегчает задачу синтеза качественных алгоритмов управления очередями и арбитражем коммутационной матрицы (шины).
Сравнительный анализ результатов моделирования синтезированной системы управления (рис. 3.1 и 3.2) и стандартной [1], показывает, что по всем динамическим параметрам разработанная система превосходит стандартную. Особенно наглядно это видно из рис. 3.4, на котором приведены зависимости функционала оптимальности (2.21) от задержки управления для синтезированной (AFC) и стандартной (802.3x) системы управления.
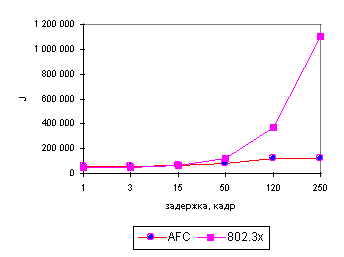
Рис. 3.4. Сравнительная зависимость функционала оптимальности
от задержки управления для синтезированной и стандартной САУ
Анализ кривых на рис. 3.4 показывает, что на дистанциях менее 2 км (табл. 3.1), синтезированная система управления, по качеству управления ничем не отличается от стандартной, но обладает большей сложностью. На дистанциях более 20 км (табл. 3.1), разница в качестве управления становится весьма существенной. Сравнение данных приведенных на рис. 3.2в, с аналогичными данными из работы [1] показывает, что разработанная система обладает лучшими стабилизирующими свойствами, по сравнению со стандартной. А сравнение данных рис. 3.2г, с аналогичными из работы [1] демонстрирует, что контура адаптации эффективно нейтрализуют транспортное запаздывание (до 500 кадров), приводя к более равномерному управлению, и снижают выбросы перерегулирования. Это положительно влияет на снижение значений джиттера (рис. 3.2е), важного параметра характеризующего качество обслуживания, особенно при передаче через сеть видеоинформации и голоса [4].
Одним из главных параметров определяющих качество обслуживания является вероятность потери кадра [4]. Размер буфера и динамика поведения очереди являются основными величинами влияющими на этот показатель. Принимая во внимание, что при задержке управления более 500 кадров, коммутатор начинает терять кадры. И то, что при таких задержках в линии накапливается в среднем более 500 КБ «неуправляемыхЛ данных. А также тот факт, что уровень потерь не зависит от закона управления (и для стандартной и для синтезированной системы уровень потерь одинаков). Можно сделать вывод о неприемлемости применяемого подхода к управлению потоком кадров на магистральных каналах протяженностью свыше 500 км. Вывод о неприемлемости подхода подтверждает сравнение значений функционала оптимальности приведенных на рис. 3.1а и 3.1б. В зоне где начинаются потери кадров (выход за конструкционные ограничения) функционал оптимальности возрастает в 650 раз. Здесь необходимо отметить, что даже в этой зоне, значение функционала оптимальности синтезированной системы управления меньше значения функционала стандартной системы [1] в 6,1-2,9 раза, что говорит о ее лучшем качестве.
Сравнительный анализ данных приведенных на рис. 3.3
показывает, что с возрастанием задержки управления процесс поиска
оптимального значения параметра![]() меняется
существенным образом, это объясняется наложением на процесс поиска
вертикального дрейфа экстремума, возникающего из-за стохастичного характера
входных и возмущающих воздействий объекта управления.
меняется
существенным образом, это объясняется наложением на процесс поиска
вертикального дрейфа экстремума, возникающего из-за стохастичного характера
входных и возмущающих воздействий объекта управления.
4. ВЫВОДЫ
В процессе проведенных в работе исследований получены следующие основные результаты:
1. Создана новая адаптивная система управления потоком кадров в сетях Gigabit Ethernet, более оптимальная по критерию качества обслуживания нежели стандартная IEEE 802.3x.
2. Синтезирован новый закон управления учитывающий уровень загрузки коммутационного устройства и среднее значение межкадрового интервала при расчете значений управляющей переменной.
3. Разработан новый алгоритм поисковой адаптации параметров закона управления для учета им задержки управления возникающей на магистральных каналах связи.
4. Показано, что применение разработанной системы управления на каналах связи протяженностью до 120 км, практически не влияет на показатели качества обслуживания в отличие от стандартной системы управления [1]. Данный результат делает возможным применение технологии Gigabit Ethernet на загруженных мультисервисных сетях городского и внутризонового масштаба.
5. Подтвержден результат работы [1], что при применении Gigabit Ethernet на магистральных каналах протяженностью свыше 500 км, требуется разработка иного подхода к управлению потоком кадров, так как схема применяемая схема управления допускает значительные потери кадров (более 40 %). По всей видимости более оптимальным решением является разработка нового подхода к управлению потоком кадров не для Gigabit Ethernet, а для разрабатываемой в настоящее время технологии на 10 Gigabit Ethernet. Применение именно этой технологии более вероятно на магистральных зоновых сетях в комбинации c DWDM [5].
В настоящий момент проводится расширение синтезированной системы управления потоком кадров для учета ею класса и приоритета проходящего трафика. И модификация закона управления для целенаправленного воздействия на узлы вызывающие перегрузку.
Также разрабатывается
модель чувствительности, для нахождения оптимальных значений нормирующего
коэффициента![]() и
ширины окон усреднения
и
ширины окон усреднения![]() ,
,![]() ,
,![]() и
и![]() .
.
5. ЛИТЕРАТУРА
1. Макаренко А. В. Влияние задержки управляющего сигнала на оптимальность системы управления потоком кадров IEEE 802.3x.// Интернет публикация – Журнал Радиоэлектроники, р 12, 2001. – http://jre.cplire.ru/jre/dec01/5/text.html
2. Нетес В. А. Качество обслуживания на сетях связи. Обзор рекомендаций МСЭ-Т. – Журнал «Сети и системы связиЛ, р3, 1999. – 66-71 стр.
3.
IEEE
802.3x. 1998 Edition. IEEE standards for Local Area Networks: Advanced Flow
Control.
4.
Kaplan R.
«U. S. Metropolitan Ethernet Services Market Forecast and Analysis,
2001-2006Л. IDC Report #W249801, July 2001.
5. Энди Дорнани. Ethernet выходит в глобальные сети. – Журнал «LAN. Сетевые решенияЛ, р11, 2000. – 52-57 стр.
6. Техническая кибернетика. Теория автоматического регулирования. Т. 1./Под ред. В. В. Солодовникова. – М.: Машгиз, 1954.
7. Макаренко А. В. Модель динамики коммутатора Gigabit Ethernet.// Интернет публикация – Журнал «РадиоэлектроникиЛ, р 11, 2001. – http://jre.cplire.ru/jre/nov01/2/text.html
8.
Справочник по теории
автоматического управления, под ред. А. А. Красовского. – М.: Наука. Гл.
Ред. Физ.-мат. Лит.,
1987. – 712 с.
9.
Paxson
V., Floyd S., «Wide-Area Traffic: The Failure of Poisson ModelingЛ, ACM
SIGCOM'94, pp. 257-268, 1994.
10.
Garett
M., Willinger W., «Analysis, Modeling and Generation of Self-Similar VBR
Video TrafficЛ, SIGCOMM'94, pp. 269-280, 1994.
11.
Leland W.
E., Taqqu M. S., Willinger W., Wilson D., «On the self-similar nature of
ethernet trafficЛ, Proc/ ACM SIGCOMM'93, pp. 183-193, 1993.
12. Кучерявый Е. А., Яновский Г. Г., Метод прогнозирования мультимедийного трафика в сетях АТМ. Тезисы конференции «Информационные сети и системыЛ, Москва, октябрь 26-27, 1999, с. 9.
13. Казаков И. Е., Гладков Д. И. Методы оптимизации стохастических систем. – М.: Наука, гл. ред. физ-мат. лит., 1987. – 304 с.
14.
IEEE Std
802.3. 2000 Edition. IEEE standards for Local and Metropolitan Area
Networks: Part 3: Carrier sense multiple access with collision detection (CSMA/CD)
access method and physical layer specifications.
15. Розенвассер Е. Н., Юсупов Р. М. Чувствительность систем управления. – М.: Наука, 1981.
16. Казакевич В. В. Способ автоматического регулирования различных процессов по максимуму или минимуму. Авторское свидетельство р 66335 от 25 ноября 1943 гг.
17. Казакевич В. В. Об экстремальном регулировании. Диссертация на соискание ученой степени кандидата технических наук, МВТУ, 1944.
18. Васильев Ф. П. Численные методы решения экстремальных задач: Учеб. Пособие для вузов. – 2-е изд. Перераб. и доп. – М.: Наука, Гл. Ред. физ.-мат. лит., 1988. – 552с.
19. Техническая кибернетика. Теория автоматического регулирования. Т. 3. часть II./Под ред. В. В. Солодовникова. – М.: Машгиз, 1969.
20. Казакевич В. В. Системы экстремального регулирования и некоторые способы улучшения их качества и устойчивости. Сб. «Автоматическое управление и вычислительная техникаЛ. М., Машгиз, 1958.
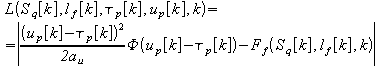 ,
,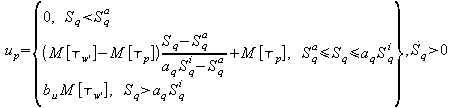 ,
(2.29а
,
(2.29а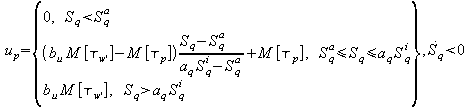 .
.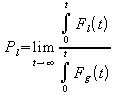 .
(3.1)
.
(3.1)