УДК 537.8

ДИЭЛЕКТРИЧЕСКАЯ РЕЛАКСАЦИЯ В ВОЛОКНИСТОМ КОМПОЗИТЕ ПОЛИЭТИЛЕН/ФЕРРИТ

 

А. А. Паньков

Пермский национальный исследовательский политехнический университет

 

Получена 1 февраля 2014 г.

 

Аннотация. Исследовано влияние толщины прослойки полиэтилена между однонаправленными ферритовыми волокнами и частоты электрического поля на эффективную диэлектрическую проницаемость и проводимость полидисперсного композита с учетом максвелл-вагнеровской релаксации. Приведены графики частотных зависимостей эффективных констант и диаграмм Коула-Коула композита. Подтвержден недебаевский характер диэлектрической релаксации в полидисперсных матричных структурах.

Ключевые слова: максвелл-вагнеровская релаксация, композит, эффективные свойства, полидисперсная структура.

Abstract. Influence of the thickness of a layer of polyethylene between unidirectional ferrite fibers and frequencies of electric field on effective dielectric permeability and conductivity of a polydisperse composite taking into account maksvell-wagner relaxation is investigated. Schedules of frequency dependences of effective constants and Cole-Cole's charts of the composite are provided. Not Debye character of a dielectric relaxation in polydisperse matrix structures is confirmed.

Key words: maxwell‑wagner relaxation, composite, effective properties, polydisperse structure.

 

Введение

В [1] для аппроксимации экспериментальных частотных зависимостей действительной и мнимой частей диэлектрической проницаемости поликристаллической керамики (рис.1,а) использована подгонка варьируемых параметров равновероятного распределения времен релаксации. В [1] в частности отмечено, что физической основой модели может быть максвелл – вагнеровская поляризация и релаксация [2‑6] в электрически неоднородной матричной системе из зерен, окруженных тонкими слоями с малой [7] проводимостью и отличной от зерен диэлектрической проницаемостью; вариация проницаемостей, проводимостей, размера зерен и толщин оболочек вокруг них приводит к широкому распределению времен релаксации и обуславливает большие величины диэлектрической проницаемости и проводимости и недебаевскую релаксацию в поликристаллическом материале.

Цель работы – подтвердить недебаевский характер диэлектрической релаксации в полидисперсных матричных структурах и исследовать влияние толщины прослойки полиэтилена между ферритовыми волокнами и частоты электрического поля на эффективную диэлектрическую проницаемость и проводимость композита.

 

а           б                 в                  г

Рис. 1 Фрагменты реальной [1] (а), моделей (б)-(г) полидисперсных структур

1. Диэлектрическая проницаемость композита. Самосогласованные решения

Методы самосогласования [8‑12] представляют одно из направлений механики композитов и основаны на учете многочастичного взаимодействия между волокнами композита через замену неоднородной среды, окружающей произвольное волокно, например, без учета или с учетом прилегающей к нему прослойкой матрицы однородной анизотропной средой с искомыми эффективными свойствами композита. Полученные таким образом расчетные схемы: одиночное включение в эффективной среде и одиночное включение с прослойкой матрицы в эффективной среде, с заданным на большом удалении от волокна однородным полем макронапряженности электрического поля, позволяют рассчитать эффективные диэлектрические проницаемости композитов с соответствующими полидисперсными структурами (рис.1). В полидисперсных структурах распределение ячеек (поперечных сечений однофазных на рис.1,г и составных двухфазных на рис.1,б,в цилиндров) по размерам достаточно широко, включая и бесконечно малые, что обуславливает возможность заполнения такими полидисперсными ячейками всей представительной области композита.

Для рассматриваемых моделей (рис.1,б-г) полидисперсных структур относительное число ячеек с волокнами (1-я фаза) , где относительное объемное содержание 1-й фазы (волокон) в композите , величина прослойки  матрицы (2-я фаза) может принимать значения

,                                          (1)

до максимально возможного значения , отношение радиусов  волокна  и ячейки  не зависит от абсолютных размеров ячейки, объемная доля волокна в произвольной ячейке с волокном . В предельных случаях: ,  (рис.1,б), ,  (рис.1,г).

Полидисперсные структуры (рис.1,б,в) сохраняют свойство матричности 2-й фазы при всех возможных степенях наполнения  композита 1-й фазой для всех значений . Лишь в случае  (рис.1,г) свойство матричности исчезает и структура становится инвариантной к инверсии свойств 1-й и 2-й фаз при фиксированных объемных долях обеих фаз:  и .

Интерес к исследованию полидисперсных моделей обусловлен возможностью получения точных, в рамках модели, аналитических решений [8,9] для эффективных констант, в частности диэлектрических проницаемостей композита.

Для полидисперсной структуры на рис.1, с трансверсально-изотропными диэлектрическими проницаемостями обеих фаз решение для эффективной диэлектрической проницаемости в плоскости изотропии

                                            (2)

может быть получено из расчетной схемы: одиночное волокно с прослойкой матрицы толщиной в эффективной среде [9], нагруженной поперечным, например, вдоль оси  электрическим полем как решение квадратного уравнения

,

в решении (2) которого

,   ,   ,   ,

,   ,

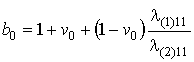разность , диэлектрические проницаемости фаз: , .

         Для случая отсутствия прослойки () в структуре на рис.1,г, в решении (2) для эффективной диэлектрической проницаемости  коэффициенты

,   ,    

Решение для эффективной продольной диэлектрической проницаемости всех структур (рис.1,б‑г)

                                       (3)

совпадает с решением Фойгта и не зависит от толщины прослойки , оператор осреднения по объему композита .

Отметим, что известные [2] решения ,  или границы Хашина-Штрикмана для поперечных диэлектрических проницаемостей однонаправленного двухфазного волокнистого композита

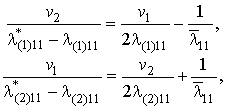                                         (4)

для продольной диэлектрической проницаемости  (3).

Учет проводимостей  фаз  и частоты  приложенного электрического поля через комплексную форму записи [2‑6]

                                                           (5)

тензоров диэлектрических проницаемостей  фаз с действительными частями  приводит к комплексному виду тензора эффективных диэлектрических проницаемостей (2) композита

  ,                                                              (6)

где мнимая часть  выражается через действительную часть  эффективной проницаемости композита

                                                        (7)

Для четкого выделения релаксационных максимумов исключим из мнимой части эффективной диэлектрической проницаемости  сингулярную составляющую, обусловленную статической при  или «сквозной» [1] проводимостью

,

и найдем релаксационные максимумы из анализа частотной зависимости вспомогательной функции

                                              (8)

 

2. Численный расчет

Рассмотрим однонаправленный волокнистый композит с полидисперсной структурой: 1-я фаза ‑ феррит (волокна), 2-я фаза – полиэтилен (матрица). Волокна ориентированы вдоль координатной оси , плоскость изотропии . Диэлектрическая проницаемость  и проводимость  (Ом×м)^-1 полиэтилена [13], для феррита:  (Ом×м)^-1 [14],  (5), где диэлектрическая проницаемость вакуума  Ф/м.

На рис.2 приведены результаты расчета действительной  (сплошная линия) и мнимой  (пунктирная линия) частей (6) эффективной диэлектрической проницаемости  (рис.2,а) (2), мнимой части с вычетом сквозной проводимости  (рис.2,б) (8), действительная часть (7) полной проводимости  (рис.2,в) композита при объемной доле ферритовых волокон  для различных значений прослоек  (1) между волокнами:  (),  (),  (),  (),  (); границы Хашина-Штрикмана (-) и (+) (4). Отметим, что решения (+) и () совпадают для всех значений ,  и на рис.2,б использована логарифмическая шкала для частоты  по аналогии [1].

 

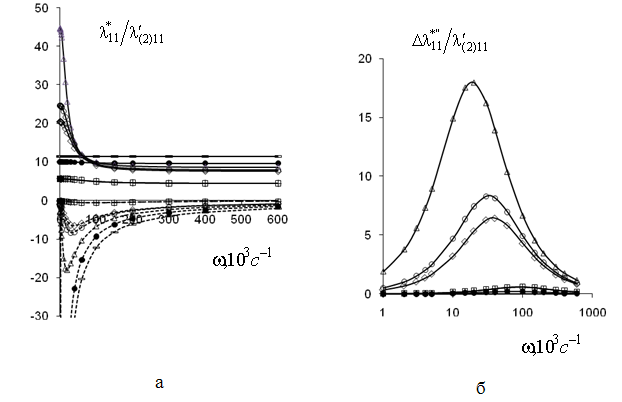
Рис.2 Частотные зависимости эффективной диэлектрической проницаемости  (а), разности  (б) и проводимости  (в) композита

 

3. Выводы

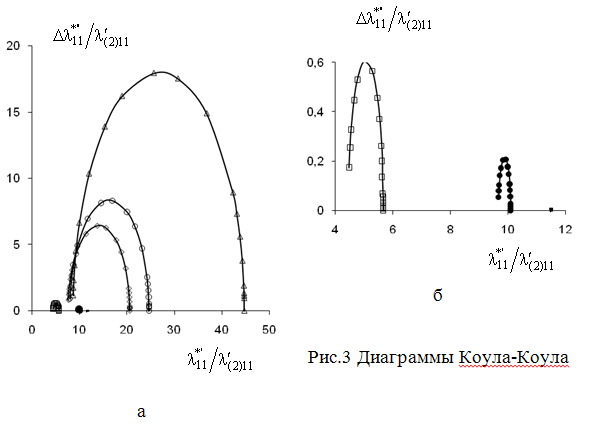
Наличие явно выраженных максимумов у кривых на рис.2,б свидетельствует о протекании в композите релаксационного процесса, а вид диаграмм Коула-Коула (рис.3) указывает на недебаевскую релаксацию [1]. Вид графиков на рис.2, рис.3 хорошо согласуются с экспериментальными данными в [1]. В предельном случае, при устремлении толщины прослойки к нулю () решения для эффективной диэлектрической проницаемости  и проводимости  стремятся к соответствующим решениям для случая  с расчетной схемой – волокно в эффективной среде лишь в высокочастотном случае при . В низкочастотном случае, особенно при , наличие даже бесконечно малых прослоек  очень существенно влияет на значения эффективных констант  и  композита и на отличие в несколько раз от соответствующих решений при  (рис.2). Все решения для мнимой части диэлектрической проницаемости  (рис.2,а) и действительной части проводимости  (рис.2,в) композита, полученные при варьировании толщины прослойки , лежат внутри соответствующих границ Хашина-Штрикмана. Решения для действительной части  попадают в эти границы лишь при высоких значениях частоты  (рис.2,а).

 

Литература

1.     Павленко А.В., Турик А.В., Резниченко Л.А., Шилкина Л.А., Константинов Г.М. Диэлектрическая релаксация в керамике PbFe_1/2Nb_1/2O₃ // Физика твердого тела. –  2011. – Т. 53, № 9. – С. 1773–1776

2.     Виноградов А.П. Электродинамика композитных материалов. – М.: Эдиториал УРСС, 2001. – 208 с.

3.     Турик А.В., Радченко Г.С., Чернобабов А.И., Турик С.А. Диэлектрическая проницаемость полимерных матриц, содержащих изолированные включения: гигантское диэлектрическое усиление вместо коллективного резонанса // Письма в ЖЭТФ. – 2004. – Т. 79, № 9. – С.512–514

4.     Соцков В.А. Экспериментальная оценка концентрационной зависимости действительной части диэлектрической проницаемости в неупорядоченной макросистеме парафин-графит // Письма в ЖТФ. – 2004. – Т. 30, № 12. – С.1‑5

5.     Pan’kov A.A. Maxwell–wagner relaxation in fibrous polydisperse magnetoelectric piezocomposites // Mechanics of Composite Materials. – 2013. – Vol. 49, № 1. –pp.45‑50

6.     Паньков А.А. Максвелл-вагнеровская релаксация в пьезокомпозите PVF/феррит с эллипсоидальными включениями в переменном электрическом поле // Журнал радиоэлектроники: электронный журнал. –2013. – №6. URL: http://jre.cplire.ru/jre/jun13/12/text.pdf

7.     Raevski I.P., Prosandeev S.A., Bogatin A.S., Malitskaya M.A., Jastrabik L. // J. Appl. Phys. 93, 4130 (2003)

8.     Кристенсен Р. Введение в механику композитов. – М.: Мир, 1982. – 334 с.

9.     Паньков А.А. Методы самосогласования механики композитов. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. – 253 с.

10. Pan'kov A.A. A self-consistent statistical mechanics approach for determining effective elastic properties of composites // Theoretical and Applied Fracture Mechanics. – 1999. – Vol. 31, № 3. – pp.157–161

11. Pan'kov A.A. A generalized self-consistent method for composites with random elastic properties of inclusions // Mechanics of Composite Materials. – 1999. – Vol. 35, № 6. – pp.513–520

12. Паньков А.А. Самосогласованные решения для коэффициентов электромагнитной связи волокнистого пьезокомпозита // Механика композиционных матеpиалов и констpукций. – 2013. – Т.19, №2. – С.233–243

13.  Турик А.В., Радченко Г.С. Гигантский пьезоэлектрический эффект в слоистых композитах сегнетоэлектрик-полимер // Физика твердого тела. – 2003. – Т. 45, № 9. – С.1676–1679

14. Петров В.М., Бичурин М.И., Srinivasan G. Максвелл-вагнеровская релаксация в магнитоэлектрических композиционных материалах // Письма в ЖТФ. – 2004. – Т. 30, № 8. – С.81–87