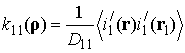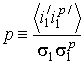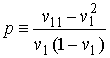УДК 537.8

ВЛИЯНИЕ РАЗУПОРЯДОЧЕННОСТИ И ИНВЕРСИИ ФАЗ НА ЭЛЕКТРОМАГНИТНУЮ СВЯЗАННОСТЬ ПЬЕЗОКОМПОЗИТА С КВАЗИПЕРИОДИЧЕСКОЙ СТРУКТУРОЙ

 

А. А. Паньков

Пермский национальный исследовательский политехнический университет

 

Получена 10 января 2014 г.

 

Аннотация. Дан анализ двухточечных корреляционных функций случайной квазипериодической структуры и получены аналитические решения для тензоров эффективных свойств квазипериодических пьезоэлектромагнитных композитов в виде линейной комбинации известных соответствующих решений для тензоров эффективных свойств композитов с идеально периодической и полидисперсной структур. В новые решения вошел «коэффициент периодичности» ‑ коэффициент корреляции квазипериодической и периодической структур. Представлен численный анализ влияния разупорядоченности и инверсии свойств фаз на значения продольного коэффициента электромагнитной связи композита с квазипериодической однонаправленной волокнистой структурой из пьезоэлектрической (PVF) и пьезомагнитной (феррит) фаз. Выявлены новые эффекты и проведено сравнение результатов расчета с известными решениями других авторов.

Ключевые слова: пьезокомпозит, электромагнитоупругость, эффективные свойства, квазипериодическая структура.

Abstract. The analysis of point-to-point correlation functions of casual quasiperiodic structure is given and analytical decisions for tensors of effective properties of quasiperiodic piezoelectro-magnetic composites in the form of a linear combination of the known relevant decisions for tensors of effective properties of composites from ideally periodic and polydisperse structures are received. New decisions included "frequency coefficient", this is coefficient of correlation of quasiperiodic and periodic structures. The numerical analysis of influence of aperiodicity and inversion of properties of phases on values of longitudinal coefficient of electromagnetic communication of a composite with quasiperiodic unidirectional fibrous structure from piezoelectric (PVF) and piezomagnetic (ferrite) of phases is submitted. New effects are revealed and comparison of results of calculation with known decisions of other authors is carried out.

Keywords: piezocomposite, electro-magnetic elasticity, effective properties, quasiperiodic structure.

 

Введение

Магнитоэлектрические константы гомогенных магнитоэлектриков очень малы, что обуславливает создание гетерогенных композиционных магнитоэлектриков магнитоэлектрические константы которых могут на несколько порядков превосходить соответствующие константы гомогенных материалов [1,2]. Ранее в [3] проведен численный анализ влияния на действительные и мнимые части эффективных коэффициентов электромагнитной связи полидисперсного [4] электромагнетика PVF/феррит формы эллипсоидальных ферритовых включений и максвелл-вагнеровской релаксации фаз в переменном электрическом поле.

Цель работы ‑ исследование влияния разупорядоченности и инверсии свойств фаз на эффективный коэффициент продольной электромагнитной связанности однонаправленного волокнистого пьезокомпозита PVF/феррит и феррит/PVF с квазипериодической структурой.

 

1. Модели структур и корреляционные функции

 

 

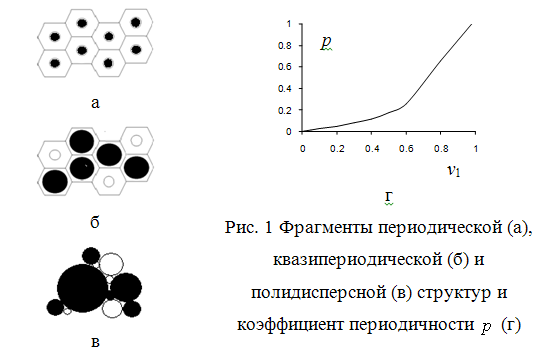
Нормированная корреляционная функция квазипериодической двухфазной структуры (рис.1,б)

                                            (1)

 

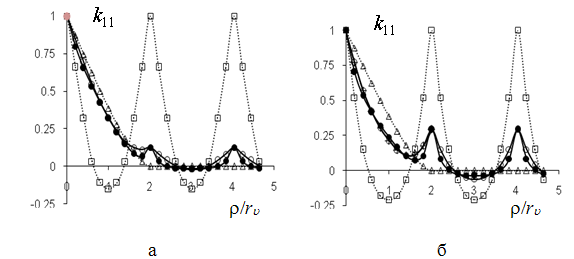
может быть представлена [5,6] аппроксимирующим разложением (рис.2)

                                 (2)

 

 

где вектор разности , точки , пульсация  индикаторной функции  со значениями 1 и 0 соответственно в 1-й и 2-й фазах композита, относительное объемное содержание 1-й фазы  в области  композита, оператор статистического осреднения  совпадает с осреднением по представительной области  с учетом статистической однородности и эргодичности [7] структур. В формулу (2) вошел коэффициент корреляции квазипериодической и периодической структур

                                                                (3)

где среднеквадратические отклонения , , нормированные корреляционные функции периодической структуры (рис.1,а)

 

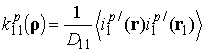
и полидисперсной структуры (рис.1,в)

;

 

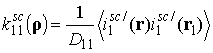здесь и далее верхние индексы «» и «» указывают на принадлежность к периодической и полидисперсной структурам.

 

Рис.2 Нормированные корреляционные функции для периодической (), полидисперсной (), квазипериодической () структур при  (а),  (б); () – аппроксимация для ()

 

Начальные значения: , дисперсии  с учетом равенств  объемных долей волокон во всех трех структурах. Отметим, что коэффициент корреляции или «периодичности» [5,6]  в (2), (3) рассчитывается

                                                   (4)

через одноточечный момент  ‑ среднее от произведения индикаторных функций 1-й фазы (включений) в квазипериодической  и периодической  структурах. Геометрический смысл момента  ‑ это относительное объемное содержание области пересечения включений квазипериодической и периодической структур при их мысленном наложении друг на друга как следствие из свойства статистической однородности и эргодичности индикаторных функций. В [5] приведены аналитические решения для  и  (4) как функций относительного объемного содержания включений  различных квазипериодических структур с ориентированными эллипсоидальными, сферическими, пластинчатыми включениями и однонаправленными волокнами при различных типах разупорядоченности элементов структуры.

 

2. Эффективные свойства композита

Пусть представительная область  композита с квазипериодической структурой состоит из двух () однородных пьезоэлектромагнитных фаз с заданными тензорами упругих , пьезоэлектрических  и пьезомагнитных  свойств, диэлектрических  и магнитных  проницаемостей, температурных коэффициентов , пироэлектрических  и пиромагнитных  постоянных.

Искомое решение

для тензоров эффективных свойств: , …,  и коэффициентов электромагнитной связи ,  квазипериодического композита, входящих в определяющие соотношения на макроуровне композита

,

,

,

можно выразить в виде [3,5-8]

                    (5)

или с учетом в (5) лишь первого или «корреляционного» [7,8] приближения

,                                                      (6)

где макроскопические значения напряжений  и деформаций , индукций ,  и напряженностей , , однородное приращение температуры , вызванное внешним нагревом.

После подстановки разложения (2) в (6)

получим искомое решение

                                        (7)

с учетом линейности оператора

и известных решений

,                                (8)

для тензоров эффективных свойств композитов с периодической (рис.1,а)

и полидисперсной (рис.1,в)

структурами аналогично (6). Решение  для периодической структуры может быть получено на ячейке периодичности [9],  для полидисперсной структуры ‑ по схеме самосогласования «одиночное волокно в эффективной среде» [4,10] или как частные случаи обобщенного сингулярного приближения [3,8].

В частности, тензор эффективной электромагнитной связи композита

,                            (9)

компоненты оператора

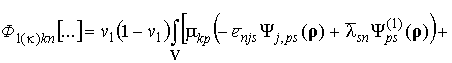
с учетом вида корреляционного приближения для компонент искомого тензора

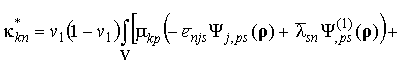          (10)

тензоры разностей

,   ,…,    .

Отметим, что в [3] получены сингулярные составляющие вторых производных функций Грина: , , ,  (10) для однородной пьезоэлектромагнитной трансверсально-изотропной среды.

 

3. Численный расчет

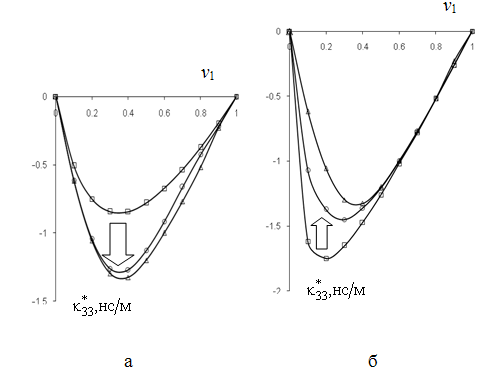
Проведем расчет (9) и анализ влияния разупорядоченности и инверсии свойств фаз на значения продольного коэффициента электромагнитной связи  ((), рис.3) волокнистого композита с квазипериодической структурой (рис.1,б) из пьезоэлектрической (PVF) и пьезомагнитной (феррит) фаз; свойства PVF и феррита приведены в [3,11,12]. Необходимые для этого значения коэффициентов для периодической  (рис.1,а; (), рис.3) и полидисперсной  (рис.1,в; (), рис.3) структур рассчитываем по формулам [3] обобщенного сингулярного приближения, приравнивая свойства «среды сравнения» [8] соответственно к свойствам матричной фазы или к искомым эффективным свойствам  (8) («схема самосогласования») композита.

Рис. 3 Коэффициент электромагнитной связи  композита феррит/PVF (а) и PVF/феррит (б) в зависимости от доли  пьезоэлектрика PVF в виде волокон (а), матрицы (б)

 

Справедливость такого подхода для периодической структуры подтверждена сравнением результатов расчета с известным аналитическим решением [1]: решение () на рис.3,а для  композита феррит/PVF обобщенного сингулярного приближения в точности совпало с решением [1] асимптотического метода осреднения для идеальной периодической волокнистой структуры. Решение по схеме самосогласования () (рис.3) в точности совпало с известным решением [10] по модели «одиночное волокно в эффективной среде» [4]; отметим, что решение () по схеме самосогласования инвариантно к инверсии свойств фаз. Стрелки на рис.3 показывают направления изменений значений коэффициента  композита при разупорядочивании периодической структуры (). Отметим, что полученные результаты расчетов соответствуют высокочастотному случаю нагружения композита, при котором влияние максвелл-вагнеровских релаксационных процессов [2,3] пренебрежимо мало.

 

4. Выводы

На основе анализа (рис.2) двухточечных корреляционных функций (1) случайной квазипериодической структуры (рис.1,б) предложена их аппроксимация (2) через корреляционные функции идеально периодической (рис.1,а) и предельно полидисперсной (рис.1,в) структур. Далее получено аналитическое решение (7) для тензоров эффективных упругих свойств, диэлектрической и магнитной проницаемостей, пьезомеханических свойств, коэффициентов электромагнитной связи и температурных напряжений, вектора эффективных пироэлектрических и пиромагнитных постоянных квазипериодических пьезоэлектромагнитных композитов в виде линейной комбинации известных соответствующих решений для тензоров эффективных свойств композитов с идеально периодической и полидисперсной структур. В новые решения вошел «коэффициент периодичности» (рис.1,г), (3), (4) ‑ коэффициент корреляции квазипериодической и периодической структур. Представлен численный анализ (рис.3) (9) влияния разупорядоченности и инверсии свойств фаз на значения продольного коэффициента  электромагнитной связи композита с квазипериодической однонаправленной волокнистой структурой из пьезоэлектрической (PVF) и пьезомагнитной (феррит) фаз. Проведено сравнение результатов расчета с известными решениями других авторов [1]. Выявлены новые эффекты ‑ привнесение разупорядоченности в идеальную периодическую однонаправленную волокнистую структуру по разному влияет на характер и величину изменения абсолютного значения продольного коэффициента  электромагнитной связи композита и значительно до 50% увеличивает  для композита феррит/PVF (рис.3,а) и менесоответственно к свойствам матричной фазы или к искомым эффективным свойствам  (8) («схема самосогласования») композита. е существенно до 25% уменьшает  для композита PVF/феррит (рис.3,б) при средних и высоких степенях наполнения композита пьезоэлектрическими или ферритовыми волокнами соответственно. При малых (менее 30%) объемных долях как пьезоэлектрических, так и ферритовых волокон влияние их разупорядоченности на значения  композита практически незаметно, так как отсутствует взаимодействие между далеко расположенными соседними волокнами и справедлива известная [4] гипотеза о невзаимодействии включений. Результаты расчета на рис.3 показывают, что для увеличения абсолютных значений коэффициента  электромагнитной связи композита лучше использовать пьезоэлектрик PVF в качестве матрицы, а феррит в виде волокон с периодической укладкой и с высокой около 80% объемной долей (рис.3,б).

 

Литература

1.    Гетман И.П. О магнитоэлектрическом эффекте в пьезокомпозитах // ДАН СССР. – 1991, Т.317, №2. – c.341–343

2.    Турик А.В., Чернобабов А.И., Родинин М.Ю. Гетерогенные мультиферроики: магнитоэлектричество и пьезоэффект // Физика твердого тела, 2009, Т.51, №8. – С. 1580‑1583

3.    Паньков А.А. Максвелл-вагнеровская релаксация в пьезокомпозите PVF/феррит с эллипсоидальными включениями в переменном электрическом поле // Журнал радиоэлектроники: электронный журнал. 2013. №6. URL: http://jre.cplire.ru/jre/jun13/12/text.pdf

4.    Кристенсен Р. Введение в механику композитов. – М.: Мир, 1982. – 334 с.

5.    Паньков А.А. Механика пьезокомпозитов. Электро- и магнитоупругость неоднородных сред. ‑ LAP LAMBERT Academic Publishing, 2011. ‑ 476c.

6.    Паньков А.А. Упругие свойства квазипериодических композитов с учетом корреляционных функций структуры // Механика композиционных матеpиалов и констpукций. – 2011. ‑ Т. 17, № 3. – С. 385‑400

7.      Волков С.Д. Статистическая механика композитных материалов / С.Д. Волков, В.П. Ставров. – Минск: Изд-во Белорус. гос. ун-та, 1978. - 208с.

8.      Шеpмеpгоp Т.Д. Теоpия упpугости микpонеодноpодных сpед. ‑ М.: Наука, 1976. ‑ 399 с.

9.      Победря Б.Е. Механика композиционных материалов. ‑ М.: Изд-во Моск. университета, 1984. ‑ 336 c.

10.  Паньков А.А. Самосогласованные решения для коэффициентов электромагнитной связи волокнистого пьезокомпозита // Механика композиционных матеpиалов и констpукций, 2013, Т.19, №2. ‑ С.233‑243

11. Хорошун Л.П., Маслов Б.П., Лещенко П.В. Прогнозирование эффективных свойств пьезоактивных композитных материалов. – Киев: Наук. думка, 1989. – 208 с.

12. Sessler G.M. Piezoelectricity in polyvinylidenefluoride // J. Acoust. Soc. Amer. ‑ 1981, Vol. 70, № 6. ‑ pp.1596‑1608.