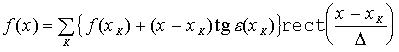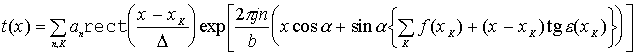5. Ограничения метода
В общем случае, если сигнал промодулирован несущей частотой, то для его восстановления необходима соответствующая фильтрация. Естественно, что это относится как к электрическим, так и оптическим сигналам. При этом восстановление исходного сигнала возможно, если выполняется теорема выборки [18]. Отметим, что изображение кодируется различными несущими частотами, причем распределение частот зависит от формы объекта, периода решетки и топологии схемы кодирования. Поэтому условия восстановления сигнала будут отличны от обычной теоремы Котельникова [19]. Чтобы убедиться в этом, рассмотрим для простоты случай функции рельефа, зависящей только от одной переменной X.
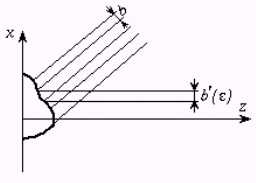
Пусть объект освещается системой полос с периодом ![]() (рис.
7). Если увеличение оптической системы
формирования изображения равно 1, то соотношение между пространственной
частотой
(рис.
7). Если увеличение оптической системы
формирования изображения равно 1, то соотношение между пространственной
частотой ![]() записанных полос и углом
записанных полос и углом ![]() можно представить как
можно представить как
При этом максимальная пространственная частота ![]() , соответствующая
максимальному углу
, соответствующая
максимальному углу ![]() , и минимальная
пространственная частота
, и минимальная
пространственная частота ![]() , соответствующая
минимальному углу
, соответствующая
минимальному углу ![]() , будут равны
, будут равны
Итак, проблема восстановления сигнала заключается в определении связи между
функцией рельефа ![]() , которая содержит
наивысшую частоту
, которая содержит
наивысшую частоту ![]() , с ее
ограничивающим углом
, с ее
ограничивающим углом ![]() и периодом полос
и периодом полос ![]() на изделии. Используя обычную теорему
выборки, можно описать функцию рельефа
на изделии. Используя обычную теорему
выборки, можно описать функцию рельефа ![]() как
как
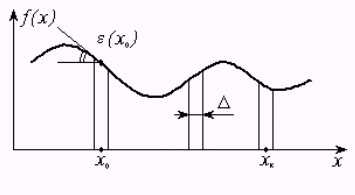
где ![]() — фиксированная точка и
— фиксированная точка и ![]() представляет тангенциальный угол в этой точке
(рис. 8). Полная функция
представляет тангенциальный угол в этой точке
(рис. 8). Полная функция ![]() может быть восстановлена путем собирания
функции из малых сегментов длиной Dи выполнения суммирования по всем этим
сегментам, т. е.
может быть восстановлена путем собирания
функции из малых сегментов длиной Dи выполнения суммирования по всем этим
сегментам, т. е.
Подставив (26) в (8), получим следующее выражение для амплитудного пропускания транспаранта
(28)
C учетом определения функции 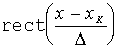 ее в выражении (28) можно вынести вперед
экспоненциального члена. В результате (28) можно переписать как
ее в выражении (28) можно вынести вперед
экспоненциального члена. В результате (28) можно переписать как
(29)
В частотной же плоскости системы обработки информации амплитудное распределение от такого транспаранта будет пропорционально
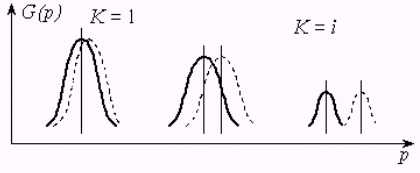
Графическое представление выражения (30) показано на рис. 9. Пренебрегая фазовыми членами, которые несущественны для перекрытия порядков n, из рис. 9 видно, что суммирование индексов K является определяющим для точного разделения дифракционных порядков.
Рис. 7. Схематическое представление изменения
наблюдаемого периода ![]() от угла
от угла ![]() .
.
Рис. 8. Геометрическая связь угла рельефа ![]() с функцией рельефа
с функцией рельефа ![]() .
.
Рис. 9. Пояснение к распределению дифракционных порядков в частотной плоскости системы обработки для двух различных значений K.
При этом точное разделение дифракционных порядков может быть достигнуто с
учетом максимального значения ![]() и минимального значения
и минимального значения ![]() тангенциального угла
тангенциального угла ![]() рельефа
рельефа ![]() . Используя эти
допущения, точное разделение дифракционных порядков n и (n
+ 1) возможно, если
выполняется следующее условие:
. Используя эти
допущения, точное разделение дифракционных порядков n и (n
+ 1) возможно, если
выполняется следующее условие:
Для симметричного случая выражение (31) принимает вид
Полученное выражение (32) является достаточно общим условием для установления связи между рельефом трехмерного объекта и топологией схемы формирования кодированного изображения.
Из анализа выражения (32) можно сделать следующие выводы:
- чтобы достичь большего ограничивающего угла ![]() , период решетки
, период решетки ![]() должен быть мал по сравнению с величиной
дефекта D функции рельефа
должен быть мал по сравнению с величиной
дефекта D функции рельефа ![]() ; в противном
случае обнаружение дефекта будет невозможно;
; в противном
случае обнаружение дефекта будет невозможно;
- ограничивающий угол ![]() связан с
дифракционным порядком n.
Так, для n=1 и
связан с
дифракционным порядком n.
Так, для n=1 и ![]() обнаружение дефекта
возможно при
обнаружение дефекта
возможно при ![]() . Ясно, что оптическая фильтрация накладывает определенные
ограничения на форму объекта. Ограничения усиливаются по мере увеличения угла
визирования
. Ясно, что оптическая фильтрация накладывает определенные
ограничения на форму объекта. Ограничения усиливаются по мере увеличения угла
визирования ![]() . Но, поскольку чувствительность метода связана с углом
визирования
. Но, поскольку чувствительность метода связана с углом
визирования ![]() , то для каждого отдельного случая можно найти компромисс
между условиями (25) и (32).
, то для каждого отдельного случая можно найти компромисс
между условиями (25) и (32).