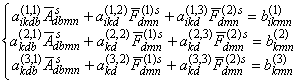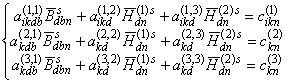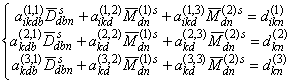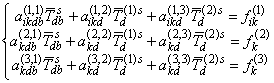УДК 539.3; 537.8
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТОУПРУГИХ СВОЙСТВ ПЬЕЗОАКТИВНЫХ КОМПОЗИТОВ
А.
А. Паньков
Пермский национальный исследовательский политехнический университет
Статья поступила в редакцию 7 апреля 2016 г.
Аннотация. Разработаны математические двухуровневые структурные модели электромагнитоупругости композитов с учетом связанностей деформационных, электрических и магнитных полей. Представлены результаты прогнозирования 21-й независимой константы эффективных трансверсально-изотропных пьезоэлектромагнитоупругих свойств однонаправленного волокнистого композита PVF/феррит на основе решения связанной краевой задачи электромагнитоупругости; использованы новые решения для сингулярных составляющих вторых производных функций Грина для однородной трансверсально-изотропной пьезоэлектромагнитной среды.
Ключевые слова: пьезокомпозит, краевая задача электромагнитоупругости, эффективные свойства.
Abstract. Mathematical two-level structural models of electromagnetoelasticity of composites taking into account coherences of deformation, electric and magnetic fields are developed. Results of prediction of the 21 independent constant of effective transversal-isotropic piezoelectromagnetoelastic properties of the unidirectional fibrous composite PVF/ferrite are presented on the basis of the solution of the boundary-value problem of electromagnetoelasticity; new decisions for singular components of the second derivative Green functions for homogeneous transversal-isotropic piezoelectromagnetoelastic medium are used.
Key words: piezocomposite, boundary-value problem of electromagnetoelasticity, effective properties.
Введение
Разработка новых пьезоактивных пироэлектромагнитных материалов и создание устройств на их основе ‑ активно развивающееся направление материаловедения [1, 2]; композиты находят применение в тех случаях, когда традиционные материалы: кристаллы, керамики, сплавы не обеспечивают необходимого комплекса физико-механических характеристик. Поведение и свойства пьезокомпозитов обуславливаются сложным взаимодействием посредством взаимосвязанных деформационных, электрических и магнитных полей большого числа образующих структуру материала элементов [3‑7]. Возможность оптимизации и управления структурой композитов открывает путь создания новых пьезоматериалов с наперед заданными свойствами. В результате взаимодействия на микроуровне пьезоактивных элементов структуры на макроуровне композита возникают качественно новые эффекты по сравнению с однородными материалами, в частности, проявляются эффекты магнитоэлектрической, пироэлектрической и пиромагнитной связанностей, отсутствующие у входящих в композит однородных фаз [8‑11].
Цель работы – изучение эффекта электромагнитной связанности и комплексный анализ эффективных трансверсально-изотропных пьезоэлектромагнитоупругих свойств однонаправленного волокнистого композита PVF/феррит с различными полидисперсными структурами [4, 7, 11].
1. Микро и макроуровни
Рассматриваем двухфазные пьезоактивные среды в
представительной области ![]() , определяющие
соотношения для фаз
, определяющие
соотношения для фаз ![]() [1,
2, 5]
[1,
2, 5]
![]() ,
,
![]() , (1)
, (1)
![]() ,
,
связывают напряжения ![]() ,
индукции электрического
,
индукции электрического ![]() и магнитного
и магнитного ![]() полей с деформациями
полей с деформациями ![]() , напряженностями электрического
, напряженностями электрического ![]() и магнитного
и магнитного ![]() полей,
температурой однородного внешнего нагрева
полей,
температурой однородного внешнего нагрева ![]() через
считающиеся известными для каждой фазы
через
считающиеся известными для каждой фазы ![]() тензоры
упругих свойств
тензоры
упругих свойств ![]() , пьезоэлектрических
, пьезоэлектрических ![]() и пьезомагнитных
и пьезомагнитных ![]() свойств,
диэлектрических
свойств,
диэлектрических ![]() и магнитных
и магнитных ![]() проницаемостей, температурных
коэффициентов
проницаемостей, температурных
коэффициентов ![]() , пироэлектрических
, пироэлектрических ![]() и пиромагнитных
и пиромагнитных ![]() постоянных.
Выполняются условия идеального контакта на межфазных поверхностях: непрерывность
векторов перемещений, напряжений, индукций электрического и магнитного полей.
постоянных.
Выполняются условия идеального контакта на межфазных поверхностях: непрерывность
векторов перемещений, напряжений, индукций электрического и магнитного полей.
Тензоры ![]() , …,
, …, ![]() эффективных свойств входят в определяющие
соотношения на макроуровне композита
эффективных свойств входят в определяющие
соотношения на макроуровне композита
![]() ,
,
![]() ,
(2)
,
(2)
![]()
и связывают осредненные или
макроскопические значения напряжений ![]() ,
деформаций
,
деформаций ![]() ,
индукций
,
индукций ![]() ,
,
![]() , напряженностей
, напряженностей ![]() ,
, ![]() электрического и
магнитного полей соответственно;
электрического и
магнитного полей соответственно; ![]() ‑
оператор осреднения по области
‑
оператор осреднения по области ![]() структурных
полей.
структурных
полей.
Ненулевые компоненты
рассматриваемых трансверсально-изотропных тензоров ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() на структурном (1) и на макроуровне (2) композита
можно наглядно представить в матричной форме записи
на структурном (1) и на макроуровне (2) композита
можно наглядно представить в матричной форме записи
 ,
,
 ,
, 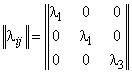 ,
,
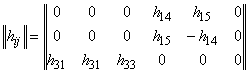 ,
, 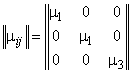 ,
,
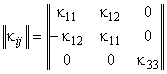 ,
, 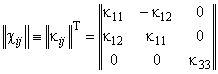 ,
,
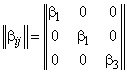 ,
, 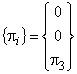 ,
, 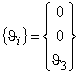 ,
,
где ![]() , тензорные и
матричные индексы связаны между собой соотношениями:
, тензорные и
матричные индексы связаны между собой соотношениями: ![]() ,
,
![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() .
.
2. Обобщенное сингулярное приближение
Решение для тензоров эффективных
упругих свойств ![]() ,
диэлектрической
,
диэлектрической ![]() и
магнитной
и
магнитной ![]() проницаемостей,
пьезомеханических свойств
проницаемостей,
пьезомеханических свойств ![]() и
и
![]() , коэффициентов
электромагнитной связи
, коэффициентов
электромагнитной связи ![]() ,
,
![]() и температурных
напряжений
и температурных
напряжений ![]() ,
вектора эффективных пироэлектрических
,
вектора эффективных пироэлектрических ![]() и
пиромагнитных
и
пиромагнитных ![]() постоянных
в определяющих соотношениях (2) на макроуровне композита в обобщенном
сингулярном приближении [6, 7, 9]
постоянных
в определяющих соотношениях (2) на макроуровне композита в обобщенном
сингулярном приближении [6, 7, 9]
![]() ,
,
![]() ,
,
![]() ,
,
![]() , (3)
, (3)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
получим через поправки к
соответствующим осредненным по области ![]() значениям:
значениям:
![]() , …,
, …, ![]() ,
тензоры разностей:
,
тензоры разностей: ![]() ,
, ![]() ,…,
,…, ![]() ;
; ![]() ‑
относительное объемное содержание 1-й фазы в
‑
относительное объемное содержание 1-й фазы в ![]() ;
например,
;
например, ![]() , где
, где ![]() .
Компоненты тензоров
.
Компоненты тензоров ![]() ,
, ![]() , …,
, …, ![]() в (3) находим из решения систем алгебраических
уравнений [7]
в (3) находим из решения систем алгебраических
уравнений [7]
где коэффициенты
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() , (8)
, (8)
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
правые части для 1-й системы уравнений (4)
![]() , (9)
, (9)
![]() ,
,
![]() ,
,
![]() ,
(10)
,
(10)
![]() ,
,
![]() ,
,
![]() ,
(11)
,
(11)
![]() ,
,
и для 4-й системы (7)
![]() ,
,
![]() , (12)
, (12)
![]() ;
;
в (8) – (12) нижние индексы в круглых
скобках ![]() обозначают [6] выделение симметричной
составляющей по этой паре индексов, тензоры разностей
обозначают [6] выделение симметричной
составляющей по этой паре индексов, тензоры разностей
В формулы (8) ‑ (12) входит
новое решение для матрицы тензоров сингулярных
составляющих ![]() вторых производных функций Грина
вторых производных функций Грина ![]()
![]() ,
(14)
,
(14)
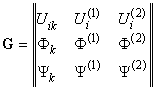 ,
,
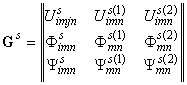
для однородной анизотропной пьезоэлектромагнитной
«среды сравнения» [6], свойства которой заданы через тензоры: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (13), функция Грина
(13), функция Грина ![]() ,
, ![]() ‑ дельта-функция
Дирака,
‑ дельта-функция
Дирака, ![]() , в точке
, в точке ![]() действует единичная
объемная сила, или электрический или магнитный источник,
действует единичная
объемная сила, или электрический или магнитный источник, ![]() ‑ оператор
дифференцирования по координатам вектора
‑ оператор
дифференцирования по координатам вектора ![]() .
Компоненты матрицы
.
Компоненты матрицы ![]() в
(14) вычисляются по формулам
в
(14) вычисляются по формулам
![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
,
![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
,
где оператор
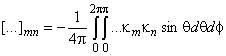
действует на компоненты тензоров
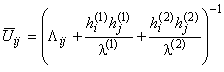 ,
, 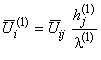 ,
, 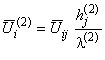 ,
,
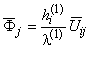 ,
, 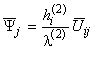 ,
, 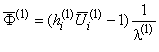 ,
, 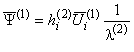 ,
,
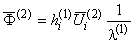 ,
, 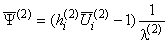 ,
,
в которых использованы обозначения
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
(15)
,
(15)
![]() ,
, ![]() ,
, ![]() ,
,
![]() и
и ![]() ‑ полярные углы в сферической
системе координат, поверхность эллипсоидального «зерна неоднородности» [6]
задана равенством
‑ полярные углы в сферической
системе координат, поверхность эллипсоидального «зерна неоднородности» [6]
задана равенством
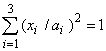 (16)
(16)
через значения главных полуосей ![]() в (9),
в (9), ![]() –
координаты вектора
–
координаты вектора ![]() .
.
3. Волокнистый композит PVF/феррит
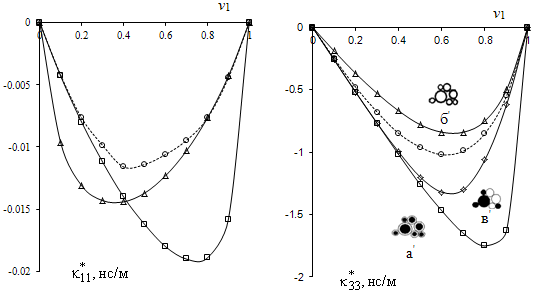
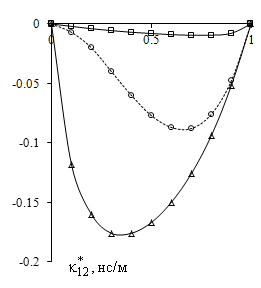
На рис.1 представлены результаты
расчета эффективных коэффициентов электромагнитной связанности ![]() ,
, ![]() и
и ![]() (3) трансверсально-изотропного
волокнистого пьезоэлектромагнетика: пьезоэлектрическая матрица PVF [5, 12] с однонаправленными вдоль оси
(3) трансверсально-изотропного
волокнистого пьезоэлектромагнетика: пьезоэлектрическая матрица PVF [5, 12] с однонаправленными вдоль оси
![]() ферритовыми [5] волокнами
(
ферритовыми [5] волокнами
(![]() ,
, ![]() , (16) с объемной долей
, (16) с объемной долей ![]() . Расчет (рис.1) проведен в обобщенном
сингулярном приближении (3) – (16) для четырех различных случаев выбора свойств
среды сравнения (13), (15): в первом случае (
. Расчет (рис.1) проведен в обобщенном
сингулярном приближении (3) – (16) для четырех различных случаев выбора свойств
среды сравнения (13), (15): в первом случае (![]() ), свойства среды сравнения приравнены
свойствам 1-й фазы
), свойства среды сравнения приравнены
свойствам 1-й фазы
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (17)
, (17)
во втором случае (![]() ) – свойствам 2-й
фазы
) – свойствам 2-й
фазы
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (18)
, (18)
в третьем случае (![]() ) – осредненным по
области
) – осредненным по
области ![]() композита значениям
композита значениям
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (19)
, (19)
и в четвертом случае (![]() ) – искомым
эффективным свойствам композита («схема самосогласования» [6])
) – искомым
эффективным свойствам композита («схема самосогласования» [6])
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (20)
, (20)
решения (![]() ), (
), (![]() ) инвариантны к инверсии
свойств фаз.
) инвариантны к инверсии
свойств фаз.
Результаты расчета (![]() ) и (
) и (![]() ) для эффективных
констант
) для эффективных
констант ![]() ,
, ![]() (рис.1,а,б)
в обобщенном сингулярном приближении в точности совпали с аналитическими
решениями [8] для полидисперсных структур (рис.1,а', рис.1,б');
решение (
(рис.1,а,б)
в обобщенном сингулярном приближении в точности совпали с аналитическими
решениями [8] для полидисперсных структур (рис.1,а', рис.1,б');
решение (![]() )
по схеме самосогласования для
)
по схеме самосогласования для ![]() в точности
совпало с аналитическим решением [11] для полидисперсной структуры на рис.1,в'.
Решения (
в точности
совпало с аналитическим решением [11] для полидисперсной структуры на рис.1,в'.
Решения (![]() ),
(
),
(![]() ) при
«малых» степенях наполнения
) при
«малых» степенях наполнения ![]() близки к решению (
близки к решению (![]() ) для матричной
по 2-й фазе структуре (рис.1,а') и при «больших»
) для матричной
по 2-й фазе структуре (рис.1,а') и при «больших» ![]() ‑
к решению (
‑
к решению (![]() ) для матричной по 1-й фазе структуре (рис.1,б').
Отметим, что решение
) для матричной по 1-й фазе структуре (рис.1,б').
Отметим, что решение ![]() (
(![]() ) также в точности
совпало с решением асимптотического метода осреднения [8] для идеальной
периодической волокнистой структуры. Дополнительно на рис.2 – рис.5
представлены результаты расчета в обобщенном сингулярном приближении
эффективных констант: модулей Юнга
) также в точности
совпало с решением асимптотического метода осреднения [8] для идеальной
периодической волокнистой структуры. Дополнительно на рис.2 – рис.5
представлены результаты расчета в обобщенном сингулярном приближении
эффективных констант: модулей Юнга ![]() ,
, ![]() ,
коэффициентов Пуассона
,
коэффициентов Пуассона ![]() ,
, ![]() ,
модулей сдвига
,
модулей сдвига ![]() ,
, ![]() ,
объемного модуля плоской деформации
,
объемного модуля плоской деформации ![]() (рис.2), электромеханических
(рис.2), электромеханических
![]() ,
,
![]() ,
,
![]() (рис.3)
и магнитомеханических
(рис.3)
и магнитомеханических ![]() ,
, ![]() ,
,
![]() ,
,
![]() (рис.4)
констант, диэлектрических
(рис.4)
констант, диэлектрических ![]() ,
, ![]() и
магнитных
и
магнитных ![]() ,
, ![]() проницаемостей
(рис.5) волокнистого пьезоэлектромагнетика в зависимости от объемной доли
феррита.
проницаемостей
(рис.5) волокнистого пьезоэлектромагнетика в зависимости от объемной доли
феррита.
|
а б |
|
|
в |
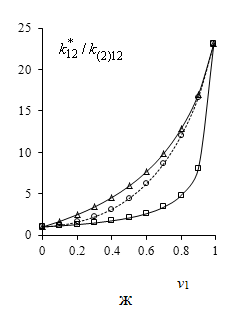
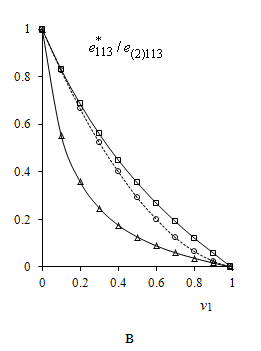
Рис.1 Эффективные коэффициенты
электромагнитной связанности
|
|
|
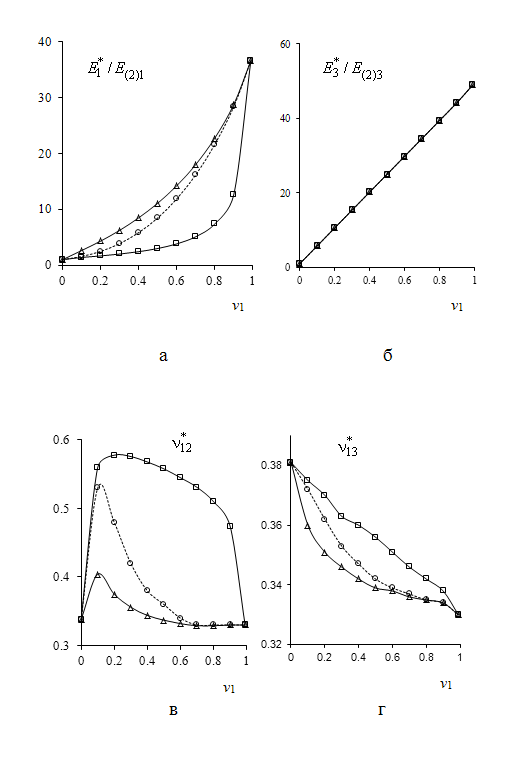
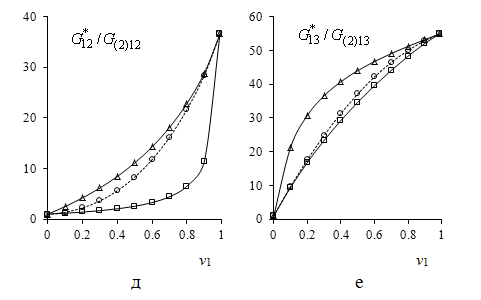
Рис.2
Эффективные модули упругости: модули Юнга |
|
|
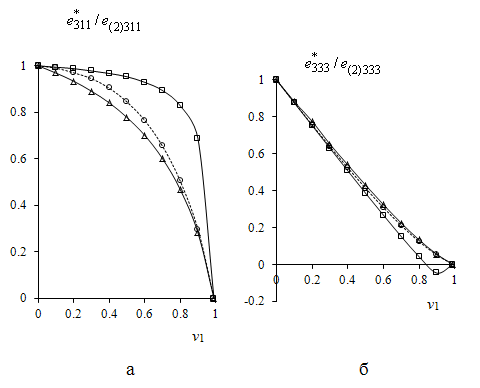
Рис.3
Эффективные электромеханические константы
|
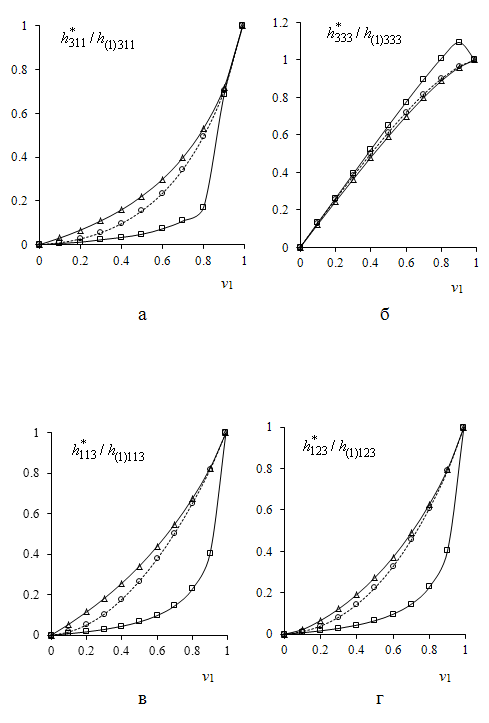
Рис.4
Эффективные магнитомеханические константы ![]() (а),
(а), ![]() (б),
(б), ![]() (в),
(в), ![]() (г)
(г)
пьезоэлектромагнетика с объемной
долей феррита ![]()
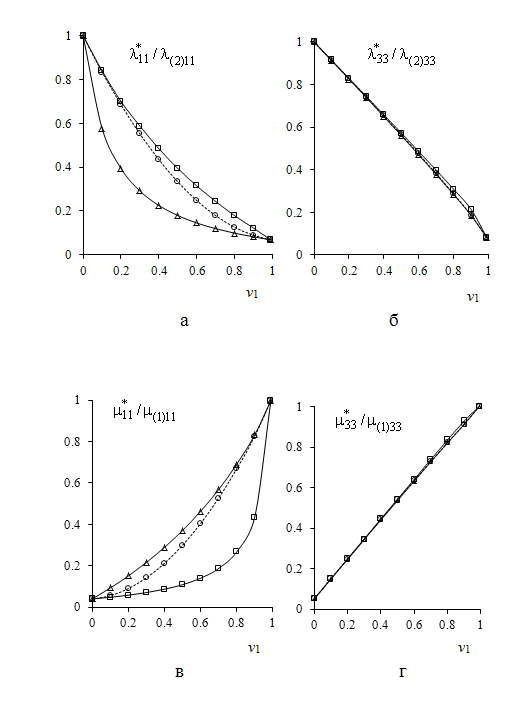
Рис.5
Эффективные диэлектрические ![]() (а),
(а), ![]() (б) и магнитных
(б) и магнитных ![]() (в),
(в),
![]() (г)
(г)
проницаемости пьезоэлектромагнетика с
объемной долей феррита ![]()
Заключение
Разработаны новые математические двухуровневые структурные модели электромагнитоупругости композитов с учетом связанностей деформационных, электрических и магнитных полей. Получены решения связанных краевых задач электромагнитоупругости в обобщенном сингулярном приближении статистической механики композитов на основе новых решений для сингулярных составляющих вторых производных функций Грина для однородной трансверсально-изотропной пьезоэлектромагнитной среды с эллипсоидальным зерном неоднородности. Представлены результаты прогнозирования 21-й независимой константы эффективных трансверсально-изотропных упругих и пьезоэлектромагнитных свойств однонаправленного волокнистого композита: пьезоэлектрика PVF с ферритовыми волокнами в обобщенном сингулярном приближении решения связанной краевой задачи электромагнитоупругости. Выявлен существенно немонотонный характер изменения эффективных коэффициентов электромагнитной связанности композита PVF/феррит от величины наполнения волокнами; определены значения объемных долей волокон, при которых эти коэффициенты принимают экстремальные значения. Для частных случаев проведены сравнения с известными аналитическими решениями асимптотического метода осреднения [8] для идеальной периодической волокнистой структуры, решениями на составных ячейках и на основе «схемы самосогласования» для различных полидисперсных структур (рис.1, а' ‑ в') [4, 11].
Работа выполнена при финансовой поддержке гранта РФФИ № 14-01-96004 р_урал_а.
Литература
1. Мэзон У. Пьезоэлектрические кристаллы и их применения в ультраакустике. ‑ М.: Изд-во иностр. лит., 1952. ‑ 448 с.
2. Партон В.З., Кудрявцев Б.А. Электромагнитоупругость пьезоэлектрических и электропроводных тел. М.: Наука, 1988. ‑ 471 с.
3. Волков С.Д. Статистическая механика композитных материалов / С.Д. Волков, В.П. Ставров. – Минск: Изд-во Белорус. гос. ун-та, 1978. – 208 с.
4. Кристенсен Р. Введение в механику композитов. – М.: Мир, 1982. – 334 с.
5. Хорошун Л.П., Маслов Б.П., Лещенко П.В. Прогнозирование эффективных свойств пьезоактивных композитных материалов. – Киев: Наук. думка, 1989. – 208 с.
6. Шеpмеpгоp Т.Д. Теоpия упpугости микpонеодноpодных сpед. ‑ М.: Наука, 1976. ‑ 399 с.
7. Паньков А.А. Статистическая механика пьезокомпозитов. ‑ Пермь: Изд-во Перм. гос. техн. ун-та, 2009. ‑ 480 с.
8. Гетман И.П. О магнитоэлектрическом эффекте в пьезокомпозитах // ДАН СССР. ‑ 1991. ‑ Т. 317. ‑ № 2. – С. 341-343
9. Паньков А.А. Влияние разупорядоченности и инверсии фаз на электромагнитную связанность пьезокомпозита с квазипериодической структурой // Журнал радиоэлектроники: электронный журнал. 2014. ‑ №1; URL: http://jre.cplire.ru/jre/jan14/12/text.pdf
10. Паньков А.А. Диэлектрическая релаксация в волокнистом композите полиэтилен/феррит // Журнал радиоэлектроники: электронный журнал. 2014. ‑ №2; URL: http://jre.cplire.ru/jre/feb14/1/text.pdf
11. Pan’kov A.A. Self-consistent solutions for electromagnetic coupling coefficients of fibrous piezocomposite // Composites: Mechanics, Computations, Applications. An International Journal. ‑ 2014. ‑ Vol. 5. ‑ No 1. ‑ P.77-88
12. Sessler G.M. Piezoelectricity in polyvinylidenefluoride // J. Acoust. Soc. Amer.. – 1981. – Vol. 70. – No 6. ‑ P.1596-1608