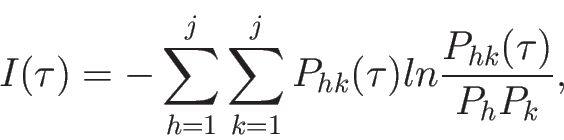В АНАЛИЗЕ ИОНОСФЕРНОГО КАНАЛА СВЯЗИ
Московский государственный университет им. М.В. Ломоносова,
физический факультет
Аннотация.
Представлен последовательный анализ экспериментальных временных рядов,
характеризующих динамику изменения параметров отраженного сигнала на
односкачковой вертикальной ионосферной радиотрассе. Получены оценки значений
корреляционной размерности, спектра показателей Ляпунова для сигнальных
и шумовых компонент. Выполнена реконструкция аттрактора для
слабо возмущенной ионосферы.
Ключевые слова:
распространение радиоволн, ионосферный канал связи, помехи, фазовый портрет, аттрактор.
Abstract.
The dynamics of radio signal propagating through the single-hop vertical
ionospheric path was analyzed using
the experimental time series. Correlation
dimension, Lyapunov exponents spectrum for signal and noise components are
evaluated. Attractor reconstruction for the weakly disturbed ionosphere is carried out.
Key words:
radio wave propagation, ionospheric communications channel, noise, phase surface, attractor.
Введение
Работа ионосферных каналов связи (ИКС) основана на явлении однократного или многократного отражения излучения коротковолнового диапазона от ионосферы. К серьезным недостаткам ИКС можно отнести низкую скорость и слабую помехоустойчивость процесса передачи информации, обусловленные нестационарностью ионосферы. Флуктуации параметров радиоканала требуют решения многопараметрической задачи определения количества мод распространения, учета вариаций амплитуд и фаз каждой из них, оценки тонкой пространственно-временной структуры поля в зоне приема и т. д. [1,2,3].
Проведенные в последние годы успешные исследования с позиций теории динамического хаоса позволили установить ряд физических закономерностей, связывающих статистические и фрактальные характеристики среды и регистрируемой волны [4,5,6,7]. Одной из сильных сторон методов нелинейно-динамического описания является прогнозирование свойств физической системы. Как правило, «глубина прогноза» определяется объемом первичной выборки.
Цель данной работы состоит в оценке эффективности применения методов нелинейной динамики для анализа волновых процессов в слабо возмущенном ионосферном канале. Выполнена реконструкция аттрактора системы в фазовом пространстве, оценены основные пространственные (корреляционная размерность) и динамические (максимальный показатель Ляпунова) фрактальные характеристики исследуемой системы.
Методы обработки скалярных временных рядов
Пусть наблюдаемая физическая величина образует скалярный временной ряд значений с
эквидистантным шагом ![]() . Анализ временного ряда позволяет оценить число независимых
переменных, необходимых для описания системы, то есть число «степеней свободы»
или размерность пространства состояний.
В принципе, возможно конструирование модели системы в виде дифференциальных уравнений или
отображений, которая позволяла бы адекватно воспроизвести наблюдаемую временную зависимость и
прогнозировать ее поведение.
. Анализ временного ряда позволяет оценить число независимых
переменных, необходимых для описания системы, то есть число «степеней свободы»
или размерность пространства состояний.
В принципе, возможно конструирование модели системы в виде дифференциальных уравнений или
отображений, которая позволяла бы адекватно воспроизвести наблюдаемую временную зависимость и
прогнозировать ее поведение.
Математической основой для процедуры реконструкции фазовых траекторий служит теорема Такенса [8,9], основанная на операциях вложения множеств. Пусть A есть компактное подмножество N-мерного пространства X. Определим вложение множества A в m-мерное пространство Y как задание отображения X в Y такого, что совпадение образов двух векторов, принадлежащих A, возможно только при равенстве этих векторов. Теорема Такенса утверждает, что любое гладкое отображение X в Y будет задавать вложение множества A в пространство Y при условии, что m > 2DA+1, где DA - фрактальная размерность множества A.
Множество точек последовательности состояний системы в собственных координатах принято называть ее фазовой траекторией. Если поведение системы полностью стохастично, фазовая траектория равномерно заполняет некоторый объем фазового пространства. Если же это детерминированный или динамически хаотичный процесс, траектория заполнит поверхность какой-либо фигуры в многомерном пространстве.
Ряд методик [4] позволяет восстановить параметры динамической системы по единственной
реализации процесса путем изучения траектории системы в фазовом пространстве, координатами
которого являются компоненты вектора
![]() .
Временной шаг
.
Временной шаг ![]() принято называть интервалом задержки, а m - вложенной размерностью выборки.
Данная операция называется «погружением аттрактора» в пространство размерности m.
Результатом успешного погружения является выявление определенных закономерностей в поведении
траектории системы в пространстве данной размерности. Существует несколько способов отбора
параметров реконструкции, но ни один не дает однозначного ответа [5].
принято называть интервалом задержки, а m - вложенной размерностью выборки.
Данная операция называется «погружением аттрактора» в пространство размерности m.
Результатом успешного погружения является выявление определенных закономерностей в поведении
траектории системы в пространстве данной размерности. Существует несколько способов отбора
параметров реконструкции, но ни один не дает однозначного ответа [5].
Для выбора оптимального интервала задержки была использована методика, разработанная
Фразером и Свинни [10]. Она основана на теории информации и предлагает использовать
значение первого локального минимума взаимной информации для xi и ![]() в качестве
интервала задержки. Конечная формула взаимной информации выглядит следующим образом:
в качестве
интервала задержки. Конечная формула взаимной информации выглядит следующим образом:
Выбор оптимальной вложенной размерности производился с помощью метода ложных ближайших соседей
(false nearest neighbours - FNN) [11,12]. Пусть Ph(m) и Pk(m) - два близких соседа
в реконструкции m, а Ph(m+1) и Pk(m+1) соответствующие им векторы в реконструкции
размерности m+1. Для каждой точки в серии вычисляется соотношение:
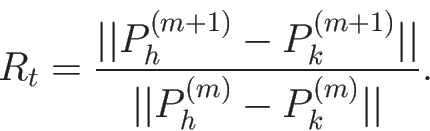 |
(2) |
Одна из основных и самых информативных характеристик хаотических процессов - корреляционная размерность восстановленного аттрактора. Она показывает, насколько сложная система стоит за наблюдаемым процессом. Чем сложнее система, тем больше уравнений требуется для ее описания, тем больше корреляционная размерность, а сам процесс ближе по своим характеристикам к белому шуму. Таким образом, данную величину можно также рассматривать как меру стохастичности процесса.
Введем определение корреляционной суммы для множества точек pi фазового пространства, как отношение
количества пар точек расстояние между которыми не превышает значения ![]() ,
к полному числу пар точек [8]:
,
к полному числу пар точек [8]:
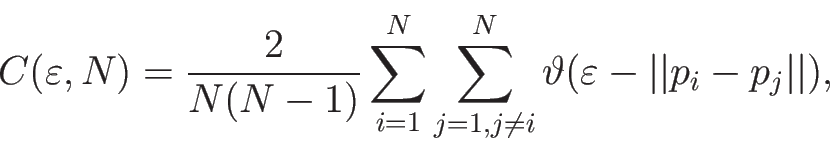 |
(3) |
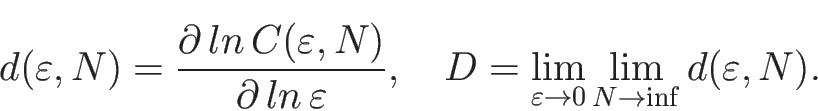 |
(4) |
Для обеспечения достаточной статистики нужно иметь
![]() или
или
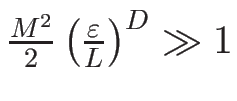 , тогда
, тогда
![]() - максимальная размерность,
которую допустимо оценивать, имея в распоряжении M точек.
Метод главных компонент [13], также известный как метод эффективной размерности, сингулярное
разложение, преобразование Корунена-Лоэва, - является широко используемой техникой для уменьшения
размерности многомерных данных до нескольких главных мод. Результатом измерений будет
временной ряд
- максимальная размерность,
которую допустимо оценивать, имея в распоряжении M точек.
Метод главных компонент [13], также известный как метод эффективной размерности, сингулярное
разложение, преобразование Корунена-Лоэва, - является широко используемой техникой для уменьшения
размерности многомерных данных до нескольких главных мод. Результатом измерений будет
временной ряд ![]() а результатом реконструкции аттрактора
а результатом реконструкции аттрактора ![]() m-мерных векторов.
Поэтому решено использовать простой итерационный алгоритм сингулярного разложения.
К достоинствам этого разложения относятся его простота и возможность почти без изменений перенести
его на данные с пробелами, а также взвешенные данные.
m-мерных векторов.
Поэтому решено использовать простой итерационный алгоритм сингулярного разложения.
К достоинствам этого разложения относятся его простота и возможность почти без изменений перенести
его на данные с пробелами, а также взвешенные данные.
Размерность реконструкции и параметры Ляпунова
Апробация методов реконструкции фазовых траекторий была проведена на экспериментальных сериях,
полученных при вертикальном зондировании ионосферы [14].
Изучалось поведение реальной и мнимой компоненты сигнала с двух скрещенных под прямым
углом антенн ![]() и
и ![]() при длительности выборки не менее 2000 отсчетов.
Для анализа выбирались данные о поведении первой и второй характеристической
волны в отдельности, их смеси, а также шума ИКС.
при длительности выборки не менее 2000 отсчетов.
Для анализа выбирались данные о поведении первой и второй характеристической
волны в отдельности, их смеси, а также шума ИКС.
Для каждого временного ряда проводилась реконструкция в фазовом пространстве и расчет
количественных характеристик в соответствии с описанными методами.
Обработка осуществлялась с использованием пакета программ TISEAN [15,16].
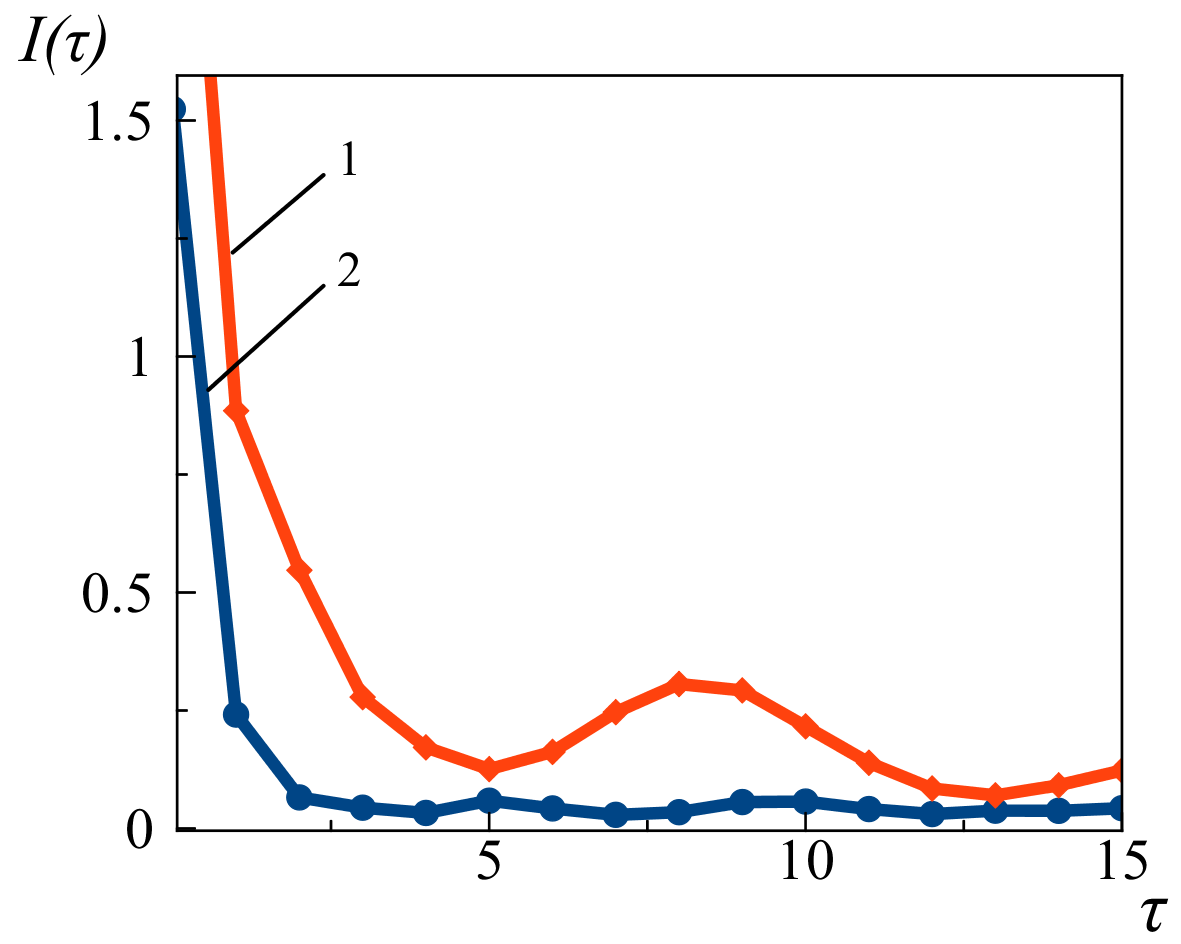
Первый минимум взаимной информации ![]() , задаваемый соотношением (1),
обычно является хорошей оценкой для интервала задержки. Исходя из построенных зависимостей
(рис. 1), можно предположить, что использование единичного лага не будет являться
грубой ошибкой. Такой выбор будет удобным при сравнении параметров сигнала и шума, временная
задержка для которого, как правило, выбирается равной 1.
, задаваемый соотношением (1),
обычно является хорошей оценкой для интервала задержки. Исходя из построенных зависимостей
(рис. 1), можно предположить, что использование единичного лага не будет являться
грубой ошибкой. Такой выбор будет удобным при сравнении параметров сигнала и шума, временная
задержка для которого, как правило, выбирается равной 1.
|
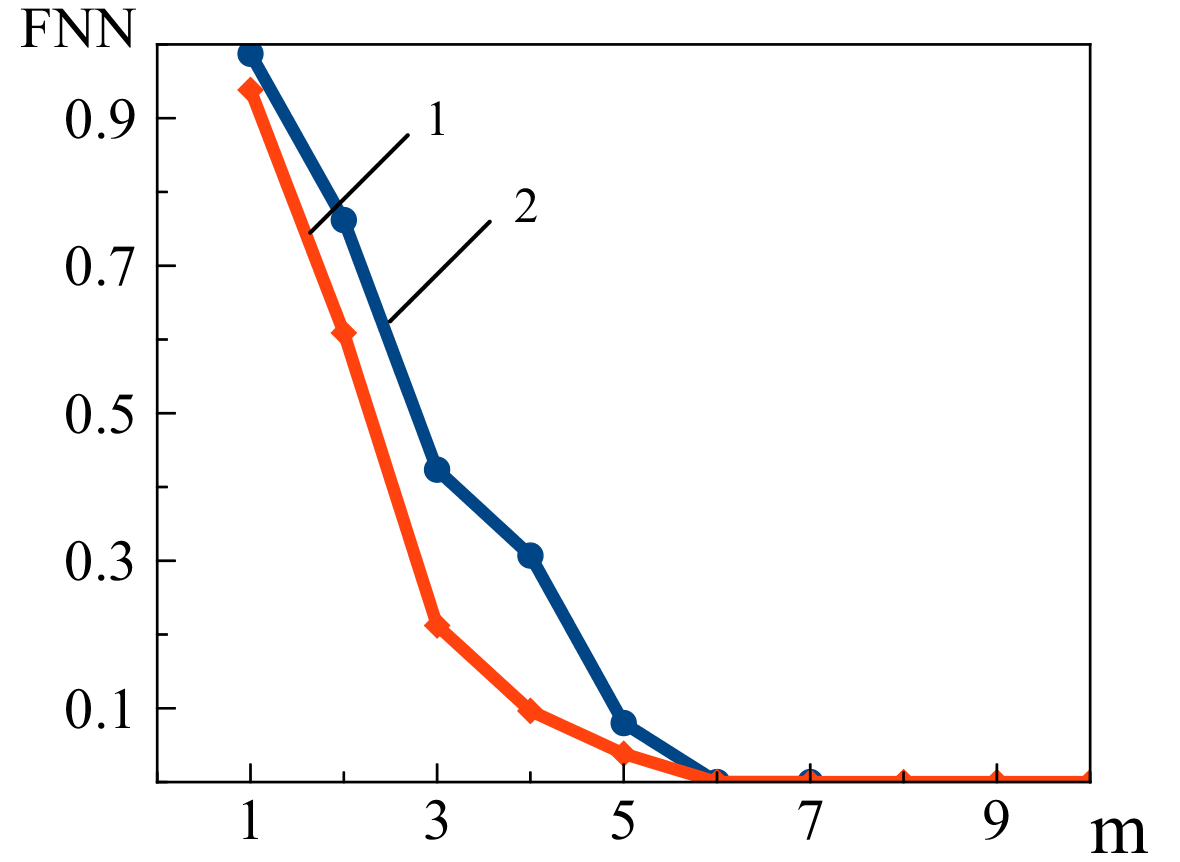
Для определения размерности реконструкции рассчитывалось значение доли ближайших ложных соседей при различных значениях размерности. В результате обработки получены значения для характеристических волн и их смеси m=5, а для остатка, после отделения тренда сигнала и шума, порядка m=5,6 (рис. 2). Вычисление корреляционной размерности D2 можно осуществить в три этапа.
- Определение границы «области измерения» на оси
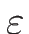 из
графика Раппа - двойной логарифмической зависимости
из
графика Раппа - двойной логарифмической зависимости
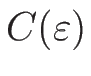 .
.
- Выделение фрагментов, находящихся в данных границах.
- Вычислене средних значений графиков Раппа на этих участках [17].
|
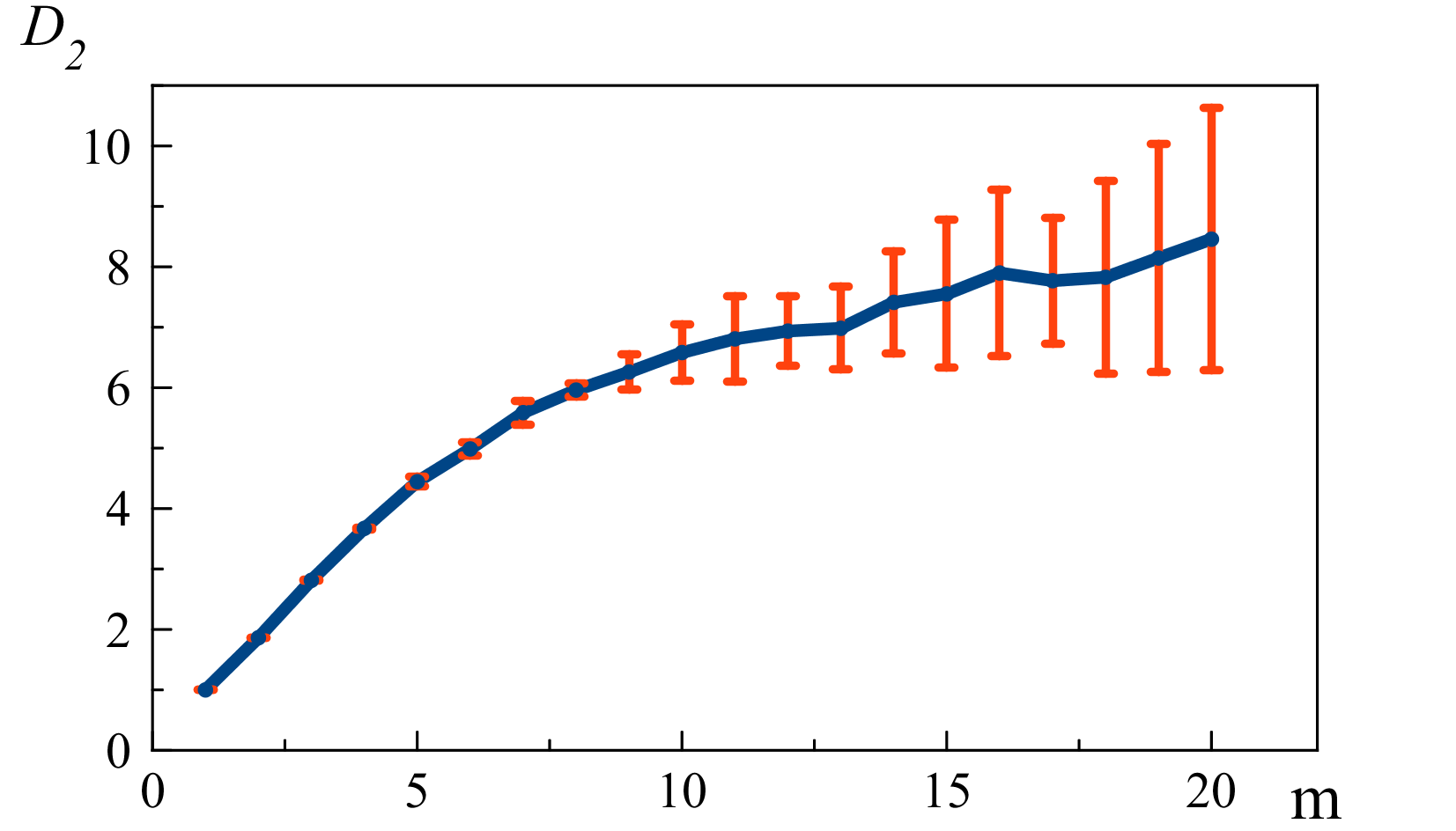
Хорошую оценку размерности лагового пространства m можно получить из анализа
насыщения графика зависимости D2 от m. В случае стохастического процесса
насыщнеия не будет, а сама корреляционная размерность будет равна размерности лагового
пространства m. Для хаотического процесса насыщение наступает при
достижении минимального значения m, необходимого для описания динамики системы.
К тому же при размерности m большей минимальной начинает резко
возрастать погрешность ![]() , что характерно для стохастических процессов.
На рис. 3 представлена зависимость D2(m), демонстрирующая изложенные
выше свойства поведения систем.
, что характерно для стохастических процессов.
На рис. 3 представлена зависимость D2(m), демонстрирующая изложенные
выше свойства поведения систем.
|
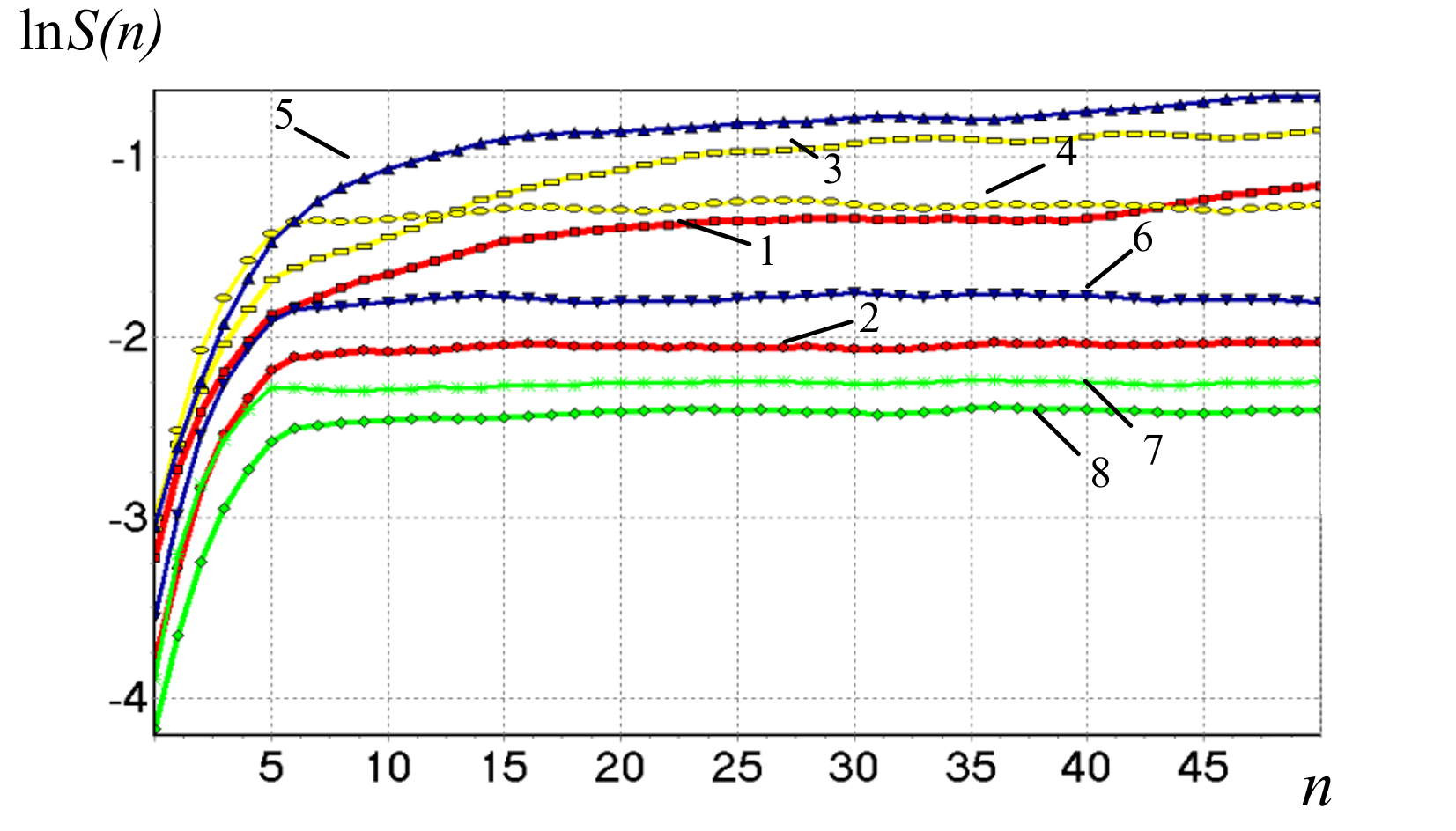
Рассчитанные значения старших показателей Ляпунова [18] для обработанных
рядов лежат в диапазоне от 0,008 до 0,025. При этом для шума они близки к 0,008.
Для остальных временных рядов показатели Ляпунова, принимают значения в области
![]() . На рис. 4 приведена зависимость логарифма коэффициента
разбегания фазовых траекторий от номера итерации (времени) для нескольких временных рядов.
Тангенс угла наклона к этим кривым служит оценкой максимального показателя Ляпунова.
. На рис. 4 приведена зависимость логарифма коэффициента
разбегания фазовых траекторий от номера итерации (времени) для нескольких временных рядов.
Тангенс угла наклона к этим кривым служит оценкой максимального показателя Ляпунова.
«Карты хаоса» и реконструкция аттрактора
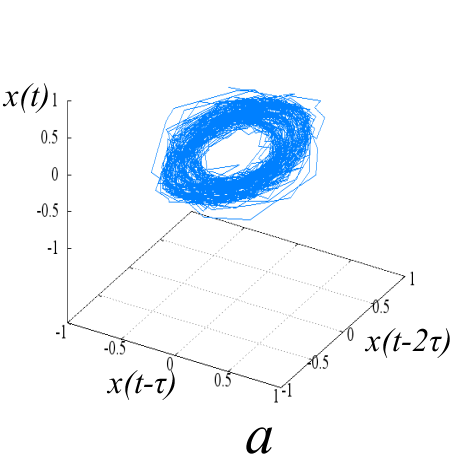
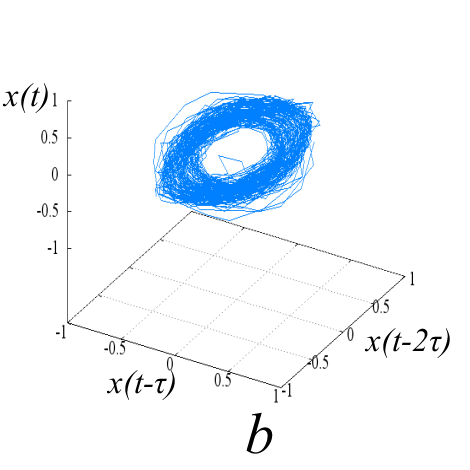
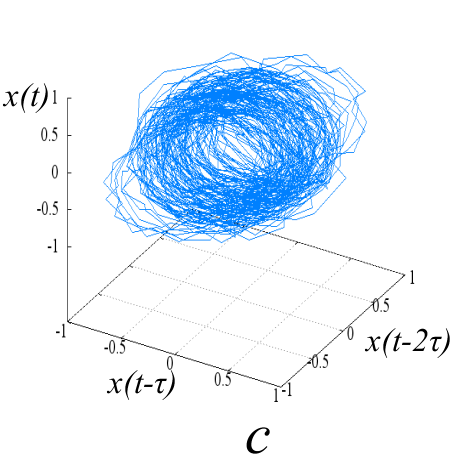
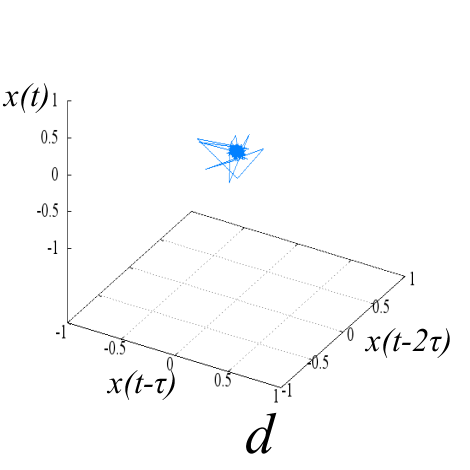
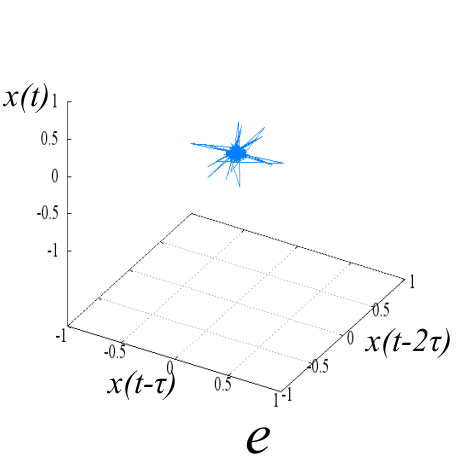
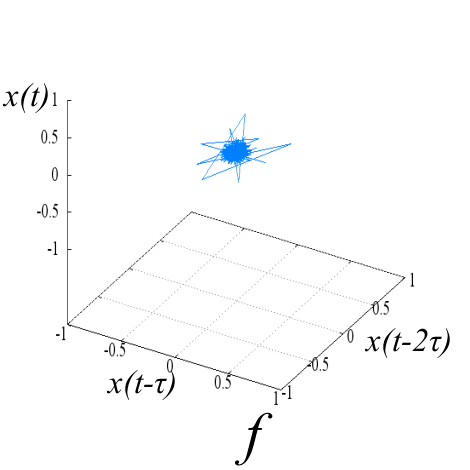
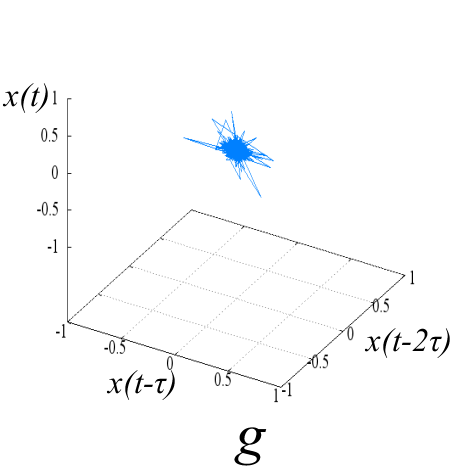
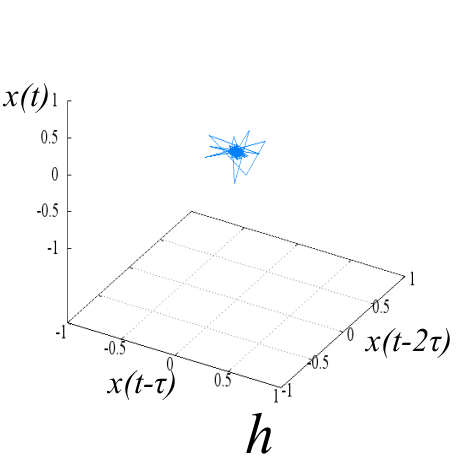
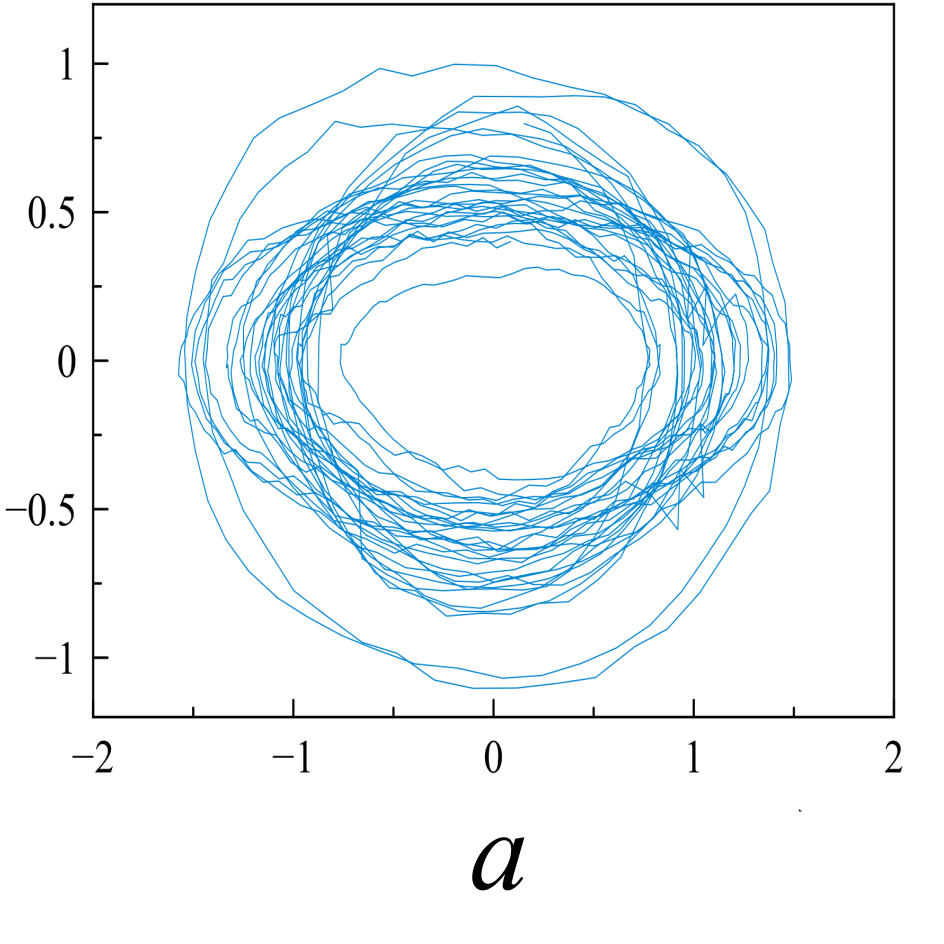
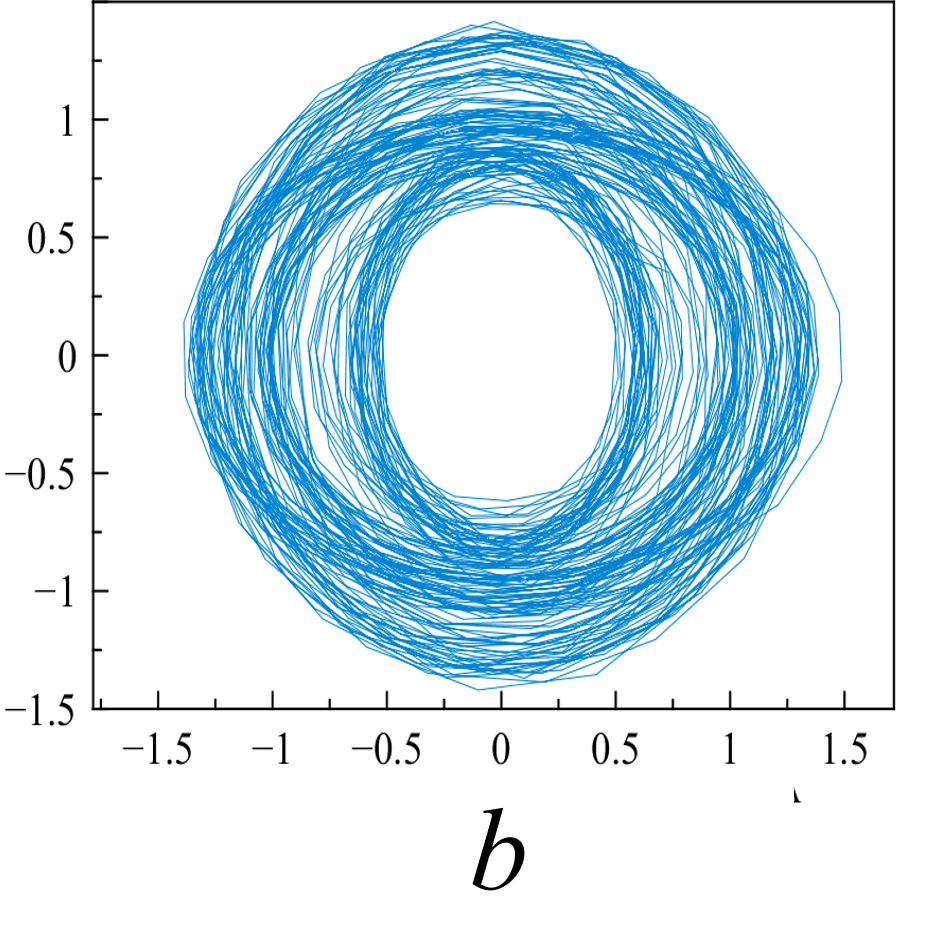
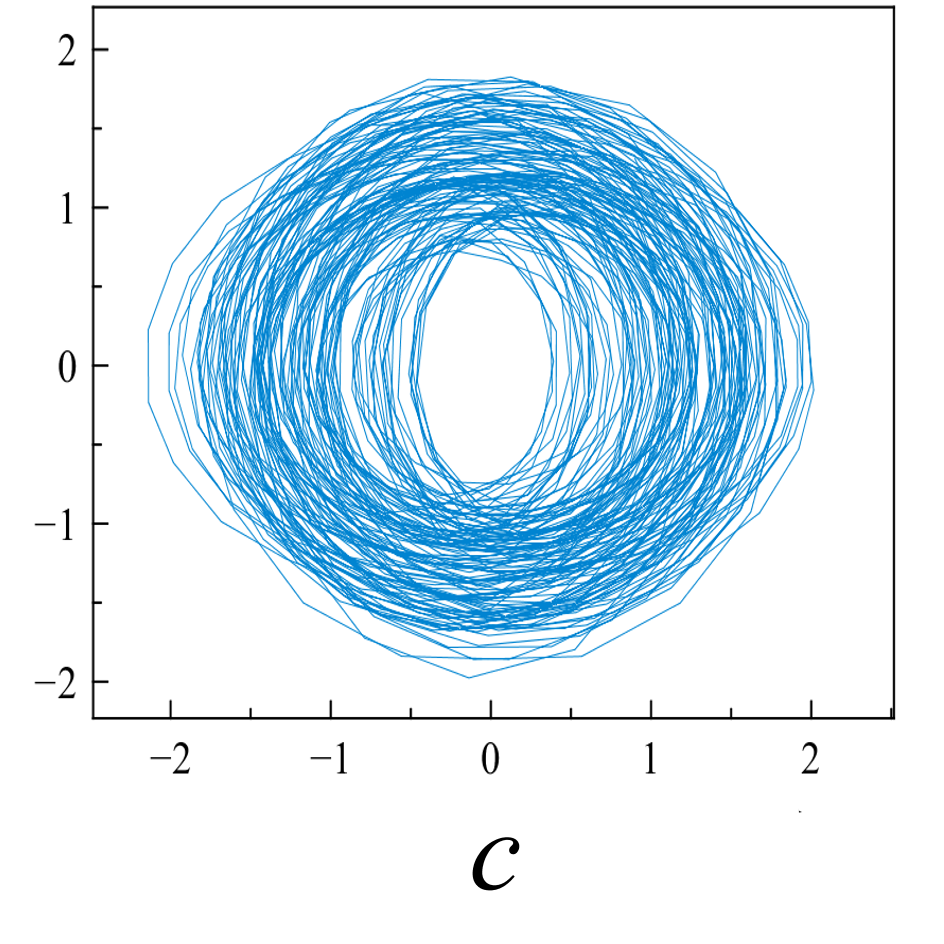
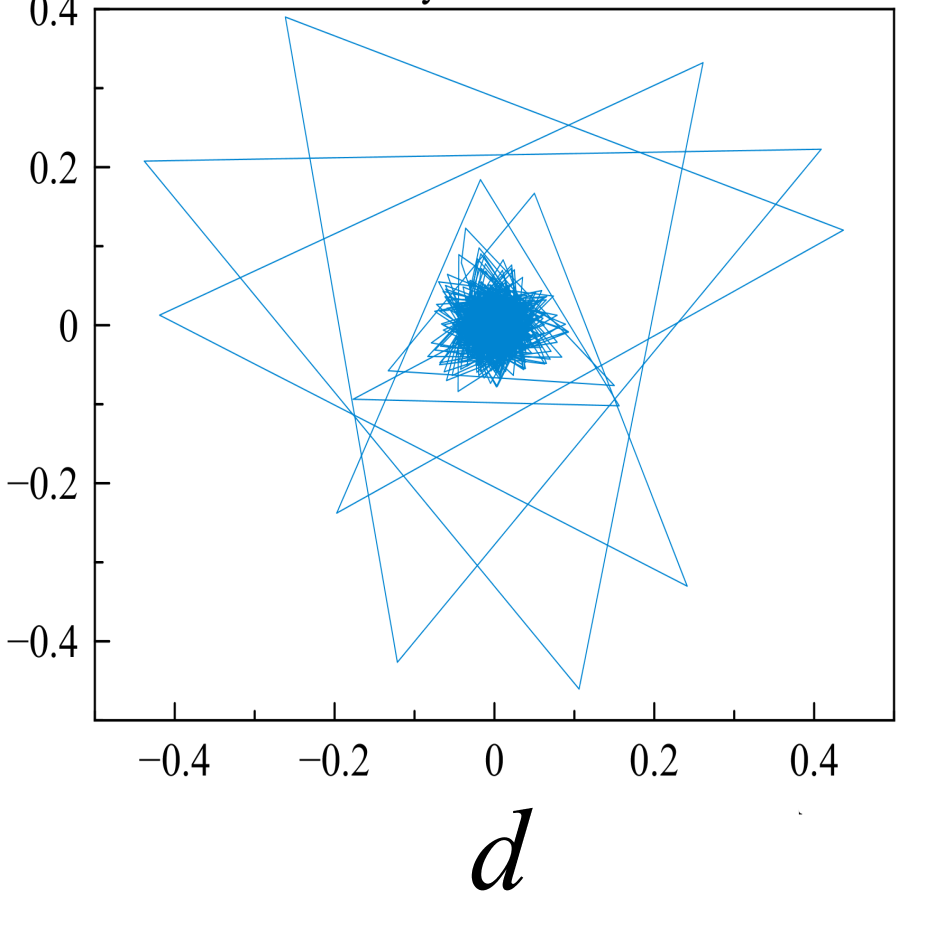
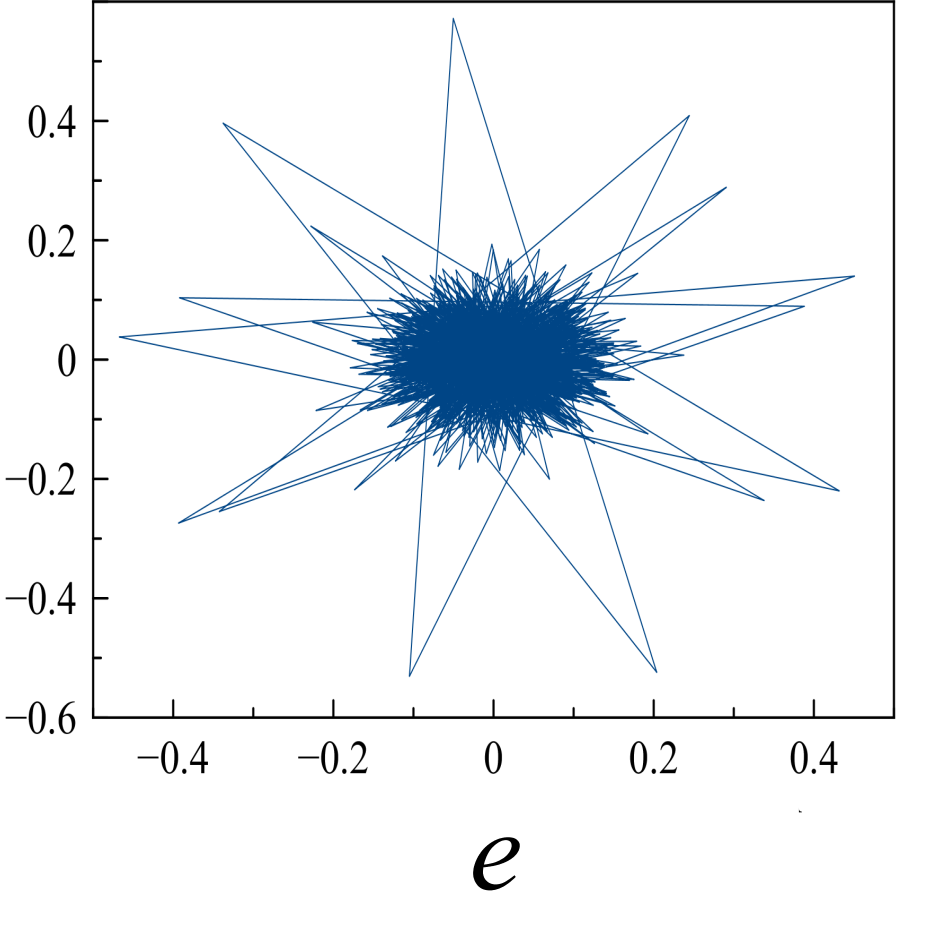
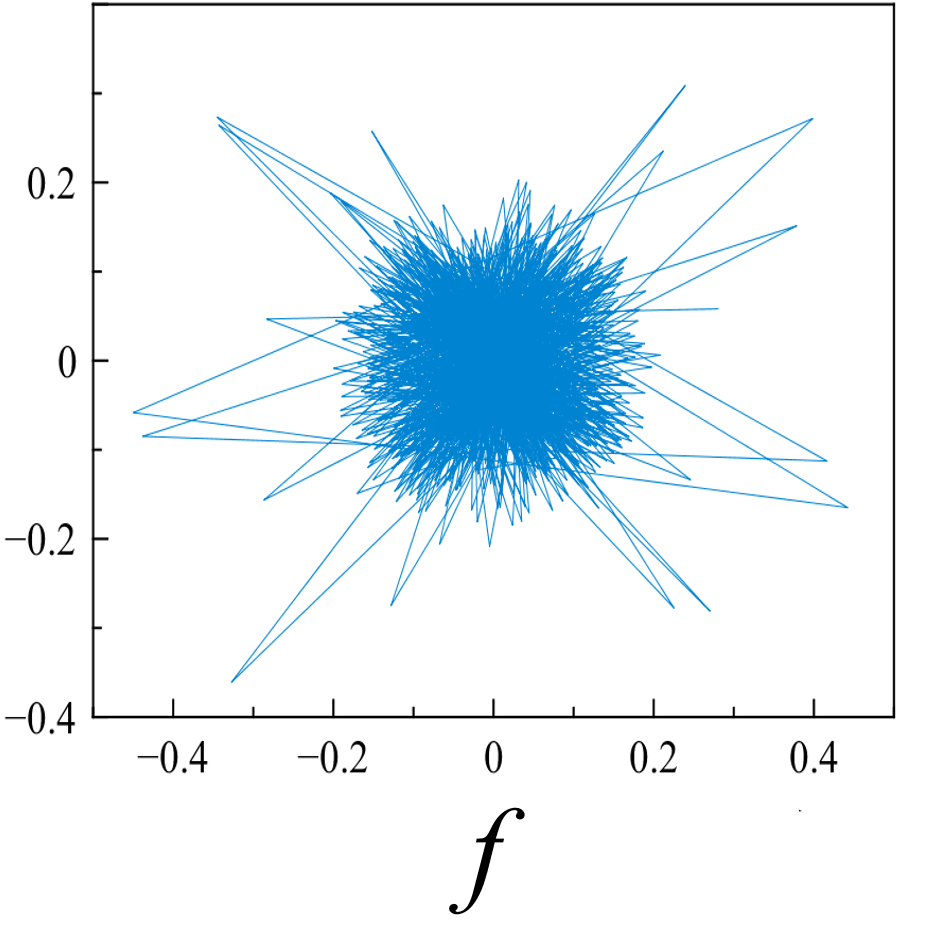
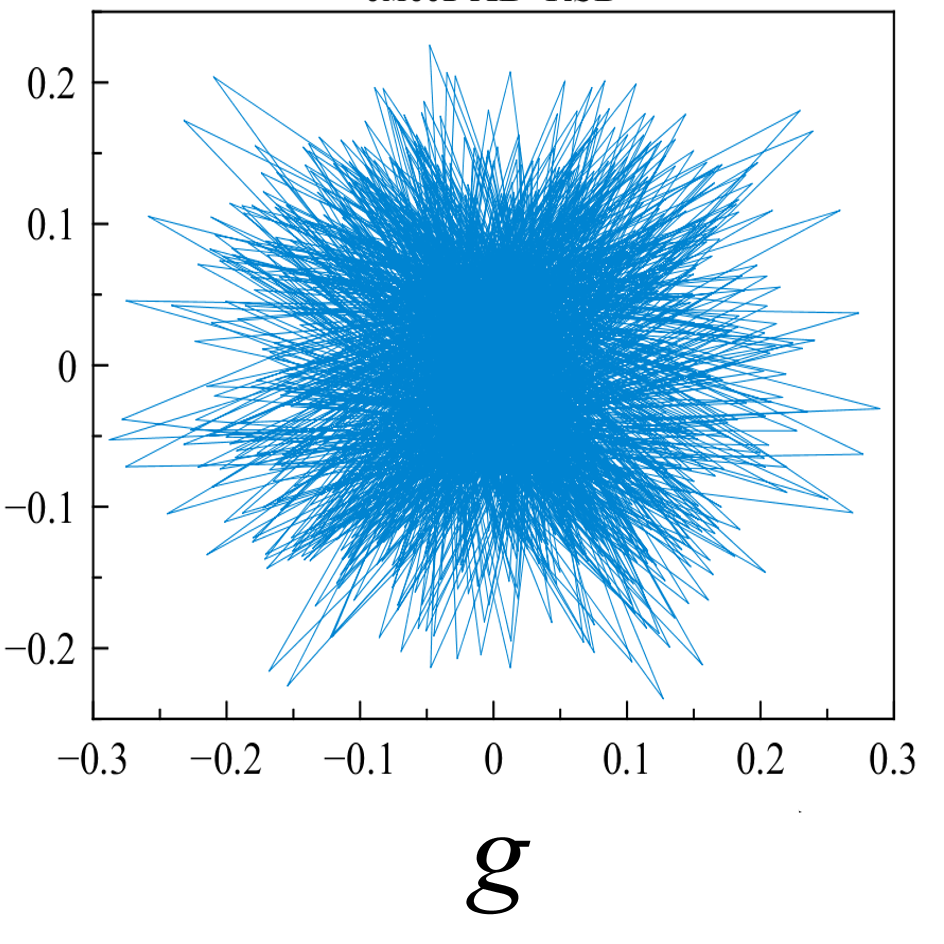
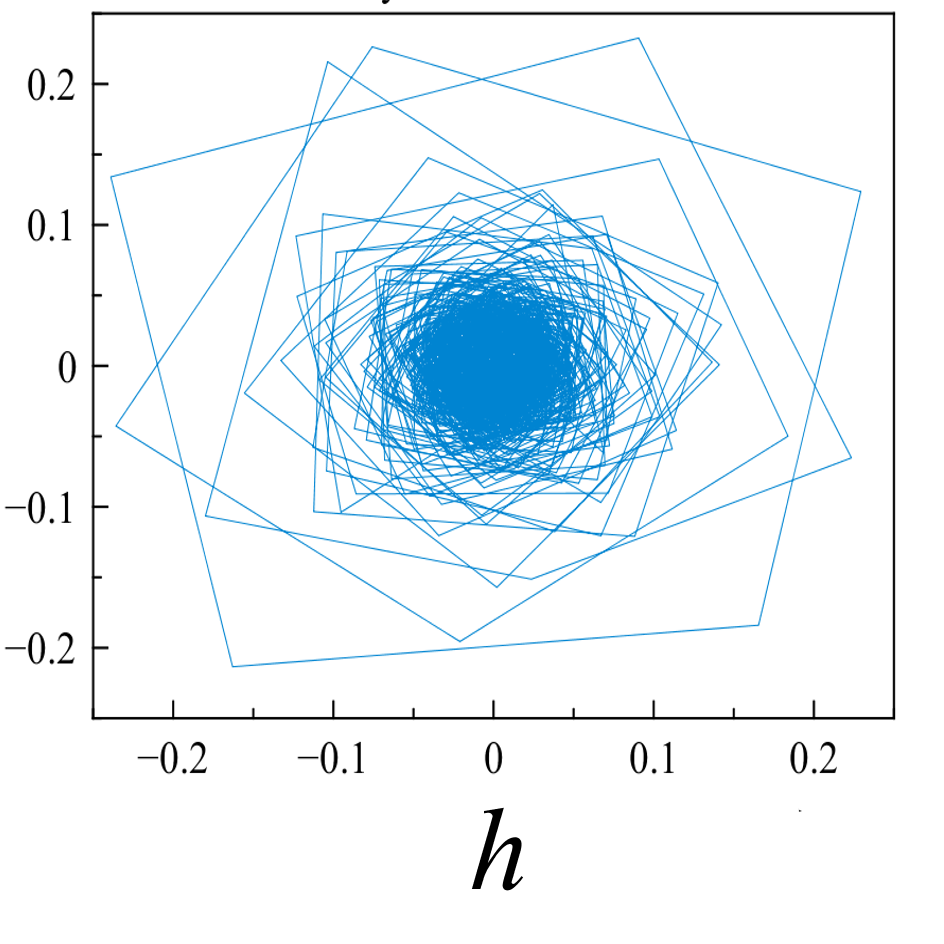
Исследуемые эквидистантные временные ряды соответствуют регистрации отраженного сигнала от слабо возмущенной ионосферы. Отсчеты для каждой из магнитоионных компонент грубо могут быть аппроксимированы гармоникой на соответствующей доплеровской частоте. Для визуализации динамики системы представим экспериментальную выборку в виде трехмерной однопараметрической «карты хаоса» [19] с единичным временным шагом (рис. 5). По виду траекторий на карте можно восстановить тип функционального соотношения xn = f(xn-1, xn-2).
|
Множества траекторий на картах 5a и 5b заполняют кольцо, что соответствует квазигармоническому процессу с глубиной вариации амплитуды, пропорциональной отношению ширины кольца к его внешнему радиусу. Иная структура у карты смешанного сигнала - в выбранной размерности пространства отображения траектории укладываются в эллипсоид вращения с ориентацией и значением полуосей, зависящими от разности доплеровских частот магнитоионных компонент.
Визуализация реконструированного аттрактора рассматриваемого временного ряда после редуцирования размерности пространства, выполненного по методу главных компонент, до значения 2 представлена на рис. 6. Проекции на плоскость, полученные методом главных компонент, строго говоря, не могут быть названы фазовыми портретами, поскольку имеют множественные пересечения траекторий, и противоречат единственности решения системы динамических уравнений для изучаемого процесса. Частично такие пересечения определяются грубостью шага по времени (цикла измерения), частично - недостаточностью размерности выбранного отображения.
|
Представленные реконструкции аттракторов носят качественный характер, но позволяют детектировать «парциальные» структуры в фазовых портретах характеристических волн, - вложенные в окружность пересекающиеся эллипсоиды для первой характеристической волны и вложенные не пересекающиеся эллипсоиды - для второй.
Шум канала в условиях эксперимента (рис 5d, 5h) может быть аппроксимирован как система с бесконечным числом степеней свободы. Соответственно в аттракторах шума невозможно выделение ограниченного набора главных направлений и аттракторы не должны иметь регулярной формы, что хорошо иллюстрируют приведенные рисунки.
Заключение
Рассмотренные методы нелинейной динамики далеко не исчерпывают арсенал математического аппарата реконструкции фазовых траекторий сложных физических процессов. На примере обработки временных рядов, соответствующих однократному отражению импульсных сигналов от слабо возмущенной ионосферы впервые получен ряд характеристик, позволяющих прогнозировать состояние ионосферы и отлаживать на основе прогнозов алгоритмы помехоустойчивого кодирования.
Относительно слабое различие размерности вложения, при которой доля ложных ближайших соседей значимо спадает, для собственно сигнала и его шумовой компоненты (5 и 5,6 соответственно) свидетельствует о динамической детерминированности и параметрической корреляции тренда временного ряда и его шумовой компоненты.
Диапазон значений и положительная определенность максимального показателя Ляпунова как для сигнальной, так и для шумовой компонент позволяют строить долгосрочные (в масштабе длительности используемых экспериментальных выборок) прогнозы эволюции отраженного сигнала, корректно экстраполируя их на значения текущих параметров ионосферы, влияющих на повдение канала связи.
Литература
-
- 1.
- Kenneth Davies. Ionospheric Radio. Institution of Engineering and Technology, 1990.
- 2.
- E. L. Afraimovich, E. A. Kosogorov, O. S. Lesyuta, I. I. Ushakov, and
A. F. Yakovets. Geomagnetic control of the spectrum of traveling ionospheric disturbances
based on data froma global GPS network. Annales Geophysicae, 19(7):723-731, 2001.
- 3.
- V. E. Gherm, N. N. Zernov, and H. J. Strangeways. HF propagation in a
wideband ionospheric fluctuating reflection channel: Physically based software
simulator of the channel. Radio Science, 40(1):RS1001, January 2005.
- 4.
- А.А. Любушин. Анализ данных систем геофизического и экологического
мониторинга. М., Наука, 2008, 228с.
- 5.
- А.А. Потапов. Фракталы в радиофизике и радиолокации: топология
выборки. М., Университетская книга, 2005, 848с.
- 6.
- Т.И. Арсеньян, П.В. Короленко. Оптика случайно-неоднородных сред и
проблемы распространения лазерного излучения в тропосфере. – М.:
Физический факультет МГУ, 2001, 127 с.
- 7.
- А.Н. Павлов, А.Р. Зиганшин, В.С Анищенко. Мультифрактальный анализ
временных рядов. // Известия ВУЗов «ПНД», т.9, №3, 2001 с.39-52.
- 8.
- D. Ruelle and F. Takens. "On the nature of turbulence".
Communications in Mathematical Physics 20 (3), 1971, pp. 167-192.
- 9.
- F. Takens. Detecting strange attractors in turbulence. In D. A. Rand
and L.-S. Young. Dynamical Systems and Turbulence, Lecture Notes in
Mathematics, vol. 898. Springer-Verlag. 1981, pp. 366-381.
- 10.
- D.S.Broomhead, G.P.King. Physica D. 1986. 20. p.217.
- 11.
- M. B. Kennel, R. Brown, and H. D. I. Abarbanel, Determining
embedding dimension for phase-space reconstruction using a geometrical
construction, Phys. Rev. A, 1992, 45, 3403.
- 12.
- S. Arya, D. M. Mount, N. S. Netanyahu, R. Silverman, and A. Y.
Wu. An Optimal Algorithm for Approximate Nearest Neighbour Searching in
Fixed Dimensions. Journal of the ACM, vol. 45, no. 6, pp. 891-923.
- 13.
- A. Gorban, B. Kegl, D. Wunsch, A. Zinovyev (Eds.). Principal
Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58,
Springer, Berlin – Heidelberg – New York, 2007.
- 14.
- Ю.В. Березин, О.Ю. Волков. Поляризационная диагностика и
селективное возбуждение электромагнитных волн в анизотропной
ионосфере. // Информационно-измерительные и управляющие системы. 2004. —
1. — С. 53-57.
- 15.
- R. Hegger, H. Kantz, and T. Schreiber. Practical implementation of
nonlinear time series methods: The TISEAN package, CHAOS 9, 413 (1999)
- 16.
- The TISEAN software package. URL:
http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/index.html
- 17.
- P. Grassberger, I. Procaccia. Characterization of Strange Attractors.
// Physical Review Letters.– 1983.– Vol.50.– P. 346-349.
- 18.
- A. Wolf, J.B. Swift, H.L. Swinney, J.A. Vastano. Determining
Lyapunov exponents from a time series. Physica D, 285-317, 1985.
- 19.
- K.T. Alligood, T.D. Sauer, and J.A. Yorke. Chaos: an Introduction
to Dynamical Systems (Springer 1997) XVIII, 603 p.