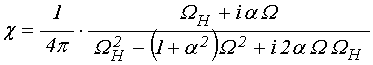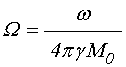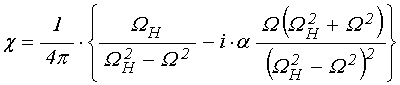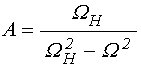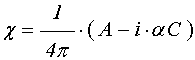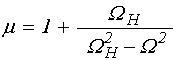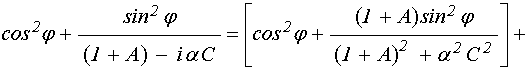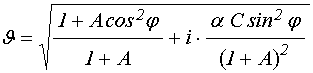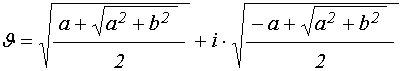УДК 537.874; 537.624
ПОВЕРХНОСТНЫЕ МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНЕ ФЕРРИТА С ДИССИПАЦИЕЙ.
ЧАСТЬ 1. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
Ю. И. Келлер1, П. А. Макаров1, В. Г. Шавров2, В. И. Щеглов2
1 Сыктывкарский государственный университет
2 Институт радиотехники и электроники им. В.А.Котельникова РАН
Статья поступила в редакцию 24 января 2016 г.
Аннотация. На основе последовательного решения уравнения движения для намагниченности проведен учет затухания поверхностных магнитостатических волн (ПМСВ) в касательно намагниченной ферритовой пластине. Выявлен обусловленный диссипацией комплексный характер волнового числа. Рассмотрено приближение малого затухания. Для случая типичных значений параметров материала и частоты возбуждения выполнена оценка его применимости. В таком приближении получены дисперсионные соотношения для действительной и мнимой частей волнового числа.
Ключевые слова: феррит, магнитостатические волны, диссипация.
Abstract. By means of consistent solution of motion equation for magnetization the dissipation for magnetostatic surface waves (MSSW) propagating on in-plane magnetized ferrite plate is considered. The complex character of wave number caused by the dissipation is revealed. The approximation of small value dissipation is investigated. For the case of typical material and excitation frequency parameters appreciation of its employment is found. In this approximation the dispersion relations for real and imaginary parts of wave number are found.
Key words: ferrite, magnetostatic waves, dissipation.
Введение
Поверхностные
магнитостатические волны (ПМСВ) в пленках железоиттриевого граната (ЖИГ) [1],
составляют основу широкого класса устройств аналоговой обработки информации в
диапазоне СВЧ [2-5]. Типичное устройство содержит пленку ЖИГ с расположенными
на ее поверхности излучающим и приемным преобразователями, выполненными в виде
антенн из тонкой проволоки. Диапазон частот таких устройств – ![]() . В плоскости пленки приложено постоянное
магнитное поле напряженностью
. В плоскости пленки приложено постоянное
магнитное поле напряженностью ![]() . Длина антенн
составляет
. Длина антенн
составляет ![]() , расстояние между ними – того же порядка.
Наиболее оптимальная среда для распространения ПМСВ – пленка ЖИГ толщиной
, расстояние между ними – того же порядка.
Наиболее оптимальная среда для распространения ПМСВ – пленка ЖИГ толщиной ![]() , имеющая намагниченность насыщения
, имеющая намагниченность насыщения ![]() . Длина ПМСВ составляет от
. Длина ПМСВ составляет от ![]() до
до ![]() , причем
ослабление волны в процессе распространения за счет диссипации может быть
довольно значительным и составлять по мощности до нескольких десятков децибел.
, причем
ослабление волны в процессе распространения за счет диссипации может быть
довольно значительным и составлять по мощности до нескольких десятков децибел.
В литературе имеется немало работ по распространению ПМСВ в пленках ЖИГ, в том числе в неоднородных полях [6-11] и сложных структурах [12-17], однако вопросам затухания волн уделено внимания крайне недостаточно. В немногих работах на эту тему [18,19] показано, что наличие диссипации приводит к появлению в спектре ПМСВ обратных «диссипативных» волн, по частоте примыкающих к верхней границе спектра обычных прямых ПМСВ типа Дэймона-Эшбаха [1]. Показано, что диссипация приводит к ограничению сверху возможного диапазона волновых чисел как для прямых, так и для обратных волн, причем потери на распространение обратных волн значительно превышают подобные потери для прямых волн.
Однако проведенное в этих работах исследование является недостаточно полным. Рассмотрение базируется на анализе дисперсионного соотношения для ПМСВ, полученного без учета затухания, после чего затухание вводится через посредство комплексной добавки к частоте, что не является вполне последовательным. Полученные выражения не позволяют в достаточной степени выявить причину ограничения спектра ПМСВ не только по волновому числу, но также и по параметру затухания. Роль толщины ферритовой пластины в ее соотношении с длиной волны также остается не выясненной. Рассмотрение проведено в довольно общем виде, затрудняющем сопоставление полученных результатов с реальными экспериментами. Учет роли геометрии возбуждающего ПМСВ преобразователя полностью отсутствует.
Перечисленные недостатки в значительной степени восполнены в работах [20,21]. На основе последовательного решения уравнения движения для намагниченности (уравнения Ландау-Лифшица с диссипативным членом в форме Гильберта [22-25]), проведен учет затухания ПМСВ в касательно намагниченной ферритовой пластине. Выявлено существование диссипативной ветви обратных ПМСВ, лежащей выше по частоте относительно основного спектра прямых ПМСВ, а также ограничение сверху предельных значений волнового числа для обеих ветвей спектра. Рассмотрено ограничение спектра по параметру затухания и роль толщины пластины в соотношении с длиной волны. Проведено сопоставление с опубликованными ранее экспериментальными результатами и даны рекомендации для проведения новых экспериментов.
Несмотря на довольно подробное рассмотрение, перечисленные работы посвящены случаю распространения ПМСВ только в направлении, перпендикулярном полю подмагничивания, что связано с заметной сложностью математического аппарата, учитывающего отклонение направления распространения ПМСВ от перпендикуляра к направлению поля.
В работах [26,27] впервые для случая диссипативной среды рассмотрено распространение ПМСВ в произвольном направлении относительно поля. Построены индикатрисы (изочастотные кривые) прямых ПМСВ и показано, что при учете затухания они идут несколько выше (то есть соответствуют несколько большим углам групповой скорости), чем в отсутствие затухания. Однако дисперсионные свойства как прямых, так и обратных волн не рассмотрены, а приведенные численные оценки не дают исчерпывающего количественного представления о роли затухания в достаточно широком диапазоне изменения диссипации. Возможность обусловленного затуханием ограничения диапазона волновых чисел также не выявлена.
Таким образом, исследование, проведенное в упомянутых работах, является недостаточно полным. Так остается невыясненной роль затухания в формировании законов дисперсии как прямых, так и обратных ПМСВ, распространяющихся в произвольном направлении, а также возможность ограничения в этом случае диапазона возможных волновых чисел. Физическая причина такого ограничения также остается невыясненной, численные оценки условий наблюдения таких явлений в эксперименте отсутствуют.
Настоящая работа является развитием работ [20,21] на случай произвольного направления распространения ПМСВ в плоскости пленки и посвящена в первую очередь получению законов дисперсии, а также выявлению возможности ограничения диапазона волновых чисел ПМСВ в широком диапазоне значений параметра затухания при постоянном его значении, не зависящем от частоты. В первой части работы (настоящая статья) будет рассмотрен лежащий в основе исследования математический аппарат, получены дисперсионные соотношения для действительной и мнимой частей волнового числа. Последующие части предполагается посвятить исследованию законов дисперсии при распространении ПМСВ как в нормальном, так и в произвольном направлениях относительно постоянного поля. Отдельную работу предполагается посвятить зависимости параметра затухания от частоты.
1. Геометрия задачи
Общая геометрия задачи,
совпадающая с принятой в работах [20,21], показана на рис.1. Ферритовая
пластина толщины ![]() намагничена в плоскости полем
намагничена в плоскости полем ![]() . Декартова система координат
. Декартова система координат ![]() выбрана таким образом, что ее начало, точка
выбрана таким образом, что ее начало, точка
![]() , находится на середине толщины пластины,
плоскость
, находится на середине толщины пластины,
плоскость ![]() параллельна плоскости пластины, а ось
параллельна плоскости пластины, а ось ![]() ей перпендикулярна. При этом координаты
плоскостей пластины по оси
ей перпендикулярна. При этом координаты
плоскостей пластины по оси ![]() равны
равны ![]() . Ось
. Ось ![]() ориентирована
вдоль поля
ориентирована
вдоль поля ![]() . Далее рассматриваются поверхностные
магнитостатические волны (ПМСВ), распространяющиеся вдоль верхней поверхности
пластины при
. Далее рассматриваются поверхностные
магнитостатические волны (ПМСВ), распространяющиеся вдоль верхней поверхности
пластины при ![]() . Волновой вектор
. Волновой вектор ![]() лежит
в плоскости
лежит
в плоскости ![]() и составляет угол
и составляет угол ![]() с
осью
с
осью ![]() , вектор групповой скорости
, вектор групповой скорости ![]() лежит в той же плоскости и составляет
угол
лежит в той же плоскости и составляет
угол ![]() с осью
с осью ![]() .
.
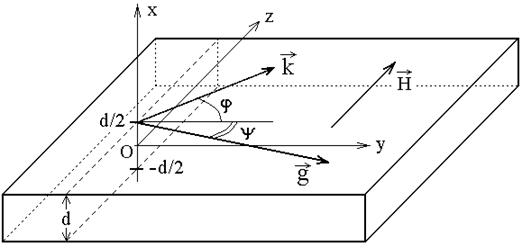
Рис.1. Общая геометрия задачи.
2. Общий вид волновой функции и дисперсионного соотношения
Будем полагать, что среда
является изотропной, а волны возбуждаются пространственно локализованным
источником, колеблющимся с заданной частотой ![]() . Пусть
волновое число является комплексным:
. Пусть
волновое число является комплексным:
где ![]() и
и ![]() – действительные постоянные (
– действительные постоянные (![]() и
и ![]() ).
).
Предположим, что волновая функция имеет вид:
![]() , (2)
, (2)
то есть волна распространяется в
положительном направлении координаты ![]() , отсчитываемой от
источника, причем в процессе распространения амплитуда волны уменьшается по
экспоненте с показателем, пропорциональным мнимой части волнового числа
, отсчитываемой от
источника, причем в процессе распространения амплитуда волны уменьшается по
экспоненте с показателем, пропорциональным мнимой части волнового числа ![]() .
.
Длина волны ![]() определяется соотношением:
определяется соотношением:
![]() , (3)
, (3)
то есть не меняется и задается
действительной частью волнового числа ![]() .
.
Аналогично [20,21], примем определение «дисперсионного соотношения для действительной части волнового числа» в виде:
где ![]() –
функция, определяемая параметрами среды, в том числе параметром затухания.
–
функция, определяемая параметрами среды, в том числе параметром затухания.
Кроме этого потребует
рассмотрения соотношение между частотой ![]() и
мнимой частью волнового числа
и
мнимой частью волнового числа ![]() :
:
которое будем называть «дисперсионным соотношением для мнимой части волнового числа».
3. Магнитная восприимчивость в среде с затуханием
Для описания движения вектора намагниченности в среде с потерями будем пользоваться уравнением Ландау-Лифшица с диссипативным членом в форме Гильберта [22-25]:
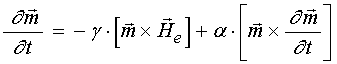 , (6)
, (6)
где ![]() –
нормированный вектор намагниченности,
–
нормированный вектор намагниченности, ![]() –
намагниченность насыщения,
–
намагниченность насыщения, ![]() – гиромагнитная
постоянная (
– гиромагнитная
постоянная (![]() ),
), ![]() –
параметр затухания,
–
параметр затухания, ![]() – эффективное поле, равное:
– эффективное поле, равное:
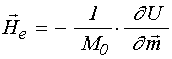 , (7)
, (7)
где ![]() –
плотность магнитной энергии, в рассматриваемой геометрии равная:
–
плотность магнитной энергии, в рассматриваемой геометрии равная:
![]() . (8)
. (8)
Решение уравнения (6) дает компоненты магнитной восприимчивости, имеющие вид [22-24]:
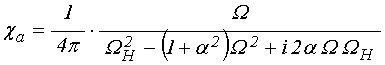 , (10)
, (10)
где введены нормированные частоты:
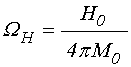 , (12)
, (12)
связывающие частоту ![]() и поле
и поле ![]() с
параметрами материала (намагниченностью
с
параметрами материала (намагниченностью ![]() ).
).
4. Приближение малого затухания
Будем далее считать
потери достаточно малыми, то есть положим ![]() . Освобождаясь
от мнимости в знаменателях выражений (9)-(10) и отбрасывая слагаемые, содержащие
. Освобождаясь
от мнимости в знаменателях выражений (9)-(10) и отбрасывая слагаемые, содержащие
![]() , по сравнению с
, по сравнению с ![]() ,
после чего выделяя в явном виде действительную и мнимую части, приводим
компоненты восприимчивости к виду:
,
после чего выделяя в явном виде действительную и мнимую части, приводим
компоненты восприимчивости к виду:
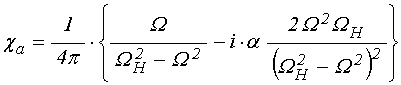 . (14)
. (14)
Запишем эти компоненты в укороченном виде, для чего, подобно [20,21], введем вспомогательные обозначения:
 ; (16)
; (16)
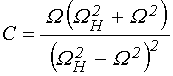 ; (17)
; (17)
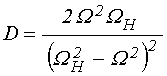 . (18)
. (18)
Правомерность отбрасывания слагаемых, возникающих в (9)-(10) при освобождении от мнимости в знаменателе, требует количественной проверки. Для проведения таковой воспользуемся результатами работ [20,21], где получены предельные значения характерных частот спектра ПМСВ в отсутствие затухания. Так, согласно [20,21] эти значения частот определяются решением уравнения [20, форм.(49)]:
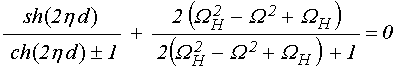 , (19)
, (19)
к которому сводится полученное там дисперсионное
соотношение при ![]() .
.
Решение этого уравнения
относительно частоты ![]() имеет вид:
имеет вид:
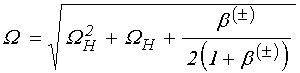 , (20)
, (20)
где ![]() –
вспомогательное обозначение равное:
–
вспомогательное обозначение равное:
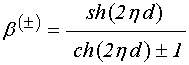 . (21)
. (21)
Из (20)-(21) видно, что
зависимость нормированной частоты ![]() от действительной
части волнового числа
от действительной
части волнового числа ![]() имеет две ветви,
соответствующие знакам «плюс» и «минус».
имеет две ветви,
соответствующие знакам «плюс» и «минус».
Предельные значения
частот обеих ветвей, определяемых этим дисперсионным соотношением при ![]() и
и ![]() имеют
вид:
имеют
вид:
Знак «ПЛЮС»:
![]() , при
этом
, при
этом ![]() :
:
![]() ; (22)
; (22)
![]() , при
этом
, при
этом ![]() :
:
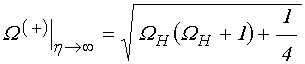 ; (24)
; (24)
Знак «МИНУС»:
![]() , при
этом
, при
этом ![]() :
:
 ; (26)
; (26)
![]() , при
этом
, при
этом ![]() :
:
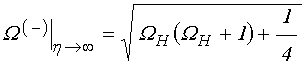 ; (28)
; (28)
![]() . (29)
. (29)
Пользуясь этими
формулами, вычислим значения частот при типичных параметрах эксперимента: ![]() ,
, ![]() , так
что
, так
что ![]() . При этом характерные частоты границ областей
существования прямых и обратных (диссипативных) ПМСВ [20,21] получаются
равными:
. При этом характерные частоты границ областей
существования прямых и обратных (диссипативных) ПМСВ [20,21] получаются
равными:
![]() ,
,
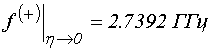 ; (30)
; (30)
![]() ,
,
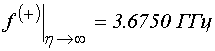 ; (31)
; (31)
![]() ,
,
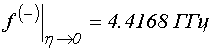 ; (32)
; (32)
![]() ,
,
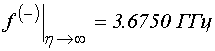 . (33)
. (33)
Можно видеть, что имеются всего три граничных значения нормированных частот:
![]() ; (35)
; (35)
![]() , (36)
, (36)
соответствующие линейным частотам:
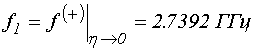 ; (37)
; (37)
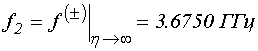 ; (38)
; (38)
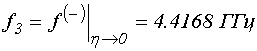 . (39)
. (39)
При этих частотах получаем следующие значения параметров (15)-(18) (индексы параметров соответствуют индексам частот):
![]() ;
; ![]() ;
; ![]() ; (41)
; (41)
![]() ;
; ![]() ;
; ![]() ; (42)
; (42)
![]() ;
; ![]() ;
; ![]() . (43)
. (43)
Из этих оценок видно, что
при принятых типичных условиях эксперимента все параметры (40)-(43) имеют величину
порядка единицы, поэтому слагаемые, получаемые при освобождении (9)-(10) от мнимости
в знаменателе, пропорциональные ![]() , где
, где ![]() , в любом случае будут превышать такие же слагаемые,
пропорциональные
, в любом случае будут превышать такие же слагаемые,
пропорциональные ![]() .
.
Таким образом, отбрасывание
слагаемых, пропорциональных ![]() , в рамках линейного
приближения по
, в рамках линейного
приближения по ![]() можно считать вполне
допустимым.
можно считать вполне
допустимым.
В этом случае в обозначениях (15)-(18) компоненты восприимчивости (13)-(14) принимают вид:
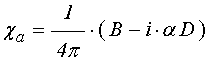 . (45)
. (45)
Таким образом, формулы (44)-(45) представляют собой искомую укороченную запись компонент восприимчивости, которая используется далее.
5. Дисперсионное соотношение в отсутствие диссипации
В описанной геометрии основное дисперсионное соотношение для поверхностных магнитостатических волн в отсутствие затухания имеет вид:
где:
![]() ; (48)
; (48)
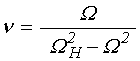 , (50)
, (50)
а ![]() и
и ![]() определяются формулами (11)-(12).
определяются формулами (11)-(12).
Это соотношение в несколько ином виде получено путем решения граничной задачи, впервые описанной в работе [1]. Приведенный здесь вид аналогичен полученному в [1], однако отличается удобством использования в задачах, касающихся распространения ПМСВ в пленке, намагниченной неоднородным полем [6-11].
Для целей настоящей работы приведем это соотношение к более удобному виду, для чего запишем волновое число в полярной системе координат:
![]() ; (52)
; (52)
![]() ; (53)
; (53)
где ![]() определяется
соотношением (47), а также введем вспомогательные обозначения:
определяется
соотношением (47), а также введем вспомогательные обозначения:
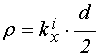 ; (55)
; (55)
![]() . (57)
. (57)
Раскрывая гиперболический котангенс через экспоненты, приводим дисперсионное соотношение (46) к следующему виду:
Замечание. С точки зрения простоты алгебраических выкладок, удобнее выполнить преобразования в обратном порядке: подставить в (58) обозначения (55)-(57) и свести дробь, содержащую экспоненты, к гиперболическому котангенсу, в результате чего с учетом (51)-(54) будет получено выражение (46).
6. Упрощенное преобразование
параметра ![]()
Приведем вариант
упрощенной записи параметра ![]() в приближении малого затухания
при учете комплексного характера волнового числа.
в приближении малого затухания
при учете комплексного характера волнового числа.
Согласно (47), при
произвольном угле ![]() параметр
параметр ![]() в знаменателе подкоренной дроби содержит
величину
в знаменателе подкоренной дроби содержит
величину ![]() , в отсутствие затухания определяемую соотношением
(49). Однако из сравнения (49) с (13) можно видеть, что при
, в отсутствие затухания определяемую соотношением
(49). Однако из сравнения (49) с (13) можно видеть, что при ![]() параметр
параметр ![]() принимает
вид:
принимает
вид:
![]() . (59)
. (59)
При учете затухания надо
использовать полное выражение для ![]() , в укороченном виде
определяемое соотношением (44). При этом получаем параметр
, в укороченном виде
определяемое соотношением (44). При этом получаем параметр ![]() в виде:
в виде:
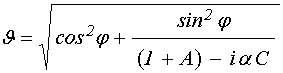 . (60)
. (60)
В подкоренном выражении освободимся от мнимости в знаменателе дроби и выделим по отдельности действительную и мнимую части:
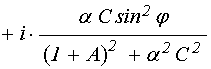 . (61)
. (61)
Из численных оценок
величин ![]() и
и ![]() (40)-(43)
видно, что на частотах выше
(40)-(43)
видно, что на частотах выше ![]() хотя бы на
хотя бы на ![]() при
при ![]() второе
слагаемое в знаменателе этих дробей всегда намного меньше первого, так что им
по сравнению с первым можно пренебречь. При этом получаем:
второе
слагаемое в знаменателе этих дробей всегда намного меньше первого, так что им
по сравнению с первым можно пренебречь. При этом получаем:
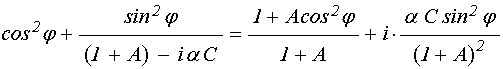 . (62)
. (62)
Подставляя это выражение в (60), получаем:
Для разделения действительной и мнимой частей этого выражения воспользуемся формулой квадратного корня из комплексного числа:
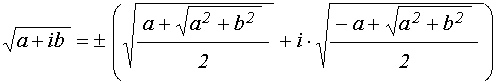 . (64)
. (64)
Параметр ![]() содержится в дисперсионном соотношении (46)
только в виде произведения
содержится в дисперсионном соотношении (46)
только в виде произведения ![]() . Можно видеть, что
при изменении знака
. Можно видеть, что
при изменении знака ![]() это произведение не меняется,
то есть знак перед скобками в правой части (64) безразличен. Поэтому для простоты
можно взять «плюс», в результате чего получаем:
это произведение не меняется,
то есть знак перед скобками в правой части (64) безразличен. Поэтому для простоты
можно взять «плюс», в результате чего получаем:
где:
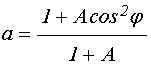 ; (66)
; (66)
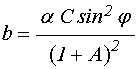 . (67)
. (67)
Найдем подкоренное выражение внутреннего корня:
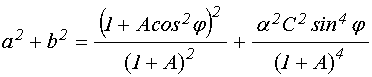 . (68)
. (68)
При учете оценок (40)-(43)
можно видеть, что в случае ![]() при удалении от
при удалении от ![]() хотя бы на
хотя бы на ![]() второе
слагаемое значительно меньше первого, так что им можно пренебречь. При этом
получаем внутренний корень выражения (65) в виде:
второе
слагаемое значительно меньше первого, так что им можно пренебречь. При этом
получаем внутренний корень выражения (65) в виде:
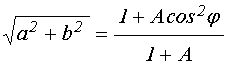 . (69)
. (69)
Здесь при извлечении
корня оставлен знак «плюс», так как предельное значение ![]() (63)
при
(63)
при ![]() в случае плюса дает
в случае плюса дает ![]() , как это получается при параллельно-перпендикулярной
геометрии, принятой в работах [20,21], тогда как в случае минуса –
, как это получается при параллельно-перпендикулярной
геометрии, принятой в работах [20,21], тогда как в случае минуса – ![]() , что случаю принятой там геометрии противоречит.
, что случаю принятой там геометрии противоречит.
Подставляя (69) в (65) и выполняя сложение, можно видеть, что второе слагаемое в формуле (65) обращается в нуль, в результате чего получаем:
Здесь, согласно оценкам (40)-(43),
величина ![]() , определяемая формулой (15), отрицательна
и меньше единицы, а
, определяемая формулой (15), отрицательна
и меньше единицы, а ![]() также всегда меньше или равен
единице, так что как числитель, так и знаменатель подкоренной дроби всегда
положительны, то есть рассчитываемое по этой формуле значение
также всегда меньше или равен
единице, так что как числитель, так и знаменатель подкоренной дроби всегда
положительны, то есть рассчитываемое по этой формуле значение ![]() всегда действительное.
всегда действительное.
Подставляя значение ![]() в соответствии с (15), получаем
в соответствии с (15), получаем
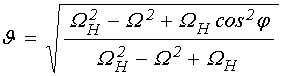 . (71)
. (71)
Записанное в таком виде
значение ![]() в интервале частот, определяемом (34)-(36),
является действительным и при
в интервале частот, определяемом (34)-(36),
является действительным и при ![]() обращается в единицу,
что совпадает с [20,21].
обращается в единицу,
что совпадает с [20,21].
Напомним, что в
соответствии с (61), такое представление ![]() достаточно
справедливо лишь на частотах, которые выше
достаточно
справедливо лишь на частотах, которые выше ![]() хотя
бы на
хотя
бы на ![]() . Однако наибольший интерес представляет
рассмотрение дисперсии ПМСВ вблизи частоты
. Однако наибольший интерес представляет
рассмотрение дисперсии ПМСВ вблизи частоты ![]() ,
большей
,
большей ![]() в полтора раза, где ожидается ограничение
предельного значения волнового числа, поэтому представление (70)-(71) в этом
случае можно считать вполне правомерным.
в полтора раза, где ожидается ограничение
предельного значения волнового числа, поэтому представление (70)-(71) в этом
случае можно считать вполне правомерным.
7. Общий вид дисперсионного соотношения для действительной части волнового числа
Будем исходить из дисперсионного соотношения в виде (58):
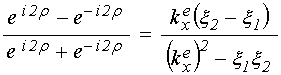 , (72)
, (72)
где в соответствии с (54)-(55):
![]() ; (73)
; (73)
![]() , (74)
, (74)
а параметры ![]() и
и
![]() , будучи записанными через компоненты
восприимчивости
, будучи записанными через компоненты
восприимчивости ![]() и
и ![]() ,
согласно (56)-(57), имеют вид.
,
согласно (56)-(57), имеют вид.
![]() ; (75)
; (75)
![]() .
(76)
.
(76)
Входящие в (72)
промежуточные соотношения, содержащие ![]() и
и ![]() , имеют вид:
, имеют вид:
![]() ; (77)
; (77)
![]() . (78)
. (78)
В таком виде дисперсионное
соотношение получено без какого-либо предположения о действительном или
комплексном характере входящих в него величин, то есть имеет наиболее общий
вид. Для учета затухания надо волновое число ![]() ,
параметр
,
параметр ![]() и компоненты восприимчивости
и компоненты восприимчивости ![]() и
и ![]() записать
в комплексном виде. С целью упрощения дальнейших вычислений, введем вспомогательные
обозначения левой и правой частей дисперсионного соотношения (72):
записать
в комплексном виде. С целью упрощения дальнейших вычислений, введем вспомогательные
обозначения левой и правой частей дисперсионного соотношения (72):
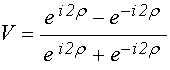 ; (79)
; (79)
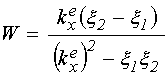 . (80)
. (80)
В этих обозначениях дисперсионное соотношение (72) имеет вид:
Подставляя (73)-(78) в (79)-(80), получаем:
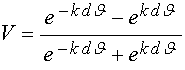 ; (82)
; (82)
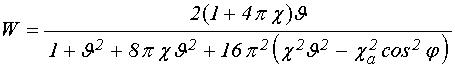 . (83)
. (83)
Выполним преобразование этих частей по отдельности.
8. Преобразование левой части дисперсионного соотношения
Преобразуем сначала левую
часть дисперсионного соотношения (81), имеющую вид (82). В этом выражении
волновое число ![]() является комплексным:
является комплексным:
![]() . (84)
. (84)
Подставляя в показатели экспонент комплексное волновое число в виде (84) и пользуясь формулой Эйлера, получаем:
![]() ; (85)
; (85)
![]() . (86)
. (86)
Подставляя (84)-(86) в (82) и приводя подобные члены, получаем:
 . (87)
. (87)
Освобождаемся от мнимости в знаменателе:
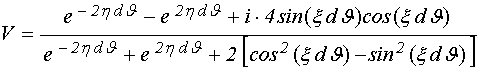 . (88)
. (88)
Пользуясь формулами двойного угла и выделяя действительную и мнимую части в явном виде, получаем:
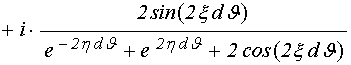 . (89)
. (89)
9. Преобразование правой части дисперсионного соотношения
Преобразуем теперь правую часть дисперсионного соотношения (81), имеющую вид (83):
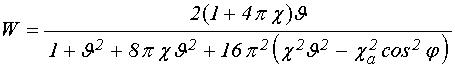 . (90)
. (90)
В это выражение входят компоненты
тензора восприимчивости, с точностью до первой степени параметра ![]() , имеющие вид (44)-(45), с учетом обозначений
(15)-(18), а параметр
, имеющие вид (44)-(45), с учетом обозначений
(15)-(18), а параметр ![]() в том же приближении является
действительным и определяется выражением (70).
в том же приближении является
действительным и определяется выражением (70).
Подставляя (44)-(45), выполняя
действия и отбрасывая слагаемые, содержащие ![]() ,
получаем:
,
получаем:
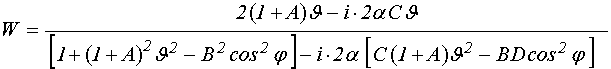 .
(91)
.
(91)
Введем еще одну группу вспомогательных обозначений:
![]() ; (93)
; (93)
![]() ; (94)
; (94)
![]() . (95)
. (95)
Можно видеть, что,
согласно действительности ![]() , эти выражения также
являются действительными.
, эти выражения также
являются действительными.
В обозначениях (92)-(95) правая часть (91) принимает вид:
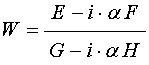 . (96)
. (96)
Освобождаясь от мнимости в знаменателе, получаем:
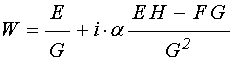 . (97)
. (97)
Для упрощения дальнейших вычислений введем еще некоторые дополнительные обозначения:
 . (99)
. (99)
В этих обозначениях (96) принимает вид:
![]() . (100)
. (100)
Итак здесь ![]() и
и ![]() определяются
выражениями (98) и (99), входящие в них величины
определяются
выражениями (98) и (99), входящие в них величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() – выражениями (92)-(95), которые в свою
очередь определяются через частоты посредством выражений (15)-(18) и (70)-(71).
Таким образом, выражения
– выражениями (92)-(95), которые в свою
очередь определяются через частоты посредством выражений (15)-(18) и (70)-(71).
Таким образом, выражения ![]() и
и ![]() полностью определяются частотами
полностью определяются частотами ![]() и
и ![]() в
сочетании с заданным значением угла
в
сочетании с заданным значением угла ![]() .
.
10. Полное дисперсионное соотношение
Теперь, когда левая и правая части дисперсионного соотношения получены, запишем его полностью. Чтобы не создавать излишней громоздкости записи, выражения (98) и (99) оставим в сокращенном виде. Итак, подставляя (89) и (100) в (81), получаем:
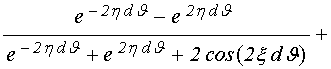
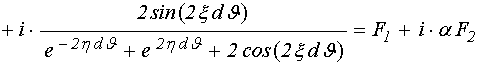 . (101)
. (101)
Группируя действительную и мнимую части по отдельности, получаем:
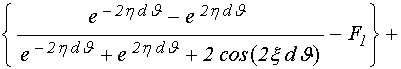
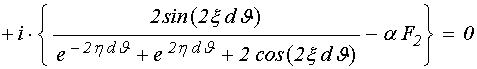 . (102)
. (102)
Приравнивая действительную и мнимую части этого выражения к нулю, получаем систему двух уравнений:
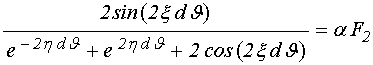 . (104)
. (104)
Правые части этих
уравнений содержат только частоты ![]() и
и ![]() . В левые части входят только
действительная и мнимая компоненты волнового числа
. В левые части входят только
действительная и мнимая компоненты волнового числа ![]() и
и ![]() .
.
Поскольку частота ![]() задана постоянным полем (как параметр
среды), то есть неизменна, полученные уравнения можно рассматривать как
систему, связывающую три переменных
задана постоянным полем (как параметр
среды), то есть неизменна, полученные уравнения можно рассматривать как
систему, связывающую три переменных ![]() ,
, ![]() и
и ![]() .
Поскольку переменных три, а уравнений всего два, то одна из переменных может
быть задана произвольно. В соответствии с условием задачи (волна постоянной
частоты спадает в пространстве), частоту
.
Поскольку переменных три, а уравнений всего два, то одна из переменных может
быть задана произвольно. В соответствии с условием задачи (волна постоянной
частоты спадает в пространстве), частоту ![]() будем
считать заданной. Тогда (103)-(104) обращается в систему двух уравнений
относительно
будем
считать заданной. Тогда (103)-(104) обращается в систему двух уравнений
относительно ![]() и
и ![]() .
.
Положим, что основу
будущего дисперсионного соотношения, содержащего только действительную часть
волнового числа ![]() и частоту
и частоту ![]() , должно составить первое уравнение (103),
которое однако содержит еще и
, должно составить первое уравнение (103),
которое однако содержит еще и ![]() в виде
в виде ![]() . Чтобы исключить из первого уравнения
мнимую компоненту волнового числа
. Чтобы исключить из первого уравнения
мнимую компоненту волнового числа ![]() , надо выразить ее из
второго уравнения (104) через действительную компоненту
, надо выразить ее из
второго уравнения (104) через действительную компоненту ![]() и
функцию
и
функцию ![]() . Это вполне можно сделать, так как
. Это вполне можно сделать, так как ![]() зависит только от частоты и компонент
волнового числа не содержит. Таким образом, из второго уравнения (104) надо
найти
зависит только от частоты и компонент
волнового числа не содержит. Таким образом, из второго уравнения (104) надо
найти ![]() , который затем и будет подставлен в
первое уравнение.
, который затем и будет подставлен в
первое уравнение.
Введем еще некоторые вспомогательные обозначения:
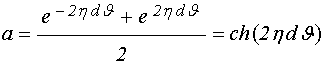 . (105)
. (105)
![]() ; (106)
; (106)
![]() . (107)
. (107)
С этими обозначениями уравнение (104) принимает вид:
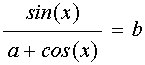 . (108)
. (108)
Выражая синус через
косинус и возводя в квадрат, получаем уравнение для ![]() :
:
Это уравнение – квадратное. Его решение имеет вид:
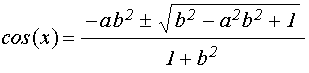 . (110)
. (110)
Подставляя обозначения (105)-(107) и учитывая соотношение:
![]() , (111)
, (111)
где ![]() –
произвольное число, получаем:
–
произвольное число, получаем:
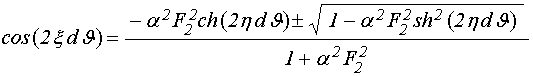 . (112)
. (112)
Подставляя это выражение в (103), получаем искомое дисперсионное соотношение для действительной части волнового числа задачи Дэймона-Эшбаха в среде с затуханием в виде:
 (113)
(113)
Преобразуя первое слагаемое (113) с помощью определений гиперболических функций, это соотношение можно записать в несколько более компактном виде:
Освобождаясь от дроби, получаем:
Это дисперсионное
соотношение зависит только от ![]() и
и ![]() через функции
через функции ![]() и
и ![]() , которые определяются выражениями (98)-(99),
куда
, которые определяются выражениями (98)-(99),
куда ![]() входит как параметр.
входит как параметр.
Как будет показано в следующем разделе, знак «плюс» здесь соответствует прямым ПМСВ, переходящим в отсутствие диссипации в классическое соотношение Дэймона-Эшбаха [1], а знак «минус» соответствует обратным диссипативным ПМСВ, классического аналога не имеющим.
В явном виде относительно
![]() или
или ![]() это
уравнение, по-видимому, не разрешается. Чтобы построить зависимость
это
уравнение, по-видимому, не разрешается. Чтобы построить зависимость ![]() от
от ![]() в
численном виде, его можно разрешить, задавая с определенным шагом волновое
число
в
численном виде, его можно разрешить, задавая с определенным шагом волновое
число ![]() и находя на каждом шаге частоту
и находя на каждом шаге частоту ![]() с помощью алгоритма поиска нуля.
с помощью алгоритма поиска нуля.
Замечание. Из структуры соотношений (113)-(115)
можно видеть, что они содержат параметр ![]() во
второй степени. Следуя логике линейного приближения, слагаемые, содержащие
во
второй степени. Следуя логике линейного приближения, слагаемые, содержащие ![]() , следовало бы опустить. Однако очевидно,
что в этом случае затухание из задачи будет полностью исключено, так как
какие-либо члены, содержащие
, следовало бы опустить. Однако очевидно,
что в этом случае затухание из задачи будет полностью исключено, так как
какие-либо члены, содержащие ![]() в первой степени, в
выражениях (113)-(115) отсутствуют. Поэтому с целью учета затухания слагаемые с
в первой степени, в
выражениях (113)-(115) отсутствуют. Поэтому с целью учета затухания слагаемые с
![]() должны быть сохранены. Квадрат же
получился из-за того, что в основе нахождения дисперсионного соотношения лежит
система уравнений (103)-(104), в которую
должны быть сохранены. Квадрат же
получился из-за того, что в основе нахождения дисперсионного соотношения лежит
система уравнений (103)-(104), в которую ![]() входит
в первой степени в составе сочетания
входит
в первой степени в составе сочетания ![]() . Далее эта система сводится
к квадратному уравнению (109), решение которого и приводит к возведению
упомянутого сочетания в квадрат без первой степени параметра
. Далее эта система сводится
к квадратному уравнению (109), решение которого и приводит к возведению
упомянутого сочетания в квадрат без первой степени параметра ![]() .
.
11. Предельный переход к соотношению Дэймона-Эшбаха
Рассмотрим теперь, как полученное решение соотносится с классическим дисперсионным соотношением задачи Дэймона-Эшбаха [1].
В отсутствие затухания,
то есть при ![]() из (115) получаем:
из (115) получаем:
Рассмотрим сначала знак «плюс». В этом случае с помощью формул для гиперболических функций двойного угла это соотношение можно привести к виду:
![]() . (117)
. (117)
Здесь ![]() определяется формулой (98) с учетом (92),
(94):
определяется формулой (98) с учетом (92),
(94):
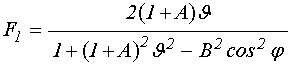 , (118)
, (118)
где ![]() и
и ![]() определяются формулами (15), (16).
определяются формулами (15), (16).
Полученное при решении задачи Дэймона-Эшбаха [1] дисперсионное соотношение без учета затухания для изотропной ферритовой пластины со свободными поверхностями, намагниченной в плоскости, с точностью до обозначений, имеет вид (46):
![]() . (119)
. (119)
или:
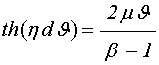 , (120)
, (120)
где входящие в это выражение параметры определяются формулами (47)-(50).
Подстановка (47)-(50) в (120)
показывает тождество выражений (117) и (120), что доказывает выполнение
предельного перехода полученного решения (115) со знаком «плюс» при ![]() к решению классической задачи Дэймона-Эшбаха,
полученному без учета затухания.
к решению классической задачи Дэймона-Эшбаха,
полученному без учета затухания.
Рассмотрим теперь в выражении (116) знак «минус». Выполняя аналогичные преобразования получаем:
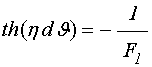 . (121)
. (121)
Можно видеть, что это
выражение при ![]() к соотношению Дэймона-Эшбаха (120)
не сводится, то есть предельный переход не имеет места. С другой стороны, согласно
работам [20,21], посвященным случаю
к соотношению Дэймона-Эшбаха (120)
не сводится, то есть предельный переход не имеет места. С другой стороны, согласно
работам [20,21], посвященным случаю ![]() , решение с минусом
соответствует дисперсионному соотношению для обратных диссипативных волн.
, решение с минусом
соответствует дисперсионному соотношению для обратных диссипативных волн.
Можно полагать, что в
рассматриваемом здесь случае произвольного значения ![]() (в
пределах угла отсечки), волны, описываемые соотношением (121), также являются
диссипативными. Как показано в тех же работах, диссипативные волны имеют место
только при наличии затухания, тогда как в классической задаче Дэймона-Эшбаха
затухание отсутствует, поэтому диссипативная ветвь не реализуется, что и
проявляется в отсутствии соответствующего решения.
(в
пределах угла отсечки), волны, описываемые соотношением (121), также являются
диссипативными. Как показано в тех же работах, диссипативные волны имеют место
только при наличии затухания, тогда как в классической задаче Дэймона-Эшбаха
затухание отсутствует, поэтому диссипативная ветвь не реализуется, что и
проявляется в отсутствии соответствующего решения.
12. Дисперсионное соотношение для мнимой части волнового числа
В проводимом рассмотрении
волновое число ![]() предполагается комплексным в виде
(1). Полученное в разделе №10 дисперсионное соотношение (115) связывает частоту
предполагается комплексным в виде
(1). Полученное в разделе №10 дисперсионное соотношение (115) связывает частоту
![]() с действительной частью волнового числа
с действительной частью волнового числа ![]() , которая определяет только длину распространяющейся
волны, но не содержит информации о ее амплитуде. В среде с диссипацией
амплитуда волны по мере распространения уменьшается, что определяется мнимой
частью волнового числа
, которая определяет только длину распространяющейся
волны, но не содержит информации о ее амплитуде. В среде с диссипацией
амплитуда волны по мере распространения уменьшается, что определяется мнимой
частью волнового числа ![]() . Получим теперь связь между
частотой
. Получим теперь связь между
частотой ![]() и мнимой частью волнового числа
и мнимой частью волнового числа ![]() , которую будем называть «дисперсионным
соотношением для мнимой чисти волнового числа».
, которую будем называть «дисперсионным
соотношением для мнимой чисти волнового числа».
Получение дисперсионного
соотношения в общем случае базируется на решении системы уравнений (103)-(104).
Правые части этих уравнений содержат только частоты ![]() и
и ![]() . В левые части входят только
действительная и мнимая компоненты волнового числа
. В левые части входят только
действительная и мнимая компоненты волнового числа ![]() и
и ![]() .
.
При заданной частоте ![]() эта система связывает две неизвестных –
действительную и мнимую компоненты волнового числа
эта система связывает две неизвестных –
действительную и мнимую компоненты волнового числа ![]() и
и ![]() . В разделе №10 из этой системы была исключена
неизвестная
. В разделе №10 из этой системы была исключена
неизвестная ![]() , что позволило свести ее к одному
уравнению с одной неизвестной
, что позволило свести ее к одному
уравнению с одной неизвестной ![]() (115), представляющему
собой дисперсионное соотношение для действительной части волнового числа, общий
вид которого представлен формулой (4). Исключение из системы (103)-(104) другой
неизвестной
(115), представляющему
собой дисперсионное соотношение для действительной части волнового числа, общий
вид которого представлен формулой (4). Исключение из системы (103)-(104) другой
неизвестной ![]() позволяет получить одно уравнение относительно
другой неизвестной
позволяет получить одно уравнение относительно
другой неизвестной ![]() , что и даст дисперсионное
соотношение для мнимой части волнового числа, которое будет иметь вид (5).
, что и даст дисперсионное
соотношение для мнимой части волнового числа, которое будет иметь вид (5).
Выполним теперь такое исключение, для чего с целью упрощения выкладок сначала введем вспомогательные обозначения:
![]() ; (123)
; (123)
![]() , (124)
, (124)
где ![]() определяется
соотношением:
определяется
соотношением:
![]() . (125)
. (125)
В этих обозначениях система (103)-(104) принимает вид:
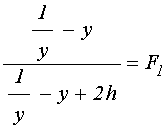 ; (126)
; (126)
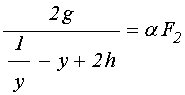 . (127)
. (127)
Освобождаясь в этих уравнениях от дробей, приведем ту же систему к виду:
![]() ; (128)
; (128)
![]() . (129)
. (129)
Совокупность выражений (128)-(129)
представляет собой систему двух квадратных уравнений относительно ![]() , содержащую кроме частоты
, содержащую кроме частоты ![]() также
также ![]() и
и ![]() . Для того, чтобы получить соотношение
между
. Для того, чтобы получить соотношение
между ![]() и
и ![]() типа (5),
из полной системы надо исключить
типа (5),
из полной системы надо исключить ![]() . Из (122)-(124) можно
видеть, что в уравнения (128)-(129) величина
. Из (122)-(124) можно
видеть, что в уравнения (128)-(129) величина ![]() входит
только через посредство
входит
только через посредство ![]() , поэтому из системы (128)-(129)
достаточно исключить
, поэтому из системы (128)-(129)
достаточно исключить ![]() .
.
В отсутствие затухания,
то есть при ![]() второе уравнение через посредство (123) и
(125) дает:
второе уравнение через посредство (123) и
(125) дает: ![]() , то есть волновое число становится чисто
действительным. При этом в соответствии с (123) получаем
, то есть волновое число становится чисто
действительным. При этом в соответствии с (123) получаем ![]() , то есть
, то есть ![]() , в
результате чего первое уравнение при выражении экспонент через гиперболические
функции переходит в классическое дисперсионное соотношение Дэймона-Эшбаха вида
(116) со знаком «плюс» (раздел №11):
, в
результате чего первое уравнение при выражении экспонент через гиперболические
функции переходит в классическое дисперсионное соотношение Дэймона-Эшбаха вида
(116) со знаком «плюс» (раздел №11):
![]() . (130)
. (130)
Таким образом, поскольку
закон дисперсии для действительной части волнового числа получается из первого
уравнения системы (128)-(129), тогда как второе к волновому числу дает только
мнимую добавку, примем за основу именно первое уравнение, а вторым
воспользуемся только для того, чтобы исключить ![]() из
первого. Для такого исключения найдем из второго уравнения
из
первого. Для такого исключения найдем из второго уравнения ![]() и полученное выражение подставим в
первое.
и полученное выражение подставим в
первое.
Разрешая (129)
относительно ![]() по формуле решения квадратного уравнения,
получаем:
по формуле решения квадратного уравнения,
получаем:
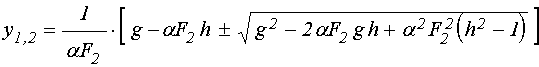 . (131)
. (131)
Заметим, что здесь
параметр затухания ![]() входит в знаменателе первой
дроби, так что получаемые далее выражения будут сохранять корректность только
при
входит в знаменателе первой
дроби, так что получаемые далее выражения будут сохранять корректность только
при ![]() . Однако общности проводимого рассмотрения
это не ограничивает, так как рассмотрение затухания предполагает именно отличие
параметра
. Однако общности проводимого рассмотрения
это не ограничивает, так как рассмотрение затухания предполагает именно отличие
параметра ![]() от нуля.
от нуля.
Отметим далее, что под
корнем присутствуют слагаемые, содержащие как ![]() , так и
, так и
![]() . Полагая
. Полагая ![]() можно
слагаемым с
можно
слагаемым с ![]() пренебречь, в результате чего получаем:
пренебречь, в результате чего получаем:
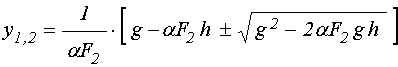 . (132)
. (132)
Возводя это выражение в
квадрат и пренебрегая слагаемыми второго порядка по ![]() в
сравнении с первым, получаем:
в
сравнении с первым, получаем:
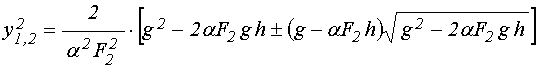 . (133)
. (133)
Подставляя (132)-(133) в
(128) и приводя подобные члены, получаем уравнение, не содержащее ![]() :
:
![]()
![]() . (134)
. (134)
Предельный переход при ![]() приводит к выражению:
приводит к выражению:
![]() , (135)
, (135)
из которого следует, что безусловное
равенство нулю мнимой части комплексного волнового числа ![]() , следующие из условия
, следующие из условия ![]() , имеет место только при знаке «плюс».
Таким образом соотношение (134) принимает вид:
, имеет место только при знаке «плюс».
Таким образом соотношение (134) принимает вид:
![]()
![]() . (136)
. (136)
Это – искомое
дисперсионное соотношение для мнимой части волнового числа, записанное через
вспомогательные обозначения (123)-(125). Оно содержит мнимую часть волнового
числа ![]() , входящую в
, входящую в ![]() и
и ![]() в соответствии с (123)-(124), а также
частоту
в соответствии с (123)-(124), а также
частоту ![]() , входящую в
, входящую в ![]() и
и ![]() в соответствии с приведенными в разделе №9
формулами (98) и (99) с учетом (92)-(95) и (70)-(71).
в соответствии с приведенными в разделе №9
формулами (98) и (99) с учетом (92)-(95) и (70)-(71).
Подставляя (123)-(124) в
(136) и учитывая (125), получаем дисперсионное соотношение, записанное в явном
виде относительно ![]() :
:
![]()
![]() , (137)
, (137)
где ![]() и
и ![]() определяются выражениями (98) и (99) с
учетом (92)-(95) и (70)-(71), зависящими от
определяются выражениями (98) и (99) с
учетом (92)-(95) и (70)-(71), зависящими от ![]() и
содержащими
и
содержащими ![]() в качестве параметра.
в качестве параметра.
В явном виде относительно
![]() или
или ![]() это
уравнение не разрешается. Чтобы построить зависимость
это
уравнение не разрешается. Чтобы построить зависимость ![]() от
от
![]() в численном виде, его можно разрешить, задавая
с определенным шагом мнимую часть волнового числа
в численном виде, его можно разрешить, задавая
с определенным шагом мнимую часть волнового числа ![]() и находя
на каждом шаге частоту
и находя
на каждом шаге частоту ![]() с помощью алгоритма поиска нуля.
с помощью алгоритма поиска нуля.
Таким образом в разделах №10 и №12 получены дисперсионные соотношения с учетом диссипации для действительной (114) и мнимой (137) частей волнового числа. Дальнейший анализ этих соотношений в случае параметров, близких к реальному эксперименту будет проведен в следующих частях настоящей работы.
Заключение
В геометрии плоскопараллельной намагниченной в плоскости ферритовой пластины получено дисперсионное соотношение для поверхностных магнитостатических волн, записанное через экспоненциальные функции от комплексного волнового числа и действительной частоты.
Подстановка в полученное соотношение комплексной магнитной восприимчивости, найденной из решения уравнения движения для намагниченности Ландау-Лифшица с диссипативным членом в форме Гильберта, позволила в явном виде выделить компоненты, определяющие действительную и мнимую части комплексного волнового числа.
Приведены основные алгоритмы численного расчета обеих компонент волнового числа, групповой скорости и времени установления стационарной амплитуды колебаний намагниченности.
На основе анализа общего характера волновой функции введены определения дисперсионного соотношения для действительной и мнимой частей волнового числа. Получено уравнение, определяющее частотные границы областей существования прямых и обратных поверхностных магнитостатических волн, найдены характерные значения частот.
Рассмотрено приближение малого затухания. Для случая типичных значений параметров материала и частоты возбуждения выполнена оценка его применимости. В таком приближении получены компоненты динамической магнитной восприимчивости в среде с диссипацией.
Для общего случая распространения волны в плоскости пластины в произвольном направлении относительно постоянного поля получено общее дисперсионное соотношение, в полярной системе координат выражаемое через экспоненты, показатели которых зависят от комплексного волнового числа. На основе анализа такого соотношения выявлены две его ветви, разделенные по частоте граничным значением, соответствующим стремлению действительной части волнового числа к бесконечности.
Показано, что волны, лежащие по частоте ниже критического значения являются прямыми и в пределе отсутствия затухания переходят в классические волны типа Дэймона-Эшбаха, тогда как волны, лежащие по частоте выше предельного значения являются обратными, классического аналога не имеют и в отсутствие затухания также отсутствуют.
Благодарность
Авторы признательны сотрудникам ИРЭ РАН (Фрязинской части): д.ф.-м.н. В.И.Зубкову, д.ф.-м.н. Э.Г.Локку и д.ф.-м.н. А.В.Вашковскому за консультации на начальном этапе работы, а также д.ф.-м.н. С.В. Герусу и к.ф.-м.н. А.Ю.Анненкову за ознакомление с материалами работ [26,27]. Отдельная благодарность к.ф.-м.н. В.С.Власову (СыктГУ) за внимание к работе и многочисленные стимулирующие замечания.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Damon R.W., Eshbach J.R. // J. Phys. Chem. Solids. 1961. V.19 №3/4. P.308.
2. Адам Дж.Д. // ТИИЭР. 1988. Т.76. №2. С.73.
3. Исхак В.С. // ТИИЭР. 1988. Т.76. №2. С.86.
4. Шлеман Э.Ф. // ТИИЭР. 1988. Т.76. №2. С.105.
5. Adam J., Davis L., Dionne G., Schloemann E., Stitzer S. // IEEE Trans. on MTT. 2002. V.50. №3. P.721.
6. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.1.
7. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.5.
8. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ЖТФ. 1990. Т.60. №7. С.138.
9. Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1990. Т.35. №8. С.1617.
10. Vashkovsky A.V., Lock E.H., Shcheglov V.I., Zubkov V.I. // IEEE Trans. on Magn. 1990. V. Mag-26. №5. P.1480.
11. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1991. Т.36. №1. С.18.
12. Зубков В.И., Щеглов В.И. // РЭ. 2000. Т.45. №4. С.471.
13. Зубков В.И., Щеглов В.И. // РЭ. 2001. Т.46. №4. С.433.
14. Зубков В.И., Щеглов В.И. // РЭ. 2006. Т.51. №3. С.328.
15. Зубков В.И., Щеглов В.И. // РЭ. 2007. Т.52. №6. С.701.
16. Зубков В.И., Щеглов В.И. // РЭ. 2009. Т.54. №9. С.1064.
17. Зубков В.И., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.565.
18. Вызулин С.А., Розенсон А.Э., Шех С.А. // РЭ. 1991. Т.36. №1. С.164-168.
19. Вызулин С.А. Обобщенные плоские волны в задачах электродинамики магнитогиротропных сред. Диссертация. на соискание ученой степени д.ф.-м.н. Краснодар. 2000.
20. Макаров П.А., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2014. №7. С.1-31. http://jre.cplire.ru/jre/jul14/8/text.html, http://jre.cplire.ru/jre/jul14/8/text.pdf.
21. Макаров П.А., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.221-236.
22. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос.Изд.физ.-мат.лит. 1960.
23. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.
24. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.
25. Gilbert T.L. // IEEE Trans. on Magn. 2004. V.40. №6. P.3443.
26. Annenkov А.Yu., Gerus S.V. // Book of Abstracts of Moscow International Symposium on Magnetism (MISM). 2014. Published by “Изд-во Физ.фак. МГУ". Moscow. P.863.
27. Анненков А.Ю., Герус С.В. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.99-102.