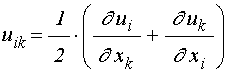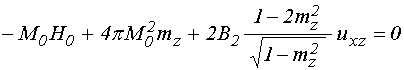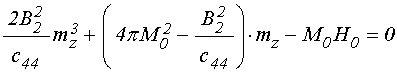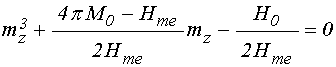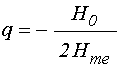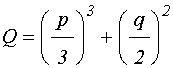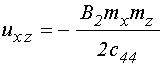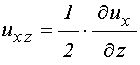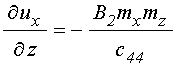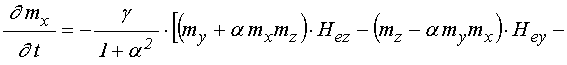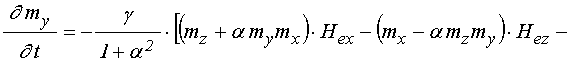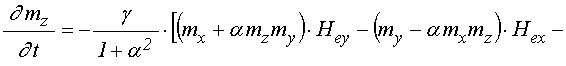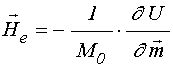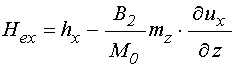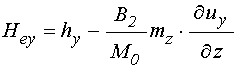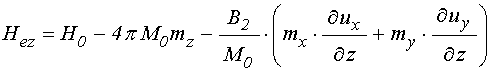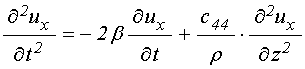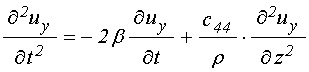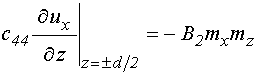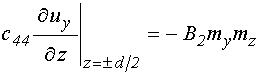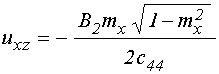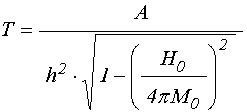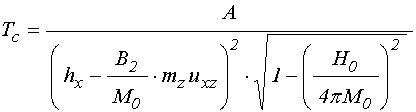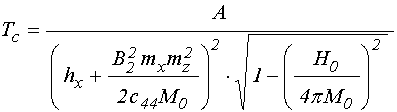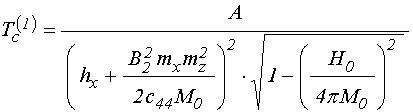УДК 537.874; 537.624
ПРЕЦЕССИЯ НАМАГНИЧЕННОСТИ ВТОРОГО ПОРЯДКА В МАГНИТОУПРУГОЙ СРЕДЕ
В. С. Власов 1, М. С. Кирушев 1, В. Г. Шавров 2, В. И. Щеглов 2
1 Сыктывкарский государственный университет
2 Институт радиотехники и электроники им. В.А.Котельникова РАН
Статья получена 12 апреля 2015 г.
Аннотация. Рассмотрена вынужденная нелинейная прецессия намагниченности второго порядка в нормально намагниченной пластине, обладающей магнитоупругими свойствами. Исследован ориентационный переход вектора намагниченности, состоящий в изменении положения равновесия вектора при изменении константы магнитоупругости. Получена система уравнений для равновесного положения вектора намагниченности относительно компонент намагниченности и упругого смещения, решенная методом Кардано. Получены параметрические портреты для намагниченности и упругого смещения, выявлена роль магнитоупругости в их геометрических свойствах на основе модели потенциала. Для интерпретации зависимости периода прецессии от величины константы магнитоупругого взаимодействия предложены две модели – эффективных полей и квадратичной магнитоупругой связи.
Ключевые слова: прецессия намагниченности, магнитоупругое взаимодействие, параметрический портрет.
Abstract. The forced nonlinear magnetization second order precession in normal magnetized plate having magnetoelastic properties is investigated. The orientation transition of magnetization vector which consists in variation of vector equilibrium position by magnetoelastic constant variation is analyzed. The equation system for equilibrium position of magnetization vector relative to magnetization and elastic displacement components which was resolved by Kardano method is found. The parametrical portraits for magnetization and elastic displacement are constructed. The role of magnetoelastic interaction in these portraits’ form is investigated on the basis of potential model. Two models was proposed for interpretation of precession period dependence from magnetoelastic constant value: effective fields and quadratic magnetoelastic connection.
Key words: magnetization precession, magnetoelastic interaction, parametrical portrait.
Введение
Нелинейные СВЧ колебания намагниченности в магнитных диэлектриках привлекают широкое внимание исследователей [1-4]. Амплитуда подобных колебаний ограничивается параметрическим возбуждением обменных спиновых волн [3-5]. Это ограничение отсутствует в геометрии нормально намагниченной ферритовой пластины, когда частота ферромагнитного резонанса (ФМР) совпадает с дном спектра обменных волн [6,7]. В таких условиях углы нелинейной прецессии намагниченности могут достигать весьма больших величин: в непрерывном режиме до 20-25 градусов [8,9], а в импульсном – до 50-60 градусов [10]. Некоторые возникающие при этом виды прецессии описаны в обзоре [11], где постоянное магнитное поле превышает поле размагничивания формы, то есть вектор намагниченности в равновесном состоянии ориентирован по нормали к плоскости пластины.
В постоянном поле, меньшем поля размагничивания, создаются условия ориентационного перехода, то есть равновесный вектор намагниченности отклоняется от нормали к плоскости пластины [12]. В этом случае под воздействием переменного поля само положение равновесия может начать прецессировать, так что возникает вынужденная прецессия намагниченности второго порядка [13,14]. При этом вектор намагниченности участвует одновременно в двух движениях прецессионного характера: в первом – вокруг положения равновесия, и во втором – вокруг направления поля. Период такой прецессии более чем на порядок превышает период возбуждающего поля, поперечные компоненты динамической намагниченности меняются по синусоидальному закону со сдвигом фаз на 90о, а прецессионный портрет имеет форму кругового кольца, равномерно заполненного вдоль образующей малыми кольцами [13,14].
В работе [15] выявлены пять различных режимов прецессии: №1 – малоамплитудная круговая прецессия, №2 – прецессия положения равновесия без охвата центра, №3 – незатухающая прецессия положения равновесия с охватом центра, №4 - затухающая прецессия положения равновесия с охватом центра, №5 – развернутая круговая прецессия. Переходы между режимами рассмотрены на основе трехмерной модели потенциала.
В работах [16,17] рассмотрены случаи несимметричного постоянного и переменного поля. Показано, что в этом случае прецессия положения равновесия приобретает характер импульсов неправильной формы, а на прецессионном портрете появляется четко выраженное сгущение малых колец. Местоположение сгущения на образующей большого кольца интерпретировано на основе векторной модели гиромагнитного характера.
В работах [18,19] прецессия положения равновесия была рассмотрена в среде с одноосной [18] и кубической [19] анизотропией. Показано, что анизотропные свойства среды, подобно асимметрии возбуждения и поля, приводят к импульсному характеру прецессии, результатом которого являются сгущения малых колец прецессионного портрета, отражающие пространственное расположение осей анизотропии.
Все перечисленные работы относятся к случаю чисто магнитной среды, не обладающей какими-либо другими свойствами. Однако хорошо известно, что в реальных магнитных материалах на поведении намагниченности в значительной степени может сказываться магнитострикция [20].
Так в работе [21] на примере пленок ферритов-гарантов показано, что магнитоупругое взаимодействие оказывает существенное влияние на ориентационный переход намагниченности, в частности, меняет поле перехода и характер установления намагниченности во времени.
В этом свете можно ожидать, что свойства магнитоупругости могут также каким-то образом изменять характер прецессии второго порядка. Настоящая работа посвящена выяснению этого вопроса.
1. Геометрия задачи
Подобно [22], рассмотрим ферритовую пластину, намагниченную по нормали к ее плоскости, в геометрии, показанной на рис.1.
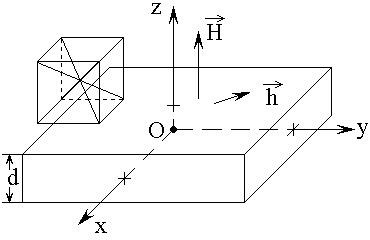
Рис.1. Геометрия задачи.
Будем полагать, что
феррит по магнитным свойствам – изотропен, однако по упругим и магнитоупругим
– обладает кубической симметрией, причем плоскость грани куба соответствует
плоскости ферритовой пластины (на рисунке показана схема кубической ячейки).
Подобно [22] будем считать, что упругие свойства описываются только константой
, а магнитоупругие – константой 
. Введем декартову систему координат 
, ось 
которой
перпендикулярна плоскости пластины. Пусть внешнее поле имеет вид: 
, где 
–
постоянное подмагничивающее поле, 
- компоненты
переменного поля, причем 
.
2. Плотность энергии
Полагая полную плотность
энергии пластины 
равной сумме плотностей
магнитной, упругой и магнитоупругой энергий, для случая кубической анизотропии
с ориентацией типа (100), оставляя только члены, важные для дальнейшего
рассмотрения, подобно [20, 23-26], получаем:
, (1)
где 
–
нормированный вектор намагниченности, 
–
намагниченность насыщения; 
– координаты, 
, 
–
тензор деформаций:
–
компоненты упругого смещения.
3. Основные параметры задачи
Для более рельефного
выявления основных особенностей прецессии второго порядка желательно рассмотреть
реальный материал, в котором магнитоупругое взаимодействие проявляется
достаточно сильно. В настоящей работе в качестве такового выбран тербиевый
феррит-гранат (ТбФГ), параметры которого следующие [24]: 
(по другим данным 
),
; 
; 
. Некоторые оценки будут выполнены также
для железоиттриевого граната (ЖИГ), константа магнитоупругого взаимодействия
которого равна [24]: 
. Толщину магнитной пластины
возьмем равной 1 мкм.
Для удобства построения
разверток колебаний во времени и прецессионных портретов, параметры затухания,
кроме особо оговоренных случаев, подобно [22], будут выбраны также несколько
завышенными по сравнению с таковыми для ЖИГ и ТбФГ: 
; 
.
В большинстве
рассматриваемых далее примеров постоянное поле будет принято равным 
, амплитуды переменного поля 
(поле круговое), частота переменного поля
, начальные значения компонент
намагниченности: 
, 
.
Остальные параметры задачи будут указаны по ходу текста.
В расчетах будет использована система СГС (Гаусса), так что некоторые формулы будут приведены без явного указания размерности, что сделано для сокращения формы записи.
4. Ориентационный переход в магнитоупругой среде
Некоторые особенности ориентационного перехода в присутствии магнитоупругости рассмотрены в работе [21]. Проведем здесь более подробное рассмотрение в аспекте, необходимом далее для интерпретации прецессии второго порядка.
Предположим, что
благодаря симметрии задачи (рис.1), вектор намагниченности всегда находится в
плоскости 
, то есть 
.
Положим, что пластина деформируется только в той же плоскости : отличны от нуля только 
и 
, то
есть 
. Для начала будем считать, что внешнее переменное
поле отсутствует: 
.
При этом плотность энергии (1) принимает вид:
В силу нормировки:
Подставляя (4) в (3), получаем:
В этом выражении имеются
две переменные: 
и 
,
поэтому для нахождения равновесного состояния надо приравнять к нулю его первые
производные по обеим этим переменным. В результате получаем систему для определения
и 
:
Выражая из (7):
и подставляя в (6), получаем
уравнение для определения :
Решение этого уравнения
дает зависимость от нуля до поля перехода. В
начале перехода при 
намагниченность ориентирована в
плоскости пластины и 
. При этом 
. Окончание перехода соответствует 
, то есть 
. Поле
перехода 
можно найти, подставляя в (9) значение , откуда получаем:
Из этой формулы видно,
что увеличение 
, уменьшение 
или 
приводят
к увеличению поля перехода.
Вводя обозначение «поля магнитоупругого взаимодействия»
получаем:
В отсутствие магнитоупругой связи поле перехода равно полю анизотропии формы пластины:
Разделяя (9) на , с обозначением (11) получаем:
В отсутствие
магнитоупругой связи при 
и 
в интервале 
,
определяемом условием 
, это уравнение имеет тривиальное
решение:
Однако при наличии магнитоупругой связи полное уравнение (9) является кубическим, для решения которого, в зависимости от соотношения коэффициентов, традиционно применяются два способа: формула Кардано и тригонометрическое решение [27,28]. В работе [21] для рассмотренного там случая показана правомерность использования решения Кардано. Рассмотрим здесь этот вопрос более подробно.
5. Возможность применения решения Кардано
Разделяя (14) на 
, получаем:
Вводя обозначения:
приводим уравнение (16) к каноническому виду:
Это – классическое «неполное» кубическое уравнение [27,28], способ разрешения которого определяется знаком его детерминанта:
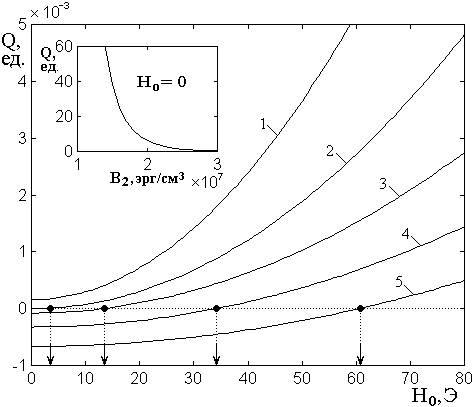
Обратимся к рис.2, где
показана зависимость детерминанта 
от поля 
при различных значениях константы магнитоупругого
взаимодействия 
.
Рис.2. Зависимость детерминанта
уравнения (19) от поля при различных значениях
константы : 1 – 
; 2 –
;
3 – 
; 4 –
; 5 – 
.
На врезке – зависимость детерминанта
от константы при 
.
Параметры – указаны в разделе №3.
Из рис.2 видно, что при
любых значениях константы зависимость от является
квадратичной параболой, как это и следует из вида второго слагаемого выражения
(20) с учетом (17) и (18). Однако из первого слагаемого того же выражения можно
видеть, что парабола смещается по вертикали вверх или вниз в зависимости от
соотношения между 
и 
.
На врезке показана
зависимость детерминанта от константы при 
, характеризующая пересечение кривых на
основном рисунке с его вертикальной осью. Из (20) с учетом (17) можно видеть,
что эта зависимость обратно пропорциональна полю магнитоупругого взаимодействия
в третьей степени, то есть вблизи нуля детерминант стремится к плюс бесконечности.
Однако, как можно видеть
из основного рисунка, при достаточно большом значении константы детерминант при становится
отрицательным, что происходит при 
за счет
отрицательности в этом случае выражения (17). Из условия 
можно определить «нижнее» критическое
значение константы магнитоупругого взаимодействия 
, ниже
которого детерминант вблизи становится отрицательным:
При принятых значениях параметров получаем:
.
То есть при константе
выше этого значения детерминант при всегда положителен.
В этом случае для решения уравнения (16) можно пользоваться решением Кардано [27,28], тогда как при константе меньше критической в малом поле это решение неприменимо.
Однако, как видно из рис.2,
при константе большей полученного нижнего критического значения, вблизи нуля
поля имеется область, где детерминант при 
тоже
отрицателен. При этом изменению знака соответствует
«верхнее» критическое значение константы магнитоупругого взаимодействия 
. Определить это значение можно из условия
, разрешив его относительно . Однако, как можно видеть из структуры
выражения (20) с учетом (17) и (18), условие приводит
относительно к полному кубическому уравнению:
Решение этого уравнения позволяет найти верхнее критическое
значение 
с помощью формулы (11). Однако получение
такого решения в аналитическом виде крайне громоздко, поэтому удобнее
подставить требуемые значения параметров задачи, после чего решить его в
численном виде. Так, подставляя и , из (22) получаем:
Решая это уравнение,
находим: 
, откуда получаем:
Таким образом, детерминант уравнения (16) всегда положителен в интервале значений константы магнитоупругости:
где определяется
выражением (21), а – решением уравнения (23). При
заданных здесь параметрах задачи интервал (25) принимает вид:
то есть как раз содержит в себе
константы для ТбФГ и ЖИГ.
С другой стороны, из
рис.2
видно, что «запрещенная» окрестность поля вблизи нуля сравнительно невелика.
Так при значении константы 
детерминант
становится положительным уже при поле 
, при 
положительность детерминанта достигается
при 
, при 
– при
и при 
– при
(эти значения показаны стрелками на горизонтальной
оси).
В настоящей работе
прецессия равновесного положения намагниченности исследуется при поле равном , что значительно превышает упомянутые величины.
Таким образом, можно полагать, что в условиях принятых параметров (как констант
материала, так и поля) использование решения Кардано вполне допустимо.
В аналитическом виде решение Кардано уравнения (16), полученное согласно [27,28] с учетом (17),(18),(20), имеет вид:
где:
При этом компонента 
определяется соотношением (4).
6. Общий характер полного решения
Общий характер поведения
корней уравнения (16) иллюстрируется рис.3, где показана зависимость от 
функции
представляющей собой левую часть
уравнения (16). Здесь 
и 
определяются
соотношениями (17) и (18), а входящее в них поле –
соотношением (11).
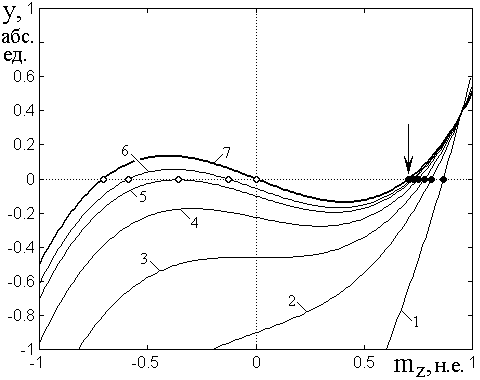
Рис.3. Функция 
при различных значениях константы :
1 – 
; 2 – 
; 3 – 
;
4 – 
; 5 –
; 6 – 
;
7 – 
.
Остальные параметры – те же, что на рис.2.
Из рис.3 видно, что
функция представляет собой кубическую параболу,
причем корни уравнения (16) определяются точками пресечения этой параболы с
горизонтальной осью, соответствующей 
(показана горизонтальной
точечной линией). Основные корни, соответствующие положительным значениям , показаны сплошными укрупненными точками.
Побочные корни обозначены открытыми точками. Видно, что все побочные корни
лежат в области отрицательных значений , то
есть, в силу четности задачи, реального физического смысла не имеют.
Парабола имеет только
один корень при 
(кривые 1 – 4). Именно условие
единственности действительного корня соответствует применимости решения
Кардано.
В то же время, кривые 1 и
2 лежат уже ниже интервала применимости решения Кардано (28), но все же точки
пересечения кривой с горизонтальной осью
существуют. Поэтому точные значения корней здесь должны быть получены с помощью
тригонометрического решения [27,28]. В настоящей работе такое решение не
проводилось, главным образом исходя из того факта, что значения константы для ТбФГ и ЖИГ лежат в интервале
применимости решения Кардано, то есть для реальных целей это решение является
достаточным.
Кривая 
, соответствующая 
,
уже почти касается горизонтальной прямой, то есть лежит вблизи верхней границы интервала
применимости решения Кардано (28).
При еще больших значениях
константы (кривые 6, 7) уравнение (16) имеет уже
три действительных корня, два из которых (открытые точки) лежат ниже 
, то есть физически не реализуются.
Из анализа соотношений (17)
и (18) с учетом (11) можно видеть, что при 
уравнение
(16) принимает вид:
отличное от нуля решение которого равно:
То есть при безграничном
увеличении константы компонента намагниченности принимает вполне определенное значительно
отличное от нуля значение (31). На рис.3 это значение отмечено стрелкой. При
этом кривая 7, построенная при 
, что в пределах
точности рисунка эквивалентно условию , представляет
собой асимптотический предел к которому стремится функция при безграничном увеличении константы .
По сплошным точкам на
рис.3 можно видеть, что уменьшение компоненты намагниченности по мере увеличения , сначала довольно быстрое (кривые 1-2),
постепенно замедляется (кривые 3-6), после чего останавливается (кривая 7).
Вследствие связи между
магнитной и упругой системами, пластина претерпевает при этом определенную
деформацию, существенным образом отличную от соответствующей равновесному
состоянию при 
. То есть в системе наступает определенная
«спонтанная деформация» [29,30], обусловленная взаимным влиянием магнитной и
упругой систем.
7. Магнитоупругая добавка к полю перехода
При типичных для ЖИГ
значениях параметров: 
, 
, 
, в соответствии с формулой (11) получаем:
, то есть добавка к полю перехода за счет
магнитоупругости составляет менее эрстеда и может существенно сказаться на поле
перехода только в его ближайшей окрестности.
Однако, благодаря
квадратичности по 
, уже при сравнительно небольшом
увеличении этой константы магнитоупругая добавка к полю перехода резко
возрастает. Так для тербиевого феррита-граната (ТбФГ) 
[24],
откуда получаем 
. Для материалов с меньшей, чем
у ЖИГ намагниченностью насыщения, к каковым относятся большинство
редкоземельных ферритов-гранатов, добавка к полю перехода еще более
увеличивается. Так для того же ТбФГ получаем: 
.
Поле перехода может
увеличиваться также при уменьшении константы 
,
характеризующей жесткость материалов. Для большинства твердых тел эта константа
имеет такой же порядок, что и для ЖИГ и ТбФГ (
),
однако для композиционных материалов может быть существенно меньше (в 10-20 раз
и более) [31]. То есть, если такие материалы будут обладать магнитными
свойствами, то для них добавка к полю перехода может составлять сотни и тысячи
эрстед.
8. Затягивание поля перехода за счет магнитоупругости
На основе полученного решения (28) уравнения (16) рассмотрим влияние магнитоупругого взаимодействия на поведение компонент намагниченности при ориентационном переходе.
Обратимся к рис.4, где
показаны зависимости компонент намагниченности (цифры
без штрихов) и (цифры со штрихами) от поля при различных значениях константы
магнитоупругого взаимодействия (рис.4а), а также
поясняющие их ход вспомогательные зависимости поля перехода от константы (б) и
нормированной плотности энергии 
от компоненты намагниченности
(в).
Из рис.4а видно, что в
начальном положении в отсутствие поля (
)
вектор намагниченности лежит в плоскости пластины: 
, 
. При увеличении поля происходит ориентационный переход,
состоящий в повороте вектора намагниченности к направлению поля. Переход
заканчивается при 
, 
, то
есть при выстраивании вектора намагниченности по нормали к плоскости пластины.
Кривые, пронумерованные
цифрами без штрихов, соответствуют зависимостям 
, со
штрихами – зависимостям 
. Возрастание номеров
кривых соответствует увеличению константы .
Кривые 1, 1/ соответствуют отсутствию магнитоупругой связи () и приведены здесь для сравнения.
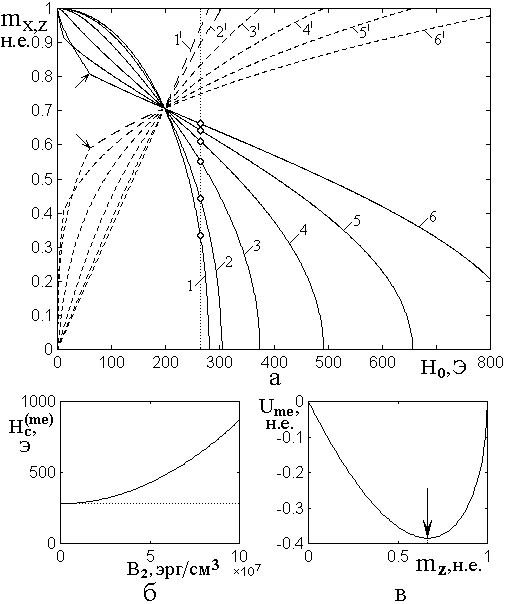
Рис.4. Затягивание поля перехода за счет магнитоупругого взаимодействия.
а – зависимости компонент вектора намагниченности (сплошные линии) и (пунктирные линии) от поля при различных значениях ;
б – зависимость поля перехода от
константы ;
в – зависимость нормированной плотности энергии 
от компоненты намагниченности .
Номера кривых: 1, 1/ – ; 2, 2/ – 
;
3, 3/ – 
; 4,
4/ – 
;
5, 5/ – 
; 6,
6/ – 
.
Из рассмотрения рис.4а
видно, что чем больше величина , тем сильнее переход
затянут по полю в сторону его увеличения. Так при 
переход
происходит при 
, что соответствует затягиванию
на 
, а при 
поле
перехода составляет уже 
(точка окончания
перехода находится за правым краем рисунка), то есть затягивание увеличивается
до 
.
Такой рост затягивания
соответствует квадратичному характеру зависимости поля перехода от в
соответствии с формулой (11), как это иллюстрируется рис.4б, где горизонтальная
точечная линия соответствует 
.
Таким образом, хотя
магнитоупругое взаимодействие увеличивает поле перехода на величину 
, зависящую от , но,
как это видно из рис.4а, все кривые 
проходят через одну и
ту же узловую точку. В этой точке продольная и поперечная компоненты вектора
намагниченности равны: 
, то есть вектор намагниченности
отклонен от нормали к пластине на 
, так что 
. Такое условие позволяет с помощью выражения
(16) найти поле узловой точки: 
, откуда при 
получаем: 
.
Из взаимного расположения
кривых на рис.4а видно, что до точки пересечения, то есть при 
, при наличии магнитоупругой связи нормальная
компонента намагниченности 
больше таковой в
отсутствие связи: кривые 2/ – 6/ проходят тем ниже кривой
1/, чем номер кривой (то есть константа )
больше. При этом касательная компонента 
соответственно
меньше: кривые 6 – 2 проходят тем ниже кривой 1, чем номер кривой больше.
Выше точки пересечения,
при 
, кривые меняются местами: при наличии
магнитоупругой связи нормальная компонента намагниченности становится меньше таковой в отсутствие связи,
а касательная компонента – больше, тем
заметнее, чем магнитоупругая связь выше (константа больше).
Такое взаимное расположение кривых можно понять, если рассмотреть последнее слагаемое в выражении для плотности энергии (5), которое представляет собой плотность энергии магнитоупругого взаимодействия:
При этом из второго
уравнения системы (6)-(7) можно видеть, что при любых значениях больших нуля, его удовлетворение требует
отрицательности величины 
. Таким образом, в
соответствии с (32), плотность энергии всегда
отрицательна. Вид нормированной на 
зависимости от величины показан
на рис.4в. Видно, что зависимость имеет минимум (показан стрелкой) как раз при 
(в точке экстремума функции (32)).
Таким образом, ниже 
(то есть при )
увеличение приводит к уменьшению энергии, в выше
(при 
) – к увеличению. То есть в первом случае
минимизация энергии требует увеличения , а во
втором – уменьшения, что и находит свое отражение в относительном расположении
кривых на рис.4а. При этом компонента , как
это следует из (4), ведет себя в точности обратным образом.
Из
рассмотрения зависимостей на рис.4а в области
малых значений поля можно видеть, что некоторые из них (5,5/, 6,6/)
претерпевают небольшой излом (точки излома для 6,6/ показаны
стрелками). Дополнительное исследование показывает, что этот излом как раз
соответствует полю, при котором детерминант Кардано (20) меняет знак, то есть
решение Кардано при меньших полях теряет силу. Для кривых 6 и 6/ это
поле равно , для кривых 5 и 5/ – , что как раз соответствует точкам
пересечения зависимостей 
на рис.2 (кривые 4 и
5) с горизонтальной точечной линией, соответствующей .
Можно видеть, что участки кривых на рис.4а, лежащие левее точки излома,
составляют их незначительную часть, даже при (кривые
6,6/), далеко не достигающую поля (отмеченного
вертикальной точечной линией), при котором в настоящей работе проводилось исследование
прецессии второго порядка. То есть сделанный в разделе №5 вывод о правомерности
использования решения Кардано, здесь полностью подтверждается.
9. Компоненты намагниченности
Главной задачей
проделанного рассмотрения ориентационного перехода является нахождение
равновесного положения вектора намагниченности в условиях магнитоупругого
взаимодействия. Поведение компонент намагниченности 
в
зависимости от величины константы иллюстрируется рис.5.
Из рис.5 видно, что по
мере увеличения константы магнитоупругого взаимодействия компонента намагниченности увеличивается, а компонента уменьшается. То есть по мере увеличения
магнитоупругого взаимодействия вектор намагниченности поворачивается ближе к
плоскости пластины. Открытые точки на зависимости 
соответствуют
открытым точкам на рис.4а. Видно, что в обоих случаях рост по мере увеличения постепенно замедляется. На рис.4а такое
замедление обусловлено уменьшением наклона кривых 1 – 6 из-за увеличения
затягивания поля перехода , что в свою очередь
связано с квадратичностью зависимости поля от (11) , как это показано в разделе №11, а
также иллюстрируется врезкой на рис.5.
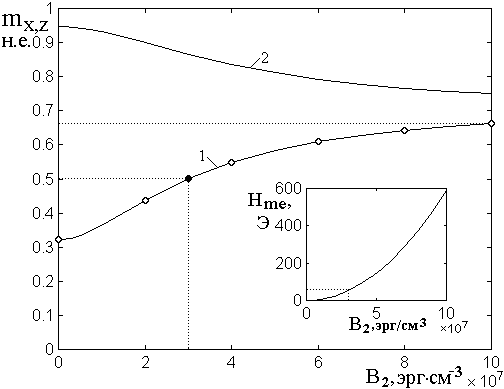
Рис.5. Зависимости равновесных
компонент намагниченности (1) и (2) от константы магнитоупругого
взаимодействия при поле .
На врезке – зависимость поля
магнитоупругого взаимодействия от константы .
В отсутствие
магнитоупругой связи (при ) компоненты намагниченности
равны: 
, 
Случаю
тербиевого феррита-граната соответствует сплошная точка при 
, при этом: 
, 
Константе соответствуют
компоненты 
, 
Из рис.5 видно, что обе
кривые 1 и 2 при увеличении за правым краем
рисунка имеют тенденцию сомкнуться, что будет соответствовать равенству 
. То есть изменение компоненты по мере увеличения (кривая 2), быстрое при малых значениях
константы, замедляется и совсем останавливается при . Из
условия нормировки (4) можно видеть, что при этом обе компоненты
намагниченности равны 
, что соответствует отклонения
вектора намагниченности от плоскости пластины на угол равный .
Как показано в разделе №6,
именно такое поведение компоненты соответствует полному решению
уравнения (16), при приводящему к спонтанной деформации
пластины, отсутствующей в случае .
10. Поперечная компонента упругого смещения
Найдем теперь поперечную
компоненту упругого смещения, сопровождающего рассмотренное в предыдущем
разделе равновесное значение намагниченности при ориентационном переходе. Подобно
работе [22], ограничимся компонентой 
, так как симметрия
задачи приводит к аналогичности динамических свойств компонент и 
с
точностью до изменения фазы на 
.
Так для стационарного состояния из формулы (8) с учетом (4), получаем:
Согласно предположениям, принятым далее в разделе №11 относительно динамического упругого смещения, имеет место соотношение:
то есть:
Учитывая независимость
намагниченности от координаты 
, для смещения на
поверхности пластины при 
, получаем:
Здесь интегрирование
производится по верхней половине магнитной пластины, так как начало координат,
от которого отсчитывается смещение , выбрано в центре ее
толщины. Соответственно при интегрировании по нижней половине пластины получится
такое же смещение, которое, однако, в предположении неподвижности центральной
плоскости пластины, будет иметь противоположный знак. То есть, если центральную
плоскость пластины считать неподвижной относительно начала координат, то
противоположные ее поверхности, будучи свободными, будут двигаться в
противоположных направлениях.
Более подробно этот вопрос расмотрен в работах [32,33], где показано, что благодаря антифазности упругих колебаний на противоположных поверхностях пластины, при закреплении одной из поверхностей, амплитуда упругих колебаний на свободной поверхности удваивается (формула (77) в [33]).
Заметим, что полученное соотношение (36) соответствует равновесному положению намагниченности в стационарном состоянии при ориентационном переходе. Правомерность его применимости к динамическому режиму будет отмечена в разделе №13.
11. Уравнения движения
Для исследования свойств прецессии намагниченности второго порядка в магнитоупругой среде воспользуемся аппаратом, развитым в работах [13-19], модифицируя его с учетом магнитоупругости.
Так уравнения движения для намагниченности Ландау-Лифшица с диссипативным членом в форме Гильберта имеют вид [1,21,22]:
; (37)
; (38)
; (39)
где 
–
гиромагнитная постоянная (
), 
– параметр затухания прецессии
намагниченности.
Расчет входящих в эти уравнения эффективных полей проведем в тех же предположениях, которые первоначально были приняты в работе [22], а также использовались в работах [13-19].
Во-первых, будем считать, что прецессия намагниченности в пластине является однородной, то есть от координат не зависит.
Во-вторых, предположим,
что продольные колебания вдоль оси с намагниченностью не
связаны, то есть можно полагать 
.
Для расчета эффективных полей воспользуемся классической формулой [1]:
где 
–
плотность энергии, определяемая формулой (3).
Эффективные поля с учетом принятых предположений принимают вид:
Уравнения для упругого смещения имеют вид:
где 
–
параметр затухания упругих колебаний, 
–
плотность материала пластины.
Граничные условия на поверхностях пластины следующие:
Система (37)-(39), (44)-(45) с учетом (46)-(47) решалась численно методом Рунге-Кутта четвертого порядка [28], рассматривалось развитие вынужденных колебаний намагниченности во времени. При расчете использовались параметры, приведенные в разделе №3.
12. Развитие колебаний во времени и параметрические портреты для намагниченности
Рассмотрим теперь, какую
специфику вносит магнитоупругое взаимодействие в прецессию намагниченности
второго порядка. В качестве основных объектов исследования изберем развитие
колебаний во времени, а также взаимное соотношение между поперечными (
и 
)
компонентами намагниченности и смещения (параметрические или прецессионные
портреты).
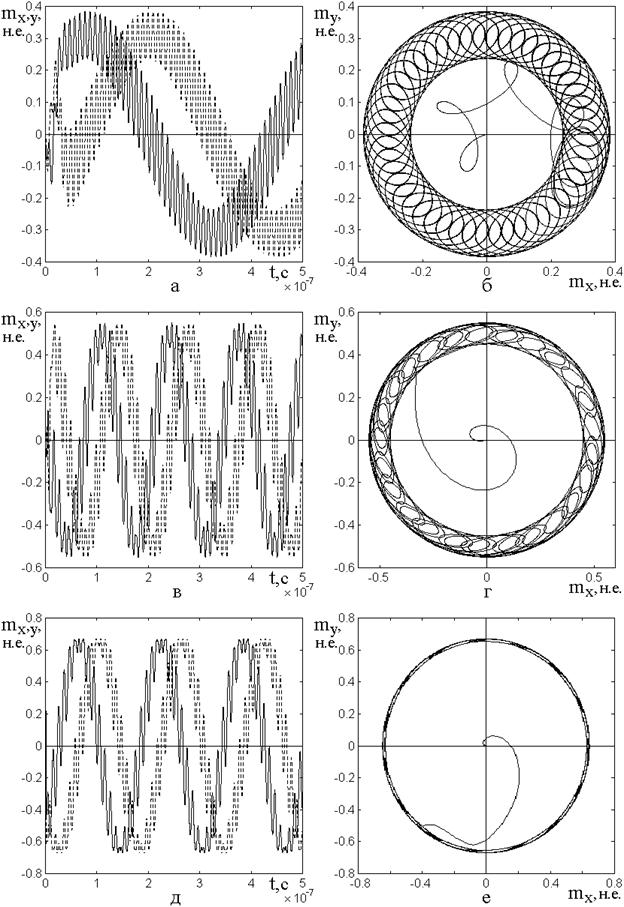
Обратимся к рис.6, где в
левом столбце показаны зависимости поперечных компонент намагниченности (сплошные линии) и 
(пунктир)
от времени (а,в,д), а в правом – параметрические прецессионные портреты, то
есть зависимости компоненты от компоненты , когда время является параметром.
Зависимости построены при различных значениях константы магнитоупругости. Рис.6а
и 6б соответствуют отсутствию магнитоупругой связи () и
приведены здесь для сравнения. Пары рисунков 6в,г и 6д,е соответствуют
значениям константы магнитоупругости 
(значение, типичное
для тербиевого феррита-граната) и 
(увеличенное примерно
в три раза).
Из рисунка видно следующее.
Как и в отсутствие магнитоупругости колебания намагниченности имеют две составляющие: быструю, синхронную с возбуждающим полем, и медленную с периодом во много раз меньшим. Такое двухпериодическое движение, впервые подробно рассмотренное в работе [13], является характерным свойством прецессии положения равновесия.
Медленные колебания
компонент намагниченности 
и 
сдвинуты по фазе относительно друг друга
на 
, что также неоднократно отмечалось в
работах [13,14].
Из рис.6а,в,д (с учетом
масштаба по вертикальной оси) можно видеть, что при увеличении константы
магнитоупругого взаимодействия амплитуда колебаний обеих компонент
намагниченности увеличивается. Так она составляет 
, при равна
, а при достигает
Рис.6. Зависимости поперечных
компонент намагниченности (сплошная линия) и (пунктир) от времени (а,в,д), а также прецессионные
портреты – зависимости компоненты от компоненты (б,г,е), при различных значениях константы
магнитоупругости.
а,б – ; в,г
– ; д,е – .
Из рис.6б,г,е видно, что
при увеличении константы магнитоупругого взаимодействия диаметр большого кольца
прецессионного портрета увеличивается, а его ширина уменьшается. Так при внутренний радиус кольца равен 
, внешний – , то
есть ширина кольца равняется 
При этом средний радиус
кольца равен 
При радиусы
кольца равны
и , а
ширина – 
Средний радиус – 
При
эти величины равны соответственно 
, и 
Средний радиус – 
Сравнение наблюдаемых
средних радиусов колец со значениями компоненты намагниченности (рис.5) при тех же значениях константы , показывает их совпадение с точностью не
хуже 
от средней величины.
То есть можно считать, что средний радиус больших колец прецессионного портрета определяется равновесным значением поперечной компоненты намагниченности, определяемым соотношением между приложенным постоянным полем и параметрами материала пластины.
Подробное рассмотрение
показывает, что описанные в этом разделе свойства прецессии второго порядка
имеют место во всем диапазоне значений константы магнитоупругости, вплоть до 
. Дальнейшее увеличение вплоть до 
приводит
к еще большему уменьшению ширины больших колец, а также к квадратичной
зависимости периода медленных колебаний от константы ,
более подробно рассмотренной в разделе №18.
13. Развитие колебаний во времени и параметрические портреты для упругого смещения
Рассмотрим теперь колебания упругого смещения, сопровождающие описанные в предыдущем разделе колебания намагниченности.
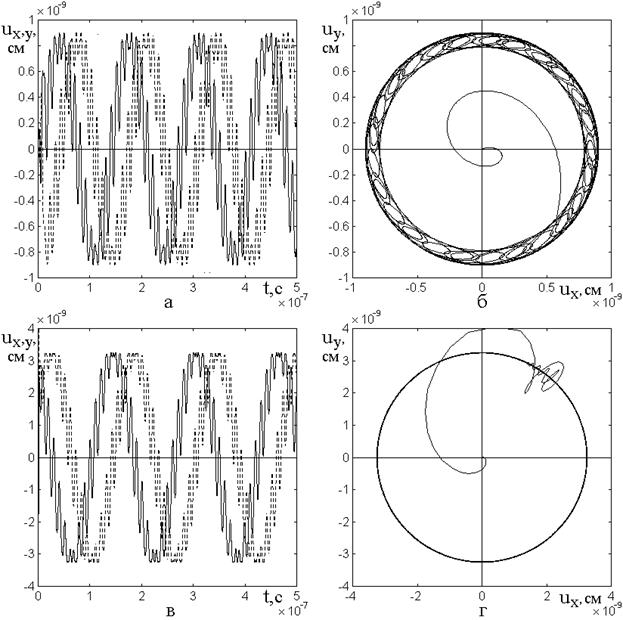
Рис.7. Зависимости поперечных
компонент упругого смещения 
(сплошные линии) и 
(пунктир) от времени (а,в), а также
параметрические портреты смещения – зависимости компоненты от компоненты (б,г),
при различных значениях константы магнитоупругости.
а,б – ; в,г
– .
На
рис.7 показаны зависимости поперечных компонент упругого смещения (сплошные линии) и (пунктир) от времени (а,в), а также
параметрические портреты смещения – зависимости компоненты от компоненты (б,г)
(аналог прецессионного портрета для намагниченности), при значениях константы
магнитоупругости, соответствующих таковым, принятым при построении рис.6.
Из рисунка видно следующее.
Колебания компонент упругого смещения в общем синхронны колебаниям компонент вектора намагниченности, причем упругие колебания, как быстрые, так и медленные, находятся в противофазе относительно магнитных.
Подобная противофазность, по-видимому, является общим свойством упругих колебаний, сопровождающих прецессию намагниченности. Для простой прецессии, в том числе сильно нелинейной, это свойство прослеживается из рассмотрения рис.2 в работе [22].
С другой стороны, для стационарного состояния из формулы (36) следует, что координатная составляющая упругого смещения обратна по знаку соответствующей компоненте намагниченности.
Таким образом, наблюдаемая на рис.7 противофазность упругих колебаний относительно магнитных, является подтверждением выполнения соотношения (36) не только в статике, но и в динамическом режиме.
Из рис.7а,в (с учетом
масштаба по вертикальной оси) можно видеть, что при увеличении константы
магнитоупругого взаимодействия амплитуда колебаний обеих компонент упругого
смещения увеличивается. Так при (рис.7а) она равна 
, а при (рис.7б)
достигает 
. Такое увеличение сходно аналогичному
увеличению амплитуды колебаний намагниченности при том же увеличении (рис.6б,в), однако здесь оно заметно
больше: для намагниченности – в 
раз, для упругого
смещения – в 
раза.
Такое различие,
по-видимому связано с тем, что поперечная компонента намагниченности при
увеличении возрастает нелинейно: ее рост постепенно
замедляется, ограничиваясь условием постоянства длины вектора намагниченности.
В то же время, для упругого смещения в принятых рамках закона Гука такое
ограничение отсутствует, так что упругое смещение может увеличиваться прямо
пропорционально увеличению , как это и видно из формулы
(36).
Увеличение амплитуды медленных
колебаний упругого смещения при увеличении проявляется
в увеличении диаметра большого кольца параметрического портрета на рис.7б,г.
Уменьшение ширины кольца здесь аналогично подобному уменьшению для намагниченности. При этом из сохранения амплитуды быстрых колебаний, наблюдаемого на рис.7а,в, следует эллиптичность малых колец параметрического портрета для упругости (рис.7б,г), аналогичная подобной эллиптичности для намагниченности (рис.6г,е).
Расчет амплитуды упругого
смещения при заданной компоненте намагниченности , выполненный по формуле (36), дает при значение 
, а
при – 
.
Можно видеть, что эти значения довольно хорошо (с точностью не менее ) совпадают с наблюдаемыми радиусами
параметрических портретов на рис.7б и рис.7г – и соответственно.
Столь хорошее совпадение дополнительно подтверждает правомерность использования формулы (36) в динамическом режиме, а также полностью доказывает соответствие упругих колебаний вызывающим их магнитным.
14. Характеристики колебаний при различной степени магнитоупругой связи
Рассмотрим теперь
основные характеристики магнитных и упругих колебаний при различной величине
магнитоупругой связи, для чего обратимся к рис.8. Точки, приведенные на рисунке
– результат машинного эксперимента, линии построены, исходя из плавного
соединения точек. Все графики соответствуют интервалу изменения от нуля до значения 
, выше которого приведенные здесь
зависимости вплоть до 
(за правым краем рисунков),
сохраняют ту же тенденцию изменения (не приведены для обеспечения достаточно
крупного масштаба начальных участков кривых, где изменения наиболее сильные).
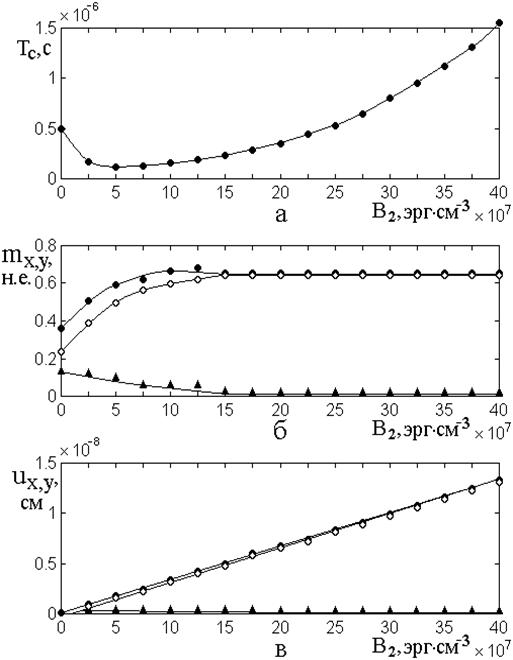
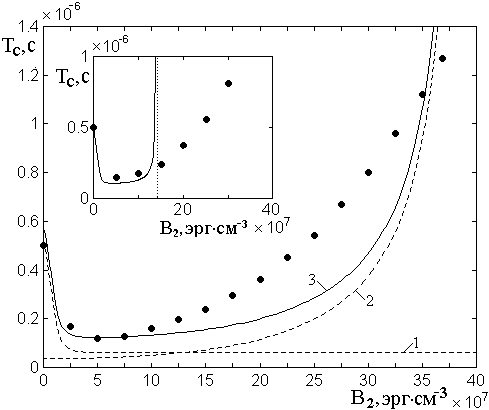
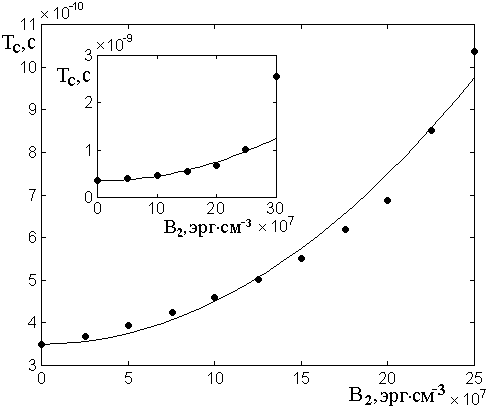
На рис.8а показана
зависимость периода медленных колебаний 
от величины
константы магнитоупругого взаимодействия . Можно
видеть, что сразу же при включении магнитоупругого взаимодействия период
колебаний резко уменьшается. Спад периода продолжается от нуля до 
, после чего период возрастает сначала
медленно до , а затем все быстрее вплоть до конца
исследованного диапазона .
Такой характер изменения
периода, по-видимому, говорит о наличии двух противоборствующих механизмов,
один из которых приводит к уменьшению периода при увеличении , а второй – к его увеличению. Более
подробно этот вопрос будет рассмотрен в разделах №16-18.
На рис.8б показаны для
компонент намагниченности зависимости внешнего (сплошные точки) и внутреннего
(открытые точки) радиусов большого кольца прецессионного портрета, а также
разности между ними (треугольники), то есть ширины кольца, от величины
константы .
Рис.8. Период колебаний (а) и характеристики колец параметрических портретов для намагниченности (б) и упругого смещения (в) при различных значениях магнитоупругой связи.
Сплошные точки на рис.8б,в – наружный радиус большого кольца портрета, открытые точки – внутренний радиус, треугольные точки – ширина большого кольца портрета.
Видно, что по мере
увеличения как внешний, так и внутренний радиусы
кольца сначала до 
увеличиваются, после чего
принимают стационарное значение вблизи 
Такое
поведение соответствует увеличению равновесного отклонения вектора намагниченности
от нормали к плоскости пластины (от оси 
) по
мере увеличения константы , то есть увеличению
компонент 
, до величины порядка 
, в соответствии с показанным их ходом на
рис.5 (кривая 1).
Из нижней кривой на рис.8б
(треугольники) видно, что ширина большого кольца по мере увеличения плавно уменьшается, стремясь к весьма
малому значению (порядка 
и менее). Это не означает
однако сужения малого кольца по всем диаметрам. Как можно видеть из рис.6а,в,д,
амплитуда малых колебаний, синхронных с возбуждающим полем, при увеличении остается практически постоянной (порядка 
). То есть малое кольцо не сужается по
всему диаметру, а превращается в эллипс, вытянутый вдоль образующей большого
кольца, причем большая ось эллипса остается близкой к своему начальному
значению (или даже несколько больше, на 
),
соответствующему (рис.6а). Причина такой
деформации малого кольца будет обсуждена в разделе №15.
На рис.8в для компонент
упругого смещения показаны зависимости внешнего (сплошные точки) и внутреннего
(открытые точки) радиусов большого кольца параметрического портрета, а также
разности между ними (треугольники), то есть ширины кольца, от величины
константы . Видно, что здесь по мере увеличения как внешний, так и внутренний радиусы
кольца, начиная от нуля, соответствующего , во
всем интервале изменения увеличиваются по
линейному закону. Такое увеличение обусловлено прямой пропорциональностью
компоненты упругого смещения (а также ) константе , как
это видно из формулы (36).
Сужение кольца, отражаемое нижней кривой на рис.8в (треугольники), также происходит через превращение малых колец в эллипсы, вытянутые вдоль образующей большого кольца (что видно из рис.7а,в). Это сужение аналогично предыдущему случаю (рис.8б), то есть здесь упругое смещение просто повторяет (с соответствующим коэффициентом) то сужение, которое уже имеет место для намагниченности.
15. Деформация большого кольца при изменении магнитоупругой связи
Как уже отмечалось в
разделах №12-13, а также наблюдается на рис.6б,г,е, 7б,г и 8б,в, при увеличении
константы магнитоупругого взаимодействия диаметр
большого кольца параметрического портрета увеличивается, а его ширина
уменьшается. Рассмотрим теперь этот вопрос более подробно, а именно, покажем,
что оба эти свойства обусловлены изменением потенциальной энергии пластины при
изменении константы . Ограничимся рассмотрением
только намагниченности, так как, согласно показанному в разделе №13, а также
видно из работы [22], упругое смещение повторяет поведение вектора намагниченности
с точностью до постоянного коэффициента.
Плотность потенциальной
энергии рассматриваемой задачи, выраженная через продольную компоненту
намагниченности , имеет вид (5). Прецессионные
портреты (рис.6б,г,е) содержат только поперечные компоненты намагниченности и 
,
причем благодаря симметрии геометрии задачи, роль этих компонент также
полностью симметрична. Поэтому достаточно рассмотреть только одну компоненту,
например .
Следуя условию сохранения длины вектора намагниченности (4), выразим плотность потенциальной энергии (e33) через эту компоненту:
. (48)
В равновесном состоянии
компонента тензора деформаций (33), выраженная
через , имеет вид:
Подставляя (49) в (48), получаем:
Полученное выражение
позволяет найти зависимость плотности энергии от . Его
минимум будет соответствовать равновесному состоянию намагниченности,
обусловленному как внешним полем с учетом размагничивания
, так и упругими, а также магнитоупругими
свойствами материала пластины через посредство констант 
и
.
Обратимся теперь к рис.9,
где показаны зависимости плотности потенциальной энергии пластины от поперечной
компоненты намагниченности построенные по формуле (50) при различных значениях
константы .
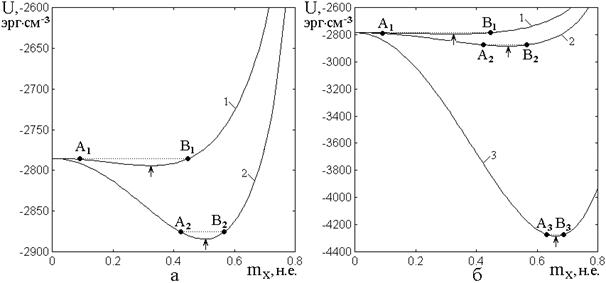
Рис.9. Зависимости потенциала от поперечной
компоненты намагниченности при различных значениях константы .
а – крупный масштаб, б – мелкий масштаб.
1 – ; 2 – 
; 3 –
.
Кривая 1 соответствует
отсутствию магнитоупругой связи и приведена здесь для сравнения, кривые 2 и 3
соответствуют двум значения константы : 
и 
, то
есть тем, же, что использовались при построении прецессионных портретов на рис.6г,е.
Стрелками снизу показаны
минимумы кривых, соответствующие равновесному положению намагниченности. Точки,
обозначенные буквами 
, 
, а
также соединяющие их горизонтальные точечные линии, соответствуют равным
значениям потенциала на фиксированной высоте относительно минимума, равной 
. Для повышения наглядности рисунка, чтобы
горизонтальные линии не сливались с минимумами, это значение высоты завышено
по сравнению с реальным, имеющим место на рис.6, примерно в два раза.
Упомянутое значение
высоты обеспечивается уровнем возбуждения (полем 
) и
сохраняется постоянным при любом значении , то
есть для всех трех кривых. При таком заданном уровне энергии, обеспечиваемым
полем возбуждения, компонента намагниченности колеблется
в потенциальной яме, ограниченной точками и.
Ширина такой ямы, то есть
расстояние между ее крайними точками, соответствует ширине большого кольца
прецессионного портрета. Видно, что 
, то есть ширина кольца
по мере увеличения константы сужается, как это и
следует из рис.6.
С другой стороны, можно
видеть, что по мере увеличения положения минимумов
кривых смещаются в сторону больших значений . Это
также полностью соответствует отмеченному на рис.6 увеличению диаметра большого
кольца.
Таким образом, можно полагать, что рассмотренная модель потенциала описывает свойства большого кольца прецессионного портрета полностью адекватно.
16. Период медленных колебаний при изменении магнитоупругой связи
Рассмотрим теперь другую
важную характеристику прецессии второго порядка, а именно: период медленных
колебаний при различной величине магнитоупругой связи. Основная зависимость
показана на представленном в разделе №14 рис.8а, где видно, что по мере
увеличения константы период сначала
резко уменьшается, после чего, пройдя через минимум, все быстрее увеличивается.
Там же отмечено, что причиной такого поведения периода может явиться
конкуренция двух механизмов, один из которых стремится период уменьшить, а
другой – увеличить. Рассмотрим такие механизмы на основе моделей эффективных
полей и квадратичной магнитоупругой связи.
17. Модель эффективных полей
При построении модели эффективных полей будем отталкиваться от результатов работ [13,14], выполненных в отсутствие магнитоупругой связи.
На основе векторной модели там показано, что период медленных колебаний определяется выражением:
причем 
, где 
– близкий к единице постоянный коэффициент,
определяемый параметрами материала. Для случая, рассмотренного в работе [13],
показано, что 
, здесь же для простоты будем считать
.
В этой формуле под 
понимается внешнее переменное поле,
которое по отношению к колебаниям намагниченности является возбуждающим.
В магнитоупругой системе упругие колебания возбуждаются за счет магнитных, после чего сами создают определенные магнитные поля, которые также воздействуют на намагниченность. Таким образом имеет место самосогласованный процесс, в случае обычной прецессии первого порядка приводящий к выравниванию времени релаксации магнитных и упругих колебаний даже в том случае, если изначально такие времена для каждой из систем были различными [22].
Положим теперь, что в
связанной магнитоупругой системе роль внешних полей играют
эффективные поля 
, определяемые выражениями (41)-(42).
При этом формула (51) для периода принимает вид:
где учтена симметрия задачи
относительно и .
Подставляя
равновесное значение , определяемое формулой (33),
получаем:
Из этой формулы видно,
что при увеличении период прецессии второго
порядка должен уменьшаться.
В то же время, такое
поведение периода никак не отражает его рост при достаточно больших значениях , наблюдаемый в правой части рис.8а.
Здесь, чтобы быть достаточно последовательным, надо предположить, что не только
внешнее поле заменяется на эффективное 
(41), но и другое внешнее поле также заменяется на эффективное поле 
(43). При этом период, с учетом равновесного
состояния (33), принимает вид:
Здесь уже видно, что
увеличение может обеспечить не только рост Tc, но и расходимость при стремлении
подкоренного выражения к нулю.
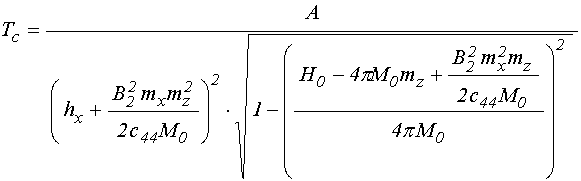
Формула (54) дает величину периода как произведение действия двух механизмов эффективных полей. Однако подробное рассмотрение показывает, что более соответствующим наблюдаемым результатам является не произведение, а суммарное действие каждого из эффективных полей по отдельности, то есть период должен иметь вид:
где:
Замечание. Как показано в разделе №5, входящие
в эти формулы значения компонент намагниченности и получаются с помощью решения Кардано (28),
которое при принятых здесь параметрах справедливо только при 
. Однако, как можно видеть из хода кривой
5 на рис.3, значение при 
отличается
от соответствующего менее чем на доли процента, а
при последующем увеличении это различие еще более
уменьшается. То есть при 
формулами (56)-(57)
можно пользоваться с достаточной степенью точности, полагая в них сразу 
, что соответствует (31).
Рассмотрим теперь рис.10, где показаны зависимости периода медленных колебаний намагниченности от величины константы магнитоупругого взаимодействия построенные по различным приведенным здесь формулам.
Рис.10. Зависимость периода медленных колебаний намагниченности от величины константы магнитоупругого взаимодействия по модели эффективных полей.
Формулы построения кривых: 1 – (59); 2 – (60); 3 – (61).
На врезке – зависимость, построенная по формуле (58).
Точки – те же, что на рис.8а.
Численный расчет по
формулам (55)-(57) с использованием приведенных здесь параметров материала
(раздел №3), действительно дает сначала резкий спад зависимости 
, после чего плавный подъем с последующей
расходимостью. Однако уже при 
период увеличивается
настолько, что стремится к бесконечности. Этому случаю соответствует зависимость,
показанная на врезке, для построения которой использовалась формула:
Здесь постоянный
коэффициент 
при 
, нормирующий
множитель 
, введен для того, чтобы согласовать ход
зависимости (58) при 
. Коэффициент 
при 
настолько
близок к единице, что вносимое им уточнение можно считать находящимся в
пределах точности машинного эксперимента.
Видно, что хотя
приведенная на врезке кривая качественно довольно хорошо отражает наблюдаемую
зависимость, однако имеет место определенное количественное расхождение: чрезмерно
ранняя расходимость , соответствующая значению , меньшему наблюдаемого примерно в три
раза.
Для более точного согласования расчетных кривых с наблюдаемыми зависимостями были введены поправочные коэффициенты, результат действия которых приведен на основном рис.10. Здесь кривая 1 (пунктирная) построена по формуле:
кривая 2 (пунктирная) – по формуле:
причем по горизонтальной оси введено
растяжение масштаба, для чего в формуле (57) величина заменена
на 
. Кривая 3 (сплошная) построена как сумма
этих двух кривых, то есть по формуле:
Можно видеть, что
полученная кривая в области малых значений довольно
близко соответствует наблюдаемым точкам, а при достаточно больших значениях отражает стремление периода к
бесконечности. Однако в области средних значений 
кривая
3 проходит ниже наблюдаемых точек, причем различие достигает полутора-двух раз.
Таким образом, модель эффективных полей позволяет качественно, а с учетом поправочных коэффициентов также и количественно, объяснить два свойства зависимости периода от константы магнитоупругого взаимодействия: резкий спад при малых ее значениях и постепенный рост при больших. Однако при промежуточных значениях константы модель дает заметно заниженные результаты.
Кроме того,
дополнительное исследование показывает, что несмотря на рост периода при
увеличении, расходимость вплоть до 
как таковая не наблюдается, то есть
период увеличивается значительно и рост его ускоряется, но все же не достигает бесконечности
(то есть экспериментальная кривая (точки) в своем движении вертикальной
асимптоты не имеет). Более подробно этот вопрос рассмотрен в разделе №18.
Такое обстоятельство, в первую очередь необходимость растяжения горизонтального масштаба в формуле (57), побуждает обратиться к рассмотрению других возможных механизмов формирования наблюдаемых зависимостей.
18. Модель квадратичной магнитоупругой связи
Как показано в предыдущем
разделе, модель эффективных полей достаточно хорошо описывает поведение периода
при малых и больших значениях , поэтому здесь
обратимся к рассмотрению случая средних значений , при
которых спад периода при увеличении уже прекращен, а предсказываемая
этой моделью расходимость еще не наступает, то есть в интервале: 
.
В качестве основного
физического положения учтем, что пластина с магнитоупругой связью представляет
собой совокупность двух связанных колебательных систем – магнитной и упругой.
Связь осуществляется через посредство магнитоупругости, описываемой константой . Приложенное переменное поле возбуждает
магнитную систему, откуда часть энергии возбуждения передается упругой системе.
То есть можно считать, что упругая система как бы нагружает магнитную, приводя при достаточной величине связи к увеличению ее инерционности, а следовательно и к увеличению периода свободных колебаний, каковыми являются медленные колебания положения равновесия намагниченности.
Говоря образно, легкая магнитная система таскает за собой тяжелую упругую, в результате чего их совокупное движение замедляется.
В качестве иллюстрации воспользуемся механической векторной моделью, предложенной в работе [16, рис.4], где положение равновесия намагниченности рассматривается как самостоятельный вектор, который прецессирует вокруг направления постоянного поля. К такой системе применимы законы гироскопического движения [34], а именно, частота прецессии определяется формулой:
где 
–
момент силы, 
– момент количества движения.
Учитывая, что момент
количества движения пропорционален совокупной массе составляющих тело частиц,
можно видеть, что период прецессии, обратный величине 
,
с точностью до постоянного коэффициента, равен:
где 
–
эквивалентная масса прецессирующего тела.
Так как момент силы определяется действием приложенного переменного
поля на намагниченность, то есть от состояния упругой системы не зависит, можно
полагать, что период прецессии равновесного положения намагниченности с точностью до постоянного коэффициента
пропорционален только «эффективной массе» магнитной системы. Полагая, что эта
масса за счет взаимодействия с упругой системой увеличивается, можно
предположить, что период пропорционален
константе в какой-то не известной заранее степени.
В случае линейного увеличения массы степень будет первая, в случае нелинейного
– может быть более высокой.
Для того, чтобы
определить показатель степени более точно, в качестве вспомогательной задачи
обратимся к рассмотрению простой прецессии намагниченности в магнитоупругой
системе, когда постоянное магнитное поле превышает поле размагничивания, так
что вектор намагниченности в равновесном состоянии ориентирован точно вдоль оси
.
Иллюстрацией решения
такой задачи является рис.11, где показана зависимость периода свободной
прецессии намагниченности от величины магнитоупругой связи. Рассмотрена
свободная прецессия в условиях слабого магнитного (
) и полностью
отсутствующего упругого (
) затухания. Для
заведомой линейности задачи начальное значение поперечной компоненты
намагниченности выбрано равным 
.
Точки получены при решении задачи, аналогичной рассмотренной в работе [22]. Сплошная линия построена по формуле:
где коэффициент 
и постоянное слагаемое 
выбраны, исходя из условия максимального
совпадения кривой с рассчитанными точками.
Рис.11. Зависимость периода свободной прецессии намагниченности от константы магнитоупругого взаимодействия.
На врезке – та же зависимость в
большем интервале значений
Параметры: 
;
; 
; ; 
,
остальные параметры – совпадают с приведенными в разделе №3.
Из рис.11 видно, что
зависимость периода свободной прецессии от константы описывается
квадратичной функцией с довольно высокой точностью. Так максимальное
расхождение, имеющее место в области 
, составляет всего
около 
, а в области 
– не
более 
, причем эти расхождения имеют противоположные
знаки.
Таким образом, в качестве рабочего предположения можно считать, что период прецессии положения равновесия также описывается квадратичной функцией, подобной (64), при условии подбора соответствующих коэффициентов.
Замечание. Заметим, что для свободной
прецессии при 
наблюдается быстрый рост
величины периода, квадратичной функцией уже не описываемый. Так при 
рассчитанная по формуле (64) кривая
проходит ниже измеренных точек примерно в два раза, как это показано на врезке
рис.11. Однако можно полагать, что в этой области уже наступает рост периода,
описываемый моделью эффективных полей в соответствии с формулой (57). То есть в
этом случае период, по-видимому, может стремиться к бесконечности, отражая описываемую
этой моделью расходимость. Однако, для целей дальнейшего рассмотрения, будем
полагать, что в основном интервале изменения константы ,
величина периода описывается все же квадратичной функцией.
Рассмотрим теперь
возможность применения квадратичной функции к зависимости периода от для случая прецессии положения
равновесия.
Обратимся к рис.12, где показана зависимость периода медленных колебаний намагниченности от величины константы магнитоупругого взаимодействия по модели квадратичной магнитоупругой связи.
Здесь кривая 1 (пунктир) отражает влияние поперечной составляющей намагниченности и построена по модели эффективных полей (раздел №17) с помощью формулы (59) с учетом (56), то есть аналогична кривой 1 на рис.10. Здесь однако введена несколько большая постоянная добавка, что обусловлено началом кривой 2 от нуля, то есть:
Кривая 2 построена по формуле:
полученной в соответствии с моделью квадратичной магнитоупругой связи и аналогичной формуле (64) с точностью до замены постоянных коэффициентов. Как видим, здесь введение постоянной добавки, аналогичной второму слагаемому формулы (64), необходимым не является.
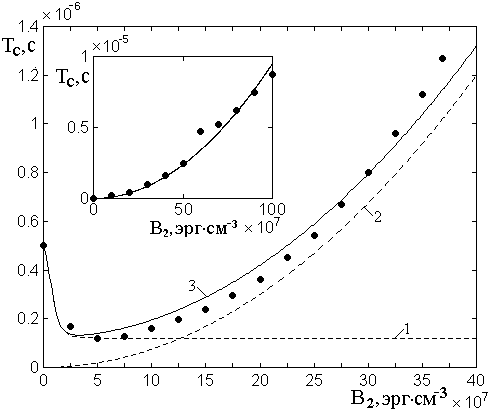
Рис.12. Зависимость периода медленных колебаний намагниченности от величины константы магнитоупругого взаимодействия по модели квадратичной магнитоупругой связи. Формулы построения кривых: 1 – (65); 2 – (66); 3 – (67). На врезке – зависимость, построенная по формуле (68).
Точки – те же, что на рис.8а.
Кривая 3 (сплошная) является суммой кривых 1 и 2, то есть соответствует формуле:
Из хода кривой 3 можно
видеть, что она в области отклоняется от
расчетных точек примерно на 
, а в области 
– не более чем на , причем эти отклонения имеют разные
знаки. В промежуточной же области, то есть около , где
отклонение меняет знак, можно считать совпадение практически точным.
Таким образом, здесь соответствие кривой 3 точкам значительно лучше, чем аналогичное соответствие кривой 3 на рис.10.
То есть можно считать, что
в основном интервале роста константы , то есть при модель квадратичной магнитоупругой связи
описывает наблюдаемый ход периода от величины достаточно
адекватно.
На врезке показана зависимость
периода от константы в более широком диапазоне ее
изменения. Сплошная кривая построена по формуле:
Можно видеть, что отличие
этой формулы от (66) состоит только в небольшом (до 
)
отличии числового коэффициента перед 
, что общего
квадратичного закона не меняет. Наблюдаемое при 
небольшое
(не более 
) превышение измеренной точки над
расчетной кривой, возможно, связано с резонансными свойствами упругой системы.
В любом случае роль
квадратичной зависимости периода от остается решающей.
19. Модель полной зависимости периода медленных колебаний от константы магнитоупругости
На основании
рассмотренного в предыдущих разделах, можно полагать, что наиболее удачной
формулой, описывающей ход зависимости периода от
константы , является следующая:
. (69)
Здесь во-первых учтена роль поперечной составляющей намагниченности по модели эффективных полей и во-вторых – квадратичный характер влияния константы магнитоупругости.
Эта формула является
вполне адекватной в интервале изменения константы магнитоупругости от нудя до , что заведомо перекрывает реальные
значения этой константы для большинства ферритов-гранатов, в том числе для ЖИГ
и ТбФГ.
При больших значениях
константы вплоть до более
удобной является формула (68).
Из аналогии с ходом
зависимости периода простой прецессии намагниченности от константы , показанной на рис.11 (врезка), можно
предположить, что при еще больших значениях константы возрастет
роль продольной составляющей намагниченности, описываемая формулой (57), однако
такое исследование выходит за рамки настоящей работы, так как в настоящее время
лежит далеко за пределами параметров реальных материалов.
Заключение
Основные результаты настоящей работы сводятся к следующему.
Рассмотрена вынужденная нелинейная прецессия вектора намагниченности в нормально намагниченной пластине, обладающей магнитоупругими свойствами. Показано, что в условиях ориентационного перехода, то есть в поле, меньшем размагничивания формы, переменное поле круговой поляризации вызывает прецессию положения равновесия вектора намагниченности, причем за счет магнитоупругости свойства такой прецессии существенно изменяются.
Подробно рассмотрен ориентационный переход вектора намагниченности, состоящий в изменении положения равновесия вектора намагниченности при изменении константы магнитоупругости. На основе минимизации плотности энергии, равной сумме плотностей магнитной, упругой и магнитоупругой энергий, для случая кубической анизотропии с ориентацией типа (100), получена система уравнений относительно компонент намагниченности и упругого смещения, описывающая равновесное положение вектора намагниченности.
С учетом неизменности полной длины вектора намагниченности показана возможность сведения такой системы к одному алгебраическому уравнению третьего порядка. Показано, что в интервале значений константы магнитоупругости, соответствующих реальным материалам, для решения этого уравнения применим метод Кардано, с помощью которого получена аналитическая зависимость продольной и поперечной компонент намагниченности от константы магнитоупругости и других параметров материла и поля.
На основе анализа общего хода зависимости плотности потенциальной энергии от величины константы магнитоупругости, показано, что общее решение упомянутого уравнения имеет три корня, один из которых, соответствующий положительным значениям компонент намагниченности, описывается формулой Кардано, а два других реального физического смысла не имеют.
Выявлена роль магнитоупругого взаимодействии в затягивании поля ориентационного перехода, тем большем, чем магнитоупругая связь выше. Введено понятие поля магнитоупругого взаимодействия, причем показано, что при внешнем поле меньшем этого поля увеличение продольной составляющей намагниченности приводит к уменьшению плотности энергии пластины, а при внешнем поле большем – к ее увеличению.
Показано, что в
равновесном состоянии уменьшение продольной компоненты намагниченности и
соответствующее увеличение поперечной по мере увеличения , сначала довольно быстрое, постепенно
замедляется, после чего останавливается на отклонении вектора намагниченности
от нормали к пластине, равном , при котором обе
нормированные компоненты намагниченности становятся равными 
. При этом в системе наступает не меняющаяся
далее вплоть до спонтанная деформация,
обусловленная взаимным влиянием магнитной и упругой систем.
Найдена постоянная компонента упругого смещения. Показано, что ее связь с константой магнитоупругого взаимодействия описывается линейной зависимостью, прямо пропорциональной произведению продольной и поперечной компонент намагниченности и обратно пропорциональной коэффициенту упругости материала пластины.
На основе связанной системы уравнений движения для намагниченности и упругого смещения проанализированы свойства прецессии второго порядка намагниченности в магнитоупругой среде. Получены параметрические портреты для намагниченности и упругого смещения. Показано, что по мере увеличения магнитоупругой связи диаметр больших колец параметрических портретов увеличивается, причем для компонент намагниченности – сначала линейно с последующим насыщением и выходом на горизонтальный участок, а для компонент упругого смещения – линейно во всем интервале исследованных значений константы магнитоупругости. Ширина больших колец при этом, как для намагниченности, так и для упругого смещения сначала уменьшается, а по мере увеличения магнитоупругой связи стремится к нулю. При этом малые кольца вдоль образующей большого кольца сужения не претерпевают, превращаясь в узкие эллипсы, вытянутые вдоль такой образующей.
Характер изменения геометрических параметров колец параметрических портретов объяснен на основе соответствия радиусов больших колец величинам равновесных значений поперечных компонент намагниченности. Показано, что уменьшение ширины этих колец по мере увеличения константы магнитоупругости определяется сужением потенциальной ямы, дно которой соответствует равновесному значению намагниченности.
Исследована зависимость периода прецессии от величины константы магнитоупругого взаимодействия. Показано, что при малых значениях этой константы период резко уменьшается, тогда как при средних стабилизируется, а при больших – плавно увеличивается тем быстрее, чем значение константы больше.
Для интерпретации наблюдаемого увеличения периода медленных колебаний прецессии намагниченности второго порядка предложено две модели: эффективных полей и квадратичности магнитоупругой связи. Показано, что резкий спад периода при малых значениях константы магнитоупругости можно описать путем введения добавки эффективного поля магнитоупругости, обусловленного поперечной составляющей намагниченности, к поперечной составляющей переменного поля, возбуждающего прецессию.
Для анализа возможности увеличения периода при больших значениях константы рассмотрена простая (первого порядка) свободная прецессия намагниченности в поле, превышающем поле размагничивания формы пластины. Показано, что период такой прецессии прямо пропорционален квадрату константы вплоть до довольно значительных ее значений. При очень больших значениях константы отмечен аномально быстрый рост периода, объяснением которому может явиться возрастание роли эффективного поля, обусловленного продольной составляющей намагниченности.
На основе аналогии с прецессией первого порядка предложена модель квадратичной магнитоупругой связи в качестве причины, вызывающей рост периода прецессии второго порядка при увеличении константы магнитоупругой связи.
В результате совокупного рассмотрения обеих моделей получена аналитическая формула, дающая не только качественное, но и количественное описание зависимости периода прецессии второго порядка от константы магнитоупругой связи с точностью до единиц процентов.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.
2. Ферриты в нелинейных сверхвысокочастотных устройствах. Сб. статей под ред. А.Г. Гуревича. М.: ИЛ. 1961.
3. Моносов Я.А. Нелинейный ферромагнитный резонанс. М.: Наука. 1971.
4. Львов В.С. Нелинейные спиновые волны. М.: Наука. 1987.
5. H. Suhl, Journ. Phys. Chem. Sol. // 1957. V.1. №4. P.209.
6. Temiryazev A.G., Tikhomirova M.P., Zilberman P.E.. // J. Appl. Phys. 1994. V.76. №12. P.5586.
7. Alvarez L.F., Pla O., Chubykalo O. // Phys.Rev.B. 2000. V.61. №17. P.11613.
8. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ, 1995. Т.108. №1. С.281.
9. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.
10. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).
11. Семенцов Д.И., Шутый А.М. // УФН. 2007. Т.177. №8. С.831.
12. Белов К.П., Звездин А.К., Кадомцева А.М., Левитин Р.З. Ориентационные переходы в редкоземельных магнетиках. М.: Наука. 1979.
13. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №1. С.84.
14. Власов В.С., Котов Л.Н., Щеглов В.И. Нелинейная прецессия вектора намагниченности в условиях ориентационного перехода. Сыктывкар: ИПО СыктГУ. 2013.
15. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №9. С.1120.
16. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №6. С.719.
17. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.501.
18. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №8. С.806.
19. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №9. С.857.
20. Вонсовский С.В., Шур Я.С. Ферромагнетизм. М.: ОГИЗ Гостехиздат. 1948.
21. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.
22. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.
23. Comstock R.L., LeCraw R.C. // J. Appl. Phys. 1963. V.34. № 10. P.3022.
24. Ле-Кроу Р., Комсток Р. // В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156.
25. Беляева О.Ю., Зарембо Л.К., Карпачев С.Н. // УФН, 1992, т.162, №2, с.107-138.
26. Голдин Б.А., Котов Л.Н., Зарембо Л.К., Карпачев С.Н. Спин-фононные взаимодействия в кристаллах (ферритах). Л.: Наука. 1991.
27. Сушкевич А.К. Основы высшей алгебры. М.,Л.: Гос. изд. техн.-теор. лит. 1941.
28. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.
29. Туров Е.А., Шавров В.Г. // ФТТ. 1965. Т.7. №1. С.217.
30. Щеглов В.И. // ФТТ. 1972. Т.14. №7. С.2180.
31. Физическая энциклопедия. Т.2. М.: Сов. Энциклопедия. 1990. С.428. Статья “Композиционные материалы”.
32. Власов В.С., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2013. №2. URL: http://jre.cplire.ru/jre/feb13/10/text.html,
http://jre.cplire.ru/jre/feb13/10/text.pdf.
33. Власов В.С., Шавров В.Г., Щеглов В.И. // РЭ. 2014. Т.59. №5. С.482.