"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 11, 2001

оглавление

дискуссия

 

ИСПОЛЬЗОВАНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ ДЛЯ РЕШЕНИЯ ОБРАТНЫХ ЗАДАЧ ЭЛЕКТРОИМПЕДАНСНОЙ И МАГНИТОИНДУКЦИОННОЙ ТОМОГРАФИИ

 

А. В. Корженевский

Институт радиотехники и электроники РАН

 

Получена 27 декабря 2001 г.

 

 

Решение проблемы реконструирования пространственного распределения абсолютной электропроводности ("статической" визуализации) с высоким пространственным разрешением по результатам измерений возмущений квазистационарного электромагнитного поля, проводимых вне исследуемого объекта, открывает широкие перспективы для применения методов электроимпедансной томографии (ЭИТ) и магнитоиндукционной томографии (МИТ) в медицине и других областях. Ни один из существующих методов решения обратной задачи здесь не дает пока удовлетворительных результатов в достижении обеих целей (статической визуализации и удовлетворительного пространственного разрешения) одновременно в случае измерений, проводимых in vivo. Мы исследовали возможность использования искусственных нейронных сетей, обучаемых методом обучения с учителем, для улучшения статической визуализации в низкочастотной электромагнитной томографии. Для ускорения обучения сетей и упрощения оценки степени их адекватности решаемой проблеме, обучающие наборы данных создавались с помощью компьютерного моделирования измерений. В процессе работы тестировались и сравнивались различные алгоритмы оптимизации и структуры нейронных сетей. В результате были получены сети, демонстрирующие высокое качество реконструирования для модельных входных данных с произвольным пространственным распределением электропроводности как для ЭИТ, так и для МИТ. Статические изображения удовлетворительного качества были реконструированы и из экспериментальных данных, измеренных in vivo. В частности, в работе демонстрируется изображение головы добровольца, полученное методом магнитоиндукционной томографии. Показано, что удовлетворительные статические изображения могут быть реконструированы даже с использованием однослойных линейных искусственных нейронных сетей.

 

1.      Введение

 

Низкочастотная электромагнитная томография это интроскопический метод, с помощью которого может быть реконструировано распределение электрического импеданса внутри объекта, такого как тело человека, по результатам измерений квазистационарного ("мягкого") электрического или магнитного поля, возмущенного объектом. Задача реконструирования изображений в низкочастотной электромагнитной томографии, такой как электроимпедансная томография (ЭИТ) или магнитоиндукционная томография (МИТ), является примером нелинейной некорректной обратной задачи [1-3]. Осуществление статической ("безопорной") визуализации и достижение высокого пространственного разрешения является ключевой проблемой для внедрения таких методов в клиническую практику. Ни один из существующих алгоритмов не дает удовлетворительных результатов в решении обеих проблем одновременно в случае использования данных, измеренных in vivo (на реальном человеческом теле). Мы исследовали возможность использования искусственных нейронных сетей, обучаемых методом обучения с учителем, для повышения качества статической визуализации в такой томографии "мягким полем". Первые успешные результаты использования искусственных нейронных сетей для реконструирования изображений в ЭИТ были опубликованы в [4], где т.н. Адаптивные Линейные Элементы (линейные нейронные сети) были использованы для динамической визуализации (визуализации изменений) электропроводности как для симулированных, так и для экспериментальных входных данных. Мы попытались расширить применение нейронных сетей и использовать их для статической визуализации в электроимпедансной  и магнитоиндукционной томографии.

Искусственная нейронная сеть представляет собой совокупность относительно простых однотипных вычислительных узлов (нейронов), связанных друг с другом многочисленными настраиваемыми связями [5]. Работа нейронной сети сводится к формированию некоторого полезного выходного набора данных в ответ на совокупность входных данных, т.е. реализации некоторого функционального преобразования данных. Свойства сети определяются не столько свойствами нейронов, сколько структурой и свойствами связей между ними.

Процесс настройки связей с целью придания сети необходимых свойств называется обучением нейронной сети. Наиболее распространенный метод обучения – обучение с учителем предполагает наличие набора пар входных и соответствующих им желаемых выходных данных, называемого обучающей выборкой. Используя невязку реального и желаемого ответа сети для всех примеров обучающей выборки, оптимизируют связи сети, минимизируя эту невязку. Для того, чтобы сделать решение устойчивым к возможным шумам и ошибкам в измеренных данных, к входным данным обучающей выборки в процессе обучения добавляется шумовая компонента.

В многослойных нейронных сетях нейроны организованы в слои, так что связанными между собой являются только нейроны из смежных слоев. Согласно теореме об аппроксимации для двухслойной сети, первый слой которой состоит из нейронов с нелинейной сигмоидальной передаточной функцией, а второй – из линейных сумматоров, для любой непрерывной функции произвольного конечного числа аргументов существует конечная нейронная сеть, аппроксимирующая эту функцию с любой наперед заданной точностью. Таким образом, если обратная задача, такая как задача электроимпедансной или магнитоиндукционной томографии, имеет решение (с необходимой степенью регуляризации некорректной задачи), она может быть решена с помощью искусственной нейронной сети.

Нейронная сеть может состоять и из единственного слоя линейных элементов. Такая сеть может аппроксимировать только линейные зависимости, однако часто простота создания и обучения таких сетей в совокупности с их малой чувствительностью к ошибкам масштабирования входных данных делает оправданным их применение и для решения нелинейных задач, таких как обратные задачи электромагнитной томографии. В наших экспериментах мы использовали оба типа сетей.

           

2.      Методы

 

Для создания обучающих наборов данных для нейронных сетей, выполняющих реконструирование изображений, использовалось численное моделирование процесса измерения. Исходные распределения электропроводности в рабочей области томографа генерировались с помощью генератора случайных чисел с последующей пространственной фильтрацией фильтром низких частот (использовался Гауссовский фильтр) с целью уменьшения вклада высокочастотных (мелкомасштабных) компонент. Обучающие наборы данных состояли из 1 – 2 тысяч примеров. Для придания нейронной сети регуляризирующих свойств и способности реконструировать изображения, используя данные неидеальных измерительных систем, к входным данным в процессе обучения добавлялся шумовой сигнал, величина которого варьировалась в интервале 0,5 - 5% от максимальной величины входного сигнала в выборке. Такой шум может моделировать как реальную шумовую компоненту во входных данных, так и такие непредсказуемые факторы как неточность расположения электродов на теле пациента и геометрия самого тела.

Эксперименты проводились с двумя типами искусственных нейронных сетей: нелинейной двухслойной сетью с сигмоидальной передаточной функцией нейронов скрытого слоя и линейными сумматорами в выходном слое, а также с набором независимых линейных сетей, каждая из которых имела один выход, соответствующий яркости одного пикселя реконструируемого изображения.

Количество нейронов в скрытом слое двухслойной сети определяет способность сети аппроксимировать требуемое преобразование. Выбор этого количества определяется в значительной степени опытом и интуицией. Недостаточное количество нейронов делает выполнение требуемой аппроксимации сетью невозможным, а избыточное количество уменьшает генерализирующую (обобщающую) способность сети. После нескольких проб конфигурация сети с 60 нейронами в скрытом слое была признана подходящей для решения обратных задач ЭИТ с шестнадцатью электродами и МИТ с шестнадцатью индукторами и детекторами. Работа такой сети описывается выражением:

 

,

 

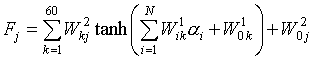где  - яркость j-го пикселя реконструируемого изображения,  и  - весовые матрицы входов первого и второго слоев сети,  - входные данные (результаты измерений), N – количество входных величин. Структура сети показана на рис. 1. Обучение сети проводилось методом обратного распространения ошибки. При этом оптимизация методом сопряженных градиентов показала наилучшие результаты (скорость и качество обучения).

 

 

 

Рис. 1. Структура двухслойной искусственной нейронной сети используемой для ЭИТ и МИТ визуализации: (1) - вход (192 разности потенциалов для 16-электродной ЭИТ системы с полярной инжекцией тока или 240 сдвигов фаз для 16-катушечной МИТ системы); (2) - скрытый слой (60 нейронов с сигмоидальной функцией возбуждения); (3) - выходной слой (линейные сумматоры), представляющий 164 пикселя изображения.

 

Структура линейной сети полностью определяется количеством ее входов и выходов. Линейная сеть может быть создана и "обучена" за один шаг с использованием метода наименьших квадратов. Такие сети весьма полезны для оценки полноты обучающей выборки. Кроме того линейность сети делает ее менее чувствительной к неточностям масштабирования данных, что весьма полезно, когда сеть, обученная по результатам двумерного моделирования, используется для реконструирования изображений по экспериментальным данным. Для решения задачи визуализации создавался набор линейных сетей, имеющих количество входов равное размеру вектора входных данных и один выход, соответствующий яркости одного пикселя реконструируемого изображения. Количество таких сетей равнялось количеству пикселей в реконструируемом изображении - 164 пикселя внутри реконструируемой круговой области в наших экспериментах. Их функционирование описывается выражением:

 

.

 

Проблема реконструирования ЭИТ изображений была рассмотрена для случая шестнадцатиэлектродной измерительной системы с полярной инжекцией тока. Прямая задача сводится к решению уравнения Лапласа для неоднородной среды. Экспериментальные данные были получены с помощью измерительной системы, описанной в [6]. Обучающий набор данных генерировался с помощью двумерной модели конечных элементов для уравнения Лапласа в предположении цилиндрической геометрии исследуемого объекта. Качество визуализации с помощью нейронных сетей сравнивалось с результатами реконструирования методом обратной проекции вдоль эквипотенциалей электрического поля с синтезом опорного набора данных [6, 7]. Архитектура нейронных сетей определяется количеством входных сигналов (192 для 16-электродной ЭИТ с полярной инжекцией тока), количеством выходных пикселей (164) и количеством нейронов в скрытом слое (60).

В магнитоиндукционной томографии измерения возмущений переменного магнитного поля, вызванных вихревыми токами, используется для определения распределения электропроводности внутри объекта [2, 3]. В экспериментальной измерительной системе [8] используется 16 индукторов и 16 детекторов магнитного поля, окружающих рабочую область томографа. В качестве исходных данных для реконструкции изображений используются измеренные сдвиги фаз между напряжением, приложенным к индуктору и напряжением, измеряемым каждым из детекторов. В настоящее время в качестве основного алгоритма визуализации используется метод свертки и обратной проекции вдоль линий индукции невозмущенного магнитного поля. Этот линейный метод позволяет реализовать только динамическую визуализацию, т. е. визуализацию изменений распределения электропроводности, произошедших между двумя последовательными измерениями. Использование искусственной нейронной сети могло бы решить проблему статической визуализации в МИТ. Архитектура линейной и нелинейной сетей, использованных для реконструирования изображений в МИТ, такая же как и сетей, использованных для случая ЕИТ, за исключением количества входных сигналов, которое равно 240 для 16-катушечной измерительной системы. При создании обучающих наборов данных мы исходили из предположения о малом возмущении магнитного поля индуктора исследуемой средой. Индуктор аппроксимировался точечным магнитным диполем. Возмущение магнитного поля индуктора проводящей средой может быть приближенно вычислено с помощью следующего выражения:

 

,

 

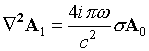где  и  - векторный потенциал невозмущенного магнитного поля и его возмущения, вызванного проводящей средой с проводимостью . Взяв в качестве  векторный потенциал магнитного диполя, для амплитуды возмущения индукции магнитного поля  получим:

 

,

 

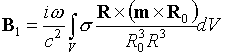где m – амплитуда магнитного момента индуктора,  - радиус-вектор из индуктора в точку интегрирования (),  - радиус-вектор из  в точку наблюдения. Это уравнение справедливо при весьма жестких ограничениях: слабое влияние среды на магнитное поле, пренебрежимый вклад токов смещения по сравнению с токами проводимости, слабое влияние потенциального электрического поля на распределение токов (в частности, отсутствие изоляционных барьеров внутри среды). Тем не менее такие ограничения представляются вполне оправданными во многих случаях при визуализации биологических объектов. Для создания обучающих наборов данных, как и в случае ЭИТ, использовались фильтрованные случайные распределения электропроводности. Соответствующие измеряемые сдвиги фаз вычислялись затем для этих распределений с помощью описанного выше подхода.

3. Результаты

 

3.1. Электроимпедансная томография

 

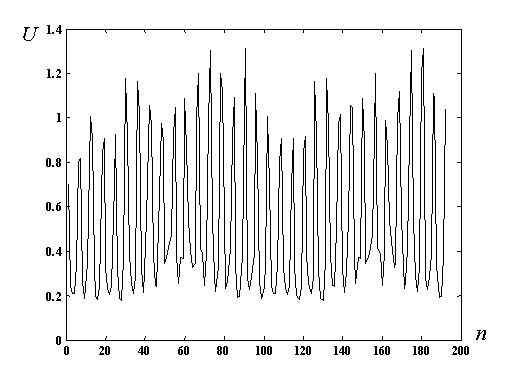
Результаты статической визуализации тестовых распределений электропроводности, осуществляемой обученной двухслойной нейронной сетью по данным, вычисленным с помощью двумерной модели конечных элементов, весьма обнадеживающе – см. рис. 2. Увеличение уровня шума во входных данных до разумных пределов приводит лишь к уменьшению разрешающей способности, преимущественно в центре изображения. Попытки реконструировать изображения из экспериментально измеренных данных не привели, однако, к удовлетворительным результатам, хотя метод обратного проецирования с синтезом опорных данных, который используется в настоящее время в томографической системе, дает вполне удовлетворительные изображения для тех же данных – рис. 3. Вероятной причиной такого отличия является различие пространственных зависимостей полей в случае двух и трех измерений. Это различие делает некорректным использование сети, обученной с использованием двумерного моделирования, для работы с экспериментальными данными, соответствующими реальному трехмерному миру. В частности, если отношение максимальной измеренной разности потенциалов к минимальной в трехмерном случае составляет примерно 1 к 0.2 – см. экспериментальную кривую на рис. 4а, то в двумерном случае это отношение составляет примерно 1 к 0.6 – см. результат моделирования на рис. 4б.

 

 

 

 

Рис 2. Результаты статической ЭИТ визуализации случайных распределений электропроводности с помощью двухслойной нейронной сети. В качестве входных данных использованы результаты двумерного моделирования с добавлением шумовой компоненты.

 

 

 

 

 

Рис. 3. Статическое ЭИТ изображение грудной клетки добровольца реконструированное методом обратной проекции с синтезом опорных данных. Светлые тона соответствуют высокой электропроводности.

 

 

(а)

 

(б)

 

Рис. 4. Входные данные для ЭИТ реконструкции полученные путем измерений на грудной клетке добровольца (а) и вычисленные с помощью двумерной модели, основанной на методе конечных элементов, с использованием аналогичного пространственного распределения электропроводности (б). U - нормированные разности потенциалов между соседними электродами, n - номер измерения согласно используемой стратегии измерений.

 

Набор линейных нейронных сетей, обученных по результатам такого же двумерного моделирования, дает вполне удовлетворительные результаты визуализации по тем же экспериментальным данным. Результат такой визуализации показан на рис. 5. Изображение выглядит деформированным - стянутым к центру и неадекватным на периферии, однако все анатомические структуры, видимые на рис. 3, имеются и на изображении, реконструированном нейронной сетью. Конечно, линейность нейронной сети ограничивает ее способность решать нелинейную обратную задачу, каковой является задача ЭИТ. Однако малая чувствительность такой сети к масштабу вариации входных данных оказалась жизненно важной в случае реконструирования изображений по трехмерным входным данным сетью, обученной с помощью двумерной модели измерительной системы.

 

 

Рис. 5. Статическое ЭИТ изображение грудной клетки добровольца реконструированное линейной нейронной сетью, обученной с помощью двумерной конечноэлементной модели. Использованы те же входные данные, что и для рис. 3.

 

 

3.2. Магнитоиндукционная томография

 

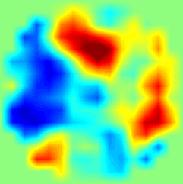
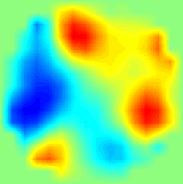
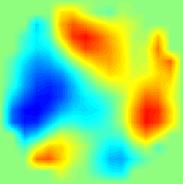
Результаты визуализации с помощью двухслойной нелинейной сети для модельных входных данных показаны на рис. 6, где несколько случайных распределений электропроводности представлены в левой колонке, а соответствующие реконструированные изображения при различном уровне шума, добавленного к входным данным, показаны справа. Сеть демонстрирует возможность великолепной статической визуализации. Увеличение зашумленности входных данных приводит к уменьшению разрешающей способности преимущественно в центре изображения.

 

 

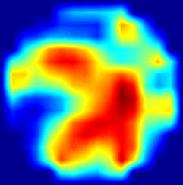
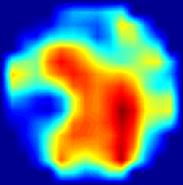
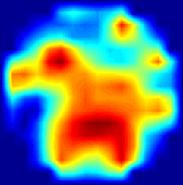
Рис. 6. Результаты статической МИТ реконструкции случайных распределений электропроводности при различных уровнях входного шума с помощью двухслойной нейронной сети.

 

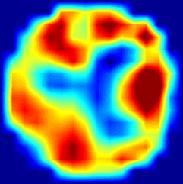
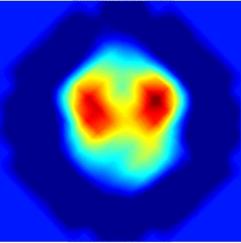
Статическая визуализация распределения электропроводности внутри протяженных объектов потребовала большей точности измерений, чем использовавшаяся ранее динамическая визуализация методом свертки и обратной проекции. Первые эксперименты по in vivo МИТ статической визуализации оказались не очень успешными из-за несовершенства измерительной системы. После дополнительного экранирования индукторов, заметно уменьшившего влияния емкостной связи между индукторами и детекторами, были получены первые стабильные и воспроизводимые статические МИТ изображения по результатам измерений, проведенных in vivo. Изображения были реконструированы с помощью искусственной нейронной сети. В частности, такое изображение головы добровольца приведено на рис. 7. Два ярких пятна в центральной области изображения соответствуют регионам с высокой электропроводностью и могут быть идентифицированы как желудочки мозга, заполненные спинномозговой жидкостью. Электропроводность спинномозговой жидкости в 5 – 10 раз превосходит электропроводность других тканей мозга [9] на рабочей частоте измерительной системы (20 МГц). Это обуславливает высокий контраст изображения.

 

 

Рис. 7. Статическое МИТ изображение головы добровольца, реконструированное с помощью линейной нейронной сети. Затылок находится в верхней части изображения, правая сторона - в левой части изображения. Два красных пятна, соответствующих областям высокой электропроводности, могут быть идентифицированы как желудочки мозга.

 

4. Выводы

 

Искусственные нейронные сети могут быть использованы для решения обратных задач электроимпедансной и магнитоиндукционной томографии. В частности, тесты с модельными и экспериментальными данными демонстрируют принципиальную возможность статической визуализации удовлетворительного качества с невысокими вычислительными затратами. Статическая визуализация in vivo реализована с помощью искусственных нейронных сетей как в ЕИТ, так и в МИТ. Преимущества описанных методов включают возможность весьма тонкой регуляризации решения обратной задачи, которая может принимать во внимание такие факторы, как неопределенность геометрии обследуемого тела. Для этого в обучающий набор данных должны быть включены примеры с искаженной случайным образом формой границы тела.

Основной проблемой на пути практического применения искусственных нейронных сетей для визуализации в низкочастотной электромагнитной томографии является необходимость синтеза обширных высококачественных обучающих наборов данных. Для решения этой проблемы необходима разработка реалистичных трехмерных моделей, основанных на методе конечных элементов, для решения соответствующих прямых задач.

Упрощенные и двумерные модели для решения прямой задачи могут быть использованы в сочетании с линейными нейронными сетями, менее чувствительными к некорректным зависимостям во входных данных, чем многослойные нелинейные сети. Представленные результаты демонстрируют хорошие характеристики таких линейных сетей даже при решении таких реально нелинейных задач, как задачи томографии "мягким полем".

 

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 01-01-00982.

Список литературы

[1] Barber D. C. and Brown B. H. Applied potential tomography // J. Phys. E: Sci. Instrum., 1984, v 17, p. 723-733

[2] Корженевский А.В., Черепенин В.А. Магнито-индукционная томография // РЭ, 1997, т. 42, N 4, с. 506-512

[3] Корженевский А.В., Черепенин В.А. Магнитоиндукционная томография // Журнал Радиоэлектроники, 1998, № 1, http://jre.cplire.ru/win/dec98/1/text.html

[4] Adler A. and Guardo R. A neural network image reconstruction technique for electrical impedance tomography // IEEE Trans. Med. Imag., 1994, v. 13, p. 594-600

[5] Caudill M. Neural Networks Primer, San Francisco CA: Miller Freeman Publications, 1989

[6] Корженевский А.В., Корниенко В.Н., Культиасов М.Ю., Культиасов Ю.С., Черепенин В.А. Электроимпедансный томограф для медицинских приложений // ПТЭ, 1997, N 3, с. 133-140

[7] Korjenevsky A.V. Reconstruction of absolute conductivity distribution in electrical impedance tomography // Proc. 9th Int. Conf. On Electrical Bio-Impedance (Heidelberg, 1995), p. 532-535

[8] Korjenevsky A., Cherepenin V. and Sapetsky S. Magnetic induction tomography: experimental realization // Physiol. Meas., 2000, v. 21, p. 89-94

[9] Gabriel C. and Gabriel S. Compilation of the dielectric properties of body tissues at RF and microwave frequencies, Physics Department King's College London Report AL/OE-TR-1996-0037, http://niremf.iroe.fi.cnr.it/docs/DIELECTRIC/Report.html