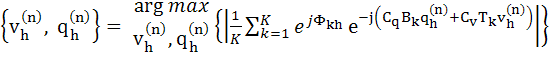Исследование зависимости результатов обработки радиолокационных данных ДЗЗ от параметров обработки. Часть 1. Ключевые моменты метода постоянных рассеивателей.

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ РЕЗУЛЬТАТОВ ОБРАБОТКИ РАДИОЛОКАЦИОННЫХ ДАННЫХ ДЗЗ ОТ ПАРАМЕТРОВ ОБРАБОТКИ

ЧАСТЬ 1. КЛЮЧЕВЫЕ МОМЕНТЫ МЕТОДА ПОСТОЯННЫХ РАССЕИВАТЕЛЕЙ

А. А. Феоктистов ¹, А. И. Захаров ², М. А. Гусев ¹, П. В. Денисов ¹

¹ Научный центр оперативного мониторинга Земли ОАО “Российские космические системы”

² Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН

Статья получена 5 декабря 2014 г.

Аннотация. Представлено детальное описание ключевых моментов двух наиболее известных вариантов метода постоянных рассеивателей. Отмечены основные особенности метода, реализованного в модуле постоянных рассеивателей (persistent scatterers, PS) программного пакета SARscape.

Ключевые слова: метод постоянных рассеивателей, РСА, ASAR/ENVISAT, SARscape, атмосферный фазовый экран, ЦММ.

Abstract: Detailed description of two popular versions of persistent scatterers technique is presented. Basic features of PS algorithm implementation in the SARscape package are described.

Key words: persistent scatterers technique, PS, SAR, ASAR/ENVISAT, SARscape, atmospheric phase screen, APS, DEM.

1. Введение

Научный центр оперативного мониторинга Земли (НЦ ОМЗ) ОАО «Российские космические системы» проводит исследование и отработку технологий интерферометрической [1-2] и дифференциальной интерферометрической [3-4] обработки радиолокационной информации. Цель проведения данных работ – создание опережающего задела в области концептуально-методологических основ разработки программно-аппаратных средств обработки данных перспективных отечественных космических комплексов радиолокационного наблюдения. Отработка проводится с использованием коммерческого программного обеспечения, в частности, одного из самых распространенных в России программных пакетов SARscape (фирма Sarmap s.a., Швейцария) и данных современных зарубежных РСА космического базирования.

На практике возможности классических методов интерферометрической и дифференциальной интерферометрической обработки данных РСА при измерении рельефа и подвижек отражающей поверхности существенно ограничены эффектами пространственной и временной декорреляции сигналов РСА в сеансах съемки интерферометрических пар изображений, а также флуктуациями фазы сигналов на атмосферных неоднородностях [5]. Интенсивно развиваемые современные методы дифференциальной интерферометрической обработки – метод постоянных рассеивателей (PS) и метод малых базовых линий (SBAS) – основаны на совместном использовании временных серий изображений, получаемых в интерферометрическом режиме съемки. Использование упомянутых методов позволяет резко ослабить влияние искажающих факторов и довести точность создаваемых цифровых моделей местности (ЦММ) до долей метра, цифровых карт смещений (ЦКС) – до долей миллиметра [6-8].

В данной работе представлены результаты исследования возможностей метода PS на примере программного пакета SARscape 5.0 и тестового набора данных РСА ASAR/ENVISAT.

Необходимо отметить, что в пакете SARscape отсутствует подробная программная документация по методу PS, а оперативная программная документация (в виде HELP) – неполная, с противоречиями. Вместо описания реализованного алгоритма приведена ссылка на три уже ставшие «классическими» первоисточника [6-8], в которых описаны совершенно разные варианты алгоритма и которые содержат ряд неточностей и ошибок. Реализованный в модуле PS алгоритм содержит целый ряд принципиально новых моментов и существенно отличается от любого из трех описанных в [6-8] прототипов. В посвященных данной теме немногочисленных работах российских авторов, например [11-12], отсутствует описание большинства критически важных физических аспектов проблемы.

Содержащийся в работе обзор ключевых моментов метода PS устраняет данный пробел в отечественной литературе – в целях обеспечения эффективного развития технологий радиолокационного наблюдения и целевого применения средств. При этом элементарные сведения об основах классической радарной интерферометрии не приведены, они могут быть найдены, например, в [5].

2. Ключевые моменты метода PS

Основное отличие метода PS от классической радарной интерферометрии заключается в том, что он предназначен для работы в условиях крайне низкой когерентности отраженных сигналов, из-за чего подавляющая часть элементов изображения (пикселей) оказывается неинформативной. Задачи выявления подвижек подстилающей поверхности и измерений рельефа решают с помощью этого метода для ограниченного набора так называемых постоянных рассеивателей, выделяемых по специальной методике, суть которой будет изложена далее. Этот полуэмпирический метод позволяет решать указанные выше задачи в условиях влияния атмосферных неоднородностей и высокой степени пространственной и временной декорреляции.

2.1. Метод, основанный на линеаризации атмосферных параметров

Метод разработан для анализа постоянных рассеивателей, наблюдаемых в большом количестве на территориях типа городской застройки. По существу, постоянные рассеиватели – это точечные объекты типа “квазиуголковых” отражателей, которые обеспечивают достаточно сильный и устойчивый во времени отраженный сигнал [7].

2.1.1. Совмещение изображений и расчет интерферограмм. Метод основан на одновременном использовании временных серий изображений, полученных в повторяющейся геометрии съемки. Во временной серии выбирается опорное изображение. Каждое из K оставшихся изображений совмещается с субпиксельной точностью с опорным и формируется набор из K интерферограмм.

При проведении расчета интерферограмм одновременно выполняется процедура выравнивания, в рамках которой осуществляется компенсация топографической компоненты фазы, связанной с высотой [5]. Значения высоты берутся из опорной ЦММ, в качестве которой обычно используется SRTM с пространственным разрешением 90 м и абсолютной точностью значений высот около 16 м [13]. Чтобы избежать «слипания» часто идущих интерференционных полос в случае больших базовых линий формируется повторная выборка, полученная в результате избыточной дискретизации [9].

2.1.2. Формирование стартового набора кандидатов в постоянные рассеиватели. Стартовый набор из H кандидатов в постоянные рассеиватели (PSС) формируется с использованием индекса дисперсии амплитуды значения которого рассчитываются для всех пикселей изображения [6-7]:

, (1)

где m_A– среднее по K+1 изображениям серии значение амплитуды рассматриваемого пикселя, а σ_A – среднеквадратичное отклонение.

Считается, что при выполнении условия:

, (2)

рассматриваемый пиксель обладает достаточно стабильными характеристиками сигнала (амплитуда, фаза) и может быть включен в стартовый набор PSC [6-7].

2.1.3. Устранение фазового пьедестала на интерферограммах. Фазовый пьедестал (аддитивная константа), который по определению имеется у каждой интерферограммы [5], устраняется с помощью PSC_min, имеющего минимальное значение индекса рассеяния амплитуды. Из фазы каждого пикселя вычитается одна и та же постоянная величина PSC_min, разная у разных интерферограмм. В результате фаза пикселя PSC_min должна оказаться равной нулю на всех интерферограммах.

2.1.4. Матричная система уравнений. Метод PS содержит два принципиально важных предположения. Во-первых, предполагается, что для относительно небольших фрагментов изображений размером на поверхности Земли до 5 x 5 км² атмосферные искажения в виде флуктуаций фазы сигнала на неоднородностях (атмосферные фазовые экраны, Atmospheric Phase Screen, APS) медленно изменяются в пространстве и могут описываться линейной функцией, содержащей среднее значение и два коэффициента, характеризующие линейный ход атмосферных флуктуаций фазы по дальности и по азимуту. Во-вторых, предполагается линейная зависимость величин смещений PSС от времени [7].

С учетом сделанных предположений формируется матричная система уравнений:

, (3)

где точкой обозначено матричное умножение векторов.

В левой части уравнения (3) – матрица размера [K x H]; K – число изображений (т.е. строк); H – число найденных PSC (т.е. столбцов):

. (4)

Произвольный элемент матрицы – значение фазы для PSC с номером h (h=1,…,H), взятое из интерферограммы с номером k (k=1,…,K).

Все 6 членов в правой части уравнения (3) – матрицы того же размера [K x H]. Первые 5 членов справа в сумме дают рассчитываемую аппроксимацию для матрицы . Последний член – матрица – это матрица невязки, или фазовых остатков, равная поэлементной разности матрицы истинных значений фазы (слева) и их аппроксимации (справа).

Первые 5 членов в правой части формируются в результате матричного произведения векторов. Левые сомножители – 5 вертикальных вектор-столбцов; все они имеют размеры [K x 1]:

, (5)

где – неизвестная постоянная атмосферная компонента для изображения k; и – неизвестные коэффициенты у линейных атмосферных компонент для направлений по азимуту и наклонной дальности для изображения k; – известная нормальная компонента базовой линии для изображения k; – известный временной интервал между съемками k-ого и опорного изображений.

Правые сомножители – горизонтальные (транспонированные, символ T) вектор-строки; все они имеют размер [1 x H]:

(6)

где – вспомогательный единичный вектор-строка; и – известные координаты в направлении по азимуту и наклонной дальности для PSC с номером h; – неизвестное значение остаточной высоты для PSC с номером h, умноженное на коэффициент:

, (7)

– неизвестное значение скорости для PSC с номером h, умноженное на коэффициент:

(8)

Замечание. Необходимо уточнить: остаточная высота – это корректирующая поправка, которая рассчитывается в рамках метода PS и которая позволяет уточнить исходное значение высоты из опорной ЦММ SRTM. Вклад фазовых компонент, связанных с исходными значениями высоты PS из опорной ЦММ (топографической фазы), в значения фазы в левой части уравнения (3) скомпенсирован на этапе совмещения изображений и расчета интерферограмм, вследствие чего соответствующие члены отсутствуют и в правой части этого уравнения.

В качестве примера ниже приведен результат матричного умножения двух векторов с формированием второй матрицы справа в уравнении (3):

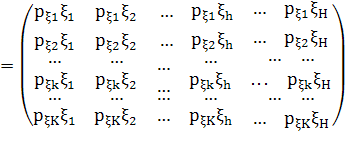. (9)

Обратим еще раз внимание на матричное уравнение (3), знак равенства в котором определяет, что должно быть выполнено равенство для каждого элемента k, h. Таким образом, матричное уравнение (3) эквивалентно совокупности [H x K] "поэлементных" уравнений следующего вида:

. (10)

2.1.5. О точности расчетов значений скорости смещений и остаточных высот. Точность получаемых оценок для скорости смещения и остаточной высоты постоянных рассеивателей зависит от распределения значений нормальных компонент базовой линии и временных интервалов между съемками опорного и парного изображений. При высоких отношениях сигнал/шум имеют место следующие выражения для дисперсии оценок остаточной высоты и скорости смещений [7]:

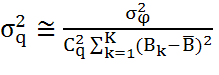, (11)

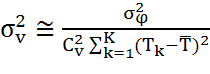, (12)

где: – дисперсия фазового шума PS, определяемая пороговым значением когерентности по ансамблю изображений (21); и – значения нормальных компонент базовой линии и временных интервалов между съемками опорного и парного изображения k, соответственно; и – средние по набору изображений значения нормальных компонент базовой линии и временных интервалов.

2.1.6. Решение системы уравнений с использованием методики простой периодограммы. Количество неизвестных, которые предстоит определить, равно 3K + 2H; это векторы (первые три вектора имеют размер K, последние два – H).

Данные содержатся в матрице и в четырех векторах . Объем данных в матрице равен [K x H], в векторах 2H + 2K (первые два вектора имеют размер H, последние два – K). Задача состоит в том, чтобы найти такие значения неизвестных, которые минимизируют совокупность [K x H] элементов матрицы фазовых остатков .

Если бы в системе уравнений (3) использовались развернутые значения фазы, система была бы линейной и было бы естественно искать ее решение в матричном виде. Однако, система уравнений является нелинейной, поскольку фазы интерферограмм свернуты по модулю 2π [5-7].

Ввиду нелинейности матричной системы уравнений в [7] предложено реализовать ее решение на основе итерационного алгоритма, в рамках которого на каждой итерации n вычислительного процесса:

• сначала для каждого PSC с номером h (h=1,…,H) проводится оценка значений его скорости смещений и остаточной высоты ,

• с использованием полученного массива данных и проводится оценка значений трех атмосферных параметров , и для каждой интерферограммы k.

Оценка значений скорости смещений и остаточной высоты для каждого PSC с номером h проводится с использованием так называемой методики простой периодограммы [7]:

(13)

в рамках которой должны быть найдены такие значения и , при которых достигается максимальное значение для выражения, стоящего в правой части уравнения (13). Отметим, что именно использование конструкции, основанной на экспоненте, “нечувствительной” к фазовым компонентам, кратным 2π, и позволяет использовать свернутые значения фаз интерферограмм.

С использованием полученного массива данных и последующая оценка значений трех атмосферных параметров ,и для каждого изображения k проводится также в рамках методики простой периодограммы [7]:

(14)

При этом в величинахв (14) предварительно должны быть скомпенсированы рассчитанные в (13) фазовые компоненты:

, (15)

связанные со скоростью смещений и остаточной высотой PSC.

Необходимо пояснить, что параметры и вуравнении (14)определяются точно так же, как это делалось при решении уравнения (13), а параметр соответствует значению фазы в (14) при Вычисления в рамках итерационного алгоритма прекращаются после выполнения условий порогового типа, сформулированных в критерии сходимости. В итоге на выходе формируются:

• значения трех атмосферных коэффициентов , и для атмосферного экрана каждой интерферограммы k (k=1,…,K);

• H значений средней скорости и остаточной высоты – для каждого PSC_h (h=1,…,H).

2.1.7. Устранение атмосферных искажений. Используя найденные атмосферные коэффициенты , и , рассчитываются фазовые поправки, или атмосферные фазовые экраны, для всех пикселей каждой интерферограммы k:

, (16)

Однако, прежде чем использовать рассчитанные атмосферные фазовые экраны для устранения атмосферных искажений, проводится их высокочастотная фильтрация по оси времени. Сначала рассчитывается скорректированное значение атмосферной фазы для опорного изображения. Использование этой процедуры позволяет сформировать более корректные временные тренды смещений постоянных рассеивателей [6-9].

Существуют два варианта расчета :

1) Первый вариант реализуется путем усреднения атмосферных фазовых экранов по всему набору интерферограмм с дальнейшим расчётом уточненного атмосферного экрана для каждой интерферограммы k [6]:

, (17)

, (18)

2) Второй вариант отличается от первого тем, что при формировании атмосферной фазы для опорного изображения в формулу суммирования вводятся весовые коэффициенты, с помощью которых реализуется процедура усреднения с использованием так называемого треугольного фильтра по оси времени [7, 9], имеющего следующий вид:

, (19)

где – модуль временного интервала между съемками изображения k и опорного в днях; – полуширина фильтра по времени в днях; – нормировочная константа.

В результате при формировании атмосферной фазы для опорного изображения

, (20)

весовые коэффициенты максимальны для парных изображений, близких по времени к моменту съемки опорного изображения, и уменьшаются по линейному закону до нуля при приближении значений к _.

2.1.8. Поиск расширенного набора PS. Процедура поиска расширенного набора PS по всему набору пикселей основана на использовании порогового значения когерентности по ансамблю интерферограмм (пороговое значение равно 0,75 [7]):

, (21)

где в показателе экспоненты содержатся значения остаточной фазы , возникающей после удаления фазовых компонент, обусловленных подвижками и ошибками по высоте и рассчитываемых с помощью методики простой периодограммы (13). Отличие от (13) состоит только в том, что в данном случае в значениях фазы уже устранены атмосферные искажения. Суммирование выполняется по всем интерферограммам.

2.1.9. Условия существования решения и обеспечения быстрой сходимости. В работе [7] отмечается, что нелинейная система уравнений (3) может быть решена при условии, что:

· отношение сигнал/шум для отобранных PS достаточно велико;

· справедливо предположение о линейноcти скорости смещения PS;

· справедливо предположение о локальной линейности флуктуаций свойств атмосферных неоднородностей в пространстве.

Отмечается также, что для обеспечения достаточно быстрой сходимости необходимы:

· однородность двумерного распределения параметров съемки в координатах нормальной компоненты базовой линии и интервалов времени между съемками опорного и парных изображений (не должно быть значительных пропусков);

· точность значений высот в опорной ЦММ порядка 20 м и лучше;

· значения скорости смещений PS на уровне единиц – десятков мм/год.

2.2. Метод, основанный на развертке атмосферной фазы

В рамках этого метода для каждого PSC также оцениваются значения скорости смещений и высоты (13). Но вместо последующей оценки всей совокупности неизвестных линейных атмосферных параметров , и (14), используется другой подход. Фазовые остатки w_k, остающиеся в показателях экспонент в правой части уравнения (13) для каждой интерферограммы с номером k (после удаления фазовых компонент, связанных со смещением и высотой PSC), интерпретируются как атмосферная фаза. Шумовые компоненты сигнала подавляются за счет низкочастотной пространственной фильтрации.

В данном методе реализована одна из стандартных процедур развертки значений атмосферной фазы для узлов нерегулярной сетки, соответствующих значениям координат найденных PSC [6]. Развертка выполняется только для тех пар PSC, относительное расстояние которых не превышает одного километра и значение попарной когерентности PSC по ансамблю изображений (22) превышает пороговое значение:

, (22)

где – разность рассчитанных значений атмосферной фазы для рассматриваемой пары PSC (по интерферограмме k). С целью повышения точности оценки атмосферных фазовых экранов рассчитанные значения попарной когерентности PSC используются в алгоритмах развертки фазы в качестве весовых коэффициентов [6].

Дополнительно, с целью подавления шума, проводится низкочастотная пространственная фильтрация с использованием процедуры усреднения в пределах квадратного окна с линейными размерами L=2000 м. Затем выполняется высокочастотная фильтрация по времени (19)-(20).

В [6] показано, что для успешного завершения работы алгоритма, основанного на развертке атмосферной фазы, достаточна плотность PSC порядка нескольких единиц на км².

Метод позволяет провести начальную оценку и устранение атмосферных искажений, после чего может быть запущена итерационная процедура, в рамках которой последовательно уточняются и значения скорости смещений и высоты для расширенного набора PS. Их поиск проводится по полному набору пикселей с использованием в качестве критерия отбора порогового значения для когерентности по ансамблю изображений (21).

Замечание. В случае необходимости, после формирования расширенного набора PSC может быть запущен алгоритм, основанный на линеаризации атмосферных параметров (раздел 2.1). Для его успешного запуска необходимо использование более высокой "стартовой" плотности PSC [7].

3. Особенности метода, реализованного в модуле PS пакета SARscape 5.0

Реализованный в модуле PS метод близок к методу, описанному в разделе 2.2, но имеет ряд особенностей [9, 10].

При проведении обработки не выполняется развертка фазы, чтобы исключить возникающие при выполнении данной процедуры ошибки [10]. Вследствие этого, при выполнении низкочастотной пространственной фильтрации с целью сохранения резких границ в области скачков неразвернутой фазы (от –π до +π), совершенно очевидно, возникает необходимость использования фильтра медианного типа вместо усреднения в пределах квадратного окна. По умолчанию в модуле PS линейные размеры L для фильтра данного типа принимаются равными L=1200 м и, в случае необходимости, могут регулироваться оператором [9].

На этапе высокочастотной фильтрации по времени значение для по умолчанию устанавливается равным 365 дням. Таким образом, общий интервал усреднения по времени равен одному году и, в случае необходимости, также может регулироваться оператором [9].

При формировании атмосферных фазовых экранов используются только пиксели со значениями когерентности по ансамблю изображений (21) не ниже 0,5 [10].

За счет использования системы частично перекрывающихся атмосферных окон в модуле PS заложена возможность обработки изображений с размерами, превышающими 5 x 5 км². При этом возникают потенциальные возможности для последующего проведения пространственной интерполяции рассчитанных атмосферных искажений с целью корректного учета эффекта нелинейности атмосферных искажений в пространстве. Поскольку для направления наклонной дальности использовалась избыточная дискретизация, перекрытие атмосферных окон для этого направления выше, чем для направления по азимуту [9].

В связи со специфическими особенностями метода атмосферной коррекции (не выполняется развертка фазы), при проведении оценки точности получаемых значений скорости смещения и остаточной высоты PS используется алгоритм, основанный на использовании не только распределения значений нормальных компонент базовой линии и временных интервалов между съемками опорного и парных изображений, но и значений когерентности и плотности PS [10].

Перед выполнением операции устранения фазового сдвига интерферограмм (см. раздел 2.1.3) с использованием методики простой периодограммы (13) проводится предварительная оценка скорости смещения и остаточной высоты PSC_MIN. Рассчитанные на их основе значения фазы учитываются при проведении операции устранения фазового пьедестала на интерферограммах [10]. Предварительная оценка скорости смещения PSC_MIN выполняется до атмосферной коррекции; значение скорости после атмосферной коррекции может отличаться от истинного, что приводит к возникновению общего сдвига поля скоростей [9]. После формирования расширенного набора PS проводится коррекция этого сдвига с использованием опорного PS, для которого априори известно истинное значение скорости смещения [9]. С целью обеспечения более точной коррекции поля скоростей предусмотрена возможность использования набора опорных PS [9].

Физический смысл процедуры состоит в следующем. Поскольку реализованный в модуле PS метод использует значения фазы, свернутые по модулю 2π, оказывается невозможным применение процедуры прецизионной коррекции орбитальных параметров (Refinement and Re-flattening), используемой в рамках традиционной и дифференциальной интерферометрии [9]. Следовательно, в интерферограммах сохраняются соответствующие фазовые искажения. При этом, поскольку ошибки орбитальных параметров у разных парных изображений различаются, фазовые искажения у них также различны. Искажения данного типа интерпретируются программой как дополнительные сдвиги PS, зависящие от координат. При случайном возникновении линейного временного тренда программа будет ошибочно интерпретировать эту компоненту фазовых искажений в качестве дополнительной компоненты скорости PS, т.е. дополнительного сдвига поля скоростей, зависящего от координат. Ввод априори известных значений скорости смещения для нескольких опорных PS (распределенных по изображению) позволяет осуществить пространственную интерполяцию для корректирующих аддитивных поправок.

4. Заключение

На основе подробного анализа литературных источников и программной документации пакета SARscape представлено детальное описание ключевых моментов двух наиболее распространенных вариантов метода PS, отмечены основные особенности метода, реализованного в модуле постоянных рассеивателей программного пакета SARscape.

Проведенные теоретические исследования легли в основу эксперимента по изучению практических возможностей метода PS на примере программного пакета SARscape с использованием тестового набора данных РСА ASAR/ENVISAT.

Литература

1. Феоктистов А.А., Захаров А.И., Денисов П.В., Гусев М.А. Перспективы разработки комплекса интерферометрической и дифференциально-интерферометрической обработки данных российских космических радиолокаторов с синтезированной апертурой // Современные проблемы дистанционного зондирования Земли из космоса: Сб. науч. ст. – М.: ООО «ДоМира», 2011. – Т. 8. – Номер 2. – С. 310-317.

2. Феоктистов А.А., Захаров А.И., Денисов П.В., Гусев М.А. Основные результаты интерферометрической обработки данных космических радиолокаторов с синтезированной апертурой X и L диапазонов // Современные проблемы дистанционного зондирования Земли из космоса: Сб. науч. ст. – М.: ООО «ДоМира», 2012. – Т. 9. – № 2. – С. 106-110.

3. Феоктистов А.А., Захаров А.И., Денисов П.В., Гусев М.А. Анализ предельных возможностей оценки деформации земной поверхности в зоне землетрясения в Японии 11.03.2011 г. по данным РСА ASAR/ENVISAT с использованием программного пакета SARscape // Материалы V Всероссийской научной конференции «Радиофизические методы в дистанционном зондировании сред». – Муром, 26-28 июня 2012 г. – (CD-ROM). – С. 258-263.

4. Феоктистов А.А., Денисов П.В., Гусев М.А. Практический опыт интерферометрической и дифференциальной интерферометрической обработки данных РСА COSMO-SkyMed, ALOS/PALSAR и ASAR/ENVISAT // Материалы IX научно-технической конференции "Системы наблюдения, мониторинга и дистанционного зондирования Земли". Геленджик. 17-21 сентября 2012 г. – М.: МНТОРЭС им. А.С. Попова, филиал ФГУП "ГНПРКЦ "ЦСКБ-ПРОГРЕСС" – НПП "ОПТЭКС", 2012. – С. 240-244.

5. Захаров А.И., Яковлев О.И, Смирнов В.М. Спутниковый мониторинг Земли. Радиолокационное зондирование поверхности // М.: КРАСАНД, 2012. – 248 С.

6. Ferretti, A., Prati, C. and Rocca, F., 2000. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry // IEEE Transactions on Geoscience and Remote Sensing, 38, pp. 2202-2212.

7. Ferretti, A., Prati, C. and Rocca, F., 2001. Permanent scatterers in SAR interferometry // IEEE Transactions on Geoscience and Remote Sensing, 39, pp. 8‑20.

8. Andrew Hooper, Howard Zebker, Paul Segall, and Bert Kampes. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers // Geophisical Research Letters, vol. 31, L23611, doi:10.1029/2004GL021737, 2004

9. Exploring the SARscape Modulus for ENVI // ITT Visual Information Slutions. Pearl East Circle. Boulder CO. – 2010. – 223 P.

10. Defilippi M. Private communication.

11. Назарян А.Н. Оценка возможностей РСА-интерферометрии в задачах геоэкологии и оценки геоопасности // Диссертация на соискание ученой степени кандидата физ.-мат. наук. М.: МГУ, 2008. – С. 120.

12. Брыксин В.М., Филатов А.В., Евтюшкин А.В. Использование радарных изображений и DINSAR-PSINSAR технологии для мониторинга Западной Сибири и Арктики // Журнал радиоэлектроники [электронный журнал], 2012. – №6. URL: http://jre.cplire.ru/jre/jun12/6/text.html

13. Bamler R. The SRTM Mission – A World-Wide 30 m Resolution DEM from SAR Interferometry in 11 Days // Photogrammetric Week, 1999, P. 145-154.