|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2001 |
 |
ВЛИЯНИЕ ИМПЕДАНСНОЙ ПОВЕРХНОСТИ КРУГОВОГО ЦИЛИНДРА
НА ПОЛЕ РАДИАЛЬНОГО ЭЛЕКТРИЧЕСКОГО ДИПОЛЯ
М. Ю. Звездина
Ростовский военный институт ракетных войск
Получена 11 июля 2001 г.
Приводятся соотношения для вычисления поля радиального электрического диполя, расположенного вблизи импедансного кругового цилиндра. Анализируются закономерности распределения поля в ближней и дальней зонах для случаев поверхности кругового цилиндра с изотропным и анизотропным импедансом. Приводятся результаты исследований влияния импедансных свойств поверхности кругового цилиндра на распределение возбуждаемых радиальным диполем поверхностных электрических токов.
Развитие современной радиоэлектроники предъявляет к антенно-фидерным устройствам высокие требования, связанные с наиболее полной реализацией их потенциальных возможностей [1-3]. Одним из направлений решения данной задачи является использование импедансных свойств поверхности несущих конструкций для формирования требуемого распределения поля в пространстве как в ближней, так и в дальней зонах. Поверхностный импеданс связан с такими конструктивными характеристиками несущей поверхности, как толщина и диэлектрическая проницаемость слоя диэлектрика (так называемый изотропный импеданс), толщина слоя плазмы или глубина канавок ребристой структуры (анизотропный импеданс) и т.д. [2-10].
Возбуждение импедансных поверхностей для ряда случаев рассмотрено в работах [2, 4-9, 11-17]. В материалах статей [18-20] были рассмотрены варианты продольной и поперечной относительно образующей импедансного кругового цилиндра ориентации электрического диполя, расположенного вблизи него. В работе [21] приведены общие соотношения, описывающие поле произвольно ориентированного диполя. Однако вопросы, связанные с исследованием влияния анизотропного поверхностного импеданса кругового цилиндра на поле расположенного вблизи него радиального диполя, требуют более детального рассмотрения.
Целью статьи является решение задачи о нахождении поля радиального диполя, расположенного вблизи анизотропного импедансного кругового цилиндра.
Рассмотрим однородный и безграничный вдоль оси
![]() круговой цилиндр
радиуса
круговой цилиндр
радиуса
![]() с
тензором поверхностного импеданса
с
тензором поверхностного импеданса
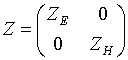 (
(![]() ‑ волновые сопротивления в классе Е-
и Н-волн соответственно), возбуждаемый радиальным электрическим
диполем с длиной плеча
‑ волновые сопротивления в классе Е-
и Н-волн соответственно), возбуждаемый радиальным электрическим
диполем с длиной плеча
![]() , центр которого расположен в точке Q, определяемой в цилиндрической системе
координат
, центр которого расположен в точке Q, определяемой в цилиндрической системе
координат
![]() радиус-вектором
радиус-вектором
![]() . Ток в диполе с амплитудой
. Ток в диполе с амплитудой
![]() определяется
выражением
определяется
выражением
Множитель
![]() , описывающий зависимость всех величин от
времени, здесь и далее опущен.
, описывающий зависимость всех величин от
времени, здесь и далее опущен.
При использовании соотношений, приведенных в [21] для произвольной ориентации диполя, несложно записать выражения для компонент поля радиального диполя.
Для однородной вдоль оси 0z системы поле (падающее, рассеянное и полное) может быть представлено, как и в [5], в виде бесконечного спектра цилиндрических волн, распространяющихся в радиальном направлении и модулированных по оси 0z:
где
![]() ;
;
![]() ;
;
![]() ‑ радиус-вектор произвольной точки P; i – мнимая единица. Выражения для продольных и поперечных компонент
падающего поля при таком представлении приведены в [5,
21]. Деформация
первоначального контура интегрирования, подробно описанная в [21-23], позволяет
в интеграле, описывающем рассеянное поле, выделить вычеты. При этом продольные
компоненты рассеянного поля представляются в виде непрерывно-дискретного
спектра
‑ радиус-вектор произвольной точки P; i – мнимая единица. Выражения для продольных и поперечных компонент
падающего поля при таком представлении приведены в [5,
21]. Деформация
первоначального контура интегрирования, подробно описанная в [21-23], позволяет
в интеграле, описывающем рассеянное поле, выделить вычеты. При этом продольные
компоненты рассеянного поля представляются в виде непрерывно-дискретного
спектра
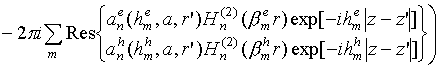 ,
,
где
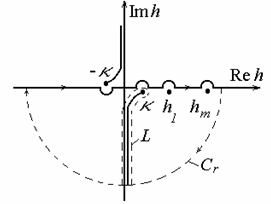
![]() ‑ функция Ганкеля 2-го рода n-го порядка; L ‑ петлеообразный
контур (рис.1);
‑ функция Ганкеля 2-го рода n-го порядка; L ‑ петлеообразный
контур (рис.1);
![]() ‑ вычеты подынтегрального выражения
(3), взятые в полюсах, найденных из условия равенства нулю знаменателей коэффициентов
‑ вычеты подынтегрального выражения
(3), взятые в полюсах, найденных из условия равенства нулю знаменателей коэффициентов
![]() ,
поскольку в рассматриваемой полуплоскости функция Ганкеля нулей не имеет [23];
,
поскольку в рассматриваемой полуплоскости функция Ганкеля нулей не имеет [23];
![]() ‑
поперечное волновое число, связанное в предположении о малых потерях в
импедансной среде с продольным
волновым числом h и волновым числом свободного пространства
‑
поперечное волновое число, связанное в предположении о малых потерях в
импедансной среде с продольным
волновым числом h и волновым числом свободного пространства
![]() (
(![]() ‑ длина волны)
соотношением
‑ длина волны)
соотношением
![]() ;
;
![]() ‑ поперечные волновые числа,
соответствующие
m-му полюсу для случая Е- и Н-волновых сопротивлений. Выбор знака реальной и мнимой части
‑ поперечные волновые числа,
соответствующие
m-му полюсу для случая Е- и Н-волновых сопротивлений. Выбор знака реальной и мнимой части
![]() определяется
из условий сходимости интегралов (3) и подробно рассмотрен в работах [2,
11, 21-23].
определяется
из условий сходимости интегралов (3) и подробно рассмотрен в работах [2,
11, 21-23].
Рис.1. Контур интегрирования
Коэффициенты дифракции
![]() для
радиального диполя, найденные на основе результатов работы [21], описываются
выражениями:
для
радиального диполя, найденные на основе результатов работы [21], описываются
выражениями:
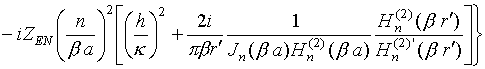 ,
,
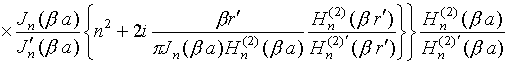 ;
;
![]() ‑ соответственно производные функции Бесселя n-го порядка и
функции Ганкеля 2-го рода n-го
порядка;
‑ соответственно производные функции Бесселя n-го порядка и
функции Ганкеля 2-го рода n-го
порядка;
![]() ,
,
![]() ;
;
![]() Ом – волновое
сопротивление свободного пространства.
Ом – волновое
сопротивление свободного пространства.
Анализ соотношений (4)-(8) показывает, что на рассматриваемом
контуре интегрирования полюсы определяются из условия равенства нулю выражения
(8) и зависят от импедансных свойств поверхности. В найденном спектре корней
собственные числа
![]() , лежащие на действительной полуоси (
, лежащие на действительной полуоси (![]() ,
,
![]() ), описывают
быстрые волны излучения, а
), описывают
быстрые волны излучения, а
![]() , лежащие на мнимой полуоси (
, лежащие на мнимой полуоси (![]() ,
,
![]() ) ‑
поверхностные волны, распространяющиеся в зависимости от выполнения условия
) ‑
поверхностные волны, распространяющиеся в зависимости от выполнения условия
![]() либо в
поперечном относительно образующей цилиндра направлении, либо вдоль образующей
цилиндра. Выражения для вычетов, взятые в полюсах, могут быть легко получены [24], однако имеют громоздкий вид и здесь не приводятся.
либо в
поперечном относительно образующей цилиндра направлении, либо вдоль образующей
цилиндра. Выражения для вычетов, взятые в полюсах, могут быть легко получены [24], однако имеют громоздкий вид и здесь не приводятся.
Запишем компоненты электромагнитного поля излучения, возбуждаемого
в точке P радиальным электрическим диполем,
расположенным вблизи бесконечного импедансного кругового цилиндра (в точке Q), в случае
![]() (поле в ближней зоне):
(поле в ближней зоне):

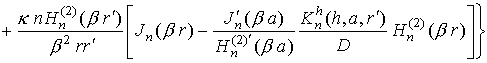 ,
,
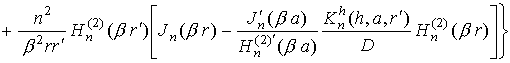 ,
(13)
,
(13)
Выражения для поперечных компонент поля найдены при использовании известных соотношений [5], связывающих поперечные составляющие поля с продольными.
Компоненты электромагнитного поля в дальней зоне получаются из соотношений (3)-(14) при вычислении интеграла методом перевала, подробно описанном в [5]. Опуская промежуточные выкладки, запишем результат преобразований:
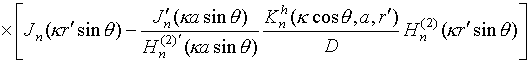 ,
,
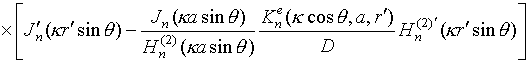 ,
,
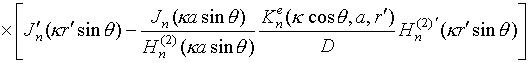 ,
,
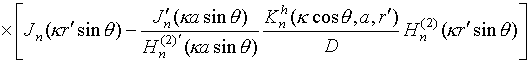 ,
,
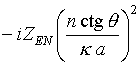 .
.
В
соотношениях (15)‑(18) 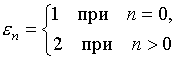 ‑ числа Неймана.
‑ числа Неймана.
Интегрирование методом перевала второго слагаемого из (3), описывающего поверхностные волны, для случая сосредоточенного источника конечной длины, расположенного вблизи начала координат, как показано в [22], приводит к выражению, существующему в интервале, который стремится к нулю. В связи с этим данное слагаемое опущено. Таким образом, соотношения (15)-(19) описывают поле излучения в дальней зоне.
Выполним
анализ данных выражений. В случае изотропного импеданса полученные соотношения
могут быть легко сведены к выражениям, приведенным в [25] и полученным другим
способом. Для идеально проводящего цилиндра (![]() ) особые точки, как следует из
выражений (8), совпадают с точками ветвления
) особые точки, как следует из
выражений (8), совпадают с точками ветвления
![]() . Поверхностные волны
отсутствуют, и соотношения (3)-(19) совпадают с соотношениями, приведенными в [4,
5, 23]. В случае продольной ребристой структуры
. Поверхностные волны
отсутствуют, и соотношения (3)-(19) совпадают с соотношениями, приведенными в [4,
5, 23]. В случае продольной ребристой структуры
![]() [5]. Коэффициенты
[5]. Коэффициенты
![]() и
и
![]() , как и для
случая поперечного диполя [19], при данном значении импеданса определяются
зависимостями
, как и для
случая поперечного диполя [19], при данном значении импеданса определяются
зависимостями
т.е.
для продольной компоненты электрического поля радиального диполя поверхность
является идеально проводящей, а ее импедансные свойства, связанные с элементом
тензора
![]() ,
проявляются только по отношению к продольной компоненте магнитного поля.
,
проявляются только по отношению к продольной компоненте магнитного поля.
Для
поперечной ребристой структуры
![]() [6]. При этом ни один из коэффициентов
[6]. При этом ни один из коэффициентов
![]() и
и
![]() не обращается
в единицу и импедансные свойства поверхности проявляются для продольных
компонент как электрического, так и магнитного полей.
не обращается
в единицу и импедансные свойства поверхности проявляются для продольных
компонент как электрического, так и магнитного полей.
Поскольку в работе [25] уже исследовался вопрос влияния импедансных свойств поверхности кругового цилиндра на диаграмму направленности радиального диполя, проанализируем влияние параметров импеданса на распределение поверхностного электрического тока, возбуждаемого данным источником.
Результаты
численных исследований приведены на рис.2-8. Радиус цилиндра при проведении
вычислительного эксперимента принимался равным
![]() , удаление диполя от оси цилиндра
, удаление диполя от оси цилиндра
![]() ,
,
![]() и
и
![]() изменялись в
пределах
изменялись в
пределах
![]() и
и
![]() .
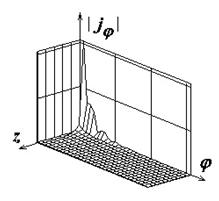
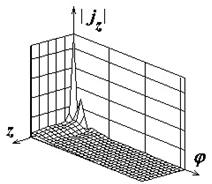
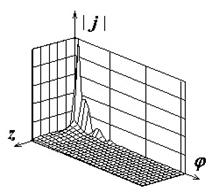
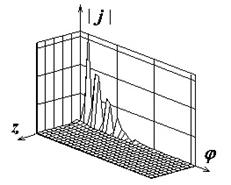
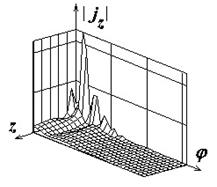
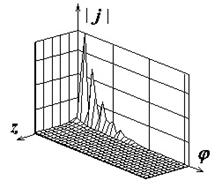
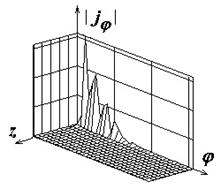
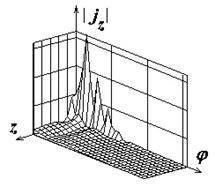
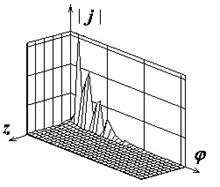
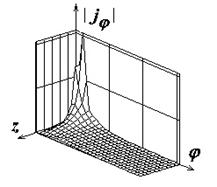
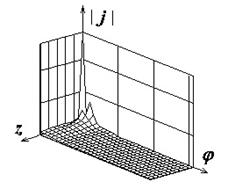
Поля с индексами "а", "б" и "в" на рис.2-8
иллюстрируют распределения амплитуд компонент поверхностного тока
.
Поля с индексами "а", "б" и "в" на рис.2-8
иллюстрируют распределения амплитуд компонент поверхностного тока
![]() ,
,
![]() , а также
модуля полного тока соответственно. Амплитуды компонент тока нормированы к
максимальному значению полного тока, возбуждаемого на идеально проводящем
круговом цилиндре. Исследовались следующие способы реализации импедансных
граничных условий: идеально проводящий металлической поверхности
, а также
модуля полного тока соответственно. Амплитуды компонент тока нормированы к
максимальному значению полного тока, возбуждаемого на идеально проводящем
круговом цилиндре. Исследовались следующие способы реализации импедансных
граничных условий: идеально проводящий металлической поверхности
![]() (рис.2); продольной
ребристой структуре
(рис.2); продольной
ребристой структуре
![]() ,
,
![]() (рис.3); поперечной ребристой структуре
(рис.3); поперечной ребристой структуре
![]() ,
,
![]() (рис.4);
тонкому слою диэлектрика ‑ с изотропным мнимым импедансом (без учета
потерь на поглощение)
(рис.4);
тонкому слою диэлектрика ‑ с изотропным мнимым импедансом (без учета
потерь на поглощение)
![]() ,
,
![]() (рис.5); изотропным импедансом с учетом
поглощения
(рис.5); изотропным импедансом с учетом
поглощения
![]() (рис.6);
а также продольной ребристой структуре с учетом поглощения
(рис.6);
а также продольной ребристой структуре с учетом поглощения
![]() (рис.7); поперечной
ребристой структуре с учетом поглощения
(рис.7); поперечной
ребристой структуре с учетом поглощения
![]() (рис.8).
(рис.8).
Анализ
объемных графиков компонент плотности поверхностного тока показывает, что
компоненты тензора поверхностного импеданса по-разному влияют на векторные
составляющие плотности поверхностного тока. Так, наличие анизотропного импеданса
с
![]() составляющей
при условии равенства нулю второй компоненты тензора приводит к резкому
изменению структуры поля: возрастает с 60% для идеально проводящей поверхности
цилиндра до 90% при
составляющей
при условии равенства нулю второй компоненты тензора приводит к резкому
изменению структуры поля: возрастает с 60% для идеально проводящей поверхности
цилиндра до 90% при
![]() или
или
![]() продольная составляющая вектора
напряженности магнитного поля, а, следовательно, растет и
продольная составляющая вектора
напряженности магнитного поля, а, следовательно, растет и
![]() -компонента плотности
поверхностного тока. Наблюдается смещение точки максимума
-компонента плотности
поверхностного тока. Наблюдается смещение точки максимума
![]() -компоненты тока в
поперечной плоскости. Так, если для идеально проводящей поверхности максимум
данной компоненты находится в ближайшей к диполю точки поверхности цилиндра (
-компоненты тока в
поперечной плоскости. Так, если для идеально проводящей поверхности максимум
данной компоненты находится в ближайшей к диполю точки поверхности цилиндра (![]() ), то
анизотропный импеданс с
), то
анизотропный импеданс с
![]() составляющей приводит к ее смещению на
составляющей приводит к ее смещению на
![]() . Поскольку
максимум излучения радиального диполя совпадает с направлением, касательным к
поверхности цилиндра, то в поперечной плоскости наблюдаются значительные
осцилляции тока. Появление анизотропного импеданса с
. Поскольку
максимум излучения радиального диполя совпадает с направлением, касательным к
поверхности цилиндра, то в поперечной плоскости наблюдаются значительные
осцилляции тока. Появление анизотропного импеданса с
![]() составляющей (
составляющей (![]() и
и
![]() ) при условии
равенств нулю второй компоненты тензора приводит к возрастанию (в 4-5 раз)
поперечной составляющей вектора напряженности магнитного поля и росту амплитуды
) при условии
равенств нулю второй компоненты тензора приводит к возрастанию (в 4-5 раз)
поперечной составляющей вектора напряженности магнитного поля и росту амплитуды
![]() -компоненты
плотности поверхностного тока. Амплитуда второй компоненты уменьшается и
составляет около 10% от максимума амплитуды аналогичной компоненты тока,
возбуждаемой на идеально проводящем цилиндре. Расположение точки максимума
амплитуд компонент тока совпадает со случаем нулевого импеданса поверхности:
для
-компоненты
плотности поверхностного тока. Амплитуда второй компоненты уменьшается и
составляет около 10% от максимума амплитуды аналогичной компоненты тока,
возбуждаемой на идеально проводящем цилиндре. Расположение точки максимума
амплитуд компонент тока совпадает со случаем нулевого импеданса поверхности:
для
![]() -компоненты
плотности поверхностного тока точка смещена, поскольку в поперечной плоскости
продольная компонента вектора напряженности магнитного тока описывается законом
-компоненты
плотности поверхностного тока точка смещена, поскольку в поперечной плоскости
продольная компонента вектора напряженности магнитного тока описывается законом
![]() , а
для
, а
для ![]() -компоненты
‑ находится непосредственно под диполем (поперечная компонента вектора
напряженности магнитного поля описывается законом
-компоненты
‑ находится непосредственно под диполем (поперечная компонента вектора
напряженности магнитного поля описывается законом
![]() ). Изменение структуры поля при
изотропном импедансе поверхности зависит от наличия активной составляющей. При
чисто мнимом импедансе структура поля аналогична случаю анизотропного импеданса
с
). Изменение структуры поля при
изотропном импедансе поверхности зависит от наличия активной составляющей. При
чисто мнимом импедансе структура поля аналогична случаю анизотропного импеданса
с
![]() компонентой
тензора. Появление активной составляющей в функции, описывающей поверхностный
импеданс, приводит к изменению структуры поля, аналогичному случаю
анизотропного импеданса с
компонентой
тензора. Появление активной составляющей в функции, описывающей поверхностный
импеданс, приводит к изменению структуры поля, аналогичному случаю
анизотропного импеданса с
![]() составляющей тензора.
составляющей тензора.
В
продольной плоскости амплитуда тока резко (экспоненциально) затухает. Для ненулевого
импеданса при
![]() наблюдается незатухающая волна. Радиальный
диполь является точечным источником, неэффективно возбуждающим поверхностную
волну (амплитуда составляет 1-5% относительно максимального значения полного
тока, возбуждаемого на идеально проводящем круговом цилиндре и охватывает полосу
шириной
наблюдается незатухающая волна. Радиальный
диполь является точечным источником, неэффективно возбуждающим поверхностную
волну (амплитуда составляет 1-5% относительно максимального значения полного
тока, возбуждаемого на идеально проводящем круговом цилиндре и охватывает полосу
шириной
![]() ).
).
Таким образом, приведенные соотношения являются решением задачи о нахождении поля радиального диполя, расположенного вблизи импедансного кругового цилиндра. Выражения, описывающие коэффициенты дифракции, позволяют исследовать случаи как изотропного, так и анизотропного поверхностного импеданса, а также условия возникновения поверхностных волн.
|
а |
б |
в |
|
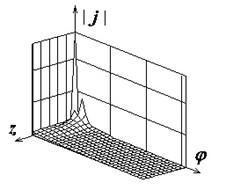
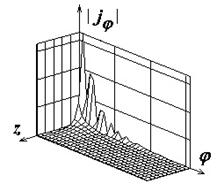
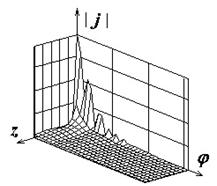
Рис.2. Распределение плотности поверхностного электрического тока на идеально проводящем круговом цилиндре |
||
|
а |
б |
в |
|
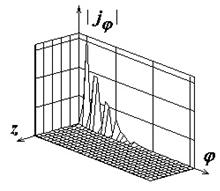
Рис.3. Распределение плотности поверхностного электрического тока на импедансном круговом цилиндре с параметрами
|
||
|
а |
б |
в |
|
Рис.4. Распределение плотности поверхностного электрического тока на импедансном круговом цилиндре с параметрами
|
||
|
а |
б |
в |
|
Рис.5. Распределение плотности поверхностного электрического тока на импедансном круговом цилиндре с параметрами
|
||
|
а |
б |
в |
|
Рис.6. Распределение плотности поверхностного электрического тока на импедансном круговом цилиндре с параметрами
|
||
|
а |
б |
в |
|
Рис.7. Распределение плотности поверхностного электрического тока на импедансном круговом цилиндре с параметрами
|
||
|
а |
б |
в |
|
Рис.8. Распределение плотности поверхностного электрического тока на импедансном круговом цилиндре с параметрами
|
||
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Проблемы антенной техники. /Под ред. Л.Д. Бахраха, Д.И. Воскресенского. – М.: Радио и связь, 1989. – 368с.
2. Кюркчан А.Г. Возбуждение нитью тока периодической ребристой структуры, обладающей свойствами искусственно жесткой поверхности // Радиотехника и электроника. 1999. Т.44. №7. С.787-793.
3. Бененсон Л.С., Кюркчан А.Г. Метод развязки антенн при помощи периодических структур // Радиотехника. 1995. №12. С. 62-69.
4. Уэйт Д.Р. Электромагнитное излучение из цилиндрических структур. – М.: Сов. Радио, 1963. – 240с.
5. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. – М.: Радио и связь, 1983. – 296с.
6. Терешин О.Н., Седов В.М., Чаплин А.Ф. Синтез антенн на замедляющих структурах. – М.: Связь, 1989. – 136с.
7. Васильев Е.Н. Возбуждение тел вращения. – М.: Радио и связь, 1987. – 272с.
8. Graglia R.D., Uslenghi P.L.E., Vitiello K., D’Elia U. Electromagnetic scattering for oblique incidence on impedance bodies of revolution // IEEE Trans. Antennas and Propag. 1995. V.43. №1. P.11-26.
9. Papousek W., Schnizer B. Surface impedance concepts of electromagnetic wave propagation in layered isotropic and anisotropic media // Radio Sci. 1982. V.17. P.1159-1167.
10. Ammori H., He S. Effective impedance boundary conditions for an inhomogeneous thin layer on a curved metallic surface // IEEE Trans. Antennas and Propag. 1998. V.46. №5. P. 710-715.
11. Каценеленбаум Б.З. Высокочастотная электродинамика. – М.: Наука, 1966. – 240с.
12. Звягинцев А.А., Батраков Д.О. Дифракция на эллиптическом импедансном цилиндре // Изв. вуз. Радиофизика. 1989. Т.32. №9. С.1125-1131.
13. Osipov A., Hongo K., Kaayashi H. High-frequency scattering of an oblique incidence plane electromagnetic wave by an impedance cylinder // AP-2000, Davos, Switzerland. April, 2000. Advanced Technical Programs, p.8.
14. Tenneti R. Plane scattering by a corrugated conducting cylinder at oblique incidence //IEEE Trans. Antennas and Propag. 1988. V.36. № 8. P.1184-1188.
15. Graglia R.D., Uslenghi P.L.E. Surface currents on impedance bodies of revolution //IEEE Trans. Antennas and Propag. 1988. V.36. №9. P.1313-1317.
16. Hussar P.E. A uniform GTD treatment of surface diffraction by impedance and coated cylinders //IEEE Trans. Antennas and Propag. 1998. V.46. №7. P.998-1008.
17. Su T., Ling H. Determining the equivalent impedance boundary condition for corrugated coating based on the genetic algorithm //IEEE Trans. Antennas and Propag. 2000. V.48. №3. P.374-383.
18. Габриэльян Д.Д., Звездина М.Ю., Костенко П.И. Возбуждение импедансной поверхности цилиндра продольным электрическим диполем // Эл. ж-л "Журнал радиоэлектроники". 2000. №6. http://jre.cplire.ru/win/jun00/6/text.html
19. Звездина М.Ю. Поле поперечного электрического диполя, расположенного вблизи импедансного кругового цилиндра // Эл. ж-л "Журнал радиоэлектроники". 2000. №9. http://jre.cplire.ru/win/sep00/2/text.html
20. Габриэльян Д.Д., Звездина М.Ю., Звездина Ю.А. и др. Возбуждение импедансной поверхности цилиндра поперечным электрическим диполем // Эл. ж-л "Журнал радиоэлектроники". 2000. №10. http://jre.cplire.ru/win/oct00/6/text.html
21.Звездина М.Ю. Влияние импедансной поверхности кругового цилиндра на поле произвольно ориентированного диполя //Эл. ж-л "Журнал радиоэлектроники". 2001. №6. http://jre.cplire.ru/jre/jun01/5/text.html
22. Шевченко В.В. Плавные переходы в открытых волноводах. Введение в теорию – М.: Наука, 1969. – 192с.
23. Кравченко В.А. Поле радиального вибратора, расположенного вблизи идеально проводящего кругового цилиндра // Радиотехника. 1973. Т.28. №8. С.43-50.
24. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. ‑ М.: Мир, 1964. ‑ 428 с.
25. Габриэльян Д.Д., Звездина М.Ю. Влияние импедансной поверхности кругового цилиндра на диаграмму направленности электрического диполя // Радиотехника и электроника. 2000. Т.45. №10. С.1194-1197.
Автор:
Звездина Марина Юрьевна – к.т.н., РВИ РВ, email: zvezd@jeo.ru
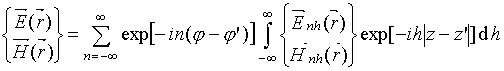 , (2)
, (2)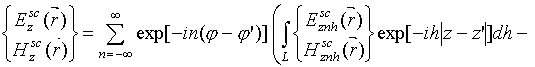 (3)
(3)
 ,
(4)
,
(4)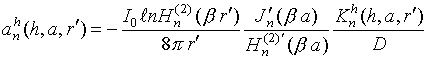 ,
(5)
,
(5)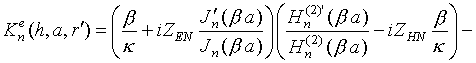 (6)
(6)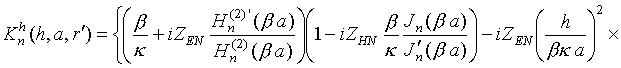 (7)
(7) , (8)
, (8) ,
,
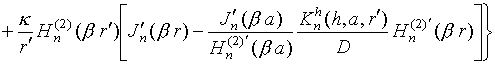 ,
(10)
,
(10) (11)
(11) ,
,
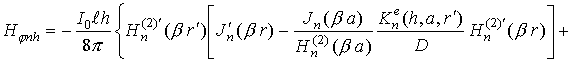
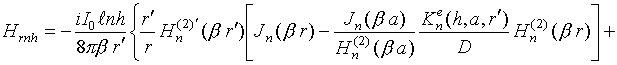
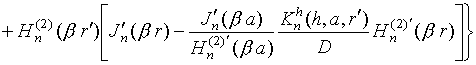 .
(14)
.
(14)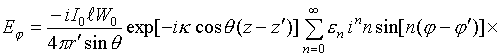 (15)
(15) (16)
(16) (17)
(17)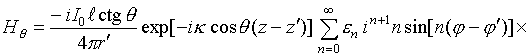 (18)
(18)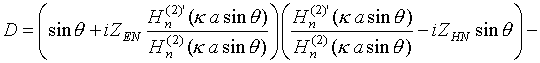
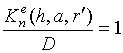 ,
,
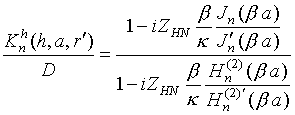 ,
(20)
,
(20)