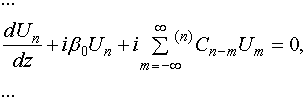УДК 621.396.67

ВОЛНЫ СИСТЕМЫ СВЯЗАННЫХ ИНТЕГРАЛЬНЫХ ДИЭЛЕКТРИЧЕСКИХ ВОЛНОВОДОВ

С. Е. Банков, М. В. Весник

ИРЭ им. В.А. Котельникова РАН

Статья получена 20 мая 2014 г.

Аннотация. Рассмотрена бесконечная система бесконечных связанных интегральных диэлектрических волноводов. Исследованы трехслойные интегральные диэлектрические волноводы, состоящие из центральной области в виде диэлектрической пластины, расположенной между двух металлических экранов и двух внешних областей, образованных двумерными периодическими решетками сквозных отверстий в указанной диэлектрической пластине. Изучены основные собственные волны системы связанных волноводов путем численного решения электродинамической задачи методом конечных элементов. Получены частотные зависимости их коэффициентов замедления и линейных коэффициентов связи. Рассмотрены структуры с решетками с прямоугольной и гексагональными сетками. Предложена приближенная модель исследуемой структуры, использующая усредненную диэлектрическую проницаемость среды с периодической решеткой.

Ключевые слова: связанные волноводы, диэлектрический волновод, искусственная среда.

Abstract. An infinite system of infinite coupled integrated dielectric waveguides is considered. Integrated waveguides containing dielectric slab between two metal screens as a central region and two outer regions formed by two-dimensional arrays of via holes in the slab are investigated. Dominant eigen modes of the waveguide system are studied with help of a numerical solution of electromagnetic problem obtained with help of a finite elements method. Frequency dependencies of eigen modes retardation factors and coupling coefficients are obtained. Structures with arrays with rectangular and hexagonal grids are considered. An approximate model of the investigated structure on the base of averaged dielectric constant of periodic media is proposed.

Keywords: coupled waveguides, dielectric waveguides, artificial media.

1. Постановка задачи

Одним из возможных подходов к техническому освоению миллиметрового и субмиллиметрового диапазонов (ММД и СМДД) является разработка устройств интегральной СВЧ оптики [1]. Такие устройства осуществляют пространственные преобразования электромагнитных полей с помощью оптических принципов и элементов: линз, зеркал, излучающих решеток и т.д. При этом все указанные элементы могут быть изготовлены в рамках единой интегральной технологии, что существенно улучшает конструктивные и экономические показатели качества устройств интегральной СВЧ оптики. Одним из важных элементов такого типа является многоканальный облучатель, который используется для облучения интегральной линзы или зеркала. С их помощью могут создаваться представляющие большой интерес многолучевые интегральные антенны ММД [2], [3].

При построении многоканальных или, как их еще называют, матричных облучателей, возникает известная проблема, которая состоит в том, что оптимальное облучение оптической системы невозможно осуществить, используя излучение из одного канала облучателя [4]. Необходимо использовать группу каналов или кластер. Возбуждение кластера возможно только при создании внутри облучателя специально организованных связей между каналами.

В работе [5] была предложена структура многоканального облучателя, использующего распределенную связь между волноводами, которые формируют его каналы. Устройство включает решетку одинаковых связанных волноводов и блок фиксированных фазосдвигателей. Схема, предложенная в работе [6], является развитием работы [5]. В ней вместо фиксированных фазосдвигателей используются неодинаковые связанные волноводы.

В работе [7] анализируется многоканальный облучатель на основе системы связанных Н – образных ДВ, которые представляют собой прямоугольные стержни, расположенные между двух металлических экранов. Такие волноводы во многих случаях более удобны в ММД, чем полые металлические волноводы.

Данная работа является продолжение работы [7]. В ней рассматривается возможность использования в многоканальных облучателях интегральных ДВ (ИДВ), образованных системой сквозных отверстий в диэлектрической пластине (см. рис. 1 а,б). Достоинством данного волновода является простота его производства, которое сводится к стандартной операции технологии печатных плат – сверлению отверстий.

Принцип функционирования такого ИДВ состоит в том, что внешние области, занятые решетками отверстий могут быть описаны с помощью эффективной диэлектрической проницаемости (ЭДП), меньшей проницаемости центральной области волновода. Концепция ЭДП не вызывает сомнений, если период решетки много меньше длины волны. Она также может быть использована для качественного описания распространения волн в ИДВ при относительно больших периодах решетки, при которых в ней имеется одна распространяющаяся волна. В многоволновом режиме представлять периодическую решетку как однородную среду невозможно.

Если исключить из рассмотрения решетки в многоволновом режиме, то с помощью концепции ЭДП нетрудно показать, что ИДВ направляет волны также как все ДВ за счет большей проницаемости сердцевины волновода по отношению к его периферии.

Следует заметить, что в ММД и особенно в его высокочастотной области весьма непросто выполнить период решетки много меньшим длины волны. Как правило, уже на частотах порядка 40 ГГц, он сравним с половиной длины волны в среде с проницаемостью диэлектрической пластины. Данное обстоятельство означает, что условия корректного применения концепции ЭДП нарушены и ее использование должно быть обосновано с помощью численных расчетов, выполненных на электродинамическом уровне строгости.

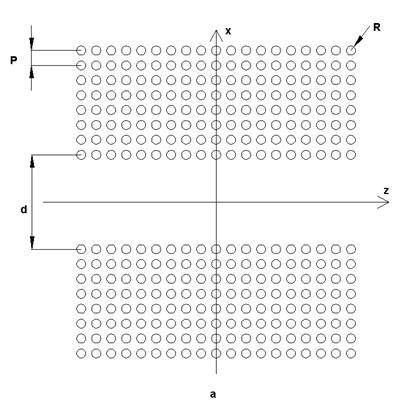
Рис. 1. ИДВ

В работах [7], [8] был предложен комплексный подход к моделированию многоканальных облучателей на основе связанных волноводов, который в качестве важного этапа включает электродинамический анализ собственных волн бесконечной системы бесконечных связанных волноводов, функционирущей в квазипериодическом режиме. В этом режиме поля в соседних периодах отличаются только фазовым сдвигом. На данном этапе определяются коэффициенты замедления основных волн системы как функции ее параметров, частоты и фазового сдвига волн в каналах. Далее с помощью полученных зависимостей находятся линейные коэффициенты связи (ЛКС) волн.

Полученные ЛКС позволяют на следующих этапах анализа многоканального облучателя использовать приближенную теорию связанных волн [9]. Ее численная реализация требует существенно меньших затрат компьютерных ресурсов, чем электродинамическое решение. При этом за счет того, что значения ЛКС находятся из относительно строгого анализа собственных волн погрешность теории связанных волн оказывается достаточно малой.

В данной работе решается задача анализа собственных волн бесконечной решетки одинаковых связанных ИДВ. Решение проводится с использованием строгого численного метода конечных элементов (МКЭ). Полученное решение обрабатывается в среде Маткад, что позволяет найти искомые коэффициенты замедления основных волн, а через них определить ЛКС.

2. Методика определения коэффициентов замедления собственных волн структуры и параметров теории связанных волн

Следует отметить, что современные средства электродинамического моделирования плохо подходят для исследования идеализированных структур, таких как бесконечный волновод и тем более, бесконечная система связанных волноводов [10]. Поэтому задача анализа ее собственных волн не может быть решена непосредственно с их помощью. Выходом из такой ситуации может быть исследование вспомогательной структуры доступной для анализа численными методами с последующей обработкой численных результатов в других программных средах, которые позволят определить искомые параметры собственных волн.

Один из возможных вариантов интересующей

нас бесконечной системы регулярных связанных ИДВ показан на рис. 2. В нем решетка отверстий радиуса имеет прямоугольную сетку с периодами . Период системы волноводов обозначен как .

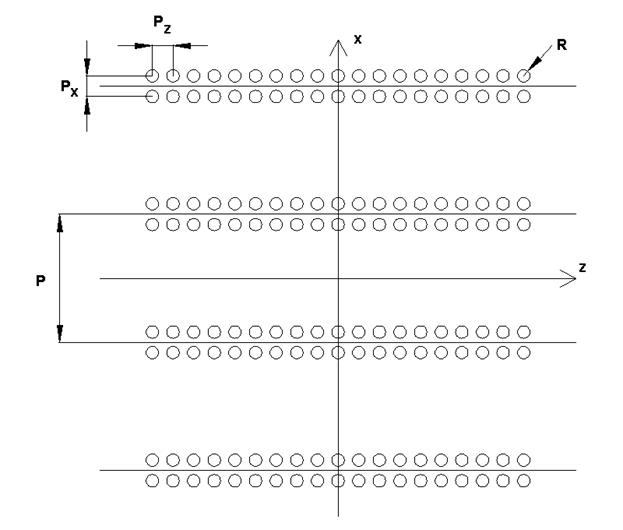
Рис. 2. Решетка связанных ИДВ

Рассмотрим далее переход от структуры на рис. 2 к другой структуре, имеющей конечные размеры и поэтому доступной для анализа численными методами. Важно при этом, чтобы результаты анализа были бы достаточными для определения параметров собственных волн исходной системы связанных ИДВ.

Выше отмечалось, что нас интересует система связанных волноводов, функционирующая в квазипериодическом режиме. Его особенностью является то, что поля в разных периодах связаны следующим образом:

, (1)

где - постоянная, определяющая фазовый сдвиг, - номер периода, определяющий его положение на оси 0х, - вектор электрического поля.

Условие периодичности (1) достаточно для того, чтобы свести анализ поля в бесконечной по оси 0х структуре к анализу одного периода. Для этого можно воспользоваться ее моделью в виде канала Флоке [10]. Она показана на рис. 3.

Рис. 3. Модель в виде канала Флоке

Данная модель содержит один период структуры. В нее также входят стенки при . На этих стенках установлены условия периодичности эквивалентные (1):

. (2)

Отметим, что аналогичные условия выполняются для вектора магнитного поля .

Таким образом, нам удалось свести анализ исходной структуры к анализу волновода ограниченного вдоль этой оси. Под собственной волной такого волновода понимаем решение граничной задачи следующего вида:

, (3)

где - постоянная распространения волны. Из формулы (3) видно, что искомая собственная волна является волной периодической по оси 0z структуры и ее поле удовлетворяет условию (3), которое аналогично условию периодичности (1).

Отметим, что диэлектрическая пластина, в которой выполнены ИДВ расположена между двух идеально проводящих экранов, а отверстия в ней сквозные. Таким образом, структура однородна вдоль оси 0у. Поэтому в ней существует решение для поля, не зависящее от координаты [11]. Это решение соответствует основной волне ИДВ и в дальнейшем мы будем интересоваться только волнами данного типа.

Постоянная распространения является функцией волнового числа . Эта зависимость имеет важное значение для определения ЛКС. Как отмечалось выше, ЛКС является параметром, описывающим связь волноводов в рамках теории связанных волн. Напомним ее основные положения.

Распространение волн в системе связанных волноводов описывается следующей системой дифференциальных уравнений:

(4)

где - амплитуды волн в волноводах, - номер волновода. В нашем случае номер волновода совпадает с номером периода. Суммирование в формуле (4) ведется по всем индексам за исключением . Параметр имеет смысл постоянной распространения уединенного волновода, а , - это ЛКС, о которых говорилось выше. Коэффициент описывает связь соседних волноводов, волноводов расположенных через один период и т.д. На практике ЛКС быстро уменьшаются с ростом . Поэтому в сумме, стоящей в соотношении (4) удерживают только члены пропорциональные .

Система уравнений (4) имеет в квазипериодическом режиме простое решение в виде бегущей волны. Ее постоянная распространения записывается следующим образом:

. (5)

Видно, что в формулу (5) входят параметры и . Их определение является одной из основных целей данной работы. Для ее достижения мы найдем зависимость постоянной распространения от переменной из решения электродинамической задачи, а затем подберем искомые параметры таким образом, чтобы отклонение формулы (5) от строгого решения было минимальным.

Модель рассматриваемой структуры в виде канала Флоке (см. рис. 3) в принципе позволяет решить поставленную задачу. Однако, использовать ее в полном объеме оказалось невозможно. Современные средства электродинамического моделирования не позволяют непосредственно решать задачи о собственных волнах периодических структур, которой является волновод изображенный на рис. 3. Поэтому находить их параметры, в частности, постоянные распространения приходится путем анализа резонансных частот резонатора, который получается из волновода при размещении в двух его сечениях при и идеально проводящих стенок, как показано на рис. 4.

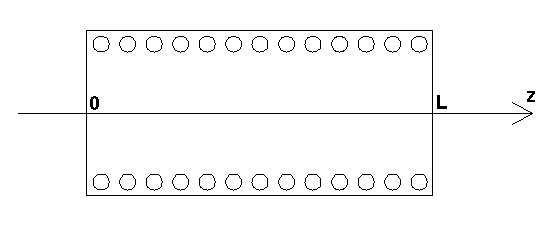
Рис. 4. Резонатор на основе канала Флоке

Важным моментом является связь резонансных частот с искомой постоянной распространения. Для ее определения считаем, что поле внутри резонатора формируется полем двух собственных волн одного типа, бегущих в противоположных направлениях.

Выберем длину резонатора равной целому числу периодов:

. (6)

В работе [12] показано, что при условии (6) характеристическое уравнение, определяющее резонансные частоты имеет следующий вид:

. (7)

Уравнение верно при выполнении дополнительного условия, о котором мы скажем ниже.

Формальное решение (7) имеет простой вид:

, (8)

Индекс называют порядком резонанса. Он равен числу полуволн, укладывающихся на длине резонатора. Отметим, что уравнение (7) и его решение (8) верны только при .

Для описания волновода удобнее вместо постоянной распространения использовать коэффициент замедления :

, (9)

где - волновое число свободного пространства. С учетом определения (9) преобразуем соотношение (8):

. (10)

При записи выражения (10) выделена зависимость коэффициента замедления и волнового числа от частоты, делающая соотношение (10) уравнением относительно частоты. Каждому порядку резонанса соответствует частота , а также значение коэффициента замедления на данной частоте .

Решение электродинамической задачи дает набор резонансных частот , используя которые с помощью соотношения (10) можно найти коэффициент замедления волны и ее постоянную распространению на указанных частотах. Найти коэффициент замедления в промежуточных частотных точках можно путем аппроксимации функции по ее значениям на частотах . Таким образом, решается поставленная задача.

Следует отметить наличие еще одного фактора, ограничивающего предложенную выше методику поиска параметров собственных волн. Он связан с тем, что современные системы электродинамического моделирования не позволяют использовать периодические граничные условия в блоке поиска резонансных частот. Допустимы лишь электрические и магнитные стенки.

Для преодоления указанной трудности мы воспользовались известным из теории антенных решеток свойством периодических структур с периодом, имеющим плоскость симметрии [13]. Известно, что поле внутри периода такой структуры при определенных значениях параметра совпадает с полем внутри волновода, который получается из исходной структуры размещением на границах периода магнитной или электрической стенок.

В нашем случае указанное свойство означает, что волновод с граничными условиями (2) на стенках при при определенных значениях можно заменить таким же волноводом, но с магнитными и электрическими стенками на границах. Резонаторы на основе таких волноводов уже могут анализироваться с помощью систем электродинамического моделирования.

В табл. 1 показаны значения параметра и тип стенки при .

Табл. 1.


0	магнитная	магнитная
	электрическая	магнитная
	электрическая	электрическая

Таким образом, анализируя резонансные частоты трех разных резонаторов, отличающихся типом стенки при мы можем найти коэффициент замедления волны при трех разных значениях постоянной распространения .

Этих значений достаточно для определения параметров теории связанных волн при учете ЛКС первого и второго порядков. Как отмечалось выше, учет ЛКС более высоких порядков нецелесообразен.

Следует также отметить, что в волноводе, который показан на рис. 3, наряду с основной волной могут распространяться волны высших типов. Они появляются на достаточно высоких частотах, которые превышают некоторую критическую частоту . Электродинамическое моделирование резонатора позволяет находить резонансные частоты, соответствующие резонансам волн как основного, так и высших типов. Выделение резонансов основной волны возможно путем анализа распределения поля колебания.

3. Задачи численного исследования

В разд. 4 будут представлены результаты численного исследования собственных волн структуры. В данном разделе мы сформулируем задачи, которые решались в ходе этого исследования.

Как отмечалось выше, необходимость изучения волн системы связанных ИДВ следует из возможности построения на ее основе технологичных многоканальных облучателей планарных линз и зеркал. Поэтому наряду с задачами исследования свойств собственных волн ставилась задача поиска структур и их параметров, пригодных для решения данной практической задачи.

В связи с этим был принят ряд ограничений на параметры ИДВ, а также диапазон частот, который можно считать рабочим. В этом диапазоне должен выполняться ряд условий. Основная волна во всем диапазоне изменения переменной должна быть распространяющейся, то есть иметь действительную постоянную распространения. Отметим, что пределы изменения параметра устанавливает неравенство:

. (11)

В рамках описанной выше методики сказанное выше означает, что волны трех волноводов из табл. 1 должны быть распространяющимися.

Следует отметить, что волновод на рис. 3, как всякий СВЧ волновод при определенных условиях может иметь несколько распространяющихся волн. Волна основного типа имеет наименьшую критическую частоту. Волны с большими критическими частотами принято называть волнами высших типов. Потребуем, чтобы наша структура функционировала в одноволновом режиме.

Сформулированные выше требования к режиму распространения волн в исследуемом волноводе типичны для большинства направляющих СВЧ структур. Следующее требование имеет специфический характер, следующий из особенностей функционирования многоканального облучателя на связанных волноводов. Потребуем соблюдения режима слабой связи между волноводами. Забегая вперед, отметим, что коэффициент замедления основной волны волновода с двумя магнитными стенками больше коэффициента замедления волновода с электрической и магнитной стенками , который, в свою очередь, больше коэффициента замедления волновода с двумя электрическими стенками . Таким образом, диапазон изменения коэффициента замедления находится в пределах от до . Этот диапазон определяет величину ЛКС. Ограничим следующим неравенством:

, (12)

где - малый параметр. В численных расчетах он был принят равным 0.25.

Необходимость ограничения ЛКС обусловлена требованием минимизации отражений от входов системы связанных волноводов при возбуждении ее одиночным волноводом.

На практике неравенство (12) определяет нижнюю частоту рабочего диапазона , так как оно перестает выполняться на частотах превышающих критическую частоту волновода с минимальным коэффициентом замедления. Отметим, что на критической частоте коэффициент замедления равен нулю. Верхняя частота рабочего диапазона равна критической частоте высшего типа волны, имеющего ее минимальной значение.

Таким образом, задача численного исследования заключается в поиске структур, удовлетворяющих сформулированным выше требованиям. При этом естественно рассматривать относительную ширину рабочего диапазона как показатель качества исследуемой системы, который необходимо увеличивать:

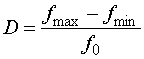, (13)

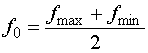Наряду с практической частью проводимого исследования, оно имело цель проверки возможности использования для описания системы ИДВ в рамках концепции ЭДП. С этой целью мы анализировали структуру изображенную на рис. 5. Она является моделью волновода на рис. 3, построенной по методу ЭДП. Методика ее анализа не отличается от описанной в разд. 3 за исключением того, что вместо области с отверстиями в модели находится однородная среда с эффективной диэлектрической проницаемостью . Проницаемость диэлектрической пластины - . Способ расчета параметра будет изложен ниже.

Рис. 5. Модель по методу ЭДП

4. Численное исследование ИДВ на основе решетки с прямоугольной сеткой

На первом этапе были рассмотрены ИДВ на основе решеток с прямоугольной сеткой. Модель резонатора, для которой решалась электродинамическая задача показана на рис. 6. В исследуемой структуре волноводы были разделены одним рядом отверстий.

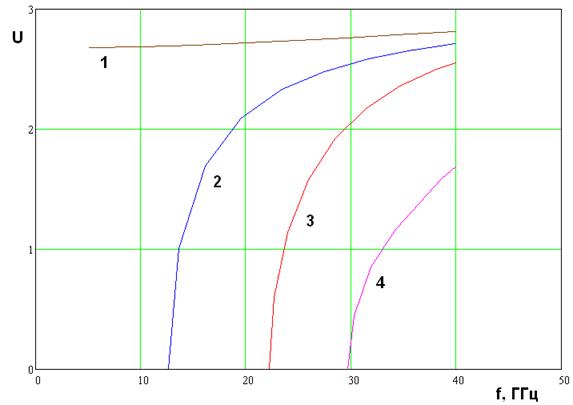
Изучим качественно поведение коэффициентов замедления основных волн трех базовых волноводов в диапазоне частот. Типичная их частотная зависимость показана на рис. 7. Кривые 1 – 4 получены для R=0.5, P=2.2, h=0.5, P_z=1.1, . Кривые 1 – 3 соответствуют коэффициентам замедления , , . Кривая 4 получена для первого высшего типа волны в волноводе с двумя магнитными стенками. Обозначим его коэффициент замедления через .

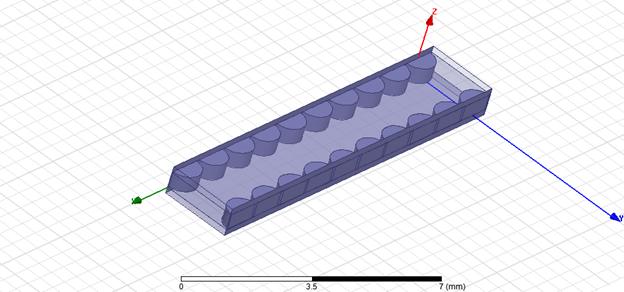
Рис. 6. Резонатор на основе ИДВ с решеткой с прямоугольной сеткой и одним рядом отверстий, разделяющих ИДВ

Рис. 7. Частотная зависимость коэффициентов замедления волн в волноводах с одним рядом цилиндров

Видно, что основная волна волновода с магнитными стенками слабо зависит от частоты. Она не имеет критической частоты и распространяется вплоть до постоянного тока.

Основные волны в волноводах с электрическими стенками и с электрической и магнитной стенками имеют критические частоты , которые равны соответственно 12.5 и 22 ГГц. Критическая частота высшего типа волны равна 29.9 ГГц. Таким образом, верхняя частота рабочего диапазона в рассматриваемом примере равна 29.9 ГГц. При этом отметим, что говорить о рабочем диапазоне в данном случае бессмысленно, так как его нижняя частота больше верхней, поскольку неравенство (12) не выполняется на частотах ниже .

Интересно рассмотреть структуру полей собственных волн. Для простоты будем называть волновод с двумя магнитными стенками ММ – волноводом, с электрической и магнитной стенками ЕМ – волноводом и волновод с двумя электрическими стенками ЕЕ – волноводом.

На рис. 8 - 10 показано распределение интенсивности электрического поля основных волн в ММ, ЕМ и ЕЕ – волноводах соответственно.

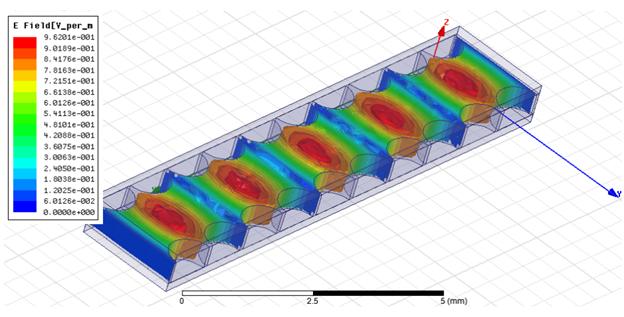
Рис. 8. Поле в ММ – волноводе

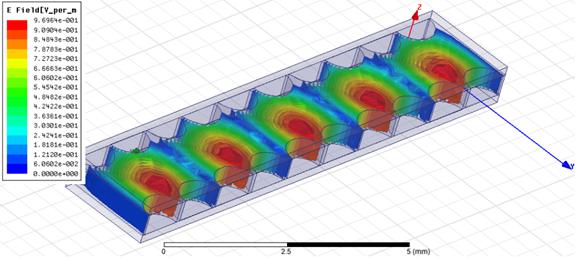
Рис. 9. Поле в ЕМ – волноводе

Рис. 10. Поле в ЕЕ – волноводе

Рис. 11. Поле волны высшего типа в ММ – волноводе

На рис. 11 показано распределение электрического поля первого высшего типа волны в ММ – волноводе.

Анализ полей собственных волн позволяет объяснить причину недопустимо сильной связи между ИДВ, которая выражается в большом отличии коэффициентов замедления , , . Дело в том, что поле слишком сильно проникает в область, в которой располагаются отверстия, формирующие среду с эффективной диэлектрической проницаемостью меньшей . Другими словами, снизить эффективную проницаемость с помощью одного ряда отверстий затруднительно.

Связь между ИДВ можно уменьшить также увеличивая расстояние между волноводами даже при относительно больших . На рис. 12 показаны частотные зависимости коэффициентов замедления волн разных волноводов со следующими параметрами: R=0.3, P=1.8, h=0.5, P_z=0.7, , расстояние между рядами цилиндров – 1.1.

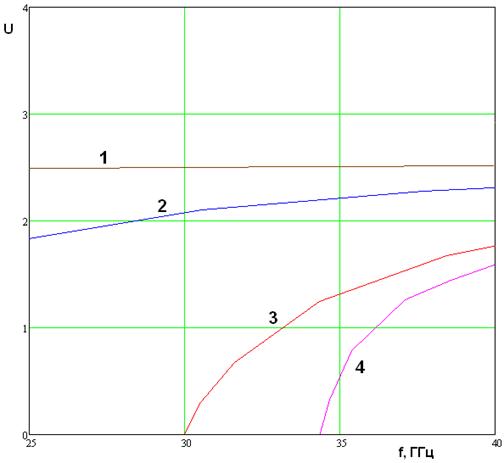
Рис. 12. Частотная зависимость коэффициентов замедления волн в волноводах с двумя рядами цилиндров

Кривые 1 – 4 соответствуют коэффициентам замедления , , , .

Видно, что картина на рис. 12 качественно мало отличается от показанной на рис. 7. Таким образом, увеличение числа рядов не привело к снижению связи между волноводами. Такой результат не должен удивлять, так как он относится только к рабочему диапазону структуры. В принципе увеличение расстояния между ИДВ рано или поздно должно привести к уменьшению связи, но нас интересует этот эффект в диапазоне частот, в котором отсутствуют высшие типы волн. Однако при увеличении указанного расстояния критическая частота наиболее опасного высшего типа волны ММ – волновода (кривая 4 на рис. 12) уменьшается и рабочий диапазон сдвигается в область низких частот, в которой коэффициент замедления в ЕЕ – волноводе недопустимо мал.

Таким образом, мы можем сделать вывод, что создание системы связанных ИДВ с достаточно малой связью с помощью искусственной среды из решетки отверстий в диэлектрической пластине с прямоугольной сеткой затруднительно. Причина данного эффекта состоит в том, что в такой решетке остается слишком много диэлектрика, который не позволяет снизить эффективную проницаемость .

Для подтверждения данного предположения целесообразно приближенно найти параметр , определяя его как среднее значение проницаемости в решетке . Для решетки с прямоугольной сеткой нетрудно получить следующее выражение для :

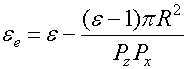, (14)

где - периоды решетки вдоль разных осей координат.

Для решетки с гексагональной сеткой средняя проницаемость определяется следующим соотношением:

, (15)

где - период гексагональной сетки.

Нетрудно убедиться, что гексагональная сетка обеспечивает более плотную упаковку цилиндров и, следовательно, меньшую эффективную проницаемость.

В силу отмеченной выше причины далее исследовались ИДВ разделенные решеткой с гексагональной сеткой. На рис. 13 показан волновод, содержащий три ряда цилиндров.

Рис. 13. ИДВ с тремя рядами цилиндров

На рис. 14 показана частотная зависимость коэффициентов замедления волн в волноводах разных типов. Кривые 1 – 5 получены для R=0.25, P=0.6, h=0.5, . Они соответствуют основным волнам ММ – волновода, МЕ – волновода, ЕЕ – волновода, высшему типу волны ММ – волновода. Кривая 5 построена исходя из условия (12). Точка ее пересечения с кривой 4 дает нижнюю границу рабочего диапазона структуры.

Рис. 14. Частотная зависимость коэффициентов замедления в волноводах с тремя рядами цилиндров

Нетрудно убедиться, что в данном примере относительный рабочий диапазон примерно равен 10%.

Таким образом, сформулированным выше условиям из всех исследованных структур удовлетворяли только ИДВ с решетками с гексагональными сетками. Получить рабочий диапазон частот существенно превышающий 10% не удалось.

Важно также отметить, что для решеток с гексагональной сеткой хорошее совпадение с точными расчетами дает приближенная методика, построенная на основе модели эффективной диэлектрической проницаемости (см. рис. 5). Численно исследовалась структура показанная на рис. 15.

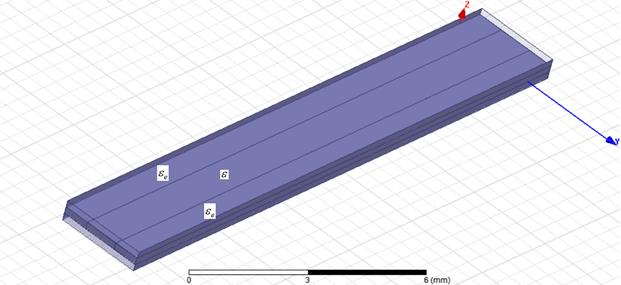
Рис. 15. Период системы ИДВ связанных через однородную эквивалентную среду

Методика ее анализа полностью аналогична описанной выше для случая ИДВ, связанных через решетку отверстий. На рис. 16 показана частотная зависимость коэффициента замедления волн в волноводах разных типов для структуры на рис. 15 с параметрами, эквивалентными структуре с гексагональной сеткой, которые приводились выше.

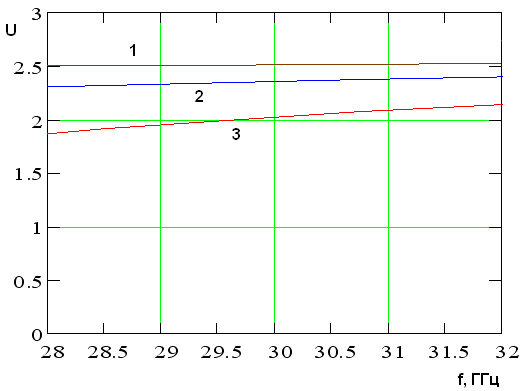
Рис. 16. Частотная зависимость коэффициентов замедления, полученная с помощью модели эффективной проницаемости

Кривые 1 – 3 соответствуют ММ, ЕМ и ЕЕ – волноводам. Сравнивая кривые 1 – 3 на рис. 16 и рис. 14, нетрудно увидеть, что они весьма близки. Таким образом, для оценки параметров достаточно сложной структуры с решеткой цилиндров допустимо использовать существенно более простую модель.

Следует отметить, что система связанных ДВ рассматривалась во многих работах. В частности, в работе [14] для ее волн получено достаточно простое дисперсионное уравнение, которое легко может быть решено численно. Возможность использования простой приближенной модели существенно облегчает исследование рассмотренных структур, которые могут иметь практическое значение.

Литература

1. Банков С.Е. Дифракция электромагнитных волн на границе двух изотропных планарных волноводов // РЭ. 2013. Т. 58. № 10. С. 1002-1012.

2. M. Ettorre, S. Bruni, G. Gerini, A. Neto, N. Llombart, S. Maci, Multi Sector PCS-EBG Antenna for low cost high directivity applications, IEEE AP-S Symposium, Honolulu, Hawaii, June 2007.

3. Банков С.Е., Грачев Г.Г., Дупленкова М.Д., Фролова Е.В.. Проектирование и экспериментальное исследование интегральной зеркальной многолучевой антенны миллиметрового диапазона // РЭ. 2014. Т. 59. №6.

4. Скобелев С.П. Фазированные антенные решетки с секторными диаграммами направленности. М.: Физматлит. 2010.

5. Bankov S.E., Bugrova T.I. // Microwave and Optical Technology Letters, 1993. V. 6. P. 782.

6. Банков С.Е. Диаграммообразующая схема на неодинаковых связанных волноводах // РЭ. 2009. Т. 54. №7. С. 796-805.

7. Банков С.Е., Грачев Г.Г. Матричный облучатель на связанных диэлектрических волноводах // РЭ. 2014. Т. 59. №2. С. 132-142.

8. Банков С.Е., Грачев Г.Г., Дупленкова М.Д. Одномерные двухполяризационные диаграммообразующие схемы на связанных металлических волноводах // РЭ. 2012. Т. 57. №6. С. 613-623.

9. Унгер Г.Г. Оптическая связь. М.: Связь. 1979.

10. Банков С.Е., Курушин А.А., Гутцайт Э.М. Решение оптических и СВЧ задач с помощью HFSS. М.: Оркада, 2012.

11. Взятышев В.Ф. Диэлектрические волноводы. М.: Сов. Радио. 1970.

12. Банков С.Е., Пангонис Л.И. Экспериментальное исследование СВЧ волноводных элементов на основе EBG структур // РЭ. 2008. Т.53.№3. С. 295.

13. Воскресенский Д.И., Грановская Р.А., Давыдова Н.С. и др. Антенны и устройства СВЧ. М.: Радио и связь, 1981.

14. Банков С.Е., Клементьева А.В. Согласование решетки планарных диэлектрических волноводов // Журнал радиоэлектроники. 2013. №1. URL: http://jre.cplire.ru/jre/jan13/19/text.html.