ДЕЛИТЕЛЬ МОЩНОСТИ НА ОСНОВЕ EBG-ВОЛНОВОДА
В.А. Калошин, Л.И. Пангонис, Е.А. Скородумова
Институт радиотехники и электроники им. В.А. Котельникова РАН
Получена 1 апреля 2009 г.
Методом конечных элементов проведено численное моделирование и оптимизация конструкции Т-образного делителя мощности на основе EBG-волновода. Найдены параметры конструкции, обеспечивающие КСВ менее 1.2 в тридцати процентной полосе частот. Результаты математического моделирования подтверждены результатами физического эксперимента.
Ключевые слова: планарный EBG-волновод, численное моделирование в электродинамике, экспериментальная электродинамика.
Введение
В работе [1] проведено исследование ряда элементов на основе планарного EBG-волновода, выполненного в виде двумерно-периодической решетки из круговых металлических цилиндров. Рассматривался, в том числе, и делитель мощности на два канала. Однако предложенная конструкция делителя имеет большую длину, что затрудняет построение многоканальных делителей мощности. В данной работе с использованием метода конечных элементов строится математическая модель и проводится численное исследование и оптимизация Т-образного делителя мощности на основе EBG-волновода. Результаты численного моделирования для оптимальных параметров конструкции делителя, обеспечивающих минимальный КСВ, сопоставлены с результатами физического эксперимента в диапазоне 8–12 ГГц.
Описание математической модели
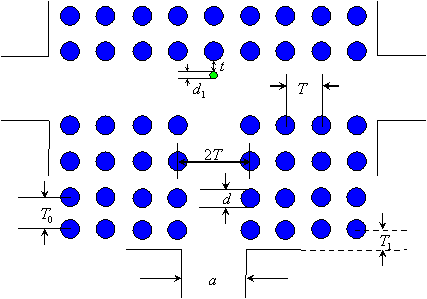
Рассмотрим отражение волны от делителя мощности, который представляет собой Т-образное сочленение волноводов, образованных удалением двух рядов металлических цилиндров с диаметром d = 5 мм в двумерной периодической решетке с периодом T = 12.5 мм (рис. 1). Вход и выходы делителя соединены с металлическими волноводами размером a = 23 мм с фланцами.
Согласование EBG-волновода с прямоугольным металлическим волноводом проводилось на основе результатов, полученных в работе [2] путем подбора расстояния между центрами цилиндров первого и второго ряда T0 и расстояния от центров цилиндров первого ряда до фланца металлического волновода T1.
Рис. 1
Для согласования Т-образного делителя мощности в области сочленения EBG-волноводов на расстоянии от ближайшего цилиндра решетки t располагался дополнительный цилиндр с диаметром d1.
Результаты численного исследования и оптимизации
Были проведены исследования зависимости КСВ на входе делителя мощности от частоты при различных значениях диаметра согласующего стержня d1 и расстояния t. Сначала подбиралось оптимальное расстояние t с точки зрения максимальной ширины полосы частот по уровню КСВ, равного 1.2. Наилучшие результаты были получены при значении t = 6.55 мм.
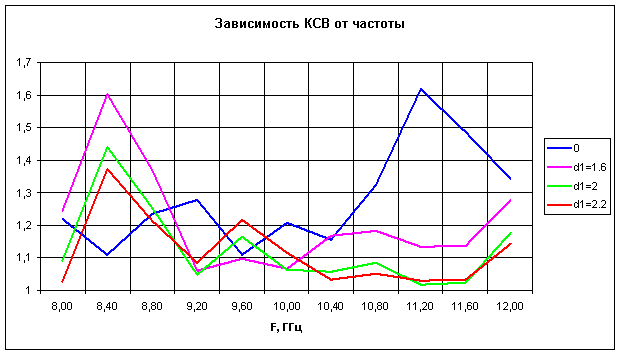
Рис. 2
Далее проводилось исследование влияния диаметра d1 согласующего стержня на КСВ. На рис. 2 приведены результаты расчетов КСВ в зависимости от частоты для трех различных величин d1 (1.6, 2 и 2.2 мм). Для сравнения на рисунке также приведены значения КСВ делителя мощности без согласующего элемента (синяя линия). Как видно из рисунка, оптимальное значение d1 = 2 мм. При этом КСВ не превышает уровень 1.2 в полосе частот от 9 до 12 ГГц. Следует отметить, что в данной конструкции величина КСВ связана не только с отражением от делителя мощности, но и от сочленений с металлическими волноводами на входе и выходах. Поэтому уровень КСВ собственно от делителя в рассмотренной полосе частот, очевидно, еще меньше.
Сравнение с экспериментом
Экспериментальный макет представлял собой две латунные пластины, между которыми располагались латунные втулки, соединенные с ними винтами. Вход и выходы делителя были соединены с прямоугольными волноводами сечением 23x10 мм. К выходным волноводам подключались согласованные нагрузки. Входной прямоугольный волновод был соединен с выходом панорамного измерителя КСВ Р2-61 (рис. 3).
Рис. 3. Экспериментальная установка
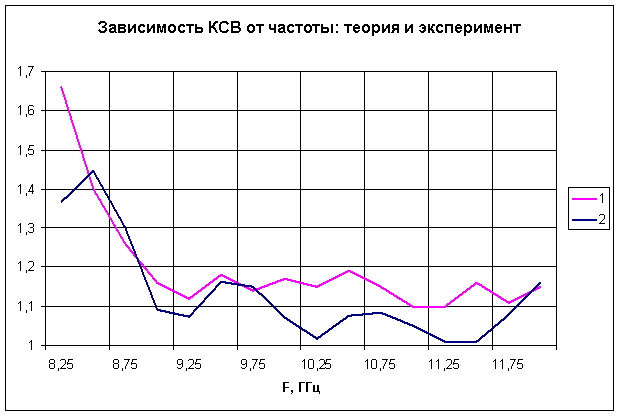
Результаты измерений приведены на рис. 4 (кривая 1). Для сравнения на этом же рисунке представлены результаты математического моделирования (кривая 2).
Рис. 4
Как видно из рисунка, результаты эксперимента в полосе частот 9–12 ГГц незначительно превышают значения КСВ, полученные на основе численного моделирования, что можно объяснить дополнительными отражениями от нагрузок.
Работа выполнена при поддержке РФФИ (проект №08-08-12200).
Литература
- S. E. Bankov, M.D. Duplenkova, Numerical analysis of waveguides and waveguide elements in EBG structures // JRE, 2006, №12 (http://jre.cplire.ru/jre/dec06/2/text.html).
- В.А. Калошин, Е.А. Скородумова, Возбуждение планарного EBG-волновода прямоугольным волноводом // ЖРЭ, 2009, №4