УДК 629.396.67
Синтез и анализ зеркально-линзовых диаграммо-образующих систем для планарных многолучевых антенн
В. А. Калошин, Е. В. Фролова
Институт радиотехники и электроники им. В.А. Котельникова РАН
Статья поступила в редакцию 10 декабря 2015 г.
Аннотация. Рассмотрена задача синтеза планарных двухслойных зеркально-линзовых сиcтем, преобразующих цилиндрический фронт в плоский. Получены дифференциальные уравнения для поверхностей систем зеркало-линза и линза-зеркало. В результате численного интегрирования дифференциальных уравнений для закона отображения, удовлетворяющего условию "синусов" Аббе, найдена форма поверхностей апланатических систем. Методом трассировки лучей при наклонном падении плоского фронта на одну из поверхностей (отражающую или преломляющую) проведен анализ несимметричных аберраций по критерию среднеквадратичной аберрации для пятна рассеяния при больших углах зрения. Проведено сравнение с аберрациями в двухслойных однозеркальных и трехслойных двухзеркальных планарных системах.
Ключевые слова: многолучевые антенны, зеркально-линзовые системы, аберрации, апланатические системы.
Abstract. The problem of synthesis of planar two- layer mirror-lens systems that convert a cylindrical front into a flat one is considered. Differential equations for the surfaces of the mirror-lens and lens-mirror systems are obtained. As a result of numerical integration of differential equations for the mapping of the law, satisfying the Abbe "sine" condition, forms of aplanatic system surfaces are found. Using ray tracing technique for a plane front oblique incidence on one of the surfaces (reflecting or refracting) the analysis of asymmetrical aberrations for a scattering spot is conducted for large angles of view with using mean square aberration criterion. A comparison with aberrations in a two-layer single-reflector and three-layer two-mirror planar systems is done.
Key words: multi-beam antenna, mirror-lens system, aberrations, aplanatic system.
Введение
В связи с развитием миллиметровых и субмиллиметровых широкополосных систем связи, радиолокации и радиовидения возрастает интерес к квазиоптическим схемам формирования многолучевых диаграмм направленности на основе планарных технологий [1-6]. Планарные квазиоптические фокусирующие системы можно реализовать на основе однослойных, двухслойных и трехслойных структур. В однослойных системах в качестве фокусирующих элементов используются линзы (Ротмана [1,2] и Люнебурга [3]) и несимметричные зеркальные системы [4]. Симметричные однозеркальные [5,6] и двухзеркальные [7] системы имеют, соответственно, двух и трехслойную конструкцию.
Недостатком однозеркальных систем с параболическим зеркалом и классических двухзеркальных систем (Грегори и Кассегрена) является наличие больших несимметричных аберраций, в первую очередь, “комы”, возникающих при больших углах отклонения лучей. Использование офсетных зеркальных систем приводит к дополнительному увеличению аберраций. Апланатическая двухзеркальная система Шварцшильда свободна от сферической аберрации и комы третьего порядка, а аберрации высших порядков могут быть минимизированы выбором параметров системы [7]. Однако преимущество симметричной апланатической системы реализуется в трехслойной структуре, что приводит к усложнению конструкции. С целью реализации симметричной апланатической системы на основе двухслойной конструкции в работе [8] предложены зеркально-линзовые системы, содержащие две поверхности, одна из которых – отражающая, а другая преломляющая.
1. Cинтез образующих зеркально-линзовых систем
Рассмотрим два варианта планарных двухслойных зеркально-линзовых систем, содержащих две поверхности, одна из которых – отражающая, а другая преломляющая. В первом варианте системы преломляющая поверхность вместе с облучателем располагается в первом слое. Этот тип системы будем называть зеркально-линзовая (ЗЛ) (первая буква в принятом обозначении обозначает тип поверхности, на которую падает плоская волна). Во втором варианте преломляющая поверхность находится во втором слое. Такую систему будем называть линзово-зеркальной (ЛЗ).

а) ЗЛ система б) ЛЗ система
Рис. 1. Двухслойные планарные зеркально-линзовые системы
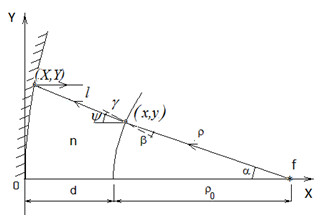
На рис. 2а, 2б показаны образующие
отражающих и преломляющих поверхностей, а также ход лучей в ЗЛ и ЛЗ системах,
соответственно. По аналогии с зеркальными системами будем называть первую
поверхность на пути лучей, выходящих из фокуса, – вспомогательной, вторую поверхность,
непосредственно формирующую плоский фронт, – главной. Пусть начало декартовой
системы координат 0X, 0Y находится в центре главной поверхности. Примем
следующие обозначения: f – фокальный отрезок, характеризующий положение
первичного фокуса на продольной оси системы 0X, d – расстояние между
образующими, ![]() – расстояние от фокуса до образующей
вспомогательной поверхности вдоль оси 0X, n - относительный показатель
преломления диэлектрика. Уравнение вспомогательной поверхности удобно описывать
радиус-вектором
– расстояние от фокуса до образующей
вспомогательной поверхности вдоль оси 0X, n - относительный показатель
преломления диэлектрика. Уравнение вспомогательной поверхности удобно описывать
радиус-вектором ![]() в полярной системе координат,
связанной с фокусом f. Обозначим
в полярной системе координат,
связанной с фокусом f. Обозначим ![]() угол
между нормалью к вспомогательной поверхности и падающим из фокуса лучом, l –
расстояние между двумя поверхностями вдоль луча,
угол
между нормалью к вспомогательной поверхности и падающим из фокуса лучом, l –
расстояние между двумя поверхностями вдоль луча, ![]() – угол
между лучом l и осью 0X. Декартовые координаты точки пересечения луча с
главной и вспомогательной поверхностью обозначим Y, X и y, x,
соответственно.
– угол
между лучом l и осью 0X. Декартовые координаты точки пересечения луча с
главной и вспомогательной поверхностью обозначим Y, X и y, x,
соответственно.
|
|
|
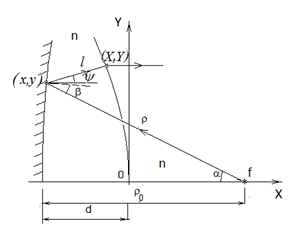
Рис. 2. Ход лучей в зеркально-линзовой и линзово-зеркальной системах.
Запишем систему равнений для схемы ЗЛ системы, изображенной на рис.2а. Условие равенства эйконала вдоль лучей:
Условия равенства проекций лучей на оси 0X и 0Z:
Условие “синусов” Аббе:
Соотношение между углами:
Закон преломления:
Дифференциальное уравнение радиус-вектора, описывающего вспомогательную поверхность, имеет вид:
Выразив S из (1) и подставив в (3), после подстановки (4) в (2) получим:
Откуда следует соотношение:
Преобразовывая (5) с учетом (6), получим выражение:
Дифференциальное уравнение (7) с
граничным условием ![]() примет вид:
примет вид:
где
Выражения для декартовых координат зеркал в соответствии со схемой на рис.2а имеют вид:
где
Для ЛЗ системы, которая изображена на рис. 2б, записав уравнения, аналогичные (1)-(7), и, выполнив такие же преобразования, получим следующие соотношения:
При этом в соответствии с рис.2б, выражения для декартовых координат поверхностей запишутся в виде:
Дифференциальные уравнения для образующей вспомогательной поверхности зеркально-линзовых, линзовых и зеркальных систем имеют общий вид (7) и отличаются лишь правой частью. Для апланатической двухзеркальной системы Шварцшильда функциональная зависимость для угла y определяется формулой:
Это дифференциальное уравнение для радиус-вектора образующей имеет аналитическое решение [9].
В случае двух преломляющих поверхностей (линзы) дифференциальное уравнение получено в [10], при этом соотношение для угла y имеет вид:
Дифференциальные уравнения
для зеркально-линзовых систем, как и для линзы, не имеют аналитического
решения, и решения могут быть получены только численно. Следует заметить, что
решение уравнений для зеркально-линзовых систем существует не для всех
значений параметров d, ![]() ,
, ![]() .
.
Примеры решений уравнения (12) для ЗЛ
системы, декартовые координаты образующих которой определяются соотношениями
(14), для произвольных параметров из области существования решений приведены на
рис.3: а) – d=0.16, ![]() =0.8,
=0.8, ![]() =1.2, n=4; б) – d=0.16,
=1.2, n=4; б) – d=0.16, ![]() =0.8,
=0.8, ![]() =0.97, n=1.48.
Здесь и далее все геометрические параметры нормированы на поперечный размер апертуры
главной поверхности (как было сказано ранее, поверхности, формирующей плоский
фронт в верхнем слое).
=0.97, n=1.48.
Здесь и далее все геометрические параметры нормированы на поперечный размер апертуры
главной поверхности (как было сказано ранее, поверхности, формирующей плоский
фронт в верхнем слое).

а) d=0.16, ![]() =0.8,
=0.8, ![]() =1.2, n=4
б) d=0.16,
=1.2, n=4
б) d=0.16, ![]() =0.8,
=0.8, ![]() =0.97,
n=1.48
=0.97,
n=1.48
Рис. 3. Примеры решения для образующих поверхностей ЗЛ систем.
На рис.4 приведены варианты
решений уравнения (17) для ЛЗ системы, декартовые координаты образующих которой
определяются соотношениями (19) для параметров: а) – d=0.2, ![]() =0.8,
=0.8, ![]() =0.88, n=1.6;
б) – d=0.2,
=0.88, n=1.6;
б) – d=0.2, ![]() =0.8,
=0.8, ![]() =0.7,
n=4.
=0.7,
n=4.

а) d=0.2, ![]() =0.8,
=0.8, ![]() =0.88, n=1.6
б) d=0.2,
=0.88, n=1.6
б) d=0.2, ![]() =0.8,
=0.8, ![]() =0.7,
n=4
=0.7,
n=4
Рис. 4. Примеры решения для образующих поверхностей ЛЗ систем.
На рис. 3,4 образующие показаны чёрным цветом, лучи, идущие от источника до пересечения с вспомогательной поверхностью – розовым, лучи плоского фронта – синим, а лучи, соединяющие точки на образующих отражающей и преломляющей поверхностей – голубым. Как видно на рисунках, варьированием параметров можно реализовать различные конфигурации зеркально-линзовых систем.
Следует добавить, что уравнения, приведённые выше, позволяют получить ещё два вида решений при замене величины относительного показателя преломления n на 1/n. В этом случае воздух и диэлектрик на схемах рис.1 следует поменять местами.
2. Анализ аберраций в зеркально-линзовых системах
Анализ аберраций в
зеркально-линзовых системах был проведён методом трассировки лучей в том его
варианте, когда рассматривается падение наклонного плоского фронта на главную
поверхность и исследуется пятно рассеяния в области фокусировки [7]. В качестве
характеристики уровня аберраций использовалась величина СКА (среднеквадратичной
аберрации), определённая в области фокусировки как среднеквадратичное отклонение
s точек пересечения пар зональных
лучей от главного луча (проходящего через центр главного зеркала). Эту величину
удобно использовать для анализа и минимизации несимметричных меридиональных аберраций,
преобладающих в планарных системах. Так же, как и в зеркальных системах, в
зеркально-линзовых системах СКА зависит от угла зрения w и трёх
геометрических параметров d, ![]() ,
, ![]() , дополнительным параметром является
показатель преломления диэлектрика n. Важная особенность аберраций в
апланатических системах – наличие минимума зависимостей СКА от фокального
радиуса при фиксированных параметрах d,
, дополнительным параметром является
показатель преломления диэлектрика n. Важная особенность аберраций в
апланатических системах – наличие минимума зависимостей СКА от фокального
радиуса при фиксированных параметрах d, ![]() [7].
Данную особенность можно использовать для эффективной оптимизации
зеркально-линзовых систем с целью минимизации аберраций и увеличения сектора обзора.
[7].
Данную особенность можно использовать для эффективной оптимизации
зеркально-линзовых систем с целью минимизации аберраций и увеличения сектора обзора.
В качестве примера анализа
аберраций рассмотрим ЗЛ систему с параметрами d=0.16, ![]() =0.8 и проанализируем характер зависимостей
СКА от фокального радиуса, рассчитанные для этой системы при изменении двух
параметров: угла зрения w (или угла наклона плоского фронта) и
показателя преломления n. Далее, как и в [7], будем описывать уровень
аберраций величиной
=0.8 и проанализируем характер зависимостей
СКА от фокального радиуса, рассчитанные для этой системы при изменении двух
параметров: угла зрения w (или угла наклона плоского фронта) и
показателя преломления n. Далее, как и в [7], будем описывать уровень
аберраций величиной ![]() , равной десятичному логарифму отношения
среднеквадратичной аберрации s к фокальному радиусу
, равной десятичному логарифму отношения
среднеквадратичной аберрации s к фокальному радиусу ![]() . Такая
нормировка позволяет непосредственно сравнивать угловые размеры
геометрооптического пятна рассеяния, определяемого аберрациями, и
дифракционного пятна, зависящего от электрического размера главной поверхности.
. Такая
нормировка позволяет непосредственно сравнивать угловые размеры
геометрооптического пятна рассеяния, определяемого аберрациями, и
дифракционного пятна, зависящего от электрического размера главной поверхности.
Результаты расчётов зависимостей
![]() от фокального радиуса
от фокального радиуса ![]() для фиксированного угла зрения w=20°
при изменении показателя преломления n в системе с приведёнными
параметрами представлены на рис. 5. Как видно на рисунке, с ростом показателя
преломления минимум уровня аберраций смещается в сторону больших значений
фокального радиуса
для фиксированного угла зрения w=20°
при изменении показателя преломления n в системе с приведёнными
параметрами представлены на рис. 5. Как видно на рисунке, с ростом показателя
преломления минимум уровня аберраций смещается в сторону больших значений
фокального радиуса ![]() , при этом величина аберраций в
минимуме уменьшается.
, при этом величина аберраций в
минимуме уменьшается.
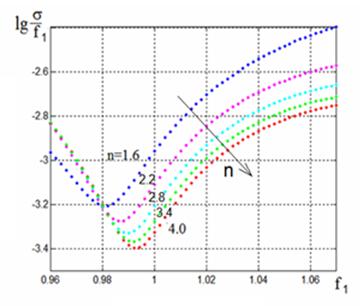
Рис. 5.
Зависимости уровня аберраций от фокального радиуса
для фиксированного угла
зрения w=20° при изменении показателя преломления.
На рис. 6 представлены
зависимости уровня аберраций ![]() в системе с теми же
параметрами d,
в системе с теми же
параметрами d, ![]() от фокального радиуса
от фокального радиуса ![]() для фиксированного значения n=4,
при этом переменным является угол зрения w. Как видно на рисунке, с
увеличением угла зрения, как и следовало ожидать, наблюдается рост уровня
аберраций, но при этом положение минимумов практически не меняется.
для фиксированного значения n=4,
при этом переменным является угол зрения w. Как видно на рисунке, с
увеличением угла зрения, как и следовало ожидать, наблюдается рост уровня
аберраций, но при этом положение минимумов практически не меняется.
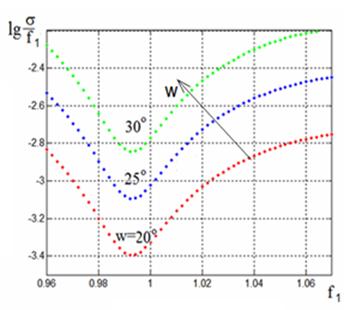
Рис. 6. Зависимости уровня аберраций
от фокального радиуса
для фиксированного показателя преломления n=4 при
изменении угла зрения w.
Дальнейший анализ аберраций
при варьировании параметров d, ![]() проведём
для двух вариантов ЗЛ систем. Назовём эти системы, отличающиеся между собой
относительными показателями преломления n и 1/n, соответственно,
ЗЛ1 и ЗЛ2. Отметим, что в системе ЗЛ1 в нижнем слое диэлектрик заполняет
область между преломляющей поверхностью и зеркалом, в системе ЗЛ2 – область от
фокуса до вспомогательной поверхности.
проведём
для двух вариантов ЗЛ систем. Назовём эти системы, отличающиеся между собой
относительными показателями преломления n и 1/n, соответственно,
ЗЛ1 и ЗЛ2. Отметим, что в системе ЗЛ1 в нижнем слое диэлектрик заполняет
область между преломляющей поверхностью и зеркалом, в системе ЗЛ2 – область от
фокуса до вспомогательной поверхности.
Рассмотрим характеристики
аберраций зеркально-линзовой системы ЗЛ1. Для выбранного значения показателя
преломления n=1.6 и заданного угла зрения w=20° после нахождения
для каждой пары параметров d, ![]() минимумов величины
минимумов величины ![]() и значений
и значений ![]() ,
соответствующих этим минимумам, были получены карты уровня минимальных
аберраций и соответствующих значений фокального радиуса в координатах d,
,
соответствующих этим минимумам, были получены карты уровня минимальных
аберраций и соответствующих значений фокального радиуса в координатах d,
![]() , изображённые на рис.7а, 7б,
соответственно.
, изображённые на рис.7а, 7б,
соответственно.
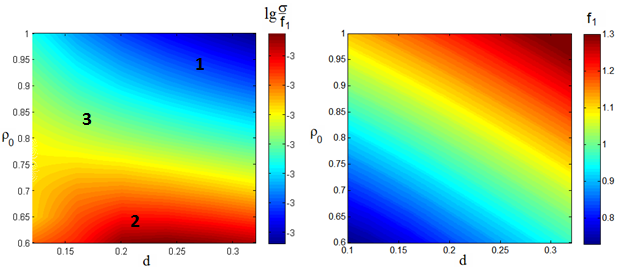
а) б)
Рис. 7. Уровень минимальных аберраций
(а) и соответствующие значения фокального радиуса (б)
в системе ЗЛ1 в
зависимости от параметров d,![]() .
.
Как видно на рисунке 7а, в
системах с оптимальным фокальным радиусом существуют области параметров d,![]() с минимальными (1) и с максимальными
аберрациями (2). Область (3) занимает промежуточное положение. Так же, как и в апланатических
двухзеркальных системах, с ростом габаритных параметров d,
с минимальными (1) и с максимальными
аберрациями (2). Область (3) занимает промежуточное положение. Так же, как и в апланатических
двухзеркальных системах, с ростом габаритных параметров d,![]() в области (1) уровень аберраций
уменьшается. Для наихудшей, с точки зрения уровня аберраций, области (3)
характерны малые значения
в области (1) уровень аберраций
уменьшается. Для наихудшей, с точки зрения уровня аберраций, области (3)
характерны малые значения ![]() <0.6. Представляет
интерес область с малыми расстояниями между поверхностями d<0.2. В
этой области при выборе величин
<0.6. Представляет
интерес область с малыми расстояниями между поверхностями d<0.2. В
этой области при выборе величин ![]() >0.7 можно получить
систему с относительно малыми аберрациями. Приведем результаты трассировки
наклонных лучей, иллюстрирующие аберрации в этих областях параметров. На рис.
8а-г приведены образующие поверхностей и ход лучей в системах с параметрами: a)
d=0.38,
>0.7 можно получить
систему с относительно малыми аберрациями. Приведем результаты трассировки
наклонных лучей, иллюстрирующие аберрации в этих областях параметров. На рис.
8а-г приведены образующие поверхностей и ход лучей в системах с параметрами: a)
d=0.38, ![]() =0.96,
=0.96, ![]() =1.36,
принадлежащими области (1), характеризующими системы с малыми аберрациями, но
при этом с большим продольным размером;
=1.36,
принадлежащими области (1), характеризующими системы с малыми аберрациями, но
при этом с большим продольным размером;
б) d=0.12, ![]() =0.88,
=0.88, ![]() =0.93, принадлежащими
левой верхней части области (3) ; в этой области уровень аберраций также
относительно мал;
=0.93, принадлежащими
левой верхней части области (3) ; в этой области уровень аберраций также
относительно мал;
в) d=0.2, ![]() =0.7, принадлежащими области (2) при неоптимальном
фокальном радиусе
=0.7, принадлежащими области (2) при неоптимальном
фокальном радиусе ![]() =1.07;
=1.07;
г) d=0.4, ![]() =0.65,
=0.65, ![]() =0.92, принадлежащими
области (3), характеризующейся значительными аберрациями.
=0.92, принадлежащими
области (3), характеризующейся значительными аберрациями.

а) d=0.38 ![]() =0.96
=0.96 ![]() =1.36 б) d=0.12
=1.36 б) d=0.12 ![]() =0.88
=0.88 ![]() =0. 93
=0. 93
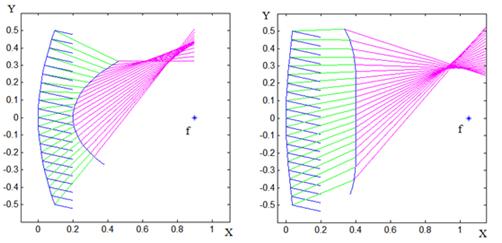
в) d=0.2 ![]() =0.7
=0.7 ![]() =1. 07 г) d=0.4
=1. 07 г) d=0.4 ![]() =0.65
=0.65 ![]() =0.92
=0.92
Рис. 8. Примеры трассировки лучей в зеркально-линзовых системах ЗЛ1.
Карты уровня минимальных
аберраций ![]() и соответствующих значений фокального
радиуса
и соответствующих значений фокального
радиуса ![]() в координатах d,
в координатах d, ![]() , полученные для зеркально-линзовой
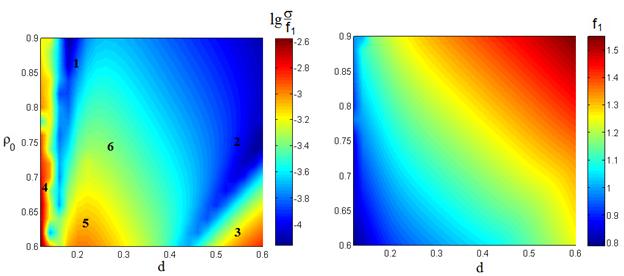
системы ЗЛ-2, изображены на рис.9а, 9б, соответственно для угла зрения w=20°.
Как и в предыдущем случае, показатель преломления диэлектрика n=1.6.
Как видно на рис.9а, в этой системе есть ярко выраженные две области с
минимальными аберрациями (1,2), области со значительными аберрациями (3,4,5) и
промежуточные области, например (6).
, полученные для зеркально-линзовой
системы ЗЛ-2, изображены на рис.9а, 9б, соответственно для угла зрения w=20°.
Как и в предыдущем случае, показатель преломления диэлектрика n=1.6.
Как видно на рис.9а, в этой системе есть ярко выраженные две области с
минимальными аберрациями (1,2), области со значительными аберрациями (3,4,5) и
промежуточные области, например (6).
а) б)
Рис. 9. Уровень минимальных аберраций
(а) и соответствующие значения фокального радиуса (б)
в системе ЗЛ2 в зависимости
от параметров d,![]() .
.
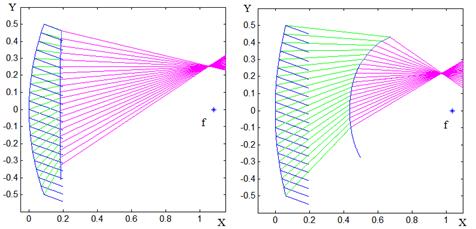
Рассмотрим результаты трассировки наклонных лучей, иллюстрирующие аберрации в этих областях параметров. На рис. 10а-г приведены образующие поверхностей и ход лучей в системах с параметрами:
а) d=0.18, ![]() =0.9,
=0.9, ![]() =1.19
из области (1), б) d=0.43,
=1.19
из области (1), б) d=0.43,![]() =0.6,
=0.6,![]() =1.07 из области (2). Эти системы характеризуются
малыми аберрациями.
=1.07 из области (2). Эти системы характеризуются
малыми аберрациями.
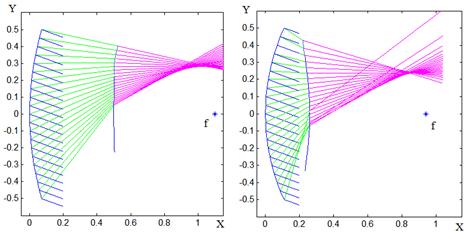
в) d=0.5 ![]() =0.6 из области (3) с неоптимальным
значением
=0.6 из области (3) с неоптимальным
значением![]() =1.4,
=1.4,
г) d=0.26 ![]() =0.68 из области (6) с неоптимальным
значением
=0.68 из области (6) с неоптимальным
значением ![]() =1.17.
=1.17.
Системы в), г) имеют высокий уровень аберраций, что мы видим, соответственно, по результатам трассировки на рис. 10в, г.
а) d=0.18 ![]() =0.9
=0.9 ![]() =1.19 б)
d=0.43
=1.19 б)
d=0.43 ![]() =0.6
=0.6 ![]() =1.07
=1.07
в) d=0.5 ![]() =0.6
=0.6 ![]() =1.4 г)
d=0.26
=1.4 г)
d=0.26 ![]() =0.68
=0.68 ![]() =1.17.
=1.17.
Рис. 10. Примеры трассировки лучей в зеркально-линзовых системах ЗЛ2.
Как следует из проведённых расчётов, в рассматриваемой области геометрических параметров зеркально-линзовых систем уровень аберраций может меняться более чем на порядок. Полученные данные об областях с минимальными аберрациями позволяют выбрать оптимальные параметры систем при заданной конфигурации и габаритах.
Подобное исследование можно
провести и для линзово-зеркальных систем. Ограничимся здесь лишь сравнительным анализом
различных систем с одинаковыми геометрическими параметрами d, ![]() и с одинаковым показателем преломления n.
Величины d,
и с одинаковым показателем преломления n.
Величины d, ![]() подбирались таким образом,
чтобы при этих параметрах существовали решения как для ЗЛ, так и для ЛЗ систем.
Расчеты были выполнены для d=0.16,
подбирались таким образом,
чтобы при этих параметрах существовали решения как для ЗЛ, так и для ЛЗ систем.
Расчеты были выполнены для d=0.16, ![]() =0.8,
значения фокального радиуса при этом изменялись в области существования решений.
Результаты расчетов зависимостей уровня аберраций
=0.8,
значения фокального радиуса при этом изменялись в области существования решений.
Результаты расчетов зависимостей уровня аберраций ![]() от
фокального радиуса
от
фокального радиуса ![]() для показателя преломления n=1.6
изображены на рис. 11. Кривые 1,2 на этом рисунке соответствует системам ЗЛ1, ЗЛ2,
кривые 3,4 – ЛЗ1, ЛЗ2, соответственно. Для сравнения на этом же рисунке
приведены зависимости, рассчитанные для двухзеркальной системы Шварцшильда (кривая
5), параболического зеркала (кривая 6) и зеркальной системы Кассегрена
(кривая 7) с эквивалентными параметрами. Для параболического зеркала вдоль оси
абсцисс отображено фокусное расстояние, для системы Кассегрена – эвивалентное
фокусное расстояние.
для показателя преломления n=1.6
изображены на рис. 11. Кривые 1,2 на этом рисунке соответствует системам ЗЛ1, ЗЛ2,
кривые 3,4 – ЛЗ1, ЛЗ2, соответственно. Для сравнения на этом же рисунке
приведены зависимости, рассчитанные для двухзеркальной системы Шварцшильда (кривая
5), параболического зеркала (кривая 6) и зеркальной системы Кассегрена
(кривая 7) с эквивалентными параметрами. Для параболического зеркала вдоль оси
абсцисс отображено фокусное расстояние, для системы Кассегрена – эвивалентное
фокусное расстояние.
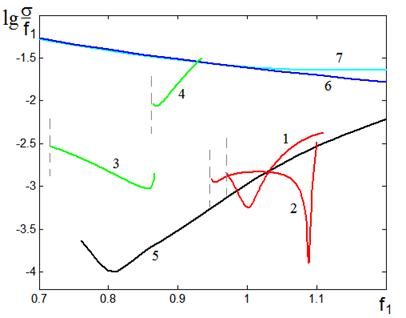
Рис. 11. Зависимость величины СКА от фокального радиуса (эквивалентного фокусного расстояния).
(Кривые 1-4 характеризуют
зеркально-линзовые системы:1– ЗЛ1, 2– ЗЛ2, 3 – ЛЗ1,4– ЛЗ2;
5 – апланат
Шварцшильда, 6 - параболическое зеркало, 7 – систему Кассегрена).
Как видно на рисунке, при одинаковых углах зрения в апланатических зеркально-линзовых системах (кривые 1-3) аберрации значительно меньше, чем в параболическом зеркале. При оптимальных параметрах в этих системах можно получить уровень аберраций, сравнимый с уровнем аберраций в двухзеркальной системе Шварцшильда.
Выводы
Планарные апланатические зеркально-линзовые системы при двухэтажной схеме могут обеспечить малые аберрации в широком угле зрения, что делает их перспективными при построении диаграммо-образующих схем планарных антенн и антенных решеток.
Работа выполнена при поддержке РФФИ, проект №15-07-07797.
Литература
1. Калошин В.А., Многолучевые гибридные антенны, Труды 13 Междун. Крымской конф. СВЧ техника и телекоммуникационные технологии, Crimico-2003, Севастополь, сентябрь 2003, с.383-390.
2. Cheng Н., Hong W., Wu K., Qi Kuai Z., Chen Yu, Chen J, Zhou J. and Tang H. Substrate Integrated Waveguide (SIW) Rotman Lens and Its Ka-Band Multibeam Array Antenna Applications // IEEE Trans. on Anten. and Prop., 2008, V.56, N 8. pp. 2504 - 2513.
3.Ахияров В.В., Калошин В.А., Никитин Е.А., Исследование широкополосных планарных линз Люнебурга // Журнал радиоэлектроники: электронный журнал. 2014, №1, http://jre.cplire.ru/jre/jan14/18/text.pdf.
4. Ettorre M., Neto A., Gerini G., Maci S. Leaky-Wave Slot Array Antenna Fed by a Dual Reflector System// Anten. and Prop., 2008, V.56, N10. pp.3143 - 3149.
5. Cheng Y., Hong W., and Wu K. Millimeter-Wave Substrate Integrated Waveguide Multibeam Antenna Based on the Parabolic Reflector Principle // IEEE Trans. on Anten. and Prop. 2008, V.56, N 9. pp. 3055 - 3058.
6. Gandini E., Ettorre M., Casaletti M., Tekkouk K., Le Coq L., Sauleau R.
SIW Slotted Waveguide Array with Pillbox Transition for Mechanical Beam Scanning // IEEE Anten. and Wireless Prop. Letters, 2012, V. 11. pp. 1572 - 1575.
7. Калошин В.А., Фролова Е.В. Анализ и минимизация аберраций в широкоугольных планарных зеркальных системах // Журнал радиоэлектроники: электронный журнал. 2014. N1. URL: http://jre.cplire.ru/jre/jan14/16/text.html.
8. Калошин В.А., Фролова Е.В. Синтез и анализ планарных зеркально-линзовых фокусирующих систем. II Всерос. Микроволновая конф. Доклады. М., ноябрь 2014. С. 461-467.
9. Галимов Г.К. Апланаты, т.3: “Антенны-связь НПК”, 2011.
10. Head A.K., Aplanatic Lens, Proc. of the Phys. Soc, 1959, Vol. 74, Issue 6, pp.731-736.
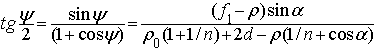
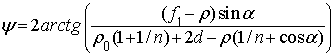 .
.
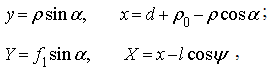 (14)
(14) 