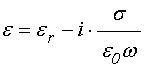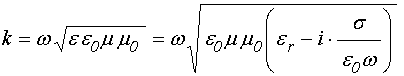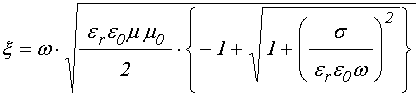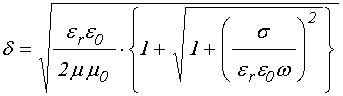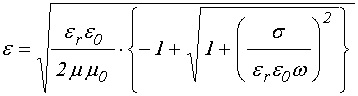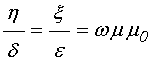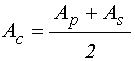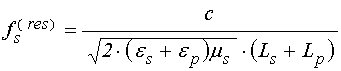Пространственное распределение амплитуд внешних и внутренних волн в ограниченной многослойной структуре с периодической неоднородностью. Часть 2. Электромагнитная волна.

УДК 537.874; 537.624

ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ АМПЛИТУД ВНЕШНИХ И ВНУТРЕННИХ ВОЛН В ОГРАНИЧЕННОЙ МНОГОСЛОЙНОЙ СТРУКТУРЕ С ПЕРИОДИЧЕСКОЙ НЕОДНОРОДНОСТЬЮ

ЧАСТЬ 2. ЭЛЕКТРОМАГНИТНАЯ ВОЛНА

И. В. Антонец¹, В. Г. Шавров², В. И. Щеглов²

¹Сыктывкарский государственный университет, Сыктывкар

²Институт радиотехники и электроники РАН, Москва

Статья получена 28 января 2015 г.

Аннотация. Методом пошагового алгоритма рассмотрено распространение электромагнитных волн прямого и обратного направлений в многослойной структуре ограниченной длины с периодической неоднородностью меандрового типа. Исследованы частотные зависимости амплитуд волн прямого и обратного направлений, а также трансформация частотных характеристик при изменении числа барьеров. Исследовано распределение амплитуд волн во внутренних слоях структуры, выявлены два главных вида распределения – синусоидальное и экспоненциальное. Для широкого диапазона частот введены определения сильной и слабой неоднородностей и получен критерий перехода между ними. Рассмотрена трансформация частотных зависимостей в широком интервале изменения соотношения проницаемостей слоев. Выявлено поджатие частотного спектра к своему нижнему концу при увеличении этого соотношения.

Ключевые слова: распространение волн, многослойная структура, периодическая неоднородность, частотный спектр.

Abstract. By successive steps algorithm method the electromagnetic waves of forward and backward directions propagation in multi-layer limited length structure with periodical nonuniformity of meander type is investigated. The frequency dependencies of forward and backward direction wave amplitudes and the transformation of frequency characteristics by barrier quantity variation are investigated. The amplitude wave distribution in inner layers of structure is investigated. It is found two main distributions: sinusoidal and exponential. For large frequency range it is introduced the definitions of strong and weak nonuniformities and the criterion of transition between its is found. The frequency dependencies transformation in large variation interval alignment of layer permittivity is investigated. It is found the compression of frequency spectrum to its lower limit when this alignment is increased.

Key words: wave propagation, multi-layer structure, periodical nonuniformity, frequency spectrum.

Введение

Интерес к распространению электромагнитных волн в периодических структурах имеет давнюю историю. Вслед за первыми работами в этой области, в значительной степени обобщенными в фундаментальных монографиях [1,2], последовало значительно количество работ, развивающих основные положения на различные виды волноведущих сред [3-6].

После открытия возможности создания композиционных сред из дискретных элементов [7,8], весьма перспективными для практических приложений стали считаться среды типа «фотонных кристаллов», позволяющие поддерживать не только прямые, но и обратные волны [9-14].

Другим параллельным направлением явилось исследование магнитных сред с периодически меняющимися свойствами, являющихся, по установившейся терминологии, «магнонными кристаллами» [15,16]. В первых подобных работах магнитная неоднородность создавалась за счет возбуждения в среде упругих волн, периодическим образом меняющих свойства среды за счет магнитострикции [17-19]. Важнейший цикл работ был посвящен исследованию магнитостатических волн в условиях периодического поля, создаваемого цепочкой внешних магнитов [20] или соответствующим образом намагниченной высококоэрцитивной магнитофонной лентой [21-25]. На основе таких структур была показана возможность не только создания эффективных фильтрующих устройств СВЧ диапазона [21-25], но и высокоточного измерения параметров магнитной анизотропии и намагниченности ферритовых пленок [26]. Наряду с изменением пространственно периодического магнитного поля, развивались работы по созданию «магнонных кристаллов» с помощью периодического изменения параметров самой магнитной среды, в том числе таких как толщина и намагниченность [27-29].

В большинстве перечисленных работ теоретическая трактовка наблюдаемых явлений базировалась, в первую очередь на моделях, основанных на применении теоремы Блоха, аппарата Хилла, Матье, Флоке и Кронига-Пенни, подробный обзор которых можно найти, например, в монографии [1]. Как уже отмечалось в первой части настоящей работы [30], общим недостатком таких теоретических моделей является невозможность исследования распределения возбуждений в отдельных слоях структуры. Для преодоления такого недостатка в [30], использован метод пошагового алгоритма [31-36], с помощью которого на примере одномерной волны рассмотрено распространение волн прямого и обратного направлений в структуре ограниченной длины с периодической неоднородностью типа симметричного меандра. Исследованы амплитуды волн прямого и обратного направлений при изменении координаты, номера слоя структуры и среднего волнового числа, выявлен эффект «вторичной модуляции». Рассмотрено распределение амплитуд при значительном соотношении между волновыми числами сред, составляющих структуру. Обнаружена пространственная модуляция амплитуды, представленная пятью основными режимами. Для объяснения особенностей наблюдаемых явлений предложена аналогия с цепочкой последовательно соединенных резонаторов.

Настоящая вторая часть работы посвящена обобщению полученных результатов на случай электромагнитных волн.

1. Геометрия задачи

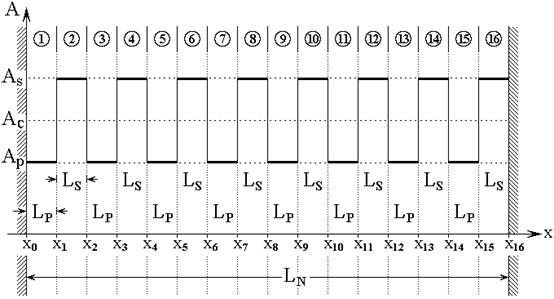
Геометрия задачи, полностью совпадающая с приведенной в первой части настоящей работы [30], показана на рис.1. Рассматривается симметричная меандровая структура, то есть такая, в которой неоднородность представляет собой периодически расположенные одинаковые прямоугольные барьеры, с одинаковыми промежутками между ними.

Рис.1. Общая схема ограниченной многослойной структуры с периодической неоднородностью симметричного меандрового вида.

Цифры в кругах – номера слоев (сред).

Структура содержит два вида сред, обозначаемых далее индексами «» и «», каждый из которых имеет собственные значения диэлектрических , и магнитных , проницаемостей, а также проводимостей , . Отложенные по вертикальной оси обозначения соответствуют адмиттансам сред и поясняются далее. Остальные обозначения подобны приведенными в [30] и ясны из рисунка (некоторые буквы по сравнению с [30] изменены, что сделано для удобства дальнейшего изложения).

2. Обобщение на случай электромагнитных волн

В работе [30] рассмотрение проведено на основе волнового числа, которое для одномерной волны является определяющим параметром. Для электромагнитной волны с прикладной стороны более важным параметром является частота, поэтому проведем дальнейшее рассмотрение опираясь именно на частоту падающей волны. Для перехода от одномерной волны к электромагнитной воспользуемся правилами эквивалентности, приведенными в работах [37-39].

В настоящем рассмотрении для простоты ограничимся случаем нормального падения волны, не требующим учета сложных угловых соотношений. Будем полагать, что все среды однородны и изотропны, то есть диэлектрическая и магнитная проницаемости, а также проводимость везде являются постоянными скалярными величинами.

Согласно [37-39], при этом достаточно во всех выражениях, полученных для одномерной волны, кроме показателей экспонент, заменить волновые числа величинами, обратными соответствующим импедансам:

, (1)

где:

, (2)

причем и – магнитная и диэлектрическая проницаемости -го слоя, и – магнитная и электрическая постоянные системы СИ.

Как можно видеть из работы [30], при методе пошагового алгоритма все выражения получаются в виде линейных комбинаций из волновых чисел. При замене (1) такие выражения будут содержать суммы дробей с различающимися знаменателями, поэтому, чтобы избежать необходимости их суммирования, удобно импедансы слоев заменить на обратные им величины – адмиттансы:

. (3)

В этом случае замена (1) существенно упрощается и принимает вид:

. (4)

При этом волновые числа в показателях экспонент остаются прежними:

, (5)

где – частота, задаваемая падающей волной в первом или последнем слое.

В случае электромагнитных волн вместо одномерных амплитуд и присутствуют амплитуды электрического и магнитного полей и . Однако, как следует из классики [40,41], а также для рассматриваемой геометрии подробно показано в [37-39], магнитное поле волны в каждом слое может быть представлено как производная по времени от электрического поля в том же слое, поэтому достаточно рассмотреть только амплитуды какого-то одного поля, например электрического.

Чтобы различать волны прямого и обратного направлений, будем электрические поля таких волн снабжать индексами: для прямого направления – индексом «», для обратного – «», после которых будем приводить номер слоя.

Как и в работе [30], будем полагать, что отражение волн при координатах и отсутствует, причем в среде №1 распространяется в положительном направлении волна с амплитудой , а в середе №16 – в отрицательном направлении волна с амплитудой , обе из которых по отношению к структуре в целом являются падающими.

Для упрощения записи экспонент при введем обозначения:

, (6)

а также:

, (7)

где – начальная фаза, которую без особенного ограничения общности можно положить равной нулю.

3. Случай проводящей среды

Если среда обладает проводящими свойствами, то в этом случае для нее наряду с основными параметрами, такими как диэлектрическая и магнитная проницаемости и , важнейшее значение приобретает проводимость .

Рассмотрим, как выражаются приведенные замены (4)-(5) через эти параметры. Для простоты дальнейшей записи соответствующий номеру среды индекс «» будем опускать.

При записи уравнений электродинамики для проводящей среды ее проводимость удобно включить в диэлектрическую проницаемость в виде мнимой добавки [42-44]:

, (8)

где – действительная часть волнового числа.

При этом полное волновое число, становясь комплексным, приобретает вид:

. (9)

Преобразуя эту формулу по правилам извлечения квадратного корня из комплексного числа [45], получаем:

, (10)

где:

; (11)

. (12)

Именно в таком виде волновое число будет входить в показатель экспоненты.

Рассмотрим теперь, как преобразуется адмиттанс в среде с проводимостью, для чего подставим (8) в (3).

В результате получаем:

, (13)

где:

; (14)

. (15)

В таком виде адмиттансы будут входить в линейные суммы выражений, получающихся в ходе реализации пошагового алгоритма.

Из приведенных формул можно видеть, что действительные и мнимые части волнового числа и адмиттанса связаны соотношениями:

. (16)

4. Особенности геометрии задачи для случая электромагнитных волн

Следуя общим правилам, сформулированным в предыдущем разделе, внесем некоторую коррекцию в геометрию данной задачи по сравнению со случаем одномерной волны. В одномерном случае полагалось, что структура содержит два вида сред с волновыми числами и , причем:

. (17)

Переходя на адмиттансы в соответствии с (4), получаем:

. (18)

Аналогично [30] можно ввести среднее значение адмиттанса:

, (19)

а также добавки к нему , такую, что:

; (20)

. (21)

Замечание. В соответствии с (5), из (17) получаем:

. (22)

С другой стороны, из (18), в соответствии с (3), получаем:

. (23)

При , что имеет место в большинстве немагнитных сред, особенно в оптическом диапазоне, соотношения (22) и (23) совпадают друг с другом, однако при произвольных значениях и они могут различаться, в результате чего соотношение (23) может быть обратным, то есть и на рис.1 надо поменять местами. Такое обстоятельство необходимо учитывать в случае магнитных сред, особенно на частотах, соответствующих ферромагнитному резонансу в одной из групп слоев, где магнитная проницаемость может возрасти на несколько порядков [46]. Данный случай выходит за рамки настоящей работы и требует более подробного рассмотрения. Здесь же ограничимся случаем (22) и будем далее с позиций многобарьерной структуры [30] рассматривать как величину адмиттанса, соответствующую промежуткам между барьерами, а за величину адмиттанса, соответствующую барьерам, примем .

5. Схема расчета методом пошагового алгоритма

Для расчета амплитуд в слоях многослойной структуры, как и в случае одномерной задачи [30], будем пользоваться методом пошагового алгоритма [31-36], позволяющим получить значения амплитуд во всех слоях. Приведем сначала общую схему метода, после чего дадим ее аналитическую реализацию.

6. Общая схема пошагового алгоритма

Общая схема пошагового алгоритма аналогична таковой для одномерной волны [30]. Алгоритм содержит два этапа, состоящих в последовательном прохождении по слоям структуры от одного конца структуры к другому и обратно.

На первом этапе сначала с помощью простых правил задаются вспомогательные величины, определяемые параметрами первого слоя. Из них на основе параметров первого и второго слоев формируются новые величины, принадлежащие второму слою. Затем таким же образом из величин второго слоя формируются величины третьего слоя и так далее до тех пор, пока все слои структуры не будут исчерпаны. Формирование последующих величин из предыдущих производится путем увеличения порядковых индексов всех предыдущих величин на единицу. Второй этап начинается с формирования вспомогательных величин, определяемых параметрами последнего слоя структуры. Далее из этих величин с использованием параметров последнего и предпоследнего слоев формируются подобные величины для предпоследнего слоя и так далее. Процедура формирования последующих величин из предыдущих состоит в уменьшении порядковых индексов всех предыдущих величин на единицу.

Из всех величин, получаемых на обоих этапах, с помощью простых правил суммирования формируются детерминанты, определяющие амплитуды волн внутри слоев.

7. Аналитическая реализация алгоритма

Аналитическая реализация пошагового алгоритма для электромагнитной волны подобна таковой для одномерной волны с учетом замен, приведенных в предыдущих разделах. Изложим далее ее в последовательном виде.

Этап №1.

Вводим вспомогательное обозначение:

, (24)

а также полагаем начальную тройку основных обозначений:

; (25)

; (26)

. (27)

С использованием (25)-(27) формируем новую тройку выражений:

; (28)

; (29)

. (30)

Далее, увеличивая порядковые номера индексов на единицу, получаем следующую тройку подобных выражений и так далее, вплоть до , , . Общие формулы для получения последующих выражений из предыдущих при произвольном номере имеют вид:

, (31)

, (32)

. (33)

Процесс заканчивается при достижении значения . При этом получаем:

; (34)

; (35)

. (36)

Этап №2.

Введем другое вспомогательное обозначение:

, (37)

а также положим другую начальную тройку основных обозначений, индексы которых зададим равными полному количеству слоев:

; (38)

; (39)

. (40)

С использованием (38)-(40) формируем тройку выражений:

; (41)

; (42)

. (43)

Далее, уменьшая порядковые номера индексов на единицу, получаем следующую тройку подобных выражений и так далее, вплоть до , , . Общие формулы для получения последующих выражений из предыдущих при произвольном номере имеют вид:

; (44)

; (45)

. (46)

Процесс заканчивается при достижении значения . При этом получаем:

; (47)

; (48)

. (49)

Формирование детерминантов.

Из полученных выражений формируем детерминанты следующим образом:

; (50)

; (51)

; (52)

; (53)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

; (54)

; (55)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

; (56)

. (57)

Здесь индексы детерминантов соответствуют номерам слоев, а выражения (50) и (57), определяющие , имея различный вид записи, тождественно равны.

Найденные детерминанты (50)-(57) позволяют определить амплитуды всех волн через и с помощью формул, задающих амплитуды волн в точках их исхода:

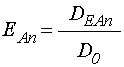; . (58)

При этом амплитуда волны, выходящей из структуры в положительном направлении оси , в точке равна:

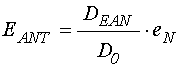; (59)

а амплитуда волны, выходящей в отрицательном направлении оси , в точке равна:

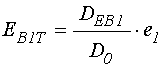. (60)

Описанный здесь метод будет далее применен для численного расчета амплитуд волн прямого и обратного направлений в структуре, схема которой показана на рис.1. Перейдем к описанию результатов расчетов.

8. Амплитуды волн в крайних слоях структуры

Рассмотрим сначала амплитуды волн в крайних слоях структуры при изменении частоты. Структура содержит 16 слоев, из которых 7 являются барьерами с диэлектрической проницаемостью выше, чем у промежутков. Барьерами являются слои с четными номерами от №2 до №14, промежутками – с нечетными от №1 до №15, последний слой №16 имеет те же параметры, что и №15, то есть параметры промежутка. Это сделано для того, чтобы параметры обеих внешних сред были одинаковыми. Полная длина структуры , толщина одного слоя . На структуру падает одна волна прямого направления с амплитудой (при этом ). На настоящем этапе рассматривается интервал изменения частоты падающей волны от до .

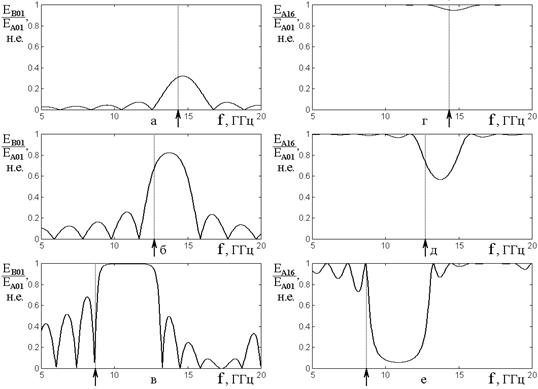
На рис.2 показаны зависимости нормированных амплитуд волн обратного (а, б, в) и прямого (г, д, е) направлений в крайних слоях структуры от частоты падающей волны. По горизонтальным рядам рисунка увеличивается диэлектрическая проницаемость барьера: в первом ряду (а, г) она равна , что мало отличается от проницаемости промежутка , во втором ряду (б, д) – , что отличается несколько больше, в третьем ряду (в, е) – , что превышает проницаемость промежутка в три раза.

Рис.2. Зависимости нормированных амплитуд волн в крайних слоях структуры от частоты падающей волны. а, б, в – волна обратного направления в слое №1. г, д, е – волна прямого направления в слое №16.

Параметры материала сред:; ; ;

а, г – ; б, д – ; в, е – .

Из рисунка видно, что с увеличением различия между диэлектрическими проницаемостями барьера и промежутка амплитуды волн обоих направлений возрастают, причем это возрастание для волн обратного направления (а, б, в) выражено сильнее, чем для волн прямого (г, д, е). Зависимости для амплитуд волн прямого направления (г, д, е) симметричны относительно горизонтальной оси зависимостям для амплитуд волн обратного направления (а, б, в) с тем отличием, что для них амплитуда несколько меньше, причем это различие с увеличением проницаемости уменьшается. Так при различие составляет около пяти раз, при – около двух раз, при амплитуда волн прямого направления уже приближается к амплитуде волн обратного направления и составляет от нее около .

Общий вид тех и других зависимостей представляет собой большой центральный лепесток, по обе стороны от которого располагаются лепестки-сателлиты, амплитуда которых по мере удаления от центрального лепестка спадает. Ширина сателлитов меньше ширины центрального лепестка тем более, чем различие проницаемостей выше. Так при сателлиты уже центрального лепестка примерно в два раза, тогда как при различие ширины достигает уже пяти раз.

Как и в работе [30], многолепестковый характер обеих зависимостей обусловлен интерференционными явлениями при многократном переотражении волн обоих направлений. Заметим, что, по сравнению с работой [30, рис.2], многолепестковый характер амплитуды здесь выражен сильнее, чем для рассмотренной там одномерной волны, что, по-видимому, обусловлено тем что там менялось только одно волновое число барьера , тогда как волновое число промежутка оставалось неизменным, здесь же при изменении частоты меняются оба волновых числа и , в соответствии с формулой (5).

Совокупность расположенных друг за другом барьеров представляет собой цепочку одинаковых последовательно соединенных через промежутки полуволновых резонаторов. Для каждого из таких резонаторов собственная длина волны связана с длиной барьера соотношением:

, (61)

то есть резонансная частота имеет вид:

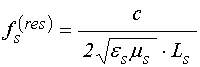, (62)

где – скорость электромагнитной волны в свободном пространстве ().

Подставляя в эту формулу получаем частоту , подставляя , получаем , подставляя , получаем . На соответствующих эпюрах эти значения частот показаны стрелками на горизонтальной оси и вертикальными точечными линиями.

Видно, что расчетные значения частот всегда лежат несколько ниже положения максимумов главного лепестка, причем это рассогласование с увеличением возрастает. Так для оно не превышает от частоты максимума, для составляет около , а для достигает . В этом последнем случае расчетное значение частоты приходится как раз на низший по частоте край главного лепестка.

Дополнительное исследование показывает, что если теперь зафиксировать значение диэлектрической проницаемости барьера на достаточно высоком уровне и повышать значение диэлектрической проницаемости промежутка , приближая ее к проницаемости барьера, то центральная частота главного лепестка понижается, стремясь к резонансной частоте барьера. Так при и максимум главного лепестка приходится на , что уже весьма близко к резонансной частоте для барьера, равной . Амплитуда максимума при этом также резко снижается, для отражения составляя , а для прохождения – около

Таким образом, частота главного лепестка, хотя и определяется в первую очередь диэлектрической проницаемостью барьера, но отклоняется от резонансной частоты барьера вниз тем сильнее, чем больше различие диэлектрических проницаемостей барьера и промежутка.

9. Изменение числа барьеров

Согласно принятой постановке задачи, структура содержит конечное число одинаковых барьеров, разделенных одинаковыми промежутками, геометрическая длина которых равна геометрической длине барьеров. Рассмотрим сначала, как меняются частотные свойства структуры в зависимости от полного числа составляющих структуру барьеров. Будем полагать, что различие параметров барьеров и промежутков недостаточно для приближения коэффициентов отражения и прохождения структуры в целом к единице (то есть тот или другой коэффициент составляет не более ).

Рис.3. Зависимость нормированной амплитуды волны обратного направления в слое №1 от частоты при различном количестве барьеров: а – 1; б – 2; в – 3; г – 4; д – 7. Шаг по частоте – . Параметры материала сред:

; ; ; .

Частотные свойства такой структуры иллюстрируются рис.3, где показаны зависимости нормированной амплитуды волны обратного направления в слое №1 от частоты при различном количестве барьеров. Волна падает на структуру только из слоя №1, то есть отлично от нуля, тогда как .

Наблюдаемая ситуация соответствует частотной зависимости коэффициента отражения (по амплитуде). Поскольку , то затухание волны отсутствует, то есть коэффициент поглощения равен нулю, а частотная зависимость коэффициент прохождения аналогична таковой для коэффициента отражения с точностью до обратного знака по амплитуде (подобно описанному в работе [37-39,47,48]), поэтому на данном этапе не рассматривается.

10. Минимальные значения амплитуды

Из рисунка видно, что частотные зависимости имеют вид многолепесткового повторения кривых, похожих на положительный полупериод синусоиды, причем по мере увеличения числа барьеров количество лепестков увеличивается.

При единственном барьере (рис.3а) зависимость имеет вид периодически повторяющейся четкой половины синусоиды. При заданных параметрах материала барьера длина волны в его пределах равна . Учитывая, что длина барьера равна , можно видеть, что в этом случае на длине барьера укладывается как раз половина длины волны. Таким образом, минимум отражения здесь соответствует хорошо известному в оптике свойству полуволновой пластинки, вытекающего из потери полуволны при отражении от менее плотной среды [49,50]. Частотные положения следующих друг за другом минимумов отражения определяются формулой:

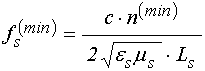, (63)

где – порядковый номер минимума, показывающий, сколько полуволн укладывается по длине барьера, – скорость электромагнитной волны в свободном пространстве ().

При , и первый минимум соответствует частоте , второй – , третий – и так далее. Положения первых двух минимумов отмечены на рисунке стрелками, подходящими снизу к горизонтальной оси.

При увеличении числа барьеров (рис.3б-3д) положения по частоте этих основных минимумов сохраняются (отмечены стрелками), однако появляются новые дополнительные минимумы, частоты которых уже в простые соотношения не укладываются и требуют более подробного рассмотрения условий интерференции. Не вдаваясь в такое рассмотрение, отметим здесь лишь наиболее явные особенности наблюдаемой картины.

Так при двух барьерах (рис.3б) кроме основных появляются минимумы при (в ГГц): , , , , то есть ниже первого основного () – два дополнительных ( и ), между первым и вторым основными ( и ) – один дополнительный () и выше в пределах шкалы рисунка еще один дополнительный (). При трех барьерах (рис.3в) ниже первого основного появляются четыре дополнительных, между основными – три и выше еще один. При четырех (рис.3г) ниже первого – пять, между основными – пять. При семи барьерах (рис.3д) ниже первого – десять, между основными – девять.

Таким образом, при увеличении числа барьеров количество минимумов всегда возрастает, как ниже первого минимума, так и между двумя основными. При этом при увеличении числа барьеров от двух до четырех количество минимумов между основными подчиняется соотношению:

, (64)

где – число барьеров. Однако это соотношение нельзя считать безупречным. Так, можно было бы ожидать, что при количество минимумов между основными должно равняться одиннадцати, однако из рис.3д видно, что в этом интервале минимумов всего девять. Более точная проверка с шагом по частоте в () показала, что на рисунке минимумы при и не разрешены из-за их чрезвычайной близости. Однако между основными было обнаружено не одиннадцать, а всего десять минимумов, то есть опять-таки на единицу меньше приведенного соотношения. Возможной причиной нарушения соотношения (64) при увеличении числа барьеров может явиться возрастание сложности интерференционной картины при многочисленных переотражениях волн внутри структуры.

11. Максимальные значения амплитуды

Обратимся теперь к рассмотрению главных максимумов приведенных зависимостей, имеющих наибольшую амплитуду.

При единственном барьере (рис.3а) зависимость амплитуды от частоты в рассматриваемом интервале частот имеет два максимума – при частотах и , которые соответствуют укладыванию по длине барьера нечетного числа четвертей длины волны. Частотные положения следующих друг за другом максимумов отражения определяются формулой:

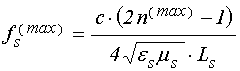, (65)

где – порядковый номер максимума, при котором на длине барьера укладывается четвертей длин волн, – скорость электромагнитной волны в свободном пространстве (). Таким образом, максимум отражения здесь также соответствует известному в оптике свойству четвертьволновой пластинки [49,50]. При большем числе барьеров картина максимумов, как и минимумов, также не поддается столь простому расчету, поэтому отметим лишь ее основные особенности.

При увеличении числа барьеров положения по частоте наблюдаемых на рис.3а максимумов смещаются несколько вверх, при двух барьерах (рис.3б) принимая значения и , а при семи барьерах (рис.3д) – и соответственно. Однако, начиная с двух барьеров (рис.3б), между ними появляется еще один дополнительный максимум при , который при увеличении числа барьеров смещается не вверх, а вниз, выходя при семи барьерах (рис.3д) на частоту .

При такой трансформации соответствующие максимумам лепестки значительно сужаются. Так по расстоянию между двумя ближайшими минимумами ширина обоих лепестков при одном барьере составляет . При двух барьерах ширина основных лепестков составляет: нижнего по частоте – , верхнего – , а ширина лепестка между ними – . При семи барьерах эти же величины уменьшаются до , и соответственно.

Амплитуды всех максимумов при увеличении числа барьеров возрастают. Так при одном барьере амплитуды обоих основных максимумов равны , при двух барьерах амплитуда низшего по частоте максимума составляет , а высшего – Амплитуда находящегося между ними дополнительного максимума равняется При семи барьерах эти же величины соответственно равны , и То есть дополнительный максимум сужается быстрее, но по амплитуде растет несколько медленнее основных.

12. Распределение амплитуд в слоях при большой вариации параметров

Рассмотрим распределение амплитуд в слоях при большом изменении параметров материала от слоя к слою. Ограничимся рассмотрением волн прямого направления, так как характер распределения волн обратного направления аналогичен подобно таковому в работе [30].

Замечание. В работе [30] приведенные далее зависимости амплитуд волн в слоях от координаты по длине структуры, полученные для одномерной волны, названы «режимами». Однако, как показано там же, резких границ между такими «режимами» нет, причем принципиально отличаются друг от друга только два: №1 и №4 – синусоидальный и экспоненциальный. Поэтому в настоящей работе мы предпочли отказаться от наименования «режимы» и заменить их на наш взгляд более естественным названием «распределения», которое и будет использоваться далее.

На рис.4 показаны распределения нормированных амплитуд волн прямого направления в слоях от координаты при различных частотах падающей волны. Эпюры расставлены по частоте и сгруппированы по столбцам в соответствии с характерными частотными областями распределений. Утолщенные горизонтальные линии – амплитуды волн прямого направления в соответствующих слоях. Укрупненные точки соответствуют серединам перепадов амплитуд между соседствующими слоями. Утолщенные сплошные кривые построены по эмпирическим формулам синусоиды, прямой или экспоненты, подобным приведенным в работе [30].

Из рисунка можно видеть, что здесь в случае электромагнитной волны присутствуют те же основные виды распределения амплитуд, что и в случае одномерной. Главными видами являются синусоидальное и экспоненциальное. Эти виды распределения при изменении частоты чередуются друг за другом, а переход между ними происходит через посредство полусинусоидального и линейного распределения.

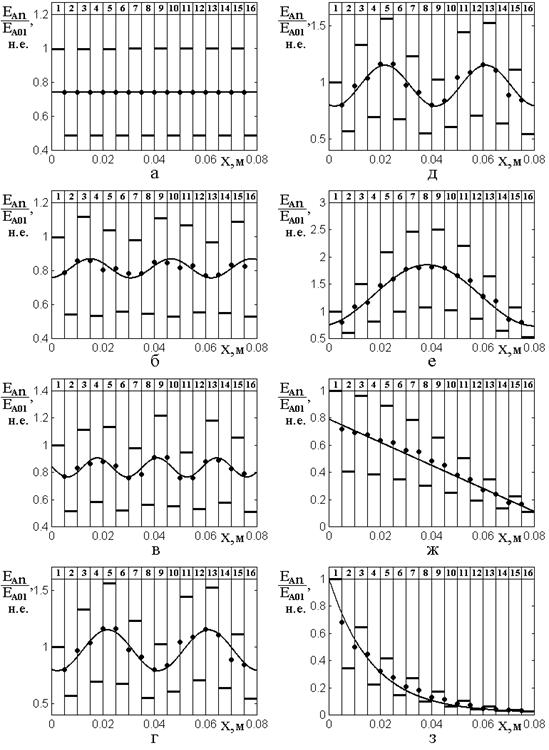
Рис.4. Распределение нормированных амплитуд волн прямого направления в слоях от координаты при различных частотах падающей волны.

Цифры в верхнем ряду – номера слоев. Параметры материала слоев:

; ; ; . Частоты следующие:

а – ; б – ; в – ; г – ;

д – ; е – ; ж – ; з – .

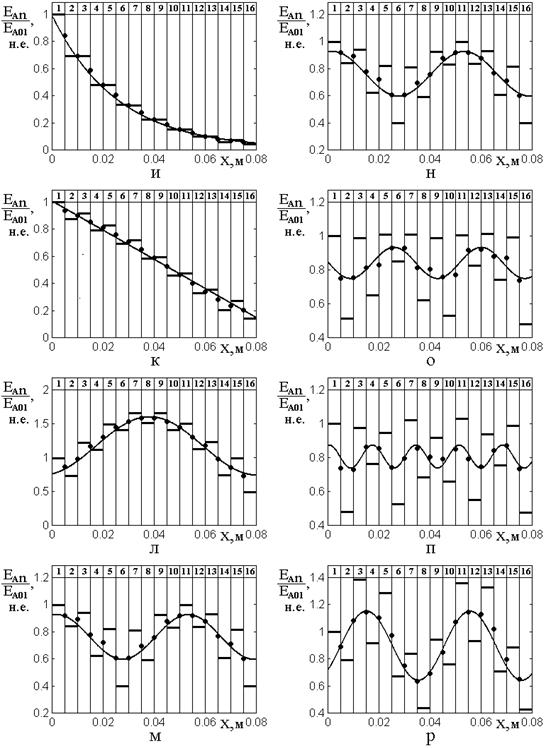
Рис.4 (продолжение). Частоты следующие:

и – ; к – ; л – ; м – ;

н – ; о – ; п – ; р – .

Если за точку перехода от синуса к экспоненте считать прямую линию, то переходы соответствуют частотам (рис.4ж) и (рис.4к). Следующие точки подобного перехода соответствуют частотам , и так далее с интервалами по .

На частотах ниже зависимость распределения амплитуд от координаты практически отсутствует, причем это отсутствие выражено тем сильнее, чем частота ниже, так что для частоты изменение амплитуды в слоях составляет менее (рис.4а). При увеличении частоты заметно выше распределение постепенно приобретает синусоидальный характер и при частоте (рис.4б) изменение амплитуды достигает уже .

Распределение амплитуд в интервале от (рис.4б) до (рис.4д) носит типичный синусоидальный характер. На рисунке полной эволюции распределения амплитуд от отсутствия распределения до конца синусоидального соответствует первый столбец от 4а до 4г. Считая от нуля, ширина полного интервала по частоте здесь составляет около

Однако при дальнейшем увеличении частоты всего на то есть уже на частоте синусоидальное распределение сменяется полусинусоидальным (рис.4е), которое при дальнейшем увеличении частоты на до переходит в линейное (рис.4ж), а затем при увеличении еще на до – в экспоненциальное (рис.4з). Таким образом, полный интервал смены синусоидального распределения на экспоненциальное заключен между и , чему на рисунке соответствует второй столбец (от 4д до 4з), причем этот интервал составляет не более .

Далее вплоть до частоты распределение является экспоненциальным (рис.4и). Полный интервал экспоненциального распределения составляет не менее .

При увеличении частоты с до экспоненциальное распределение переходит в линейное (рис.4к), затем при частоте – в полусинусоидальное (рис.4л), после чего, начиная с частоты , в синусоидальное (4м). Эта трансформация представлена третьим столбцом рисунка. Интервал здесь составляет .

Далее синусоидальное распределение, претерпевая некоторые вариации периода, как это показано на рис.4о – рис.4р (четвертый столбец рисунка), остается таковым вплоть до (на рисунке дальнейшие эволюции не показаны), где сменяется полусинусоидальным, затем на частоте – линейным, которое на частоте переходит в экспоненциальное и так далее. Интервалы перехода от экспоненциального распределения к синусоидальному и обратно составляют здесь и соответственно, тогда как интервал существования синусоидального распределения между этими переходами составляет .

Таким образом, средняя протяженность интервалов существования основных распределений, синусоидального и экспоненциального, составляет около , тогда как протяженность интервалов переходных распределений (полусинусоидального и линейного) не превышает , то есть составляет около или одну пятую от интервалов основных распределений.

13. Переход между распределениями амплитуды

Рассмотрим несколько более подробно характер изменения распределений амплитуд в слоях на примере частотных зависимостей при достаточно большом соотношении проницаемостей барьеров и промежутков (критерий «достаточности» обсуждается в следующем разделе). Обратимся к рис.5, где показаны зависимости нормированных амплитуд обратно направленной волны в слое №1 (а) и прямо направленных волн в слоях №15 (б) и №16 (в) от частоты падающей волны при соотношении между проницаемостями равным шести.

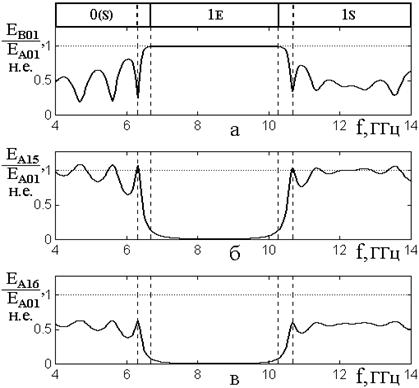
Рис.5. Зависимости нормированных амплитуд обратно направленной волны в слое №1 (а) и прямо направленных волн в слоях №15 (б) и №16 (в) от частоты падающей волны. В верхнем ряду – наименования областей с характерными распределениями амплитуд по слоям: 0(S) – синусоидальное (нулевая зона);

1Е – экспоненциальное (первая зона); 1S – синусоидальное (первая зона).

Параметры материала сред: ; ; ; .

Обозначения областей – те же, что в работе [30].

Из рисунка видно, что в области экспоненциального распределения (1Е) нормированная амплитуда обратно направленной волны в слое №1 близка к единице, то есть структура отражает падающую на нее волну практически полностью. При этом в слоях №15 и №16 амплитуды прямо направленных волн близки к нулю, то есть падающая волна через структуру не проходит.

В областях синусоидального распределения (0(S)) и (1S) амплитуда обратно направленных волн по частоте осциллирует от до Амплитуда прямо направленных волн в слое №15 также осциллирует между и , а в слое №16 – между и Значительное, почти в два раза, уменьшение среднего уровня осцилляций в слое №16 по сравнению со слоем №15 обусловлено свойствами четности этих слоев, подобно тому, как это обсуждалось в работе [30]. Некоторое превышение нормированной амплитуды в слое №15 над единицей, подобное наблюдавшемуся для одномерной волны [30], обусловлено переходом волны от слоя с большой проницаемостью (№14, где ) к слою с малой (№15, где ) и вызвано требованием сохранения потока энергии волны, правила работы с которым подробно разобраны в работе [51].

Переходы между областями с характерными распределениями являются плавными. Таким образом, между областями, соответствующими синусоидальному и экспоненциальному распределениям, имеются переходные области, приближенные границы которых (на уровне ) показаны пунктиром.

Граничные частоты переходных областей, для первой области (по нижнему уровню в точке минимума, по верхнему на уровне ), равны соответственно: и , для второй (по тем же уровням): и . Ширина первой области равна , что составляет около от частоты ее центра (, а ширина второй области – , то есть около от частоты ее центра ().

Ширина переходных областей по мере увеличения соотношения диэлектрических проницаемостей барьера и промежутка уменьшается. Так при и переходная область между зонами 0(S) и 1Е составляет около от центральной частоты, при увеличении до значения уменьшается до , а при составляет всего . То есть переходы между синусоидальным и экспоненциальным распределениями с увеличением отношения проницаемостей становятся более резкими. Тем не менее, в переходных областях по мере изменения частоты переход между распределениями амплитуд всегда остается достаточно плавным: от синусоидального распределения к полусинусоидальному, затем к линейному, которое переходит в экспоненциальное. Переход от экспоненциального распределения к синусоидальному происходит в обратном порядке. Динамика перехода полностью аналогична таковой для одномерной волны, как это подробно рассмотрено в работе [30].

14. Слабая и сильная неоднородность

Рассмотрим теперь частотные зависимости амплитуд волн в слоях при сильной и сильной и слабой степенях неоднородности структуры. Будем различать сильную и слабую степень неоднородности по тому признаку, что в случае слабой неоднородности нормированная амплитуда обратно направленной волны в слое №1, то есть отраженной от структуры в целом, не достигает единицы ни при какой частоте падающей волны. При этом всегда часть энергии волны проходит через структуру, обнаруживая себя на ненулевом уровне в слоях №15 или №16. Заметим, что нулевой уровень здесь в обоих случаях является определенной идеализацией, асимптотически достижимой только при бесконечно большом числе элементов структуры. В реальном же случае рассматриваемой здесь структуры из 16 элементов (слоев) будем полагать критический уровень отражения равным

Обратимся к рис.6, где показаны зависимости нормированных амплитуд обратно направленной волны в слое №1 (а,г) и прямо направленных волн в слоях №15 (б,д) и №16 (в,е) от частоты падающей волны при различных соотношениях между проницаемостями слоев.

Рис.6. Зависимости нормированных амплитуд обратно направленной волны в слое №1 (а,г) и прямо направленных волн в слоях №15 (б,д) и №16 (в,е) от частоты падающей волны при различных соотношениях между проницаемостями слоев. Проницаемость барьера: а, б, в – ; г, д, е – .

Остальные параметры: ; ; .

Из рисунка видно, что в обоих случаях частотные зависимости амплитуды представляют собой чередование ярко выраженных «полос пропускания» и «непропускания», подобных имеющим место в периодической структуре бесконечной протяженности, в аналитическом виде получаемых классическими методами Хилла, Уиттекера, Бриллюэна [1,52,53]. Однако здесь, в отличие от классики, правильная периодичность в какой-то степени нарушается, что особенно хорошо видно из рис.6г-6е, где две «полосы пропускания» между и практически сливаются вместе, оставляя лишь сравнительно узкий неглубокий промежуток вблизи . Можно полагать, что такой характер наблюдаемых зависимостей обусловлен довольно небольшим количеством слоев структуры, насчитывающим всего 8 полных периодов изменения свойств.

Наблюдаются также заметные отличия от случая одномерной волны, рассмотренного в работе [30]. Так для одномерной волны при увеличении волнового числа области пропускания сужаются, причем амплитуда проходящих волн в слое №15 увеличивается, а в слое №16 уменьшается. В рассматриваемом здесь случае электромагнитной волны при увеличении частоты ширина тех и других полос меняется не более чем на , причем нерегулярным образом. Амплитуда как проходящих, так и отраженных волн также не имеет тенденции к систематическому увеличению или уменьшению, причем меняется в ту и другую сторону также на . То есть в нулевом приближении можно считать, что здесь как частотный интервал, так и амплитуда тех и других волн в пределах соответствующих полос практически не меняются (с точностью до ).

Рассмотрим теперь приведенные зависимости с количественной стороны.

Так рис.6а,б,в соответствуют слабой неоднородности: при , то есть проницаемость барьера превышает проницаемость промежутка всего в два раза. В этом случае максимальная амплитуда отраженной волны в слое №1 достигает уровня на частоте , а амплитуда проходящей волны на той же частоте в слое №15 падает до уровня и в слое №16 – до уровня То есть неоднородность, согласно приведенному критерию, является слабой.

Рис.6г,д,е соответствуют сильной неоднородности: при , то есть проницаемость барьера превышает проницаемость промежутка в десять раз. В этом случае максимальная амплитуда отраженной волны в слое №1 превышает критический уровень в интервале частот от до , достигая максимума, равного на частоте . При этом амплитуда проходящей волны в слое №15 падает до уровня ниже , на краях интервала минимума составляя на частоте и на частоте , достигая абсолютного минимума на частоте . Амплитуда проходящей волны в слое №16 падает до уровня ниже , на краях интервала минимума составляя на частоте и на частоте , достигая абсолютного минимума на частоте . Таким образом, неоднородность, согласно приведенному критерию, является сильной.

Основное различие между зависимостями, соответствующими слабой и сильной неоднородностям состоит в том, что при слабой неоднородности зависимости имеют плавный округлый вид, тогда как при сильной они резко очерчены по верхнему и нижнему уровням, то есть их вид близок к прямоугольному. Количество тех и других полос при сильной неоднородности резко возрастает. Так в рассматриваемом интервале частот () на рис.6а наблюдаются четыре колоколообразных максимума, тогда как на рис.6г – уже шесть широких прямоугольных и один узкий колоколообразный, то есть всего – семь. То же можно видеть и при сравнении рис.6б,в с рис.6д,е.

Оценка по формуле (5) для слабой неоднородности при дает частоту , что не соответствует никакой из наблюдаемых полос. В то же время, если взять среднее значение проницаемости между слоями: , а также положить, что длина такого «составного» слоя равна сумме длин барьера и промежутка: , то подставляя эти значения в формулу (5), получаем частоту , что весьма близко соответствует частоте первого максимума на рис.6а ().

Аналогичная оценка для сильной неоднородности при дает частоту , что получается заметно выше верхнего края первого максимума на рис.6г (). В то же время, если взять среднее значение проницаемости барьера и промежутка, а также положить слой «составным», то получаем частоту , что также довольно близко подходит к наблюдаемому значению центра этого максимума , а по минимумам для слоев №15 () и №16 () соответствие получается еще более близким.

Таким образом, можно полагать, что для нахождения центральной частоты первой «области непропускания» более чем (5) подходит следующая формула:

, (66)

где полагается .

Приведенные оценки выполнены для первой наиболее низкочастотной «полосы непропускания». Анализ последующих полос показывает, что их центральные частоты находятся в целочисленном кратном отношении к частоте первой полосы. Получаемое по формуле (66) значение первой из частот, однако является несколько заниженным, так что для повышения точности следует ввести поправочный коэффициент. С такой эмпирической поправкой формулы для расчета центральной частоты -й «полосы непропускания», приобретают вид:

при слабой неоднородности:

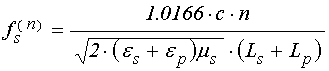, (67)

при сильной неоднородности:

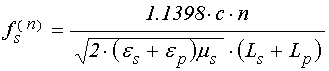. (68)

При промежуточной неоднородности поправочный коэффициент будет иметь промежуточное значение.

15. Изменение соотношения проницаемостей слоев

Рассмотрим теперь трансформацию частотных зависимостей амплитуд при изменении соотношения проницаемостей слоев. С этой целью обратимся к рис.7, где показаны соответствующие зависимости для нормированной амплитуды волны обратного направления в слое №1 (), то есть амплитуды отраженной волны от структуры в целом. Частотные зависимости амплитуд волн прямого направления в слоях №15 и №16 ведут себя сходным образом, поэтому далее не рассматриваются.

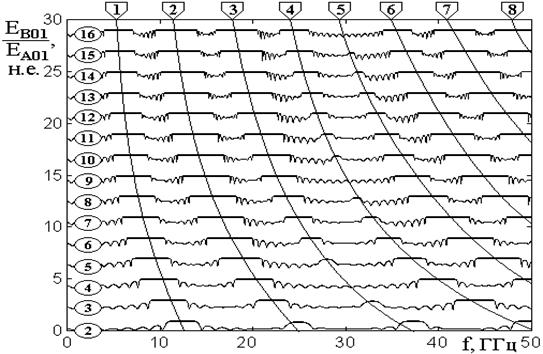
Рис.7. Зависимости нормированной амплитуды обратно направленной волны в слое №1 от частоты
при различных соотношениях проницаемостей слоев.

Числа в кругах около вертикальной оси слева – отношение проницаемостей барьера и промежутка . Остальные параметры слоев – те же.

При построении зависимостей каждая последующая кривая была смещена вверх по отношению к предыдущей на , то есть нулевой уровень каждой кривой, соответствующей заданному в кругу значению , приходится на Горизонтальные участки кривых, выделенные утолщенными линиями, соответствуют , то есть полному отражению падающей волны от структуры в целом. Наклонные кривые проведены через середины горизонтальных участков.

Из рисунка видно, что по мере увеличения соотношения проницаемостей центральные частоты «полос непропускания» снижаются, причем тем сильнее, чем номер полосы выше. То есть происходит как бы сгущение полос в направлении к нулю частоты. Однако при таком сгущении явного взаимного соотношения места, занимаемого отдельными полосами, не наблюдается, хотя некоторые полосы (№3, 4, 5 и в какой-то степени №2) испытывают сужение с последующим расширением. Так например, полоса №4 при имеет ширину около , которая при сужается до нуля, а при снова расширяется, составляя около . При этом расстояние между окружающими ее полосами №3 и №5 во всем интервале изменения монотонно уменьшается с до , не претерпевая никакого локального сужения в окрестности .

Таким образом, сгущение полос при увеличении происходит довольно равномерно по всем полосам во всем исследованном диапазоне частот.

Заключение

Рассмотрено распространение волн прямого и обратного направлений в многослойной структуре ограниченной длины с периодической неоднородностью меандрового типа, представляющей собой чередование двух видов слоев равной толщины с различающимися параметрами.

В качестве расчетного аппарата использован метод пошагового алгоритма, первоначально разработанный для одномерных волн. В данной задаче метод обобщен на случай трехмерных электромагнитных волн, показана возможность его реализации с использованием комплексных адмиттансов и волновых чисел сред, составляющих структуру. Приведена схема и аналитическая реализация метода пошагового алгоритма для случая сред с произвольными диэлектрической и магнитной проницаемостями, а также проводимостями.

Исследованы частотные зависимости амплитуд волн прямого и обратного направлений в крайних слоях структуры. Показано, что такие зависимости имеют квазирезонансный характер в виде большого центрального лепестка, с обеих сторон сопровождаемого меньшими лепестками-сателлитами. Предложена модель структуры как цепочки последовательно соединенных полуволновых резонаторов. Показано, что частота главного лепестка определяется в первую очередь диэлектрической проницаемостью барьера, но отклоняется от резонансной частоты полуволнового барьера вниз тем сильнее, чем больше различие диэлектрических проницаемостей барьера и промежутка.

Исследована трансформация частотных характеристик при изменении числа барьеров. Показано, что по мере увеличения числа барьеров количество лепестков увеличивается, причем между основными, определяемыми резонансными свойствами барьера, появляются промежуточные, связанные с интерференцией волн при распространении между барьерами. Получены аналитические формулы, позволяющие рассчитать частоты основных лепестков, положения их максимумов и минимумов между ними при заданном числе барьеров.

Исследовано распределение амплитуд волн во внутренних слоях структуры при большом различии параметров между барьерами и промежутками. Показано, что по зависимости амплитуд от координаты вдоль оси структуры преобладают два главных вида распределения – синусоидальное и экспоненциальное, по частоте поочередно переходящие друг в друга через посредство промежуточных распределений – полусинусоидального и линейного. Выявлено, что частотные интервалы существования главных распределений превышают таковые для промежуточных не менее чем в несколько раз, причем при увеличении различия параметров барьеров и промежутков такое превышение увеличивается. Показано, что как при вариации параметров, так и при изменении частоты переход основных распределений друг в друга через промежуточные всегда происходит плавно, однако частотные интервалы переходных распределений с увеличением различия параметров слоев сужаются.

Исследованы особенности частотных зависимостей амплитуды отраженной и проходящей волн в широком диапазоне частот при различных степенях неоднородности структуры. Введены определения сильной и слабой неоднородностей и получен критерий перехода между ними, определяемый величиной различия диэлектрических проницаемостей барьера и промежутка. Показано, что как при слабой, так и особенно при сильной неоднородностях частотные зависимости амплитуды представляют собой чередование ярко выраженных «полос пропускания» и «непропускания», подобных имеющим место в периодической структуре бесконечной протяженности, в аналитическом виде получаемых классическими методами.

Выявлено не отмеченное классикой нарушение правильной периодичности наблюдаемых зависимостей, состоящее в изменении частотной ширины полос вплоть до полного их исчезновения или слияния с соседними. В качестве возможной причины такого нарушения предложен ограниченный характер полного числа слоев структуры по сравнению с классическим случаем, где такое ограничение отсутствует. Для расчета центральных частот полос непропускания предложена эмпирическая формула, включающая в себя усредненное значение проницаемостей слоев в сочетании с близким к единице поправочным коэффициентом, увеличивающимся по мере увеличения степени неоднородности.

Рассмотрена трансформация частотных зависимостей в широком интервале изменения соотношения проницаемостей слоев. Показано что при увеличении этого соотношения частоты середин полос того и другого вида снижаются, а их ширина также уменьшается, то есть полный спектр полос как бы поджимается к своему низкочастотному концу, причем это стремление выражено тем сильнее, чем частота полосы выше.

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

Литература

1. Бриллюэн Л., Пароди М. Распространение волн в периодических структурах. М.: ИЛ. 1959.

2. Бреховских Л.М. Волны в слоистых средах. М.: Наука. 1973.

3. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука. 1989.

4. Elachi C. // Proc. of the IEEE. 1976. V.64. №12. P.1666.

5. Анненков А.Ю., Виноградов А.П., Герус С.В., Рыжиков И.А., Шишков С.А., Иноуе М. // Известия РАН. Серия физическая. 2007. Т.71. №11. С.1612.

6. Бутько Л.Н., Бучельников В.Д., Бычков И.В., Шавров В.Г. // Журнал радиоэлектроники [электронный журнал]. 2007. №3. URL:

http://jre.cplire.ru/jre/mar07/3/text.html

7. Pendry J.B. // Phys. Rev. Lett. 2000. V.85. P.3966.

8. Smith D.R., Padilla W.J., Vier D.C., Nemat-Nasser S.C., Schultz S. // Phys. Rev. Lett. 2000. V.84. №18. P.4184.

9. Виноградов А.П. Электродинамика композитных материалов. М.: УРСС. 2001.

10. Lindell I.V., Tretyakov S.A., Nikoskinen K.I., Ilvonen S. // Micr. Opt. Tech. Lett. 2001. V.31. №2. P.129.

11. Parimi P.V., Lu W.T., Vodo P., Sokoloff J., Derov J.S., Sridhar S. // Phys.Rev.Lett. 2004. V.92. №12. P.127401(4).

12. Агранович В.М., Гартштейн Ю.Н. // УФН. 2006. Т.176. №10. С.1052.

13. Веселаго В.Г. // УФН. 2011. Т.181. №11. С.1201.

14. Вендик И.Б., Вендик О.Г. // ЖТФ. 2013. Т.83. №1. С.3.

15. Гуляев Ю.В., Никитов С.А., Животовский Л.В., Климов А.А., Тайад Ф., Пресманес Л., Бонин К., Цай Ч.С., Высоцкий С.Л., Филимонов Ю.А. // Письма в ЖЭТФ. 2003. Т.77. №10. С.670.

16. Гуляев Ю.В., Никитов С.А., Волков А.И. // РЭ. 2007. Т.50. №9. С.1107.

17. Кирюхин Н.Н., Лисовский Ф.В. // ФТТ. 1968. Т.10. №3. С.709.

18. Зубков В.И., Моносов Я.А., Щеглов В.И. // Письма в ЖЭТФ. 1971. Т.13. №5. С.229.

19. Медников А.М., Никитов С.А., Попков А.Ф. // ФТТ. 1982. Т.24. №10. С.3008.

20. Зубков В.И., Щеглов В.И. // РЭ. 2011. Т.56. №7. С.839.

21. Вороненко А.В., Герус С.В. // Письма в ЖТФ. 1984. Т.10. №12. С.746.

22. Вороненко А.В., Герус С.В., Харитонов В.Д. // Изв. ВУЗов. Физика. 1988. Т.31. №11. С.76.

23. Анненков А.Ю., Герус С.В., Сотников И.В. // РЭ. 1992. Т.37. №8. С.1371.

24. Анненков А.Ю., Герус С.В. // РЭ. 1996. Т.41. №2. С.216.

25. Герус С.В. Магнитостатические волны в пространственно-периодических и двумерно-неоднородных магнитных полях. Диссертация на соискание ученой степени д.ф.-м.н. Москва. 2012.

26. Вороненко А.В., Герус С.В., Красножен Л.А. // Микроэлектроника. 1989. Т.18. №1. С.61.

27. Григорьева Н.Ю. Дипольно-обменные спиновые волны в периодических структурах на основе тонких ферромагнитных пленок. Диссертация на соискание ученой степени к.ф.-м.н. Санкт-Петербург. 2009.

28. Григорьева Н.Ю., Калиникос Б.А. // ЖТФ. 2009. Т.79. №8. С.110.

29. Дроздовский А.В. Исследование сверхвысокочастотных свойств магнонных кристаллов на основе ферромагнитных пленок. Диссертация на соискание ученой степени к.ф.-м.н. Санкт-Петербург. 2011.

30. Антонец И.В., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2015. №1. URL: http://jre.cplire.ru/jre/jan15/1/text.html

31. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №1. С.67.

32. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №1. С.16.

33. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №1. URL:

http://jre.cplire.ru/jre/jan13/11/text.pdf

34. Антонец И.В., Щеглов В.И. Алгоритмы определения амплитуд отраженных и проходящих волн при распространении встречных волн в многослойных неоднородных структурах. Часть первая. Укороченный алгоритм. Учебное пособие (электронное). Сыктывкар: ИПО ФГБОУ ВПО СыктГУ. 2013.

35. Антонец И.В., Щеглов В.И. Алгоритмы определения амплитуд отраженных и проходящих волн при распространении встречных волн в многослойных неоднородных структурах. Часть вторая. Полный алгоритм. Учебное пособие (электронное). Сыктывкар: ИПО ФГБОУ ВПО СыктГУ. 2013.

36. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть пятая. Алгоритмические методы. Сыктывкар: ИПО СыктГУ. 2014.

37. Антонец И.В., Щеглов В.И. Распространение волн через тонкие слои и пленки. Сыктывкар: ИПО СыктГУ. 2010.

38. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №2. С.133.

39. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть первая. Прямой метод. Сыктывкар: ИПО СыктГУ. 2011.

40. Калашников С.Г. Электричество. М.: Наука. 1964.

41. Сивухин Д.В. Общий курс физики. Т.3. Электричество. М.: Наука. 1977.

42. Никольский В.В, Никольская Т.И. Электродинамика и распространение радиоволн. М.: Наука. 1989.

43. Левич В.Г. Курс теоретической физики. Т.1. М.: Наука. 1969.

44. Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. М.: Высшая школа. 1974.

45. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.

46. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.

47. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2007. Т.52. №4. С.403.

48. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2008. Т.53. №4. С.389.

49. Ландсберг Г.С. Оптика. М.: Наука. 1976.

50. Борн М., Вольф Э. Основы оптики. М.: Наука. 1970.

51. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №10. С.1171.

52. Уиттекер Э.Т., Ватсон Д.Н. Курс современного анализа. Ч.2.М.: ИЛ. 1963.

53. Мак-Лахлан Н.В. Теория и приложения функций Матье. М.: ИЛ. 1953.