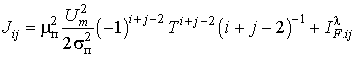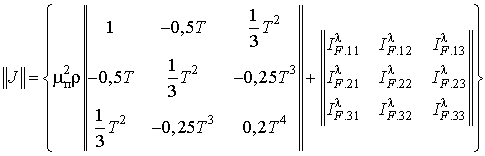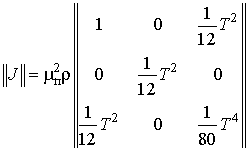УДК 681.3

Оценка погрешности измерения ВЕКТОРНОГО информационного параметра СИГНАЛА на фоне

аддитивнЫХ НЕКОРРЕЛИРОВАННЫХ негауссовскИХ помех

 

В. М. Артюшенко¹, В. И. Воловач²

¹ГБОУ ВО МО «Технологический университет», г. Королев

²ФГБОУ ВПО «Поволжский государственный университет сервиса», г. Тольятти

 

Статья поступила в редакцию 4 декабря 2015 г.

 

Аннотация. Рассмотрены вопросы, связанные оценкой точности измерения векторного информационного параметра сигнала, несущих сведения о движении протяженных объектов, на фоне аддитивной некоррелированной негауссовской помехи. Показано, что учет негауссовского характера воздействующей аддитивной помехи позволяет значительно повысить точность оцениваемого параметра, причем, чем больше плотность распределения вероятности аддитивной помехи отличается от гауссовской, тем выше получаемый выигрыш. Получены выражения для оценки точности измерения информационных параметров сигнала на фоне некоррелированных в общем случае негауссовских аддитивных помех. Показано, что учет негауссовского характера аддитивной помехи позволяет значительно повысить точность измерения информационных параметров.

Ключевые слова: радиолокационный измеритель, протяженный объект, аддитивная некоррелированная негауссовская помеха, информационные параметры сигнала.

Abstract. We considered the issues related to the estimation of measurement accuracy of vector information parameters of the signal, carrying the information about the motion of extended objects along with the additive uncorrelated non-Gaussian noise. It is demonstrated that taking into account the non-Gaussian nature of the actuating additive noise can significantly improve the accuracy of the estimated parameter and the greater is the difference between the probability density of the additive noise and Gaussian noise, the higher is the gain achieved. We obtained the expressions for estimating the accuracy of measurement of information parameters of the signal along with the correlated, in general, non-Gaussian additive noise. It is demonstrated that taking into account non-Gaussian nature of the additive noise can significantly improve the measurement accuracy of the information parameters.

Key words: radar meter, extended object, additive correlated non-Gaussian noise, information parameters of the signal.

Введение

Вопросы измерения (оценки) параметров сигналов, несущих информацию о движении объектов, в радиолокации являются традиционными и весьма подробно рассмотрены в [1, 2, и др.], включая вопросы радиолокационного измерения точечных [3, 4] и отчасти сложных дискретных [5, 6] целей. Вместе с тем многие аспекты, связанные с измерением информационных, в частности, векторных, параметров сигнала, несущих сведения о движении объектов, находящихся на относительно небольших расстояниях от радиолокационных измерителей (РИ), являются ещё недостаточно изученными и имеют ряд специфических особенностей как теоретического, так и практического характера [7]. Отметим, что при оценке погрешности (точности) информационных параметров сигнала наибольший интерес представляет собой случай одновременного изменения частоты, ее производной и фазы полезного сигнала. Вместе с тем, немаловажной, в том числе и для рассматриваемых в настоящей статье вопросов, является и оценка погрешности измерения скалярного информационного параметра сигнала, рассмотренная авторами ранее [8]. 

В большинстве работ, посвященных вопросам оценки параметров сигналов, считалось, что на полезный сигнал воздействует аддитивная помеха, описывающаяся, как правило, гауссовской плотностью распределения вероятности (ПРВ). Однако, как показывают проведённые исследования [9-11], принимаемый измерителем сигнал подвержен воздействию аддитивных, в том числе и некоррелированных помех, имеющих ярко выраженный негауссовский характер с независимыми значениями для частоты, производной частоты и фазы полезного сигнала. Для радиолокации, радионавигации, телеметрии, радиоизмерительной техники представляет значительный интерес получить оптимальную оценку параметров обрабатываемых сигналов при наличии помех с произвольной ПРВ, включая возможность учета влияния степени отличия ПРВ аддитивной помехи от гауссовской на точность оцениваемого параметра.

Для обеспечения наивысшей точности измерения информационных параметров необходимо оценить их оптимальным образом. Методы решения задачи оптимальной оценки параметров сигнала можно получить, основываясь на математическую статистику и теорию нелинейной фильтрации [1, 12].

Задачу оценивания информационных параметров сигнала будем проводить по методу максимума апостериорной ПРВ (АПРВ). Для определения количественных оценок измеряемых параметров используем нижние границы неравенства Крамера-Рао [12]. Считаем, что сигнал содержит совокупность параметров , подлежащих измерению (оцениванию), причем на интервале наблюдения эти параметры остаются неизменными.

Отметим, что в нашем случае оценке будут подлежать только неэнергетические информационные параметры полезного сигнала. Считается, что оценки являются функциями достаточных статистик и обладают асимптотическими свойствами состоятельности, как правило, несмещенности и нормальности.

Оценка погрешности измерения векторного информационного параметра на фоне аддитивной некоррелированной негауссовской помехи

Рассмотрим случай одновременного измерения (оценки) нескольких информационных параметров полезного сигнала , , на фоне воздействия негауссовской аддитивной помехи, имеющей некоррелированный характер.

Оценку точности рассмотрим на примере одновременного измерения ω,  и φ полезного сигнала

,                                   (1)

несущих информацию о параметрах движения лоцируемого объекта.

Будем считать, что оценка измеряемых параметров осуществляется на интервале наблюдения [0, T], причем моменты времени, соответствующие началу и концу обрабатываемого сигнала точно известны и совпадают с границами интервала наблюдения.

Воспользуемся методикой, изложенной [13] для определения одновременной оценки информационных параметров сигнала на фоне гауссовской некоррелированной помехи.

Для удобства проведения дальнейшего анализа представим полезный сигнал  в виде

,                                  (2)

где ; ; .

Заметим, что в нашем случае при оценке информационных параметров по максимуму АПРВ должны выполняться три уравнения:

;     ;     .

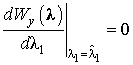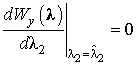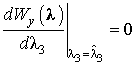Выражение нижней границы неравенства Крамера-Рао для дисперсии несмещенных совместных параметров полезного сигнала  запишется [9]

; i, j = 1, 2, 3,                                         (3)

где  – алгебраическое дополнение элемента J_ij информационной матрицы Фишера , в которой индексы ij определяют изменяемый информационный параметр сигнала: частоту w, производную частоты и фазу  ;  – определитель матрицы  [14].

Заметим, что элементы информационной матрицы при  учитывают взаимную зависимость оцениваемых параметров. В случае если измеряемые параметры не зависят друг от друга, информационная матрица упрощается:

.

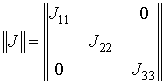Дисперсия того или иного параметра будет определяться выражением:

; i, j = 1, 2, 3.

Элементы матрицы определяются соотношением

.             (4)

Здесь:  – целая часть отношения;  – интервал взятия временных отсчетов; t₁ – начало времени измерения;  – производная от обрабатываемого полезного сигнала по оцениваемому параметру , определяемая при ;  – составляющая информационной матрицы Фишера относительно измеряемых параметров, заключенная в совместной ПРВ оцениваемых параметров ;  – производная по параметру , определяемая при  от весовой функции , являющаяся решением:

,

где  – корреляционная функция помехи.

В случае d-коррелированного шума

,

где  – спектральная плотность помехи. Выражение (4) примет вид:

,                                 (5)

где – дисперсия воздействующей помехи в полосе .

Для обрабатываемого сигнала производные будут определяться:

, i = 1, 2, 3.                 (6)

Сделав необходимые тригонометрические преобразования, получим

,   (7)

где принято, что  t = 0, то есть интервал измерения соответствует –Т ≤ t ≤ 0.

Считая, что оцениваемые информационные параметры на интервале измерения остаются неизменными, принимаем, что их величины равны значениям, принимаемым в момент времени окончания интервала измерения.

При значении косинуса в (7), равном единице, что равносильно допущению ωT >> 1, и большом числе отсчетов () на интервале оценки информационных параметров получим:

,                 (8)

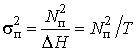где  ;  – дисперсия аддитивной помехи.

Обозначив через , играющее в данном случае роль обобщенного отношения сигнал/помеха (ОСП), запишем матрицу  в виде:

.   (9)

Если ПРВ измеряемых (оцениваемых) параметров

,

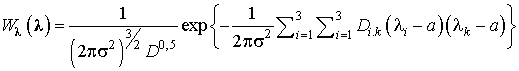где s² и а – соответственно, дисперсия и среднее значение; D – детерминант матрицы  элементы которой  представляют значения нормированной корреляционной функции;  – алгебраическое дополнение элемента  в матрице, то информационная матрица

 в (9), примет вид:

.

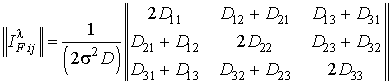При оценке информационных параметров методом максимального правдоподобия корреляционная матрица ошибок (9) примет вид:

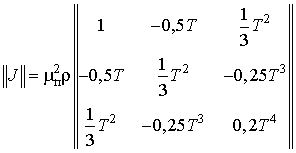.                             (9а)

Определитель матрицы в этом случае будет равен:

.

Подставляя (8) и (9) в (3), зная, что , после несложных преобразований получим выражение для определения оценок нижних границ неравенства Крамера-Рао информационных параметров полезного сигнала (1) при воздействии негауссовских аддитивных помех с независимыми значениями, которые будут иметь следующий вид:

– для частоты 

;                                         (10а)

– для производной частоты 

;                                         (10б)

– для фазы 

.                                            (10в)

Если объект движется с постоянной скоростью, то есть , то

;                                          (11)

.                                            (12)

Если начальная фаза колебания известна, а частота постоянна, то

.                                         (13)

В тех случаях, когда объект является неподвижным, то есть необходимо измерить только фазу обрабатываемого сигнала (при известной частоте)

.                                            (14)

Если значения информационных параметров полезного сигнала принимаются равными их значениям в момент, совпадающий с серединой интервала измерения, выражение для определения элементов матрицы  имеет вид:

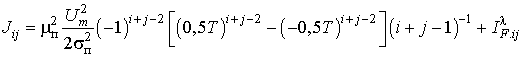.  (15)

При оценке информационных параметров методом максимального правдоподобия матрица  запишется:

.                                      (16)

Откуда .

В этом случае:

–  для частоты

;                                         (17а)

–  для производной частоты

;                                        (17б)

– для фазы 

.                                           (17в)

Сравнение (11) и (17) показывает, что нижние границы дисперсии оценок  и  значительно меньше, если привязка измерений осуществляется к середине интервала наблюдения. Повышение точности измерения при такой привязке связано с тем, что в этом случае, как видно из (16), недиагональные элементы J₁₂, J₂₁, J₂₃ и J₃₂ равны нулю и лишь элементы J₁₃ и J₃₁ отличны от него.

В случае отличия от нуля недиагональных элементов в матрице  следует учитывать наличие корреляционных связей между ошибками оценок отдельных измеряемых параметров.

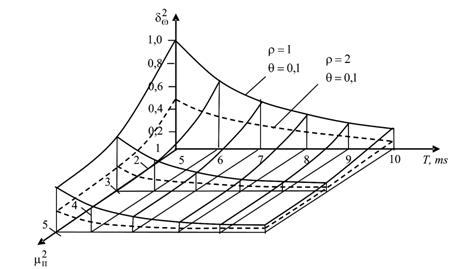
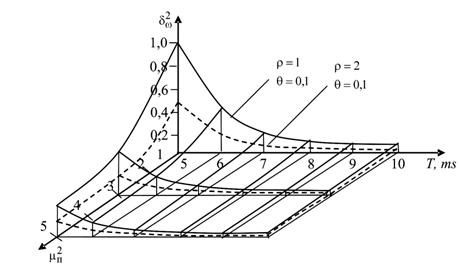
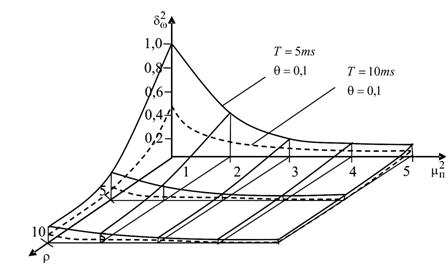
На рис. 1 (; б – ; в – зависимость ) представлены зависимости, иллюстрирующие приведенные погрешности  измерения (оценки) информационных параметров  сигнала , несущих информацию о параметрах движения лоцируемого объекта, для случая, когда величины j, w и  принимаются равными значениям в момент окончания интервала измерения.

Из графиков видно, что с увеличением r, Т и  приведенная погрешность измерения (оценки) уменьшается, а значит, точность измерения возрастает.

Как видно, учет негауссовского характера воздействующей аддитивной некоррелированной помехи позволяет значительно повысить точность оцениваемого параметра, причем, чем больше ПРВ аддитивной помехи отличается от гауссовской, тем выше получаемый выигрыш.

Выводы

Таким образом, получены выражения для оценки точности измерения информационных параметров сигнала, несущих сведения о движении протяженных объектов, на фоне аддитивных некоррелированных негауссовских помех.

Показано, что учет негауссовского характера воздействующей аддитивной помехи позволяет значительно повысить точность оцениваемого параметра, причем, чем больше плотность распределения вероятности аддитивной помехи отличается от гауссовской, тем выше получаемый выигрыш.

 

а)

б)

в)

Рис. 1. Зависимости

 

Работа выполнена в рамках фундаментальной НИР, финансируемой из средств Минобрнауки РФ (Государственное задание на 2014, 2015 гг., № ГР 01201458513).

 

Литература

 

1. Сосулин Ю. Г. Теоретические основы радиолокации и радионавигации: учеб. пособие для вузов. М.: Радио и связь, 1992. 304 с.

2. Финкельштейн М. И. Основы радиолокации. М.: Радио и связь, 1983. 536 c.

3. Журавлев А. К., Лукошкин А. П., Поддубный С. С. Обработка сигналов в адаптивных антенных решетках. Л.: ЛГУ, 1983. 240 c.

4. Родимов А. П., Поповских В. В. Статистическая теория поляризационно-временной обработки сигналов и помех. М.: Радио и связь, 1984. 272 с.

5. Радиолокационные характеристики летательных аппаратов / М. Е. Марганов, Ю. С. Зиновьев, Л. Ю. Астанин и др.; под ред. Л. Т. Тучкова. М.: Радио и связь, 1985. 236 с.

6. Фалькович С. Е., Хомяков Э. Н. Статистическая теория измерительных радиосистем. М.: Сов. радио, 1981. 288 c.

7. Артюшенко В. М. Обработка информационных параметров сигнала в условиях аддитивно-мультипликативных негауссовских помех. Королев МО: ФГБОУ ВПО ФТА, Изд-во «Канцлер», 2014. 298 c.

8. Артюшенко В. М., Воловач В. И. Оценка погрешности измерения скалярного информационного параметра движущегося протяженного объекта на фоне аддитивных негауссовских помех // Журнал радиоэлектроники. 2015. № 1. С. 4. [Электронный ресурс]. URL: http://jre.cplire.ru/jre/jan15/12/text.html

9. Оптимальный прием пространственно-временных сигналов в радиоканалах с рассеянием / Под ред. С. Е. Фальковича. М.: Радио и связь, 1989. 295 c.

10. Валеев В. Т., Сосулин Ю. Г. Обнаружение слабых когерентных  сигналов в коррелированных негауссовских помехах // Радиотехника и электроника. 1969. Т.14. № 2. С. 230–238.

11. Артюшенко В. М., Воловач В. И. Оценка погрешности измерения параметров движения протяженных объектов в условиях изменяющейся дальности // Известия вузов. Радиоэлектроника. 2015. Т. 58. № 1. С. 26–37.

12. Тихонов В. И. Оптимальный прием сигналов. М.: Радио и связь, 1983. 320 c.

13. Тихонов В. И., Кульман Н. К. Нелинейная фильтрация и квазикогерентный приём сигналов. М.: Сов. радио, 1975. 704 c.

14. Вопросы статистической теории радиолокации / П. А. Бакут, И. А. Большаков, Б. М. Герасимов и др.; под ред. Г. П. Тартаковского. Т.2. М.: Сов. радио, 1964. 1086 c.