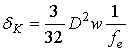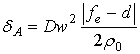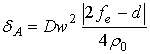УДК 629.396.67

Исследование и минимизация аберраций в двухзеркальнОЙ осесимметричнОЙ системЕ ШВАРЦШИЛЬДА

 

В. А. Калошин, Е. В. Фролова

Институт радиотехники и электроники им. В.А. Котельникова РАН

 

Статья получена 12 марта 2015 г.

 

Аннотация. Представлены результаты исследования аберраций в осесимметричных двухзеркальных системах Шварцшильда с использованием метода трассировки лучей. Предложен алгоритм анализа и минимизации аберраций наклонных меридиональных и сагиттальных лучей в области фокусировки, который учитывает аберрации высших порядков. Получены зависимости радиуса пятна рассеяния от параметров зеркал, позволяющие определять параметры, обеспечивающие максимальные углы зрения. Приведены примеры оптимизации зеркальной системы и характеристики сканирования, рассчитанные методом физической оптики. Сопоставлены результаты оптимизации, полученные с использованием методов трассировки лучей и физической оптики.

 Ключевые слова: осесимметричные двухзеркальные системы, многолучевые антенны, апланатическая система Шварцшильда, минимизация аберраций.

Abstract. Results of research of aberrations in Sсhwarzschild symmetric two-mirror systems with use of ray tracing technique are presented. The algorithm of analysis and minimization of aberrations of inclined meridional and sagittal rays in the focus area with considering highest orders aberrations is proposed. The dependences of scattering spot radius on parameters of mirror system to determine parameters with providing the maximum angles of view are received. The examples of mirror system optimization and scanning characteristics  calculated using method of physical optics are given. The results of optimization obtained with use of physical optics and ray tracing technique are compared.

Key words: symmetric two-mirror systems, multibeam antennas, Sсhwarzschild aplanatic system, minimization of aberrations.

 

Введение

Точное аналитическое решение, описывающее форму зеркал апланатической двухзеркальной системы, удовлетворяющее условию синусов Аббе и обеспечиваюшее отсутствие аберраций, зависящих от первой степени угла зрения, было получено К. Шварцшильдом в [1]. Условие, при котором в апланате Шварцшильда устраняется астигматизм, было использовано Кудэ [2] при попытке создания телескопа апланата-анастигмата, и соответствующая зеркальная система получила название Шварцшильда-Кудэ. Несмотря на очевидные достоинства, точное решение Шварцшильда не было востребовано при построении оптических систем, что было обусловлено сложностью изготовления асферических поверхностей зеркал с требуемой точностью. Развитие оптической теории аберраций в зеркальных телескопах [1-4] способствовало широкому распространению оптических систем с образующими зеркал, представляющими собой конические сечения, которые являются апланатическими лишь в приближении теории аберраций третьего порядка. Самая распространённая среди таких систем – система Ричи-Кретьена [3], в которой оба зеркала имеют форму гиперболоида. Длительное время аберраций третьего порядка было достаточно для описания некогерентных оптических систем, так как рассматривались небольшие поля зрения – не превышающие долей градуса.

В работе [5] приведены результаты детальных исследований и сравнение аберраций в апланатических телескопах, выполненных по различным схемам. Представленный анализ выполнен традиционно в рамках приближения аберраций третьего порядка для поверхностей в виде конических сечений. В частности, один из вариантов анастигмата по схеме Шварцшильда рассматривается не как точного решение, а в виде приближения, при котором обе поверхности зеркал, главного и вспомогательного, – сферические. Работа [6] представляет часть систематического исследования различных конфигураций апланатических систем и посвящена анализу аберраций в двухзеркальном телескопе Шварцшильда-Кудэ. Исследование выполнено, как и в [5], для конических поверхностей, скорректированных в 3-м порядке теории аберраций. Анализ аберраций не выявил однозначного преимущества какой-либо из рассмотренных зеркальных систем. В тоже время в работе [7] в результате сравнения системы Шварцшильда-Кудэ и камеры Шмидта, было показано, что система Шварцшильда-Кудэ может превосходить систему Шмидта по качеству изображения.

Следует еще раз заметить, что во всех приведенных работах не использовалось точное решение Шварцшильда. Сопоставление различных вариантов апланата Шварцшильда показали его преимущество по сравнению с телескопами Ричи-Кретьена и Грегори-Максутова при малых эквивалентных фокусных расстояниях [8]. Отметим, что для проведения данного исследования автором работы [8] было выполнено соответствующее расширение класса поверхностей в оптической программе ZEMAX, использующей метод трассировки лучей.

Развитие технологий изготовления больших асферических зеркал позволило реализовать точное решение Шварцшильда при построении современных γ-телескопов [9,10] с использованием схемы Шварцшильда-Кудэ.

         Практически независимо от исследований, проводимых при разработке  оптических телескопов, проводились исследования аберраций  в зеркальных антенных системах и их влияния на характеристики сканирования. В одной из первых публикаций в этой области [11] исследовались аберрации фазы в апертуре главного зеркала в параболическом зеркале, в классической системе Кассегрена и в апланатической системе Шварцшильда, полученные при использовании метода трассировки лучей.  Было показано, что преимущество апланатической системы проявляется лишь при углах зрения не более пяти градусов.  Основной вывод,  к которому пришли авторы работы, заключался в том, что в классе широкоугольных систем при реализации углов зрения более 15 градусов  апланатическая система не может конкурировать с тороидальными и сферическими зеркалами, что главным образом связано с большими размерами вспомогательного зеркала, требуемыми для перехвата наклонных лучей.  Названы перспективы использования апланатов Шварцшильда – либо при использовании вспомогательного зеркала с поворотом поляризации, либо в планарных многослойных системах.

В работах [12-14] получены характеристики сканирования антенн на основе двухзеркальной системы Шварцшильда в виде зависимостей усиления, а в работе [15] -  коэффициента использования поверхности (КИП) методом физической оптики. Показано, что для случая системы с малым вспомогательным зеркалом и малыми продольными размерами, сектор сканирования не превышает нескольких градусов. Как следует из выводов, сделанных в работе [12], нет никаких оснований для предпочтения апланатической системы Шварцшильда перед классической системой Кассегрена. Следует заметить, что в этих исследованиях, как будет показано далее, рассматривалась та область параметров, где аберрации в системе Шварцшильда велики.

В [16,17] приведены результаты обширных исследований двухзеркальных антенн, в том числе апланатических. В этих работах методом трассировки лучей детально изучены аберрации в некоторых реализациях апланата Шварцшильда, приведены параметры лучших апланатов и указана возможность реализации поля зрения более 90 градусов.

В работе [18] исследованы аберрации в апланатических и классических двумерных планарных зеркальных системах. Исследования, в частности,  показали, что для описания широкоугольных апланатических зеркальных систем с малыми продольными размерами недостаточно теории аберрации третьего порядка. В этой области параметров для меридиональных лучей характерно наличие комы и боковой сферической аберрации высших порядков. Предложенный алгоритм минимизации поперечных несимметричных аберраций меридиональных лучей позволил определить параметры оптимальной планарной апланатической зеркальной системы, основанной на точном решении Шварцшильда. Было показано, что при больших электрических размерах главного зеркала сектор сканирования апланата почти в два раза больше, чем сектор сканирования планарного параболического зеркала, и при минимизации аберраций в виде комы высших порядков и сравнительно небольших электрических размерах апертуры его величина может превышать 90°. Оптимизированная планарная трехслойная многолучевая двухзеркальная система Шварцшильда была реализована и экспериментально исследована в работе [19].

В работах [20,21] изложен новый подход к исследованию аберраций в зеркальных системах и представлена теория аберраций, основанная на разложение эйконала в апертуре главного зеркала по степеням поперечного и продольного смещений источника из фокуса. Один из результатов теории – условие отсутствия астигматизма - при приближении к оси исследуемой точки апертуры переходит в условие, известное из оптической теории. При учете трех членов разложения аналитические соотношения, полученные в рамках этой теории для планарных систем [21], позволяют исследовать и оптимизировать аберрации без использования трассировки лучей даже в случае больших углов зрения.

Таким образом, несмотря на большое количество работ, посвященным апланатическим зеркальным системам, результаты опубликованных исследований осесимметричной системы Шварцшильда характеризуют лишь частные случаи набора параметров. Эти результаты порой противоречивы и не дают полной картины аберраций во всей области изменения параметров и широком диапазоне углов зрения. В большинстве оптических работ не используется точное решение Шварцшильда для апланатических двухзеркальных систем и не учитываются аберрации высших порядков, которые становятся заметны при увеличении углов зрения и уменьшении продольных размеров систем. С другой стороны в исследованиях двухзеркальных антенн, мало используются результаты оптической теории аберраций, позволяющие в первом приближении определять области с минимальными аберрациями и затем проводить более детальный анализ с учетов влияния аберраций высших порядков.

Цель данной работы – развитие методики анализа и минимизации аберраций, в том числе высших порядков, в осесимметричных двухзеркальных апланатических системах с использованием метода трассировки лучей и ее применения для исследования апланата Шварцшильда в широком диапазоне углов зрения и геометрических параметров. Следует отметить, что подобный анализ аберраций меридиональных лучей в апланате Шварцшильда был проведен в работе [18], где методом трассировки лучей по критерию среднеквадратичной аберрации (СКА) проанализированы планарные системы, и эти результаты будут использованы в данной работе. Кроме того, в данной работе также будет проведен анализ сагиттальных лучей.

 

Метод трассировки лучей

Метод трассировки лучей широко используется в геометрической оптике (ГО) в двух вариантах. Эти варианты отличаются направлением хода лучей в зеркальной системе. В оптической теории аберраций принято использовать метод трассировки, в котором рассматриваются лучи, падающие на главное зеркало под углом к его оси. Эти лучи, пройдя оптическую систему, фокусируются в области, называемой областью рассеяния, создавая тот или иной вид каустики. Анализ формы и размера пятна рассеяния позволяет исследовать возникающие аберрации. В соответствии с классической теорией  [22] аберрации эйконала в области фокусировки представляются в виде двойных рядов по степеням апертурного угла F/D (D- диаметр главного зеркала, F - фокусное расстояние) и угла зрения w. Каждый член разложения характеризует тот или иной вид аберраций. Коэффициенты при членах разложения, зависящие от закона отображения и параметров системы, могут быть минимизированы выбором параметров. В приближении теории аберраций третьего порядка в апланатических системах отсутствуют аберрации в виде комы. Вид разложения по степеням угловых переменных накладывает очевидные ограничения на применение теории. Эта теория с успехом применяется для длиннофокусных телескопов с небольшими углами зрения. В зеркальных антенных системах микроволнового диапазона волн требуются углы зрения, составляющие десятки градусов при ограничении на продольные размеры системы. В случае широкоугольных короткофокусных систем в разложении становятся существенными аберрации высших порядков [22,23], для коэффициентов которых нет аналитических формул, и минимизация аберраций в этом случае проводится численно [18]. Один из результатов трассировки в данном случае – это возможность определения оптимального положения элементов облучающей системы и использования этих данных в качестве начального приближения для дальнейшей численной оптимизации, в частности, методом ФО. 

Во втором варианте трассировки рассматриваются лучи, выходящие из точки, вынесенной из фокуса, которые проходят через зеркальную систему и, в конечном итоге, пересекают плоскость апертуры главного зеркала. Этот вариант трассировки традиционно использовался для анализа фазовых аберраций в зеркальных антеннах, как, например, в [11]. Такой вариант удобен при использовании апертурного или токового метода Кирхгофа. Поле на зеркале или в апертуре вычисляется в приближении геометрической оптики (ГО), а затем, в результате интегрирования полученного амплитудно-фазового распределения рассчитывается диаграмма направленности и характеристики сканирования системы [12-14].

В данной работе для анализа аберраций используются первый вариант метода трассировки, а второй вариант используется далее – для оптимизации зеркальной системы с применением токового метода Кирхгофа. В результате оптимизации, как и в работе [15], определяются координаты, угол наклона облучателя, а также ширина диаграммы направленности облучателя при заданном отклонении луча. При полной оптимизации зеркальной системы к этим четырем параметрам добавляются основные геометрические параметры системы: расстояние между зеркалами, положение первичного фокуса и эквивалентное фокусное расстояние (в апланатической системе – фокальный радиус).

 

Геометрия задачи

Рассмотрим двухзеркальную систему, схема которой приведена на рис. 1.

 

 

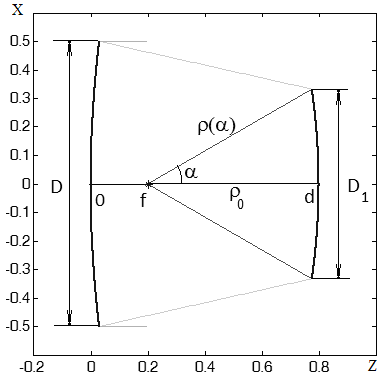
Рис. 1. Продольное сечение двухзеркальной системы.

 

Вершина главного зеркала на рис.1 совмещена с  началом координат декартовой системы X,Y,Z  так, что апертура зеркала параллельна плоскости XOY, ось системы совпадает с осью Z. Обозначим d – расстояние между зеркалами, f  – расстояние от фокуса до главного зеркала на оси системы, - расстояние от фокуса до вспомогательного зеркала, образующая которого описывается из фокуса радиус-вектором . Форма зеркал определяется законом отображения [16,18]. Будем использовать, как и в [18], нормировку геометрических параметров зеркал и величин аберраций за диаметр главного зеркала.

Пусть на главное зеркало под некоторым углом w к оси системы падает пучок параллельных лучей, который в силу осевой симметрии системы без ограничения общности будем полагать параллельным одной из продольных плоскостей, например, XOZ (рис. 2).

 

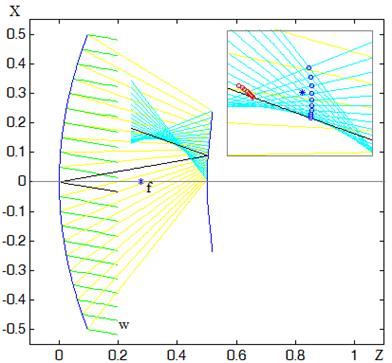
Рис. 2. Трассировка лучей и область фокусировки.

 

Выберем для анализа два семейства лучей: меридиональные лучи, отраженные точками зеркала, лежащими в плоскости XOZ, и сагиттальные лучи, отраженные точками зеркала, лежащими в плоскости YOZ. Луч, отраженный вершиной (центральной точкой) главного зеркала, будем называть главным лучом, а пары лучей, координаты которых на образующих главного зеркала равноудалены от оси Z, – парами зональных лучей.

Рассмотрим пятно рассеяния в области фокусировки в меридиональной плоскости, т.е. в плоскости XOZ (см. рис. 2). Здесь, а также и далее, при иллюстрации лучевой картины в области фокусировки, будем обозначать точки пересечения пар зональных меридиональных лучей кружками синего цвета, а точки пересечения меридиональной плоскости парами зональных сагиттальных лучей – красного. Определим центр пятна в меридиональной плоскости (на рис. 2 обозначен звездочкой) как центр окружности, вписанной в треугольник, стороны которого образованы главным лучом и двумя краевыми меридиональными лучами, а вершины лежат на пересечении этих лучей. Радиус окружности, характеризующий величину поперечных аберраций меридиональных лучей, обозначим как радиус комы d_K, хотя, строго говоря, в этой области присутствует смесь различных видов аберраций высших порядков. Построим плоскость, проходящую через центр пятна рассеяния перпендикулярно главному лучу, и определим пересечение лучей с этой плоскостью как ортогональное сечение пучка. При этом расстояние от точки пересечения парой зональных сагиттальных лучей меридиональной плоскости до данного сечения характеризует продольный астигматизм, а проекция соответствующего отрезка сагиттального луча на ортогональное сечение может быть определена как мера поперечного астигматизма или радиус пятна d_A в сагиттальной плоскости. 

Сравним определенные выше численные характеристики пятна рассеяния с аналитическими зависимостями оптической теории аберраций 3-го порядка. Как следует из оптиической теории аберраций [22], полный размер пятна комы определяется выражением:

                     ,                                                                          (1)

величина астигматизма в классических двухзеркальных системах - выражением:

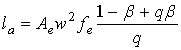                     ,                                                            (2)

а величина астигматизма в апланатических системах - выражением:

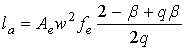                     ,                                                            (3)

где A_e – нормированная апертура, A_e =D/f_e, D – диаметр объектива, f_e – эквивалентное фокусное расстояние, а параметры q, b  записываются в виде:

                       , .                                                              (4)

В апланатической системе величина f_e равна фокальному радиусу f₁, в системе Кассегрена: f_e=F(e+1)/(e-1), где F–фокальное расстояние параболы, e– эксцентриситет гиперболы, определяемые параметрами зеркальной сиcтемы d, r_o. Как следует из оптической теории аберраций, среди апланатических систем астигматизм может быть устранен только в системе Шварцшильда (предфокальной системе), если выполняется условие [22]:

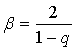                                        .                                                                (5) 

Преобразуем приведенные выше  соотношения (1-3) для классической системы Кассегрена и апланатической системы Шварцшильда c учетом (4) и представим полученные формулы для радиусов комы и астигматизма в таблице 1 (без нормировки величин).

 

Таблица 1. Основные формулы теории аберраций 3-го порядка.

	Система Кассегрена	Система Шварцшильда
Кома
Астигматизм

 

Для дальнейшего сопоставления численных и аналитических величин аберраций выберем продольные размеры систем, по сравнению с поперечными, достаточно большие, например, d=2, r_o =2 и выполним трассировку лучей в системах Кассегрена и Шварцшильда для двух значений угла зрения w=2° и w=20°.

На рис. 3, 4 (кружками) изображены зависимости радиусов d_K (синие кривые) и d_A  (красные кривые) от эквивалентного фокусного расстояния системы Кассегрена  fe  (3а, 4а) и фокального радиуса системы Шварцшильда f₁ (3б, 4б), полученные численно как результат трассировки при w=2° (рис. 3) и w=20° (рис. 4).

 

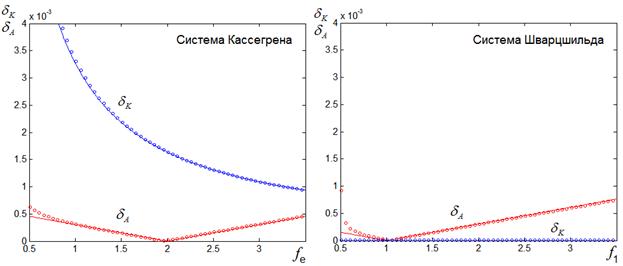
а)   система Кассегрена                      б) система Шварцшильда

Рис.3. Зависимости радиусов пятна от эквивалентного фокусного расстояния   (d=2, r₀=2, w=2°).

 

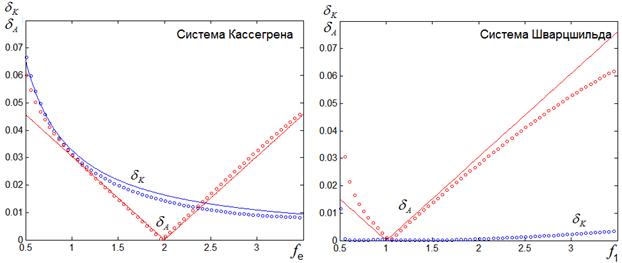
а)   система Кассегрена                          б) система Шварцшильда

Рис.4. Зависимости радиусов пятна от эквивалентного фокусного расстояния  (d=2, r₀=2, w=20°).

 

 На этих же рисунках сплошными кривыми изображены аналитические зависимости, соответствующие формулам оптической теории аберраций 3-его порядка, приведенным выше в таблице.

В соответствии с рис. 3 при угле зрения w=2° численные и аналитические зависимости практически совпадают. При угле зрения w=20° (см. рис. 4) также имеется достаточно хорошее совпадение, особенно в области минимума d_A. Мы видим, что в этой области параметров справедливы условия отсутствия астигматизма в двухзеркальных системах, следующее из теории аберраций 3-его порядка (см. таблицу): d = fe  – в системе Кассегрена , d=2 f₁  – в системе Шварцшильда.

Выполнение указанных условий для классической и апланатической системы иллюстрируются, соответственно, на рис. 5, 6. На рисунках представлены лучевые картины в пятнах рассеяния при трассировке лучей для угла зрения w=2°. Точки пересечения зональных меридиональных лучей, как и ранее на рис. 3, изображены синим цветом, сагиттальных лучей – красным.

На рис.5а (fe=f₁=2) показан ход лучей в классической системе с устраненным астигматизмом, а на рис. 6б (fe=f₁=1) – в апланатической системе с устраненным астигматизмом.

         Используем далее предложенные характеристики для анализа аберрации в системах с малыми продольными размерами, например –  d=0.6, r₀=0.3,   при угле зрения w=20°.

 

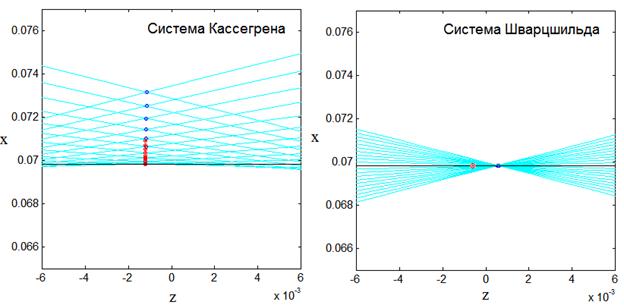
а)   система Кассегрена  (анастигмат)                б) система Шварцшильда

Рис.5. Области фокусировки в двухзеркальных системах с параметрами:

r₀=2.0,  fe = f₁ =d=2.0 при  угле зрения w=2°.

 

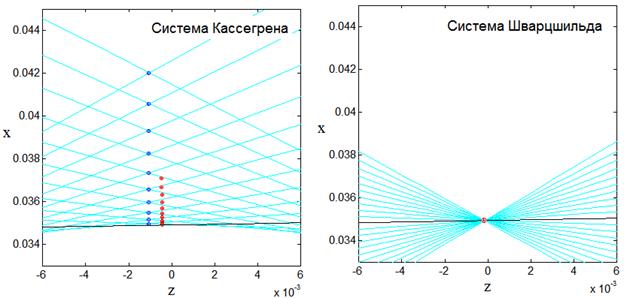
а)   система Кассегрена             б) система Шварцшильда (анастигмат)

Рис.6. Области фокусировки в двухзеркальных системах с параметрами: r₀=2.0 d=2.0, fe = f₁ =d/2=1 при  угле зрения w=2°.

 

Зависимости радиусов пятен рассеяния d_K и d_A  от эквивалентного фокусного расстояния f_e, полученные в результате трассировки лучей в системах Кассегрена и Шварцшильда, представлены, соответственно, на рис. 7а и 7б.

 

    а)  Система Кассегрена                    б)   Система Шварцшильда

Рис.7. Зависимости радиусов пятна рассеяния от эквивалентного фокусного расстояния  (d=0.6, r₀ =0.3, w=20°).

 

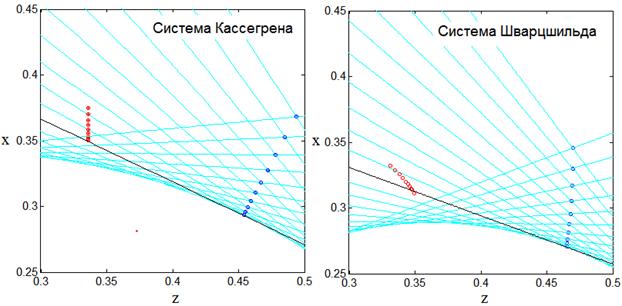
a)  Система Кассегрена                     б) Система Шварцшильда

Рис.8. Области фокусировки двухзеркальных систем с параметрами:

d=0.6, r₀ =0.3, f₁  =1, w=20°.

 

Обозначения и цвет кривых на этих рисунках –  такие же, как и на рисунках 4, 5: синие кривые – d_K, красные кривые – d_A, сплошные линии соответствуют теории аберраций, кривые с кружочками – результат трассировки. Пятна рассеяния, иллюстрирующие вид аберраций в этих системах при значении  fe=f₁=1, изображены на рис. 8.

Из анализа лучевой картины на рис.7 видно, что в применение формул теории аберраций 3 порядка в данном примере приводит к ошибкам. При этом  условие устранения астигматизма зависит от зоны на главном зеркале (рис. 8) и в рассматриваемой области астигматизм не может быть  устранен одновременно для всех зональных лучей. Величина комы высшего порядка для системы Шварцшильда в данной области параметров значительна и соизмерима с величиной комы в системе Кассегрена. В соответствии с рис.7 минимальные аберрации в апланатических системах с небольшими расстояниями между зеркалами обеспечиваются при фокальном радиусе, приближающемся к своему предельному значению f₁=0.5. Этот результат объясняет малые секторы сканирования зеркальных антенн (несколько градусов), полученные в работах [12-15] при исследовании апланатических систем с малыми продольными размерами  и большими значениями фокального радиуса f₁  ³1. 

Дальнейшее исследование апланатической системы Шварцшильда с целью минимизации аберраций будем проводить для сагиттальных и  меридиональных лучей с использованием предложенных выше численных характеристик аберраций (соответственно, для анализа астигматизма и поперечных аберраций в виде комы). При наличии аберраций высших порядков полная картина аберраций весьма сложная, в ней могут присутствовать такие аберрации меридиональных лучей как кома 5-го и 7-го порядка, боковая сферическая аберрация и т.д. [22,23]. Об этом говорит вид пятна рассеяния в меридиональной плоскости, когда точки пересечения зональных лучей могут образовывать траекторию, пересекающую главный луч, вообще говоря, не один раз. Предложенные  выше характеристики для оценки аберраций меридиональных лучей позволяют описывать лишь поперечные аберрации и не учитывают продольную сферическую аберрацию. Следует также заметить, что при исследовании мы не принимаем во внимание затенение вспомогательным зеркалом, размеры которого могут быть весьма значительными именно в тех областях, где меридиональные аберрации минимальны [18]. Результаты исследования без учета затенения показывают лишь потенциальные возможности осесимметричной  системы Шварцшильда.

При анализе аберраций будем  в дальнейшем дополнительно нормировать радиусы пятна рассеяния на фокальный радиус системы f₁ . Такая нормировка позволяет при сравнении геометрооптического и дифракционного радиусов пятна непосредственно на графиках зависимостей определять допустимый электрический размер зеркала.

 

Аберрации сагиттальных лучей

Рассмотрим характеристики астигматизма, полученные в результате трассировки лучей в зеркальной системе Шварцшильда при изменении параметров зеркал d, r₀ , f₁  и угла падения лучей w. Важной характеристикой является зависимость d_A / f₁  от f₁ , которая определяет условие минимизации астигматизма при изменении параметров d, r₀ ,w, а также  R - радиуса зоны главного зеркала.

На рисунках 9, 10 приведены графики зависимости нормированной величины d_A / f₁  (ее десятичного логарифма) от фокального радиуса f₁  системы при расстоянии между зеркалами d=1.2 и угле зрения w=25°.

На рис. 9 представлено семейство кривых, полученных для краевого луча при варьировании параметра r₀, на  рис. 10 – семейство кривых при фиксированной величине r₀=0.3, переменным параметром является радиус зоны R .

Минимум радиуса пятна на рис.9 зависит от расстояния r₀, но с увеличением r₀, начиная со значения r₀=0.4, эта зависимость выражена слабо.

 

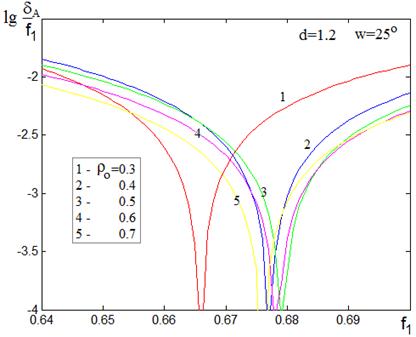
Рис.9. Зависимости величины астигматизма от фокального радиуса  при изменении расстояния r₀.

 

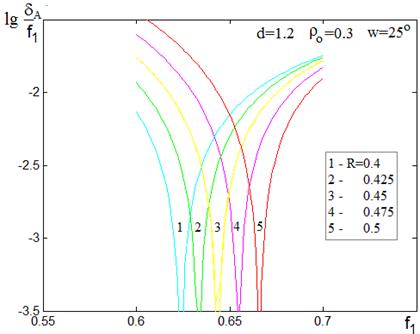
Рис.10. Зависимости величины астигматизма от фокального радиуса  при изменении радиуса зоны R.

 

В соответствии с рис. 10 минимум радиуса пятна зависит от радиуса зоны на главном зеркале. При уменьшении величины R значение фокального радиуса, обеспечивающего этот минимум, уменьшается и для параксиальных лучей приближается к значению 0.6, равному половине расстояния между зеркалами d=1.2. На рисунках 11,12 приведены зависимости величины d_A / f₁   от  фокального радиуса f₁ для краевого луча в системе  с фиксированным значением r₀=0.3. На рис. 11 – семейство кривых при изменении угла зрения w (d=1.2), на рис. 12 – при изменении расстояния между зеркалами d  (w=25°).

В соответствии с рисунками, положение минимумов радиуса пятна существенно зависит и от расстояния между зеркалами d, и от угла зрения w.

С уменьшением расстояния между зеркалами уменьшается фокальный радиус, требуемый для минимизации астигматизма,  при этом условие  f₁=d/2 не выполняется и для малых углов зрения w. Зависимость минимума радиуса астигматического пятна от угла зрения (что характерно для смешения аберраций 3-го и 5-го порядка) говорит о том, что для каждого угла зрения для минимизации астигматизма существует свой оптимальный фокальный радиус.

Из проведенного анализа следует, что в зеркальных системах с малыми продольными размерами величина астигматического радиуса пятна рассеяния, а также условие минимизации астигматизма зависят практически от всех параметров системы. При этом оптимальный фокальный радиус слабее зависит от r₀, чем от остальных параметров.

 

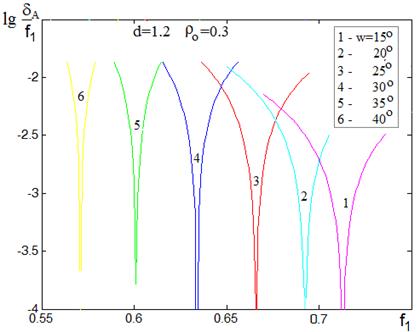
Рис.11. Зависимости величины астигматизма от фокального радиуса при изменении угла зрения.

 

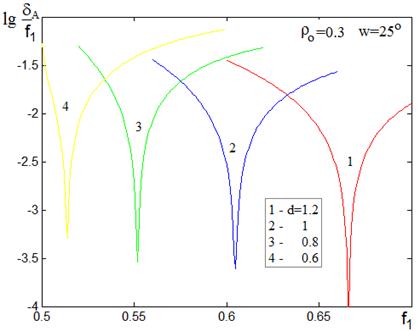
Рис.12. Зависимости величины астигматизма от фокального радиуса при изменении  расстояния между зеркалами.

 

Аберрации меридиональных лучей

Рассмотрим теперь характеристики аберраций меридиональных лучей. Воспользуемся при этом результатами минимизации несимметричных поперечных аберраций, полученными в работе [18] для планарных двумерных апланатических зеркальных систем по критерию среднеквадратичной аберрации (СКА). Величина СКА в данной работе была определена как среднеквадратичное отклонение s точек пересечения пар зональных меридиональных лучей от главного луча. Минимизированные значения СКА представлены на рис. 13а в виде распределений нормированной величины s/f₁  в области изменения параметров зеркал d и r₀, а соответствующие им значения фокального радиуса, обеспечивающие минимальные значения  s/f₁  для каждой пары величин d и r₀, – на рис. 13б. Расчеты проведены для угла зрения w=20°. Как было показано в [18], c увеличением угла зрения w величина s/f₁ в областях, характеризующихся минимальными аберрациями, растет почти пропорционально w³, при этом вид распределения s/f₁ в зависимости от d,r₀ практически не меняется. На рис. 13а в области d>0.6, r₀>0.6 мы видим глубокий минимум аберраций (в соответствии со шкалой уровня lg(s/f₁) – синего цвета). Эта область характеризуется линейной зависимостью r₀ от d и положением фокуса за главным зеркалом (f<0). Важная особенность этой области  – большой размер вспомогательного зеркала. Еще одна область с минимальными аберрациями, как было показано в работе [18], наблюдается в системах с малыми расстояниями между зеркалами d<0.2 при r₀ >0.8. В этой области была реализована широкоугольная планарная система [19] с равными размерами главного и вспомогательного зеркал. Следует заметить, что полученные в [18] зависимости между параметрами зеркал, характеризующие минимальные аберрации, противоречат приведенным в [17] рекомендациям: .

 

а)                                                              б)

Рис.13. Распределение минимальных среднеквадратичных аберраций меридиональных лучей
и соответствующих значений оптимального фокального радиуса.

Области r₀<0.5 (на рис.13а – красного цвета) соответствуют большие аберрации. Как следует из расчетов, поперечные меридиональные аберрации в этой области растут с уменьшением расстояния от фокуса до вспомогательного зеркала r₀, тогда как в приближении теории аберраций 3-го порядка радиус комы не зависит от этой величины. Как показывают расчеты [18], в данной области можно реализовать приемлемое затенение вспомогательным зеркалом, но небольшие углы зрения w.

Дальнейший анализ аберраций будем проводить без учета размеров вспомогательного зеркала, при этом будем помнить о влиянии этого фактора при выборе схемы и параметров оптимальной системы.

 

Алгоритм анализа и минимизации аберраций

Представим на одном рисунке (рис. 14) зависимости величин ,  и  от фокального радиуса f₁, полученные при трассировке лучей при изменении расстояния между зеркалами d=0.6; 1.0; 1.8; 2.6 для фиксированных значений r₀=0.3, R=0.5, w=25°.  На графиках кривые зависимостей величин  s, d_K и d_A  изображены, соответственно, зеленым, синим и красным цветами.

 

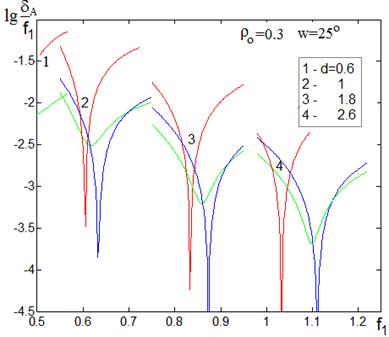
Рис.14. Зависимости аберраций меридиональных и сагиттальных лучей

 от фокального радиуса и расстояния между зеркалами.

 

В соответствии с рисунком все кривые семейств имеют заметные минимумы. Положения минимумов величин, характеризующих меридиональные аберрации d_K и s, близки между собой, минимум среднеквадратичной аберрации s смещен в сторону меньших значений f₁. Тот факт, что в области минимумов d_A  кривые s меняются медленно, позволяет на начальном этапе оптимизации минимизировать d_A. При этом алгоритм анализа и минимизации аберраций  заключается в следующем. При заданном угле зрения w для каждого расстояния между зеркалами d определяем значение фокального радиуса f₁opt, при котором наблюдается минимум величины d_A, при этом астигматизм устраняется для некоторого зонального луча, в данном случае (рис.14) – краевого. Далее, при найденном значении фокального радиуса f₁opt,  определяем величину , характеризующую усредненные меридиональные аберрации. Требуя, чтобы среднеквадратичный размер геометрооптического сечения пятна s был меньше дифракционного радиуса пятна Эйри , можно оценить допустимый  электрический размер главного зеркала .

Семейства кривых, изображенные на рис. 15, позволяют проанализировать зависимость уровня аберраций в системах с оптимальными значениями фокального радиуса от расстояния между зеркалами. В соответствии с рисунком при уменьшении расстояния между зеркалами d значения s/ f₁  в области минимумов  d_A /f₁   увеличиваются.

Рассмотрим в качестве примеров для анализа четыре апланатические системы с параметрами:

  1) d=1.2, r₀ =0.3;

  2) d=0.6, r₀ =0.6;

  3) d=0.9, r₀ =0.96.

 4) d=0.868, r₀ =0.165, f₁ =0.5797.

 Система (1) характеризуется маленьким расстоянием от фокуса до вспомогательного зеркала. Система (2) характеризуются в [17] как лучший апланат, обеспечивающий сектор сканирования ±45° даже при значительных электрических размерах главного зеркала. Параметры системы (3) соответствуют области минимума меридиональных аберраций (рис. 13). Система (4) предложена для использования в γ-телескопе, обеспечивающем поле зрения 2w=8°  при диаметре главного зеркала D=9.66 м [10,11].

 Значения фокальных радиусов f₁opt, полученные при минимизации астигматизма краевых лучей для первых трех систем, равны, соответственно, 0.67, 0.514, 0.58. Трассировка лучей в этих системах изображена на рисунках 15-17.

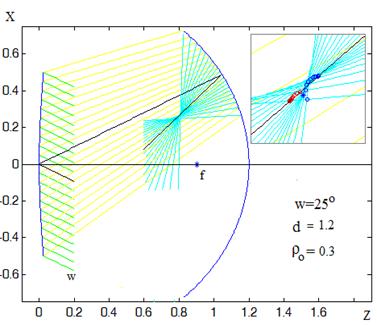
Рис.15. Фокусировка в системе (1) при устраненном астигматизме краевого луча.

 

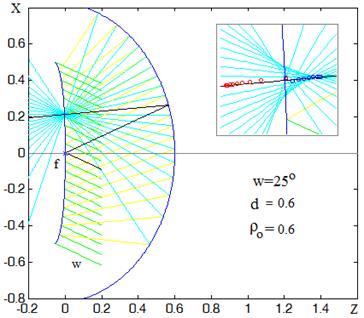
Рис.16. Фокусировка в системе (2) при устраненном астигматизме краевого луча.

 

Рис.17. Фокусировка в системе (3) при устраненном астигматизме краевого луча.

 

Увеличенные фрагменты области фокусировки на этих рисунках иллюстрируют вид существующих аберраций. Заметим, что точки пересечения меридиональных и сагиттальных зональных лучей сближаются с ростом радиуса зоны, максимальный астигматизм наблюдается для параксиальных лучей. Для краевых сагиттальных лучей астигматизм устранен, так как их точка пересечения лежит в плоскости сечения, проходящего через центр пятна, изображенного на рисунках звездочкой.

Трассировка лучей в четвертой системе и увеличенная область фокусировки, иллюстрирующие вид существующих аберраций,  изображены на рис.18.

Определим оптимальный фокальный радиус в системе Шварцшильда с параметрами d=0.868, r₀ =0.165 по зависимости величины lg(d_A/f₁) от фокального радиуса f₁. Эта зависимость, полученная в результате трассировки лучей при w=4° и радиусе зоны R=0.4, приведена на рис. 19 кривой красного цвета, зеленая кривая характеризует среднеквадратичные аберрации меридиональных лучей. Обоснованность выбора значения  радиуса зоны будет дана ниже. В соответствии с рисунком при значении фокального радиуса f₁opt=0.5797 наблюдается минимум величины lg(d_A/f₁), что совпадает со значением фокального радиуса f₁ =0.5797, характеризующего телескоп, оптимизированный с использованием программ оптического проектирования в [10].

 

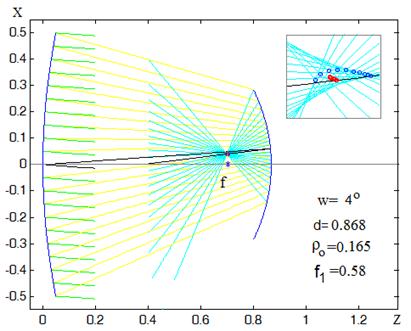
Рис.18. Система Шварцшильда–Кудэ [10].

 

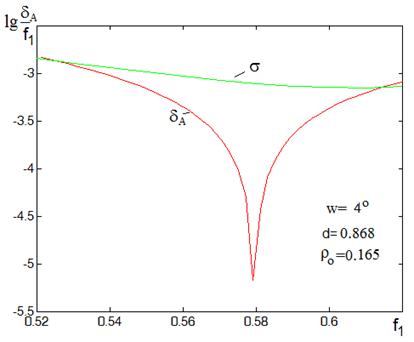
Рис.19. Минимизация астигматизма в системе Шварцшильда-Кудэ.

Оптимизация зеркальной системы в приближении ФО

Проведем проверку эффективности предложенного геометрооптического алгоритма анализа и минимизации аберраций методом ФО. Выберем в качестве основного параметра, характеризующего эффективность сканирования зеркальной системы, величину КИП при заданном угле отклонения луча. Вычисления КИП были проведены с использованием токового метода Кирхгофа и модели облучателя в виде скалярного рупора [15]. Для заданного угла отклонения луча при вычислениях оптимизировались величины поперечного и продольного смещений d_x, d_z облучателя из фокуса системы, а также угол наклона оси облучателя d_b. Кроме этого, при оптимизации определялись также значения фокального радиуса и ширина диаграммы облучателя.

Исследуем зависимости КИПа от расстояния между зеркалами d для систем с параметром r₀=0.3  при фиксированном угле зрения w=25° Соответствующие этому случаю характеристики аберраций были рассмотрены ранее (рис. 14). На рис. 20 приведены результаты вычислений КИПа при изменении расстояния между зеркалами d в диапазоне от 0.6 до 1.2 для различных значений электрического размера зеркала D/l=20, 50, 100  (кривые зеленого, красного и синего цвета, соответственно).

 

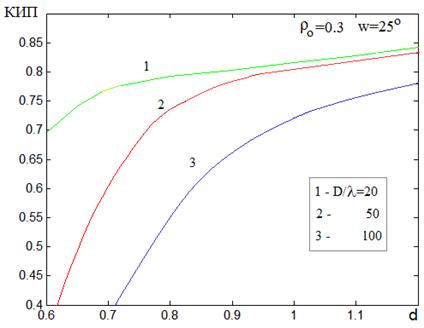
Рис. 20. Зависимости КИП от расстояния между зеркалами.

 

Зависимость фокального радиуса f₁opt от величины d, полученная в результате оптимизации, изображена на рис. 21 (кривая 4 красного цвета).

 

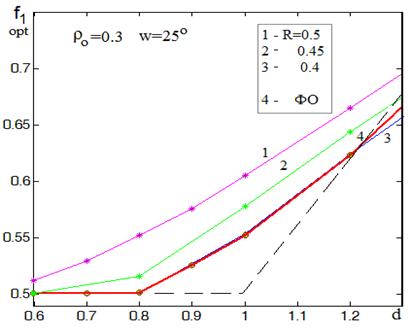
Рис.21. Зависимости оптимального фокального радиуса от расстояния между зеркалами.

 

На этом же рисунке для сравнения представлены полученные при трассировке зависимости фокального радиуса, обеспечивающего устранение астигматизма для зональных лучей: кривая 1 – для краевых лучей (R=0.5), кривые 2,3 – для зон главного зеркала с радиусами R=0.45 и R=0.4, соответственно. Пунктирная линия черного цвета соответствует условию Кудэ f₁=d/2.      

  В соответствии с рис.21 зависимости для фокального радиуса, полученные при оптимизации методом ФО, практически совпадают с зависимостями, полученными в результате трассировки лучей из зоны с радиусом R=0.4 (кривая 3 синего цвета). Это можно объяснить следующим образом. Амплитудное распределение, как правило, спадает к краям зеркала, при этом уровень облучения кромки главного зеркала составляет -10 дБ и менее. Это фактически означает уменьшение влияния на КИП краевых зональных лучей. С другой стороны их влияние растет, так как с увеличением радиуса зоны растет площадь колец. В результате для облучателя в виде гофрированного рупора мы имеем значение R=0.4, полученное ранее при определении фокального радиуса, обеспечивающего минимизацию астигматизма системы (4). Это значение будет использоваться и далее для корректного определения оптимального фокального радиуса системы при трассировке лучей.

На рис. 22 приведены характеристики сканирования (зависимости КИПа от угла отклонения луча), полученные при D/l=50 методом ФО в результате оптимизации систем (1) – (3). Значения оптимальных фокальных радиусов f₁  в этих системах: 0.63, 0.53 и 0.5, соответственно, были определены в результате трассировки лучей для угла зрения w=25° при радиусе зоны краевого луча R=0.4.

Как следует из вычислений, система (1) имеет характеристику сканирования вида, характерного для бифокальных систем, при этом поле зрения (ширина сектора сканирования по уровню КИП=0.5) достигает 70°. Система (2) при D/l=50 имеет поле зрения 52°, хотя была предложена в [17] как 90-градусный апланат. Поле зрения в этой системе ограничено из-за значительной величины астигматизма. Отметим, что размеры вспомогательного зеркала в этих двух системах примерно одинаковы.

 

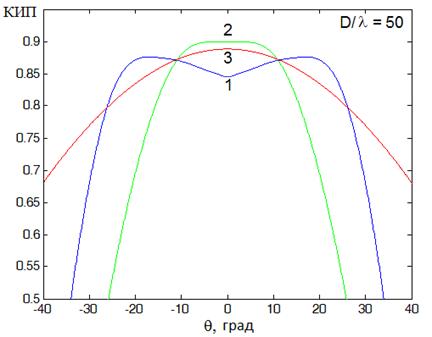
Рис.22. Характеристики сканирования систем (1), (2), (3) с параметрами:

1– d=1.2, r₀ =0.3,  f₁=0.62;       2 – d=0.6, r₀ =0.6,  f₁=0.5;

3 – d=0.9, r₀ =0.96,  f₁=0.5.

 

Система (3), в которой минимизированы аберрации и меридиональных, и сагиттальных лучей, при данном электрическом размере зеркала в секторе углов ± 40 градусов является практически безаберрационной. При этом КИП на краю этого сектора равен 0.68 и определяется только уменьшением эквивалентной апертуры.

Полученные при трассировке такие характеристики пятна рассеяния, как координаты центра пятна рассеяния, угол наклона главного луча и угол между краевыми лучами в пятне рассеяния использовались как начальные значения для параметров, определяемых при оптимизации: поперечного и продольного смещения, угла наклона оси облучателя, а также его ширины диаграммы направленности. Как показали расчеты, эти данные определяются с высокой точностью, и их использование существенно сокращает время дальнейшей оптимизации и получения характеристик сканирования. На рис. 23, на примере системы (1), приведены для сравнения фокальные кривые, полученные в результате трассировки лучей и при оптимизации методом ФО.

 

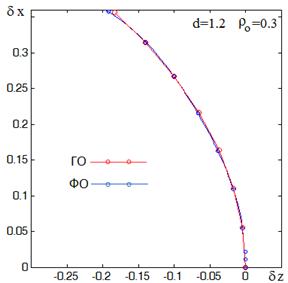
Рис.23. Продольное и поперечное смещение источника из фокуса (фокальные кривые).

 На рис. 24 представлены соответствующие зависимости угла поворота облучателя от угла сканирования. Как видно из сравнения, наблюдается практическое совпадение кривых.

 

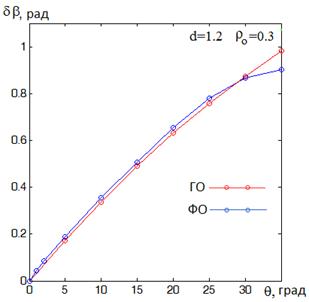
Рис.24. Угол поворота облучателя в зависимости от угла сканирования.

 

Рис.25. Характеристики сканирования в системе с параметрами

  d=1.2, r₀ =0.3, оптимальные для различных секторов обзора.

Следует добавить, что из-за зависимости величины оптимального фокального радиуса от угла зрения при минимизации астигматизма можно получить различные характеристикам сканирования, задавая различные значения угла w при оптимизации. В качестве иллюстрации на рис. 25 приведены две характеристики сканирования, полученные для зеркальных систем  с параметрами d=1.2, r₀ =0.3. Этим характеристикам соответствуют различные значения фокального радиуса, фокальные кривые и оптимальные параметры облучателя, полученные при начальной оптимизации для разных углов зрения (кривая 1– w=25° , кривая 2– w=35°).

 

Выводы

– Введение численных характеристик пятна рассеяния в области фокусировки позволяет получить зависимости величин аберраций от геометрических параметров двухзеркальных систем для произвольных углов зрения.

– При больших углах зрения величина комы высшего порядка в апланатической системе может быть сравнима с величиной комы в классической системе с эквивалентными параметрами.

–  При больших углах зрения устранение астигматизма в двухзеркальных системах невозможно одновременно для всех зональных лучей. При стандартном облучателе оптимальный радиус зоны на главном зеркале для устранения астигматизма равен 0.8 радиуса апертуры.

–  Численные параметры аберраций в области фокусировки, определяемые по предложенному алгоритму (центр пятна рассеяния, угол наклона главного луча, угол между краевыми лучами), с большой точностью позволяют находить положение и угол наклона облучателя, что, в свою очередь, позволяет их использовать в качестве начального приближения при численной оптимизации двухзеркальной системы.

– Требования широкоугольности зеркальной системы и минимального затенения излучения вспомогательным зеркалом в осесимметричной системе Шварцшильда находятся в противоречии. Областям с малыми аберрациями соответствуют размеры вспомогательного зеркала, соизмеримые с размером главного зеркала или даже превышающие его.

 

Литература

1.     K. Schwarzschild. K. Schwarzschild, 1905. Astronomische Mittheilungen der Koniglichen Sternwarte zu Gottingen 10, 3 (Part II). Reprinted: Selected Papers on Astronomical Optics, D.J. Schroeder (ed.), SPIE Milestone Series 73, 3, 1993.

2.     A. Couder. Compt. Rend. Acad. Sci., Paris, 1926.1276H. Chreґ tien, Rev. d’Opt. 1, 13, 49, 1922.

3.     H.Chritien, Rev. d'Opt.1,13,49,1922.

4.     Максутов Д.Д., Тр. ГОИ 8, №86, 1932.

5.     W.B. Wetherell, M.P. Rimmer, General Analysis of Aplanatic Cassegrain, Gregorian, and Schwarzschild Telescopes, Applied Optics, Vol. 11 Issue 12, 1972, pp. 2817-2832.

6.     Charles L Wyman, D. Korsch,  Aplanatic Two-Mirror Telescopes; a Systematic Study. 3: The Schwarzschild-Couder Configuration, Applied Optics, Vol. 14 Issue 4, 1975, pp.992-995.

7.     R.V. Willstrop, The Couder telescope – better than the Schmidt? Mon. Not. Royal Astronomical Society, 1983, June, pp. 99-103.

8.     Теребиж В. Ю., Двухзеркальные апланаты Шварцшильда. Основные  соотношения. Письма в астрономический журнал, 2005, том 31,№2, с. 143–153.

9.     Vassiliev, V. V. and Fegan, S. J., “Schwarzschild-Couder two-mirror telescope for ground-based gamma-ray astronomy”, International Cosmic Ray Conference, 3,1445–1448; arXiv:0708.2741, 2008.

10.  J. Rousselle, V. Connaughton, M. Errando,  Schwarzschild-Couder telescope for the Cherenkov Telescope Array: Development of the Optical System. 33^rd International Cosmic Ray Conference.The Astroparticle Physics Conference, Rio De Janeiro, 2013.

11.  W. White,  L. DeSize,  Scanning characteristics of two-reflector antenna systems, IRE International Convention Record, V.10, Part: 1, 1962 , pp. 44 – 70. 

12.  P.M.J. Scheeren, M.H.A.J. Herben,  E.J.Maanders, Scan Properties of the Schwarzschild Antenna, 11th European Microwave Conference, 1981 , pp.561-566.

13.   M.H.A.J. Herben, J.H.A.W. van de Sande,  P.M.J. Scheeren,  E.J. Maanders, Geometrical optical characteristics of the Scwarzschild scanning antenna. Comparison with the Cassegrain antenna,  Microwaves, Optics and Antennas, IEE Proceedings H, Volume: 129 , Issue: 6 ,1982 , pp.315 – 320.

14.   C.Granet, Designing Schwarzschild dual-reflector systems, Antennas and Propagation Magazine, IEEE, Volume: 48, Issue: 3, 2006, pp. 68 – 74.

15.   Калошин В.А., Фролова Е.В. Характеристики  осесимметричных двухзеркальных апланатических антенн, Антенны, 2006, №7, С.45-51.

16.   Бахрах Л.Д., Галимов Г.К., Зеркальные сканирующие антенны. Теория и методы расчета. М. Наука, 1981, 303с.

17.   Галимов Г.К. Апланаты, т.3, Апланатические телескопы и антенны: “Антенны-связь НПК”, 2011, 436с.

18.   Калошин В.А., Фролова Е.А, Метод анализа и минимизации аберраций в многолучевых планарных зеркальных системах, Журнал радиоэлектроники [электронный журнал.  2014. №1, Режим доступа: http://jre.cplire.ru/jre/jan14/16/text.html/.

19.   Банков С.Е., Грачев Г.Г., Фролова Е.В, Проектирование и экспериментальное исследование планарной многолучевой двухзеркальной апланатической системы, Труды II Всеросc. Микроволной конф., ноябрь 2014., М. ИРЭ им. Котельникова РАН.

20.   Венецкий А.С., Калошин В.А., О распределении эйконала в апертуре двухзеркальной телескопической системы // РЭ, 2012,т.57, №9, с.1004-1011.

21.    Венецкий А.С., Калошин В.А., Аберрации эйконала в планарных двухзеркальных антеннах // РЭ, 2014,т.59, № 10, 1102- 1110.

22.   Михельсон Н.Н., Оптические телескопы: Теория и конструкция, М. Наука 1976, 510с.

23.   Дубовик А.С., Апенко М.И., Дурейко Г.В. и др., Прикладная оптика. М. Недра, 1982, 612с.