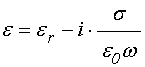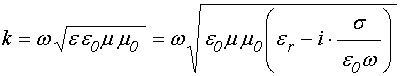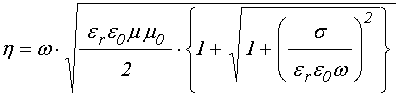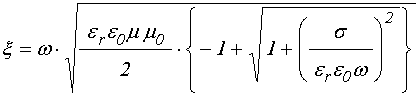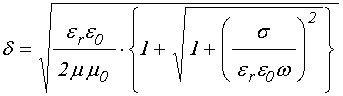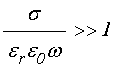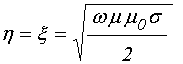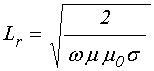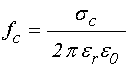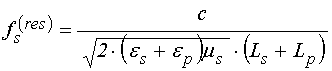УДК 537.874; 537.624

ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ АМПЛИТУД ВНЕШНИХ И ВНУТРЕННИХ ВОЛН В ОГРАНИЧЕННОЙ МНОГОСЛОЙНОЙ СТРУКТУРЕ С ПЕРИОДИЧЕСКОЙ НЕОДНОРОДНОСТЬЮ

ЧАСТЬ 4. ВОЛНА В ДИССИПАТИВНОЙ СРЕДЕ

 

И. В. Антонец ¹, В. Г. Шавров ², В. И. Щеглов²

 

¹ Сыктывкарский государственный университет, Сыктывкар, Россия

² Институт радиотехники и электроники РАН, Москва, Россия

 

Статья получена 3 марта 2015 г.

 

Аннотация. Методом пошагового алгоритма рассмотрено распространение одномерных и электромагнитных волн в многослойной структуре с периодической неоднородностью. Рассмотрено распределение амплитуд волн в слоях структуры. Обнаружен новый вид распределения – линейно-синусоидальный, обусловленный диссипацией среды. Найдено критическое значение проводимости, определяющее переход свойств структуры от диэлектрических к металлическим. Выполнено сравнение эффективности механизмов диссипации для одномерной и электромагнитной волны. Выявлена роль диссипации в формировании дискретного характера амплитудно-частотных характеристик отражения и прохождения. Обнаружен обусловленный проводимостью диссипативный резонанс, а также превышение потока энергии отраженной волны по сравнению с падающей, подобное наблюдавшемуся ранее для двухслойной структуры. В качестве возможного механизма превышения указана локализация энергии во внутренних слоях структуры в виде совокупности активной и реактивной составляющих. Показано, что в случае металлической проводимости необходимым условием синусоидального распределения является  превышение глубины проникновения волны над толщиной барьера. 

Ключевые слова: распространение волн, периодическая структура, частотный спектр, диссипативная среда. 

Abstract. The method the one-dimensional and electromagnetic waves propagation in multi-layer structure with periodical nonuniformity is investigated by successive steps algorithm. The distribution of wave amplitudes inside the layers of structure is considered. The new form of distribution – linear-sinusoidal – which depends on medium dissipation is found. The critical value of electrical conductivity which determines the transition of structure from dielectric to metal properties is found. The comparison of effectiveness of dissipation mechanism for one-dimensional and electromagnetic waves is made. The role of dissipation in formation of discrete character of amplitude-frequency characteristics for reflection and passing of waves is found. The dissipative resonance which is due to conductivity and the exceeding of energy flow of reflected wave compared with falling wave, as it was observed early for two-layer structure, are found. As the possible mechanism for such exceeding the energy localization in the inner slides of structure in the form of active and reactive components is proposed. It is shown that in the case of metal conductivity the necessary condition of sinusoidal distribution is the exceeding the penetration length under the barrier thickness.

Key words: wave propagation, multi-layer structure, periodical nonuniformity, frequency spectrum, dissipative medium.

 

Введение

В предыдущих частях настоящей работы [1-3] было рассмотрено пространственное распределение амплитуд внешних и внутренних волн прямого и обратного направлений в ограниченной многослойной структуре с периодической неоднородностью меандрового вида. В качестве инструмента исследования был использован пошаговый алгоритм [4-7], позволяющий удобным путем как получать аналитические выражения для амплитуд волн, так и рассчитывать распределение этих амплитуд численно. 

Первая часть работы [1] была посвящена одномерным волнам, являющимся элементарным аналогом многих типов волн в различных средах. Введен эквивалент периодической многослойной среды как структуры, состоящей из одинаковых барьеров, разделенных одинаковыми промежутками. Были рассмотрены особенности распространения волн, связанные с периодичностью структуры, исследованы амплитуды волн прямого и обратного направлений, в том числе при большом изменении соотношения между волновыми числами сред, составляющих структуру. Исследована пространственная модуляция амплитуды, выявлены пять основных режимов: синусоидальный, полусинусоидальный, линейный, экспоненциальный, а также синусоидальный с верхним пределом.

Во второй части работы [2] проведенные исследования были обобщены на случай электромагнитных волн. Пошаговый алгоритм видоизменен применительно к ситуации волн, распространяющихся в структуре, свойства которой определяются электродинамическими адмиттансами составляющих ее сред. В широком диапазоне изменения диэлектрической проницаемости сред исследованы частотные зависимости амплитуд волн прямого и обратного  направлений. Относительно распределения амплитуд во внутренних слоях структуры, выявлены два главных его вида – синусоидальное и экспоненциальное. Введены понятия сильной и слабой неоднородностей и получен критерий перехода между ними.  Рассмотрена трансформация частотных зависимостей в широком интервале изменения соотношения проницаемостей слоев.

Третья часть работы [3] посвящена расширению результатов части второй на случай магнитных сред. Было показано, что в такой среде возможно распространение двух  независимых волн – гиромагнитной и гироэлектрической. Рассмотрено отражение и прохождение гиромагнитной волны при падении на плоскую границу раздела двух сред с магнитными параметрами. Получены амплитуды отраженной и проходящей волн, выраженные через адмиттансы сред. Введен в рассмотрение «параметр расходимости», представляющий собой комбинацию из компонент тензора магнитной проницаемости. Показано, что в случае отрицательного знака параметра расходимости распространение гиромагнитной волны невозможно. Рассмотрен баланс потоков энергии распространяющихся волн на структуре в целом. В широком диапазоне рассмотрена частотная зависимость амплитуд волн обоих направлений. В спектре распространения выявлено появление широкой линии, обусловленной магнитными свойствами среды.

В первой и второй частях работы среды, составляющие структуру, полагались бездиссипативными. Магнитная среда, рассмотренная в третьей части, обладала затуханием, феноменологически описываемым механизмом Гильберта [8-11]. Однако было показано, что в случае многослойной среды формальное введение такого затухания не приводит к пространственному уменьшению амплитуды волны в целом, то есть в подобной ситуации гильбертово затухание не является активным, а обладает лишь реактивным характером. Там же было указано на ограничение такого подхода и отмечены условия его применимости. 

С другой стороны, многие реальные среды (полупроводники, электролиты, металлы) в той или иной степени обладают электрической проводимостью, которая неизбежно приводит к активной диссипации энергии волны.

Поэтому настоящая работа посвящена рассмотрению распространения электромагнитных волн в средах, где диссипация обусловлена именно проводимостью. В качестве объекта для сравнения выбрана одномерная волна, позволяющая рассмотреть некоторые явления в более элементарном виде.

1. Геометрия задачи

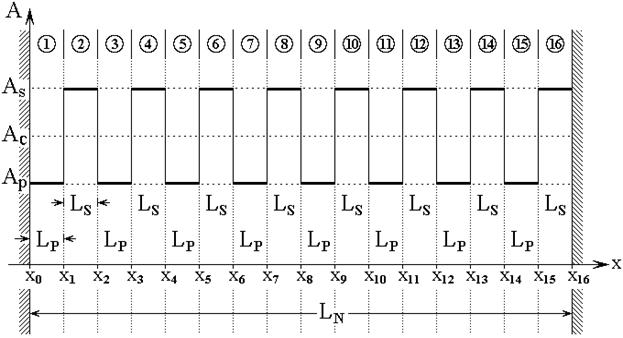
Геометрия задачи совпадает с приведенной в первых трех частях настоящей работы [1-3]. Ее схема показана на рис.1. Рассматривается симметричная меандровая структура, в которой неоднородность представляет собой периодически расположенные одинаковые прямоугольные барьеры, с одинаковыми промежутками между ними. Линейные протяженности барьеров и промежутков равны друг другу.

Структура содержит два вида сред, обозначаемых индексами «» и «», каждый из которых имеет собственные значения параметров. В случае одномерной задачи таковыми являются волновые числа ,  , а в случае электродинамической – диэлектрические ,  и магнитные ,  проницаемости, а также проводимости , . По вертикальной оси отложены значения адмиттансов сред , в случае одномерной задачи их роль играют волновые числа . Остальные обозначения совпадают с приведенными в [1-3].

Число слоев – . Полная длина структуры, кроме особо оговоренных случаев – , толщины слоев – ,

 

Рис.1. Общая схема ограниченной многослойной структуры с периодической неоднородностью симметричного меандрового вида. Цифры в кругах – номера слоев (сред).

 

2. Распределение амплитуд для одномерной волны

    Для того, чтобы выявить основные закономерности распространения волн в периодической структуре с диссипацией, обратимся сначала к случаю одномерной волны, как имеющему более элементарный характер. Для одномерной волны основным фактором ее распространения является волновое число, которое в среде с диссипацией является комплексным, причем спад амплитуды по координате описывается мнимой частью волнового числа.

    Рассмотрим рис.2, где показаны распределения амплитуд волн обоих направлений в многослойной структуре при некоторых характерных значениях комплексного волнового числа.

 

Рис.2. Распределение нормированных амплитуд волн прямого (сплошные линии и сплошные точки) и обратного (пунктирные линии и открытые точки) направлений от координаты при различных значениях  комплексного волнового числа. Волновое число промежутка: .

Волновое число барьера:

а –  ; б–  ;

в –  ; г –  ;

д–  ; е –  ;

 

При построении рисунка значения волновых чисел были подобраны таким образом, чтобы в случаях а,б,в действительная составляющая волнового числа для барьера значительно (в  раза) превышала таковую для промежутка, тогда как в случаях г,д,е действительная составляющая волнового числа для барьера равнялась таковой для промежутка, а волновые числа барьера и промежутка отличались только мнимой составляющей.

Для построения непрерывных кривых на рис.2 использовались следующие эмпирические формулы (с точностью до постоянной составляющей и сдвига фазы): 

а – ; ;                                     (1)

б – ; ;      (2)

в – ;;     (3)

г –  ;  ;                                                                         (4)

д – ;    ;                                           (5)

е – ;;     (6)

Распределение, приведенное на рис.2а, соответствует чисто действительному волновому числу и показано здесь для сравнения.

Распределения, приведенные на рис.2б,д  и 2в,е, соответствуют относительно малой (б,д) и сравнительно большой (в,е) мнимым составляющим волнового числа. 

Распределение, приведенное на рис.2г, соответствуют точному равенству волновых чисел барьера и промежутка при отсутствии мнимой составляющей. То есть неоднородность структуры в целом отсутствует и волна, не испытывая отражения, полностью проходит насквозь.

Распределения, приведенные на рис.2д и 2е соответствуют тем же значениям малой (д) и большой (е) мнимой составляющей волнового числа, что и на рис.2б и 2в, при условии сохранения действительной части волнового числа для барьера равной таковой для промежутка. 

Из рис.2 можно видеть, что в рассматриваемом случае комплексного волнового числа наблюдаются те же основные виды распределения, что и при волновом числе действительном – синусоидальное и экспоненциальное [1]. 

Более точно наблюдаемые распределения можно классифицировать следующим образом (буквы соответствуют эпюрам рисунка):

а – синусоидальное;

б – линейное с добавкой синусоидального, называемое далее линейно-синусоидальным;

в – экспоненциальное;

г – постоянное;

д – для волн прямого направления – линейное, для волн обратного направления – синусоидальное с малой амплитудой; 

е – экспоненциальное для волн обоих направлений.

Отметим некоторые особенности, следующие из общего вида приведенных кривых.

На рис.2а обе синусоиды имеют одинаковый период и одинаковую фазу; средний уровень амплитуды волн прямого направления () выше среднего уровня амплитуды волн обратного направления () примерно в три раза.

На рис.2б коэффициент линейного спада для волн прямого направления () больше коэффициента линейного спада волн обратного направления () примерно в три раза; соотношение средних уровней синусоидальных составляющих амплитуд волн прямого и обратного направлений также около трех раз. Для волн прямого направления  средний уровень вблизи  составляет , амплитуда синусоидальной составляющей – , отношение этих величин равно . Для волн обратного направления  средний уровень вблизи  составляет , амплитуда синусоидальной составляющей – , отношение этих величин равно . Таким образом, для волн прямого направления в распределении преобладает линейная составляющая, для волн обратного направления – преобладает синусоидальная составляющая. 

На рис.2в обе зависимости описываются одной и той же экспонентой, различие состоит только в линейном числовом коэффициенте: для волн обратного направления он составляет  от такого же коэффициента для волн прямого направления.

Подобные особенности наблюдаются и для кривых, приведенных на рис.2г,д,е.

Характерна наблюдаемая при сравнении горизонтальных пар рисунков несколько более слабая зависимость распределений от координаты, свойственная правому столбцу (рис.2г,д,е) по сравнения с левым (рис.2а,б,в). При этом различие между амплитудами волн прямого и обратного направлений при экспоненциальном распределении (рис.2е) составляет около восьми раз, при линейно-синусоидальном (рис.2д) достигает тридцати, а при постоянном (рис.2г) стремится к бесконечности. Можно полагать, что такое отличие обусловлено тем, что для левого столбца в формировании распределений участвуют как действительная, так и мнимая обе составляющие волнового числа, тогда как для правого столбца – только одна мнимая, вклад которой меньше.

3. Роль комплексного характера волнового числа

Рассмотрим теперь специфические особенности приведенных зависимостей, обусловленные именно комплексным характером волнового числа. 

Явное отличие от случая действительного волнового числа здесь состоит в том, что синусоидальное распределение не является самостоятельным, а накладывается на линейное (особенно хорошо это заметно на рис.2б), образуя распределение линейно-синусоидальное.

Наблюдаемое здесь линейное распределение не является переходным от синусоидального к экспоненциальному, а получается как результат убывания амплитуд волн того и другого направлений при удалении их от точки возбуждения (то есть от слоя №1).

Очевидно, такое убывание является следствием затухания волны по координате, что и описывается мнимой составляющей волнового числа. Когда мнимая составляющая становится достаточно большой, линейно-синусоидальное распределение сменяется экспоненциальным, как это видно из рис.2в и 2е. Однако здесь спадающий характер распределения обусловлен не наличием «полос непропускания» при действительном волновом числе, определяемых интерференцией волн при их многократном переотражении [1], а именно затуханием волны по мере ее распространения по координате. 

Это хорошо видно из сравнения рис.2а с рис.2в, где действительная часть волнового числа соответствует области пропускания, а распределение на рис.2в спадает по экспоненте, и особенно из сравнения рис.2г с рис.2д и 2е, где действительная часть волнового числа в переотражении волн вообще не участвует, так как ее значения для барьеров и промежутков между собой равны. Тем не менее, достаточно большая мнимая часть волнового числа и здесь приводит к спаду распределения сначала по линейному закону (рис.2д), а затем по экспоненте (рис.2е).

Таким образом, из проведенного рассмотрения видно, что мнимая часть волнового числа может приводить к таким же видам распределения амплитуд в слоях, что и действительная, однако главная ее роль состоит в уменьшении амплитуд волн по координате по мере удаления от источника возбуждения, которое накладывается на распределения, обусловленные действительной частью волнового числа. 

Замечание.  В проведенном рассмотрении между синусоидальным и экспоненциальным распределениями выделено линейно-синусоидальное, являющееся как бы наложением синусоидального на линейное. Более подробное исследование показывает, что в некоторых случаях подобное наложение синусоидального распределения возможно и на экспоненциальное. То есть на экспоненциальном распределении проявляются следы синусоидального. Однако такое наложение синусоиды на экспоненту является крайне слабым: в исследованных случаях вариации амплитуды за счет синусоиды не превышали нескольких (не более пяти) процентов от амплитуды экспоненты, поэтому в рамках настоящей работы выделение подобного распределения в отдельный вид экспоненциально-синусоидального не проводилось.     

4. Отражающие и пропускающие свойства структуры для одномерной волны

Рассмотрим теперь, какое влияние оказывает затухание волны на отражающие и пропускающие свойства структуры в целом. Как и ранее в качестве наиболее простого примера используем одномерную волну.

 

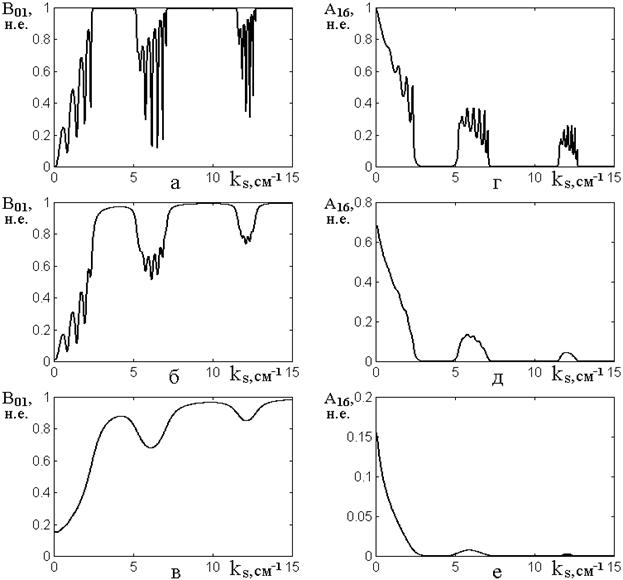
Рис.3. Зависимости амплитуд волн обратного в слое №1 (а,б,в) и прямого в слое №16 (г,д,е) направлений от действительной части волнового числа внутри барьера  при различных значениях его мнимой части. Волновое число промежутка: . Действительная часть волнового числа барьера: . Мнимая часть волнового числа барьера:

а,г –  – затухание отсутствует;  б,д –  – затухание слабое;  в,е –  – затухание сильное.

 

Обратимся к рис.3, где показаны зависимости амплитуд волн обратного в слое №1 (а,б,в) и прямого в слое №16 (г,д,е) направлений от действительной части волнового числа внутри барьера  при различных значениях его мнимой части (для простоты обозначение «» при действительной части волнового числа опущено).     

Рис.3а и 3г соответствуют чисто действительному волновому числу, то есть полному отсутствию затухания. Показанные на них кривые практически тождественны таковым, приведенным в работе [1] на рис.13 и 14, так что представлены здесь для сравнения. 

Рис.3б и 3д соответствуют мнимой добавке к волновому числу равной , то есть, как и в предыдущем разделе,  сравнительно малому затуханию.

Рис.3в и 3е соответствуют мнимой добавке к волновому числу равной , то есть, как и в предыдущем разделе,  затуханию довольно большому.

Из рис.3 видно, что все спектры, на нем представленные, как и в работе [1], имеют дискретную структуру, образованную чередованием областей пропускания и непропускания. При увеличении затухания упомянутые области остаются на своих местах, задаваемых действительной частью волнового числа, то есть их чередующийся характер от величины затухания не зависит. 

При увеличении затухания амплитуда волн того и другого направлений в областях пропускания уменьшается, причем на волнах проходящих (рис.3д,е) такое уменьшение проявляется заметнее, чем на волнах отраженных (рис.3б,в). Так во второй области пропускания (обозначенной в [1] как «1S»), то есть при ) амплитуда отраженных волн в слое №1 в отсутствие затухания (рис.3а) (на уровне максимумов тонкой структуры, считая от верхнего края рисунка) равна , а амплитуда подобных волн при большом затухании (на рис.2в) равна , то есть отношение этих амплитуд составляет . Для проходящих волн в этих же условиях (рис.3в,е)  амплитуды составляют  и , так что их отношение равно . В третьей области пропускания («2S» по [1]), то есть при , амплитуды отраженных волн равны  и , а амплитуды проходящих –  и , то есть их отношения в этом случае составляют  и  соответственно, что превышает подобные отношения для второй области в среднем в два раза.   

Таким образом, как сказано выше, затухание волн обоих направлений, обусловленное мнимой частью волнового числа, сказывается тем сильнее, чем номер области выше. С физической стороны это происходит из-за того, что увеличение номера области означает укладывание большего числа полуволн на длине одного барьера, в результате чего добротность каждого межбарьерного  резонатора падает [12-14] и общее затухание возрастает.

Другой важной особенностью наблюдаемых спектров является тот факт, что на месте исходных областей непропускания (то есть при  – область «1Е» по [1] и  – область «2Е» по [1] ), где в отсутствие затухания волна практически целиком отражается (области экспоненциального распределения амплитуд) при увеличении затухания отражение ухудшается тем более, чем затухание выше (то есть на рис.3б отражение меньше, чем на рис.3а, а на рис.3в – еще меньше). 

Можно полагать, что такое ухудшение отражения при увеличении затухания также обусловлено уменьшением добротности межбарьерных резонаторов, в результате чего их отражающие способности снижаются.

Весьма наглядной особенностью наблюдаемых спектров для волн как отраженных (рис.3а,б,в), так и проходящих (рис.3г,д,е) является происходящее по мере увеличения затухания постепенное уменьшение тонкой структуры резонансных линий, соответствующих областям пропускания, вплоть до полного ее исчезновения (рис.3в, 3е). Такое уменьшение расщепления резонансных линий сходно с расщеплением общей резонансной линии системы двух и более связанных резонаторов, уменьшающимся при увеличении затухания [12-14]. 

Таким образом, из проведенного рассмотрения можно сделать вывод, что при увеличение затухания общая структура спектра, то есть расположение областей пропускания и непропускания по волновому числу в целом не меняется, тогда как прохождение волн и их отражение в соответствующих областях ухудшаются тем сильнее, чем номер области больше, причем тонкое расщепление спектра внутри областей пропускания с увеличением затухания сглаживается.

5. Электромагнитная волна в проводящей среде

Теперь, когда распространение одномерных волн в многослойной структуре с диссипацией в основном рассмотрено, обратимся к более сложному случаю электромагнитных волн.  

Для электромагнитной волны главной причиной диссипации является проводимость среды. Общие принципы введения проводимости в расчетный аппарат пошагового алгоритма рассмотрены в работе [2]. Здесь повторим лишь некоторые необходимые далее основные положения.

Диэлектрическая проницаемость в среде с проводимостью  принимает  вид [15-17]:

,                                                                                   (7)

где  – диэлектрическая проницаемость в отсутствие проводимости, являющаяся действительной. 

    Волновое число, становясь комплексным,  приобретает вид:

.                               (8)

 

Следуя правилам извлечения квадратного корня из комплексного числа [18], получаем: 

,                                                                                           (9)

где:

;                                (10)

.                           (11)

В таком виде волновое число входит в показатели экспонент в выражениях, получающихся в ходе реализации пошагового алгоритма.

Адмиттанс в проводящей среде также становится комплексным:

,                                                                                          (12)

где:

;                                           (13)

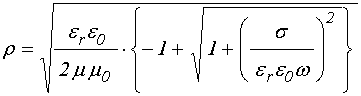.                                        (14)

В таком виде адмиттансы входят в линейные суммы выражений, получающихся в ходе реализации пошагового алгоритма.

Для практики представляет большое значение случай высокой проводимости, какой например, обладают металлы. При этом форма выражений (10)-(11) и (13)-(14) определяется величиной последнего слагаемого под внутренним корнем по сравнению с единицей. Так при выполнении условия:

 ,                                                                                        (15)

 

что может иметь место при высокой проводимости или низкой частоте, действительная и мнимая компоненты волнового числа  и , а также адмиттанса  и , становятся попарно равными друг другу, приобретая вид:

;                                                                           (16)

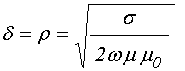.                                                                           (17)

 

Можно видеть, что в обоих случаях зависимость от проводимости имеет корневой характер.

Замечание.  В рассматриваемой здесь задаче о диссипации магнитные свойства вещества не учитываются, то есть магнитная проницаемость, входящая в выражения (8)-(17), полагается равной единице. В работе [3] при рассмотрении магнитной проницаемости в тензорном виде, был сделан вывод об отсутствии  диссипации для структуры в целом, несмотря на учет затухания в магнитной среде с помощью механизма Гильберта [8-11]. Такой результат получен из-за предположения о действительности компонент тензора магнитной проницаемости, представленных в работе [3] в виде формул (108)-(109). В этом случае как волновое число, так и адмиттанс остаются действительными, что и проявляется как отсутствие диссипации, несмотря на наличие гильбертова затухания. 

Для последовательного учета диссипации, обусловленной гильбертовым механизмом, надо учитывать комплексный вид компонент магнитной проницаемости, описываемый в работе [3] формулами (103)-(104). При этом приведенные здесь компоненты волнового числа (10)-(11) и адмиттанса (13)-(14) приобретают более сложный вид, требующий отдельного рассмотрения, выходящего за рамки настоящей работы.   

6. Волновое число и адмиттанс в присутствии проводимости

Согласно методу пошагового алгоритма, амплитуды волн в слоях определяются значениями волнового числа и адмиттанса. Рассмотрим, что происходит с этими параметрами при изменении проводимости, для чего обратимся к рис.4, где показаны зависимости диэлектрической проницаемости (а), волнового числа (б) и адмиттанса (в) от проводимости.

При построении рисунка частота была выбрана равной  из того соображения, что такой диапазон СВЧ является рабочим для широкого класса устройств на ферритах [8-10,19-21], на метаматериалах [22], а также используется в спин-волновой электронике [23].

На рисунке сплошными линиями показаны действительные части соответствующих величин, пунктирными – мнимые их части.  

Интервал рассмотренных значений проводимости выбран таким образом, чтобы действительные и мнимые части различались друг от друга заметным образом. Этим условием можно определить критическое значение проводимости:

.                                                                                                     (18)

При  неравенство (15) резко не выполняется, то есть среда ведет себя преимущественно, как диэлектрик.

При  неравенство (15) выполняется, то есть среда ведет себя, как металл.

Случай  соответствует полупроводящей среде.

Можно видеть, что это критическое значение соответствует критерию перехода между диэлектриком и металлом, введенному в работе [24, форм.(27)]:

,                                                                                               (19)

который переходит в (18) при .

   

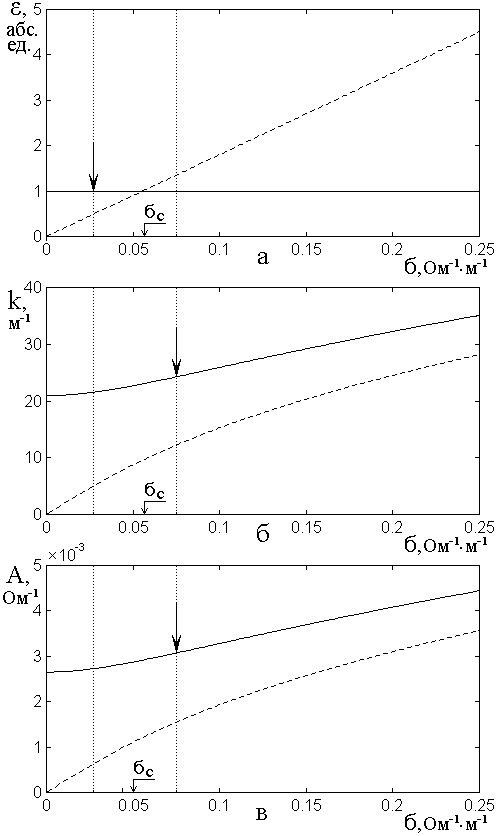
Рис.4. Зависимости диэлектрической проницаемости (а), волнового числа (б) и адмиттанса (в) от проводимости. Сплошные линии – действительные части соответствующих величин, пунктирные – мнимые их части.

Частота: . Параметры среды: , .

 

В рассматриваемом здесь случае, полагая , , , получаем: . Именно такая величина на рисунке лежит в левой части исследуемого диапазона.

Видно, что левее этого значения проводимости действительные величины диэлектрической проницаемости  (рис.4а) и особенно волнового числа  (рис.4б) и адмиттанса  (рис.4в) заметно превышают их мнимые части, то есть среду можно считать по преимуществу диэлектрической с некоторой проводимостью, то есть как бы «плохим полупроводником».

Правее этого значения мнимые части становятся заметными, после чего начинают преобладать над действительными, в результате чего действительная и мнимая ветви для волнового числа (рис.4б) и адмиттанса (рис.4в) сближаются («хороший полупроводник»). Далее (за правым краем рисунка) мнимая часть еще более сближается с действительной, причем зависимость от проводимости приобретает корневой характер в соответствии с выражениями (16)-(17) («металл»).

Для определенности на рисунке проведены вертикальные точечные линии через те значения проводимости, где действительные части  исследуемых параметров превышают мнимые в два раза. Для диэлектрической проницаемости (рис.4а) это соответствует проводимости  (левая точечная линия). Для волнового числа (рис.4б) и адмиттанса (рис.4в) – проводимости  (правая точечная линия, как следует из (10)-(11) и (13)-(14), для обоих параметров совпадает). Соответствующие значения действительных частей исследуемых параметров показаны стрелками.

Можно видеть, что критическая величина проводимости  находится вблизи от середины между этими значениями.

Хотя видно, что диэлектрическая проницаемость (рис.4а) более чувствительна к величине проводимости, чем волновое число (рис.4б) и адмиттанс (рис.4в), однако в ходе пошагового алгоритма фигурируют именно эти два последних параметра, то есть можно полагать, что проводимость должна существенно сказываться на распределении амплитуд волн в слоях начиная именно с приведенного критического значения.   

7. Характер проникновения волны в металл

Из (18) можно видеть, что при увеличении частоты критическое значение проводимости также увеличивается. То есть, казалось бы,  на более высоких частотах диэлектрические свойства среды относительно законов распространения волны проявляются до более высоких значений проводимости.

Однако, благодаря мнимой составляющей волнового числа (11), образующейся за счет проводимости, амплитуда волны по мере распространения в среде уменьшается. Так в соответствии в классическим критерием убывания амплитуды в  раз, то есть полагая , из (16) получаем «глубину проникновения» волны в металл, обусловленную скин-эффектом:

,                                                                                          (20)

совпадающую с классикой [15-17,25,26].

Таким образом, при увеличении частоты, хотя действительная часть адмиттанса относительно мнимой еще может оставаться достаточно высокой, но амплитуда волны в среде настолько резко затухает, что волна сохраняет способность проникать через слой тем меньшей толщины, чем проводимость больше. 

Интересно проверить соотношение частоты, соответствующей критической проводимости, с глубиной проникновения волны реальный металл. Так, разрешая (20) относительно частоты:

                                                                                                 (21)  

и подставляя типичное значение для металла значение проводимости  [24,27], получаем: . Такая частота соответствует длине волны , которая приближается к границе ультрафиолетового и рентгеновского диапазонов. При такой частоте, согласно (20) (при ), глубина проникновения равна:  . То есть в реальном металле на частоте, соответствующей критической проводимости, волна затухает по амплитуде почти в три раза на расстоянии меньшем четверти ее длины, так что распространение волны является полностью апериодическим.

8. Распределение амплитуд для электромагнитной волны

Теперь, после того как основные закономерности распространения волн в периодической структуре с диссипацией на примере одномерной волны рассмотрены, обратимся к более сложному случаю электромагнитной волны.

Здесь, в отличие от одномерной волны, определяющим параметром является не волновое число, а частота, задаваемая источником возбуждения. Геометрию задачи будем полагать той же самой (рис.1). В качестве возбуждения будем считать амплитуду электрического поля волны прямого направления в слое №1, то есть , на которую будем нормировать поля во всех остальных слоях. Источником диссипации волны полагаем электрическую проводимость материала каждого слоя.

В качестве инструмента расчета будем пользоваться пошаговым алгоритмом, вариант которого для электромагнитной волны описан в работе [2], причем для получения волнового числа и адмиттанса в среде с проводимостью используем выражения (10)-(11) и (12)-(13).

Основные результаты иллюстрируются рис.5, где показаны распределения нормированных амплитуд волн прямого (сплошные линии и сплошные точки) и обратного (пунктирные линии и открытые точки) направлений от координаты при различных значениях  проводимости.

 

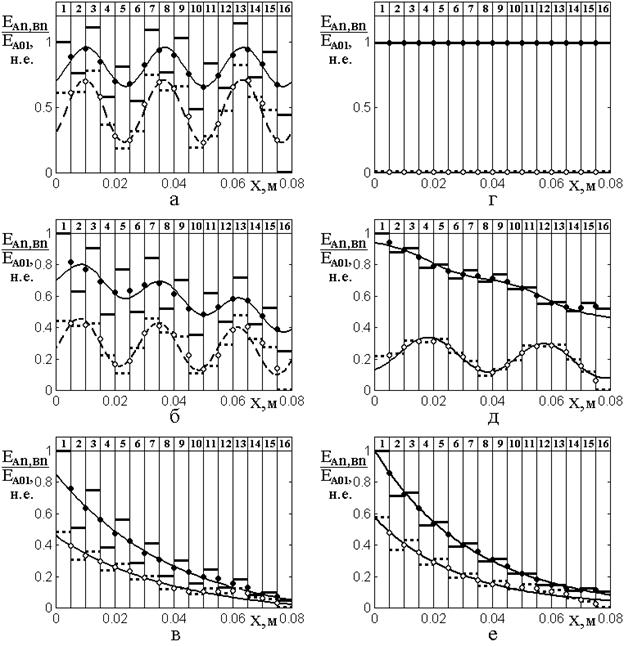
Рис.5. Распределение нормированных амплитуд волн прямого (сплошные линии и сплошные точки) и обратного (пунктирные линии и открытые точки) направлений от координаты при различных значениях  проводимости.

Критическое значение проводимости: . Частота – . Параметры: везде , в промежутке: , . Внутри барьера: а,б,в – , г,д,е –  . Проводимость барьера:

а – ;   б – ;   в –  ; г – ;   д – ;   е –  .

 

При построении рисунка значения диэлектрической проницаемости барьеров  были подобраны таким образом, чтобы в случаях а,б,в она значительно (в  раз) превышала таковую для промежутка , тогда как в случаях г,д,е обе проницаемости равнялись друг другу: .

При этом проводимости в случаях а,б,в и  г,д,е нарастали от нуля в случаях а,г до превышения над критической проводимостью  в  и  раза в случаях в и е соответственно.  

Различные значения превышения для левого ( раз) и правого ( раза) столбцов на рис.5 были выбраны для обеспечения большей наглядности рисунка, исходя из максимально возможного соответствия характера распределений случаю одномерной волны. В то же время, для близкого характера изменений распределения амплитуд между столбцами в случае правого столбца требовалось меньшее значение проводимости, чем для левого из-за того, что в левом столбце проводимость барьера действовала на фоне довольно высокой диэлектрической проницаемости, тогда как в правом – на нулевом фоне по сравнению с промежутком.  

Для построения непрерывных кривых на рис.5 использовались следующие эмпирические формулы (с точностью до постоянной составляющей и сдвига фазы): 

а – ;

      ;                                            (22)

б – ;

                                     (23)

в – ;

     ;                                          (24)

г – ; 

     ;                                                                 (25)

д – ;   

     ;                                   (26)

е – ;

     .                                           (27)

Распределение, приведенное на рис.5а, соответствует отсутствию проводимости барьера и показано здесь для сравнения.

Распределения, приведенные на рис.5б,д  и 5в,е, соответствуют относительно малой (б,д) и сравнительно большой (в,е) проводимостям барьера. 

Распределение, приведенное на рис.5г, соответствует точному равенству диэлектрической и магнитной проницаемостей барьера и промежутка при нулевой проводимости обоих. То есть неоднородность структуры в целом отсутствует и волна, не испытывая отражения, полностью проходит насквозь.

Распределения, приведенные на рис.5б и 5в соответствуют малой (б) и большой (в) проводимостям барьера на фоне относительно большой диэлектрической проницаемости барьера в сравнении с таковой для промежутка. 

Распределения, приведенные на рис.5д и 5е соответствуют малой (д) и большой (е) проводимостям барьера на фоне равенства диэлектрических проницаемостей барьера и промежутка. 

Из рис.2 можно видеть, что в рассматриваемом случае отличной от нуля проводимости наблюдаются те же основные виды распределений, что и при ее отсутствии [1,2], а также для случая одномерной волны, рассмотренном здесь в разделе №2. 

Более точно наблюдаемые распределения можно классифицировать следующим образом:

а – синусоидальное;

б – линейное с добавкой синусоидального, называемое далее линейно-синусоидальным;

в – экспоненциальное;

г – постоянное;

д – для волн прямого направления – практически линейное с незначительной (около  от максимума) добавкой синусоидального, для волн обратного направления – синусоидальное с большой амплитудой и незначительной (около тех же ) добавкой линейного; 

е – экспоненциальное для волн обоих направлений.

Отметим некоторые особенности, следующие из общего вида приведенных кривых.

На рис.5а обе синусоиды имеют одинаковый период и одинаковую фазу; средний уровень амплитуды волн прямого направления () выше среднего уровня амплитуды волн обратного направления () почти в два раза.

На рис.5б коэффициент линейного спада для волн прямого направления () больше коэффициента линейного спада волн обратного направления () примерно в четыре раза. Соотношение средних уровней синусоидальных составляющих амплитуд волн прямого () и обратного () направлений – обратное по сравнению с таковым на рис.5а и составляет около двух раз. 

Для волн прямого направления  средний уровень вблизи  составляет , амплитуда синусоидальной составляющей – , отношение этих величин – около  раз. Для волн обратного направления  средний уровень вблизи  составляет , амплитуда синусоидальной составляющей – , отношение этих величин близко к .

Таким образом, для волн прямого направления в распределении преобладает линейная составляющая, для волн обратного направления – преобладает синусоидальная составляющая, хотя здесь такое преобладание выражено значительно слабее, чем для одномерной волны: там в  раз, здесь – всего в  раза.

Такое различие, по-видимому, вызвано большим различием диэлектрических проницаемостей барьера и промежутка здесь, чем в случае одномерной волны для волновых чисел. Так в пересчете на волновое число здесь различие составляет  раз, тогда как для одномерной волны: . Хотя, по такому пересчету отношение здесь составляет всего , что мало отличается от единицы, можно полагать, что электромагнитная волна более чувствительна к изменению проводимости, чем одномерная к изменению волнового числа.

Возможной причиной такой более высокой чувствительности может быть то обстоятельство, что в формировании волнового возмущения в электромагнитной волне участвуют два поля – электрическое и магнитное, тогда как в одномерной волне всего одно – смещение по координате, то есть электромагнитная волна по эффективности связана со средой распространения как бы сильнее, чем одномерная.

На рис.5в обе зависимости описываются одной и той же экспонентой, различие состоит только в линейном числовом коэффициенте: для волн обратного направления он составляет  от такого же коэффициента для волн прямого направления. Как видим, здесь этот коэффициент превышает таковой для одномерной волны () более чем в три раза, что может быть вызвано той же причиной.

Подобные особенности наблюдаются и для кривых, приведенных на рис.5г,д,е.

Характерна наблюдаемая при сравнении горизонтальных пар рисунков несколько более слабая зависимость распределений от координаты, свойственная первым двум эпюрам правого столбца (рис.5г,д) по сравнения с таковыми для левого (рис.5а,б).

Однако здесь, в отличие от случая одномерной волны, такая «слабость» выражена значительно меньше. Так здесь отношение средних уровней для волн прямого и обратного направлений на рис.5б составляет , а на рис.5д – , то есть увеличивается примерно в три раза. Для одномерных же волн, как можно видеть из рис.2б, 2д, подобные же цифры равны  и , то есть отношение увеличивается всего в полтора раза.

То есть здесь наблюдается то же увеличение «чувствительности» электромагнитных волн к диссипации по сравнению с одномерными, обусловленное той же причиной.    

На рис.5в и 5е экспоненты в обоих случаях почти не отличаются, что говорит о преобладании роли проводимости над диэлектрической проницаемостью при экспоненциальном распределении.

Здесь опять проявляется сильно выраженное повышение «чувствительности» электромагнитной волны к диссипации над одномерной волной. Так отношение начальных амплитуд на рис.2в и 2е равно  и  соответственно, что дает соотношение в  раз, тогда как для электромагнитной волны, как видно из рис.5в и 5е эти же цифры составляют  и , а их отношение – всего  раз, то есть более чем вдвое меньше. 

Таким образом, несмотря на то, что в формировании распределений в левом столбце рис.5 участвует наряду с проводимостью также и диэлектрическая проницаемость, тогда как в формировании распределений правого столбца только проводимость, влияние проводимости для электромагнитной волны значительно преобладает над влиянием диэлектрической проницаемости, в отличие от случая одномерной волны, где такое соотношение является обратным.

9. Сочетание различных видов распределений

Отметим еще одну характерно выраженную особенность приведенных зависимостей, явно параллельную подобной особенности для одномерной волны.

Так отличие от случая отсутствия проводимости здесь состоит в том, что синусоидальное распределение не является самостоятельным, а накладывается на линейное (особенно хорошо это заметно на рис.5в, а также частично на рис.5д), образуя распределение линейно-синусоидальное.

Наблюдаемое здесь линейное распределение не является переходным от синусоидального к экспоненциальному, а получается как результат убывания амплитуд волн того и другого направлений при удалении их от точки возбуждения (то есть от слоя №1). Очевидно, такое убывание является следствием затухания волны по координате, что описывается мнимой составляющей диэлектрической проницаемости, обеспечиваемой проводимостью (7).

Когда мнимая составляющая диэлектрической проницаемости (7) становится достаточно большой, линейно-синусоидальное распределение сменяется экспоненциальным, как это видно из рис.5в и 5е. Однако здесь спадающий характер распределения обусловлен не наличием «полос непропускания» в отсутствие проводимости, определяемых интерференцией волн при их многократном переотражении [2], а именно затуханием волны по мере ее распространения по координате. Это хорошо видно из сравнения рис.5а с рис.5в, где действительная диэлектрическая проницаемость соответствует области пропускания, тогда как распределение на рис.5в спадает по экспоненте. То же следует из сравнения рис.5г с рис.5д и 5е, где действительная часть диэлектрической проницаемости в переотражении волн вообще не участвует, так как ее значения для барьеров и промежутков между собой равны. Тем не менее, обеспечиваемая проводимостью достаточно большая мнимая составляющая проницаемости и здесь приводит к спаду распределения сначала по линейному закону (рис.5д), а затем по экспоненте (рис.5е).

Таким образом, из проведенного рассмотрения видно, что проводимость, обеспечивая мнимую добавку к действительной диэлектрической проницаемости, может приводить к таким же видам распределения амплитуд в слоях, что и действительная диэлектрическая проницаемость, однако главная ее роль состоит в уменьшении амплитуд волн по координате по мере удаления от источника возбуждения, которое накладывается на распределения, обусловленные действительной диэлектрической проницаемостью. 

При этом влияние проводимости на диссипативные свойства электромагнитной волны сказывается значительно (более чем в два-три раза) сильнее, чем влияние мнимой части волнового числа на те же свойства для одномерной волны, причиной чего может явиться участие в формировании распределений амплитуд одновременно обоих полей волны – электрического и магнитного, что приводит к повышению эффективности связи волны со средой распространения. 

10. Сравнение эффективности диссипации

В предыдущем разделе был сделан вывод о том, что влияние проводимости на диссипацию электромагнитной волны сказывается значительно (более чем в два-три раза) сильнее, чем влияние мнимой части волнового числа на то же свойство для одномерной волны. Однако параметры, использованные при построении распределений на рис.5, будучи выбранными из условия сходства характера распределений случаю одномерной волны, не были эквивалентны подобным параметрам, принятым при построении рис.2. Такое обстоятельство не позволило сравнить диссипативные свойства этих случаев в достаточной полноте.   

Для сравнения эффективности механизмов диссипации для одномерной и электромагнитной волны зададим диэлектрическую проницаемость и проводимость таким образом, чтобы волновые числа барьера и промежутка были пропорциональны таковым для одномерной волны.

Так для одномерной волны при построении рис.2в были приняты следующие параметры:

волновое число промежутка: ,

волновое число барьера:  . 

При построении рис.2е те же параметры равнялись:

волновое число промежутка: ,

волновое число барьера:  . 

Потребуем выполнения условий пропорциональности действительных и мнимых частей волновых чисел:  

;                                                                           (28)

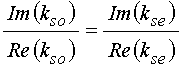,                                                                            (29)

где индексами «» и «» отмечены волновые числа для одномерной и электромагнитной волны соответственно.

Из условий (28)-(29) находим:

;                                                             (30)

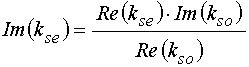.                                                              (31)

Для электромагнитной волны в промежутке воспользуемся определением волнового числа:

 ,                                                                                 (32)

из которого при частоте  и , , получаем:

.                                                      (33)

Согласно (30)-(31), получаем волновое число для электромагнитной волны внутри барьера при отличной от единицы диэлектрической проницаемости: 

.                                                   (34)

При этом, в соответствии с (32), действительная часть диэлектрической проницаемости равна: . В случае  вместо (34) получаем:

.                                                  (35)

Для нахождения значения проводимости, требуемой для обеспечения мнимой части волнового числа для электромагнитной волны внутри барьера , разрешим (11) относительно проводимости:

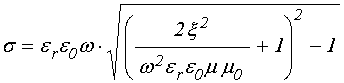.                                           (36)

Подставляя в эту формулу , получаем: . При  соответственно получаем: .

Рассмотрим теперь рис.6, где показаны распределения нормированных амплитуд волн прямого (сплошные линии и сплошные точки) и обратного (пунктирные линии и открытые точки) направлений от координаты при различных значениях  проводимости.

 

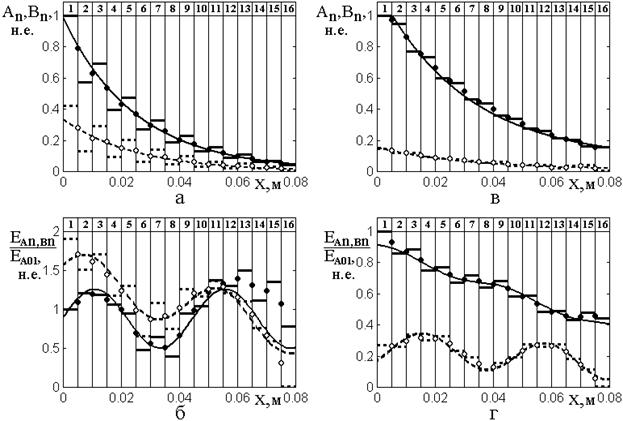
Рис.6. Распределение нормированных амплитуд волн прямого (сплошные линии и сплошные точки) и обратного (пунктирные линии и открытые точки) направлений от координаты при различных значениях  проводимости.

а,в – одномерная волна, параметры – те же, что на рис.2в, 2е.

б,г – электромагнитная волна. Частота – .

Параметры: везде , в промежутке: , .

б –  , ;

г –  , .

 

Волновые числа, соответствующие распределениям, приведенным на рис.6:

а – ,  ;

б – , ;

в – ,  ;

г – , .

Верхний ряд эпюр (а,в) соответствует одномерной волне, нижний (б,г) – электромагнитной. Параметры структуры, в которой распространяется электромагнитная волна, подобраны таким образом, чтобы волновые числа в промежутках и барьерах были пропорциональны волновым числам для одномерной волны (то есть – в соответствии со значениями, приведенными выше).

Из сопоставления верхнего и нижнего рядов рисунков видно, что при одинаковом соотношении действительных и мнимых частей волнового числа для одномерной волны (а,в) распределения становятся экспоненциальными, тогда как для электромагнитной волны (б,г) сохраняется преобладающая синусоидальная составляющая. При этом, когда действительная компонента волнового числа барьера отличается от таковой для промежутка (а,б), такое преобладание выражено сильнее, чем в случае, когда эти компоненты равны (в,г).

То есть при установлении эквивалентности параметров структур по волновым числам, влияние проводимости на затухание волны проявляется слабее, чем такое же влияние за счет мнимой составляющей волнового числа. 

Этот вывод находится в определенном противоречии со сделанным в предыдущем разделе. Однако надо учесть, что здесь для установления пропорциональности между волновыми числами проводимость для рис.6б положена равной , тогда как для рис.6г – ее пришлось уменьшать до величины , то есть более чем в два раза (точнее – в  раза). Такое уменьшение проводимости соответственно уменьшило ее влияние на затухание волны, что и привело к сохранению синусоидальной составляющей на рис.6б и 6г.

То есть, можно полагать, что сделанный в предыдущем разделе вывод о более высокой эффективности взаимодействия электромагнитной волны со средой по сравнению с таковой для одномерной волны обусловлен принятием там более высокого значения проводимости, что было сделано, исходя из требования сходного характера распределений в правом и левом столбцах рис.2.

Замечание. Сделанный здесь вывод является по сути дела качественным, имеющим силу при принятых параметрах задачи. Для более корректного ответа на вопрос об эффективности взаимодействия волны со средой, по-видимому, должен быть введен какой-то параметр взаимодействия, величина которого была бы критерием такой эффективности. В основу определения такого параметра можно положить или волновое число, как это сделано здесь, или сходство характеров распределений при заданном различии диэлектрических проницаемостей барьеров и промежутков, как это сделано в предыдущем разделе. По-видимому, возможны и другие варианты, однако на данном этапе задача получения такого параметра выходит за рамки настоящей работы. 

11. Отражающие и пропускающие свойства структуры для электромагнитной волны

Рассмотрим теперь, какое влияние оказывает проводимость на отражающие и пропускающие свойства структуры относительно электромагнитной волны.

Предварительное исследование показало, что частотная зависимость отражающих и пропускающих свойств структуры относительно электромагнитной волны во многом подобна зависимости от волнового числа для одномерной волны, рассмотренной в разделе №4. То есть и здесь спектр имеет дискретную структуру, образованную чередованием областей пропускания и непропускания. При увеличении затухания области пропускания-непропускания остаются на своих местах, задаваемых действительной частью волнового числа, то есть их чередующийся характер от величины затухания не зависит. 

Однако в отличие от случая одномерной волны здесь затухание волн обоих направлений, обусловленное проводимостью, не приводит к сильному уменьшению амплитуды волн при увеличении частоты. То есть, в более высокочастотных областях пропускания и непропускания амплитуда распространяющихся волн сохраняется на такой же величине, какой она была в низкочастотных. В ходе настоящей      работы такое свойство было проверено вплоть до пятой-седьмой областей непропускания, то есть при принятых параметрах (, , , , ) на частотах до .

С другой стороны, дискретный характер структуры каждой области, заметнее проявляющийся при , при повышении частоты от  до  несколько сглаживается: амплитуда изрезанности областей падает в полтора-два раза, что аналогично подобному свойству для одномерной волны.

В то же время, для электромагнитной волны наблюдается ряд особенностей, заметно отличающих ее свойства от таковых для одномерной волны, на более подробном рассмотрении которых здесь и остановимся.

Обратимся к рис.7, где на примере одной области показаны зависимости нормированных амплитуд волн обратного в слое №1 (а,б,в) и прямого в слое №16 (г,д,е) направлений от частоты возбуждения при различных значениях проводимости.

   

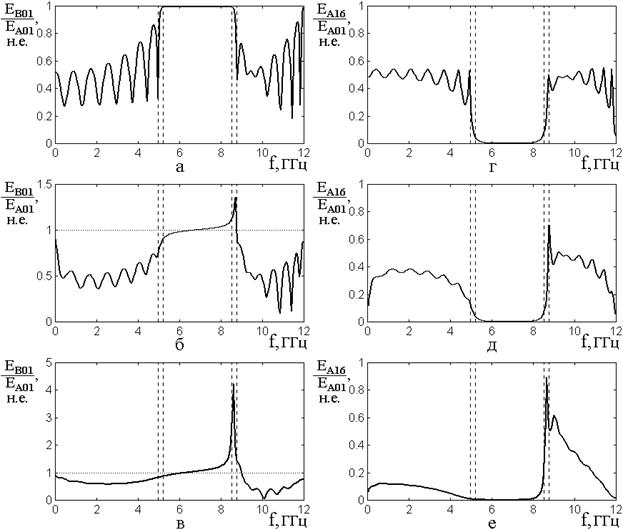
Рис.7. Зависимости нормированных амплитуд волн обратного в слое №1 (а,б,в) и прямого в слое №16 (г,д,е) направлений от частоты возбуждения при различных значениях проводимости относительно критического значения .

а,в – ;      б,д – ;      в,е – .

Параметры: , , , .

 

Приведенный частотный интервал соответствует первой области непропускания, края которой отмечены парными вертикальными пунктирными линиями. Эти края по уровню отражения  соответствуют частотам  и , а середина приходится на частоту . В работе [2, форм.(66)] для расчета центральной частоты первой области непропускания получена формула: 

.                                             (37)

Подставляя приведенные здесь значения, получаем частоту , что несколько ниже наблюдаемой величины. Подобное занижение в ряде случаев отмечалось в той же работе [2], для компенсации чего были введены поправочные коэффициенты, для случаев слабой и сильной неоднородности равные  и . С помощью этих коэффициентов получаем частоты  и , первая из которых ниже наблюдаемой, а вторая – выше. Для рассматриваемого здесь случая наиболее подходит коэффициент , занимающий как раз промежуточное значение между приведенными в работе [2]. Таким образом, с учетом этого коэффициента можно считать согласие приведенной формулы с полученным расчетным значением вполне удовлетворительным.  

    В той же работе [2] показано, что первая область непропускания по резонансным свойствам подобна электродинамическому резонатору длиной  с диэлектрической проницаемостью равной средней величине между проницаемостями барьера и промежутка, то есть .

    При построении приведенных на рис.7 зависимостей использовались значения , , то есть усредненное значение равно . Подставляя это значение и частоту середины области непропускания  в формулу (18), получаем критическое значение проводимости .

    Как можно видеть из рис.4, при таком критическом значении действительные части волнового числа и адмиттанса превышают мнимые несколько более чем в два раза (точнее – в  раза). То есть можно ожидать, что при  решающую роль в формировании области непропускания играют еще действительные части волнового числа и адмиттанса, а начиная с  роль мнимых частей становится значительной.

В соответствии с этим при построении зависимостей на рис.7 были приняты следующие значения проводимости: для рис.7б,д  – , что значительно меньше , а для рис.7в,е –  , что как раз равно . Зависимости на рис.7а,г соответствуют отсутствию проводимости и приведены здесь для сравнения.

Из рис.7а,г видно, что в отсутствие проводимости внутри области непропускания амплитуда от частоты не зависит, тогда как по обе стороны от краев области амплитуда имеет осциллирующий характер. Подобная структура области, представляющая собой большой центральный лепесток, сопровождаемый по сторонам лепестками-сателлитами спадающей амплитуды, отмечалась в работах [1] для одномерной волны и [2] для электромагнитной волны, то есть, как и там, обусловлена интерференционными явлениями при многократном переотражении волн обоих направлений.

При увеличении проводимости до уровня   (рис.7б,д) дискретный характер сателлитов сглаживается, амплитуда их размаха падает в  раз и более, что обусловлено частичным затуханием интерферирующих волн за счет проводимости.

При увеличении проводимости до , то есть до критического значения (рис.7в,е), сателлиты совсем пропадают, а на их месте появляются плавные участки отражения (рис.7в) или прохождения (рис.7е). Уровни отражения при этом примерно соответствуют среднему уровню в отсутствие проводимости (около ), тогда как для прохождения, особенно ниже основного лепестка, снижаются в несколько раз (с  до ). Такое сохранение уровня для отраженной волны в сочетании с его падением для волны проходящей, по-видимому, обусловлено тем, что в отражении волны в слой №1, откуда происходит возбуждение, решающую роль играют слои, наиболее близкие к этому первому слою, где волна еще не успевает затухнуть в значительной степени. Падение уровня проходящей волны в слое №16 происходит из-за того, что волна до попадания в этот слой должна пройти через множество промежуточных слоев, в каждом из которых она частично затухает. То есть в формировании волны в последнем слое участвуют все промежуточные слои структуры, каждый из которых, внося свой вклад в общее затухание, приводит к совокупному значительному уменьшению амплитуды проходящей волны.  

12. Диссипативный резонанс

Важной особенностью наблюдаемых на рис.7 амплитудно-частотных характеристик отражения и прохождения является наличие резкого выброса амплитуды вверх на высокочастотном конце области (между двумя правыми по рисунку пунктирными линиями). Максимум наблюдаемого пика соответствует частоте , а края на половине высоты приходятся на частоты  и , то есть ширина составляет . По уровню  от максимума края приходятся на частоты  и  откуда получаем ширину , что соответствует добротности резонансной системы .

С другой стороны, амплитуда пика при увеличении проводимости также увеличивается. Так для отражения при проводимости  (рис.7б) его максимум составляет , а при проводимости  (рис.7в) уже достигает  Такой же рост амплитуды пика наблюдается и для прохождения (с  на рис.7д при  до  на рис.7е при ).

Таким образом, наблюдаемый пик во-первых связан с геометрическими размерами структуры, о чем говорит его расположение точно на высокочастотном краю области непропускания, и во вторых – обусловлен именно проводимостью определенных слоев, о чем говорит его рост при увеличении проводимости. То есть по характеру частотной зависимости и обусловленности проводимостью его можно назвать «диссипативным резонансом».

13. Аномалия баланса потоков энергии

Другой важной особенностью приведенных амплитудно-частотных зависимостей является наблюдаемое на рис.7б и 7в  превышение амплитуды отраженной волны над амплитудой возбуждающей. Такое превышение наблюдается при проводимости  (рис.7б) в интервале частот от  до , а при проводимости  (рис.7в) происходит в еще более широком диапазоне частот  от  до , захватывая также диссипативный резонанс.

С физической стороны превышение амплитуды отраженной волны над амплитудой падающей означает увеличение потока энергии отраженной волны по сравнению с потоком энергии падающей, что находится в определенном противоречии с законом сохранения энергии.

Такое обстоятельство в диссипативных средах, в том числе обладающих проводимостью, вообще говоря, более или менее известно. Так в классической монографии [28] не только обозначается такая проблема, но и упоминается многолетняя дискуссия на эту тему. Неоднократно отмечено, что превышение суммарного потока энергии волн, выходящих из структуры – отраженной и проходящей над потоком энергии падающей волны имеет место при прохождении волны из диссипативной среды в бездиссипативную [29-34].

Для преодоления такого противоречия предложен ряд приемов, в том числе введение «фиктивного» слоя [32], учет неоднородности электромагнитных волн вблизи границы раздела сред [31], привлечение для выполнения баланса энергии понятия интерференционного потока [33,34], введение нового специального вида определения энергетического коэффициента прохождения волны [30], опять же на основе интерференционного потока.

В работе [35] для выполнения баланса энергии в случае одномерной волны для структуры из трех диссипативных сред, разделенных двумя границами, предложено использовать кроме потоков энергии отраженного и проходящего, также поток локализованный, содержащий активную и реактивную части. Такая модель обеспечивает выполнение баланса энергии в случае представления распространяющихся волн в комплексном виде. Некоторое расширение этой модели в том числе для электромагнитных волн и магнитных сред, выполнено в работах [36-41]. Однако общая задача о балансах энергии волн, распространяющихся в многослойной структуре, требует более подробного рассмотрения, выходящего за рамки настоящей работы. Можно полагать, что, как и в работах [35-41], к определенному успеху приведет использование  комплексных потоков энергии с учетом локализации активной и реактивной составляющих в промежуточных слоях такой структуры.

Замечание.  Появление дополнительного резонанса, обусловленного диссипативными свойствами структуры, вообще говоря, является несколько неожиданным. Для проверки возможности существования такого резонанса было выполнено контрольное исследование распространения электромагнитной волны в многослойной структуре, все слои которой обладают одинаковой диэлектрической и магнитной проницаемостями, но чередующейся от слоя к слою проводимостью. Было получено, что диссипативный резонанс имеет место и в этом случае, причем его амплитуда с увеличением проводимости увеличивается, но не монотонно, а переменным образом, при некоторых значениях проводимости достигая весьма больших величин, а при других падая до малых. Так при равенстве проводимости критическому значению  амплитуда диссипативного резонанса достигала  по проходящей волне и  по отраженной, при проводимости  амплитуды возрастали до  и   соответственно, а при  снова падали до  и  При этом частота диссипативного резонанса при  составляла , а при  линия раздваивалась на две при частотах  и . Вообще говоря, по-видимому, природа диссипативного резонанса – та же, что и природа превышения потоков энергии выходящих волн над входящими. В пользу этого говорит единый непрерывный характер частотных зависимостей, при которых диссипативный резонанс является как бы продолжением частотной характеристики внутри области непропускания. Однако вопрос в целом представляется довольно сложным и требует отдельного рассмотрения.

14. Особенности случая металлической проводимости

Проведенное в предыдущих разделах рассмотрение для электромагнитной волны выполнено в условиях, сходных с таковыми для одномерной волны. То есть проводимость выбиралась такой, чтобы порядок величин действительной и мнимой частей волнового числа был близким. Это было сделано для того, чтобы, во-первых, рассмотреть возможные варианты соотношений величин действительной и мнимой частей, и во-вторых, результаты, получаемые для электромагнитной волны удобно было бы сравнивать с таковыми для одномерной волны. При этом проводимость составляла не более нескольких единиц , что соответствует полупроводниковым материалам [24,27]. Однако при этом оставался за пределами рассмотрения широкий класс материалов с более высокой проводимостью, каковой обладают металлы. Так для металлов типичное значение проводимости составляет порядка  и даже несколько более [24,27,42,43]. То же касается проводимости некоторых композиционных сред, в том числе содержащих металлические гранулы в диэлектрической матрице [44-48]. Поэтому в рамках данной работы представляет интерес рассмотрение периодических структур, барьеры которых обладают именно металлической проводимостью, что и сделано далее.

15. Распределение амплитуд при металлической проводимости

В случае металлической проводимости, как это видно из разделов №5-6, мнимая часть комплексной диэлектрической проницаемости (7) значительно (на несколько порядков) превышает действительную, а мнимые части волнового числа (11) и адмиттанса (14) приближаются к действительным частям тех же величин. При этом на рассматривавшихся выше частотах СВЧ диапазона () глубина проникновения поля волны в металл (20) становится на несколько порядков меньше принятой в том рассмотрении не только полной длины структуры (), но и  толщины одиночного барьера (). В такой ситуации является очевидным тот факт, что волна не только не проходит через структуру, но и отражается практически целиком на толщине одного  барьера, то есть распределение амплитуд волн с слоях структуры становится экспоненциальным с весьма высоким показателем. Поэтому для выявления разнообразия распределений имеет смысл рассмотрение таких структур, где толщина барьера имеет тот же порядок, или менее, чем глубина проникновения, то есть в рассматриваемом диапазоне частот и проводимостей  составляет единицы микрометров.

Для такого рассмотрения обратимся к рис.8, где показаны распределения нормированных амплитуд волн прямого и обратного направлений от координаты в случае металлической проводимости при различных значениях  толщины барьера. Частота выбрана равной . При проводимости барьера  и остальных типичных параметрах (, , ) глубина проникновения, согласно (20), составляет  . Исходя из условия не очень большого затухания волны на толщине барьера (не более чем в  раз), толщины барьеров выбраны в интервале от  (рис.8а) до  (рис.8г). При этом, учитывая, равенство толщин барьера и промежутка (), полная длина структуры , содержащей  слоев (рис.1), получается равной от (рис.8а) до  (рис.8г), с промежуточными значениями  (рис.8б) и (рис.8в) при толщинах барьеров  и  соответственно.

Для показанных на рис.8 распределений построение непрерывных кривых осуществлялось с помощью следующих эмпирических формул (с точностью до постоянной составляющей и сдвига фазы): 

а – ;                                                                  (38)

б – ;                                                    (39)

в – ;                    (40)

г –                                       (41)

В ходе построения рис.8 было выявлено, что при принятых параметрах частоты и проводимости амплитуды волн прямого и обратного направлений в каждом отдельном слое совпадают друг с другом с точностью  Поэтому в приведении отдельных данных для каждого из направлений в принятом масштабе рисунка не было необходимости. Таким образом, показанные на рис.8 уровни амплитуд относятся к волнам как прямого, так и обратного направлений в равной степени.

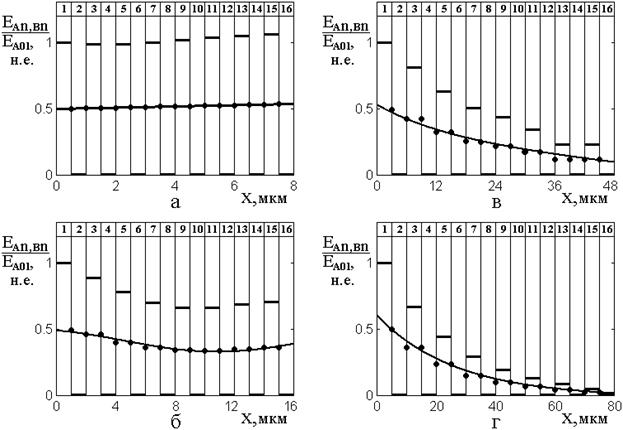
Рис.8. Распределение нормированных амплитуд волн прямого и обратного направлений (совпадают) от координаты в случае металлической проводимости при различных значениях  толщины барьера. Частота – .

Толщина барьеров: а – ; б – ; в – ; г – .

Параметры: , , ,  .

 

Из рис.8 видно, что при металлической проводимости в выбранном диапазоне толщин совокупность наблюдаемых распределений, в общем подобна таковой для случая полупроводящей среды (раздел №8). 

Так распределение на рис.8а, соответствующее структуре, для которой глубина проникновения превышает толщину барьера на порядок, согласно принятой в разделе №2 терминологии, является постоянным.

Распределение на рис.8б, где глубина проникновения превышает толщину барьера в пять раз, является синусоидальным, однако, благодаря тому, что период его составляет , то есть более чем вдвое превышает длину структуры (), его можно считать уже полусинусоидальным [1], то есть переходным от синусоидального к линейному. 

Распределение на рис.8в, где глубина проникновения превышает толщину барьера всего в  раз, представляет собой сумму экспоненциального и линейного, хотя линейный его характер еще выражен более явно, чем экспоненциальный. Так отклонение от прямой, проведенной через точки 7-16 слоев для слоя №1, где оно максимально, не превышает . Следы же синусоиды в этом случае уже отсутствуют.

Распределение на рис.8г, где глубина проникновения равняется толщине барьера (с точностью более ),  является ярко выраженным экспоненциальным, без заметного вклада линейного и тем более синусоидального.

Таким образом, можно сделать вывод, что в формировании распределений, отличных от чисто экспоненциального (рис.8а-в), необходимым условием является превышение глубины проникновения над толщиной барьера в полтора-два и более раз. Заметим, что это относится именно к толщине барьера, но не к структуре в целом, длина которой может более чем на порядок превышать глубину проникновения (в рассматриваемых примерах – до  раз). 

Укажем дополнительно, что во всех рассмотренных случаях достаточно большая (сравнимая с единицей) амплитуда волн имеет место только внутри промежутков (нечетные слои), тогда как внутри барьеров величины полей значительно меньше и составляют порядка  Так для рис.8а, где распределение постоянно, амплитуды волн во всех промежутках близки к единице, тогда как амплитуда в слое №1 (первый барьер) составляет , а в слое №16 (последний барьер) равняется  На рис.8г, где распределение является ярко выраженным экспоненциальным, то есть по длине структуры значительно спадает, те же величины равны  и  соответственно.

То есть видно, что все перечисленные виды распределений проявляются достаточным образом уже на амплитудах, соответствующих только промежуткам (верхние участки утолщенных горизонтальных линий). 

16. Отражающие и пропускающие свойства структуры при металлической проводимости

Рассмотрим теперь, как сказывается металлическая проводимость на частотных свойствах структуры, для чего обратимся к рис.9, где показаны зависимости нормированных амплитуд волн обратного в слое №1 (а) и прямого в слое №16 (б) направлений от частоты возбуждения при различных значениях толщины барьера.

Для удобства сравнения с данными предыдущего раздела, значения  толщин барьеров выбраны теми же самыми. На рис.8, при построении которого частота выбрана равной , нормированная амплитуда в слое №1 при всех толщинах близка к единице, а нормированная амплитуда  при тех же условиях в слое №16 близка к нулю. Из рис.9 видно, что на той же частоте  в тех же слоях №1 и №16 эти величины составляют  и  , то есть отличаются от единицы и нуля на величины порядка , то есть  соответствие можно считать весьма хорошим.

 

Рис.9. Зависимости нормированных амплитуд волн обратного в слое №1 (а) и прямого в слое №16 (б) направлений от частоты возбуждения в случае металлической проводимости при различных значениях толщины барьера.

Толщина барьеров: а – ; б – ; в – ; г – .

Параметры: , , ,  .

 

Другой важной особенностью наблюдаемых частотных зависимостей является их плавный монотонный вид с полным отсутствием областей непропускания, имеющих место при малой проводимости (рис.7 здесь, а также рис.6 в работе [2]). Можно полагать, что такое отсутствие упомянутых областей, а также вообще какой-либо изрезанности обсуждаемых кривых, обусловлено общей тенденцией сглаживания амплитудно-частотных зависимостей при увеличении проводимости. Такое сглаживание было отмечено в разделе №11 уже при сравнительно малых ее значениях (рис.7в и 7е, где ), а здесь при металлической проводимости () оно проявляется с особой силой.

Из рис.9а далее видно, что до  амплитуда волн обратного направления в слое №1, то есть отраженных от структуры, при любой толщине с повышением частоты падает. Та же тенденция сохраняется при толщинах выше  (кривые 2,3,4) во всем диапазоне исследованных частот (до ). Такое уменьшение отражения обусловлено тем, что совокупная амплитуда обратно направленной волны в слое №1 складывается из амплитуд волн, отраженных от двух поверхностей каждого слоя. При этом, если волна внутри какого-либо слоя доходит до его противоположной поверхности без сильного ослабления, то после отражения от этой поверхности она складывается с той частью волны, которая отражается от первой поверхности до вхождения в слой. То есть суммарная амплитуда отраженной волны увеличивается. Если же волна на толщине слоя заметным образом затухает, то она уже не может внести вклада в общее отражение и суммарная амплитуда отраженной волны формируется только за счет отражения от передней поверхности слоя. Величина затухания волны в слое определяется глубиной проникновения волны в металл. Так если толщина слоя меньше глубины проникновения, то волна затухает мало и отражение получается большим. Если же толщина слоя больше глубины проникновения, то волна в слое затухает и отражение получается малым.

Как показано в предыдущем разделе, глубина проникновения на частоте  составляет около . На частоте  она уменьшается уже до . Соответственно на фиксированной частоте отражение должно быть тем больше, чем толщина барьера меньше. Это и наблюдается для всех исследованных структур на частотах от  до . Ниже  эта тенденция несколько нарушается, по-видимому, благодаря вступлению в игру интерференционных эффектов, проявляющихся на полной толщине структуры.

С другой стороны, по мере увеличения частоты волна все меньше проникает в слой, то есть затухает сильнее, в результате чего отражение уменьшается. Именно так на рис.9а ведут себя кривые 2 (толщина барьера – ), 3 () и 4 (). Подобным образом ведет себя и кривая 1, соответствующая толщине барьера , но только до частоты порядка .  Выше этой частоты кривая 1 идет вверх, стремясь к единице и, как следует из дополнительного исследования, несколько превышая ее (за правым краем рисунка), что может быть обусловлено явлениями разбаланса потоков энергии [28-41], упомянутыми в разделе №13. 

Обратимся теперь к рис.9б, где показаны подобные частотные зависимости для волн прямого направления в слое №16, соответствующие прохождению волны через структуру в целом. В соответствии со сказанным относительно соотношения толщины барьера с глубиной проникновения, естественно ожидать, что на любой заданной частоте по мере увеличения толщины барьера прохождение должно уменьшаться. Это и наблюдается на рис.9а: ниже всех идет кривая 4, которой соответствует наибольшая толщина, а выше – кривая 1 с толщиной наименьшей.

С другой стороны, по мере увеличения частоты при неизменной толщине, затухание волны должно увеличиваться, так как глубина проникновения волны при этом уменьшается, то есть волна на толщине барьера затухает сильнее. Это и наблюдается для толщин  и  (кривые 3 и 4 соответственно) на частотах выше , где интерференционные явления уже не сказываются. Для толщины  (кривая 2), начиная с частоты , наступает противодействующая тенденция, так что уменьшение прохождения сменяется почти горизонтальным участком, а для толщины  (кривая 1) эта тенденция становится преобладающей, приводя к росту прохождения по мере повышения частоты с последующим стремлением к насыщению на уровне порядка В качестве возможной причины можно предполагать и здесь проявление разбаланса потоков [28-41], аналогичное ответственному за рост кривой 1 на рис.9а.  

Таким образом, можно сделать вывод, что нормальное поведение частотных зависимостей, то есть по мере увеличения частоты уменьшение как отражения, так и  прохождения, имеет место только при толщинах барьеров, превышающих примерно четвертую-пятую часть от глубины проникновения. При меньших же толщинах по мере увеличения частоты как отражение, так и прохождение увеличиваются, что может быть обусловлено энергетическим разбалансом потоков энергии распространяющихся волн.

Заключение

Рассмотрено распространение электромагнитных волн прямого и обратного направлений в многослойной структуре ограниченной длины с периодической неоднородностью меандрового вида, барьеры которой обладают диссипативными свойствами. В качестве расчетного аппарата использован метод пошагового алгоритма, обобщенный на случай трехмерных электромагнитных волн, распространяющихся в среде с диссипацией.

На примере одномерной волны рассмотрено распределение амплитуд волн в слоях в случае комплексного волнового числа для барьеров. Рассмотрены два варианта соотношения составляющих волнового числа для барьера и промежутка – первый, когда действительная составляющая волнового числа для барьера значительно превышает таковую для промежутка, второй – когда действительная составляющая волнового числа для барьера равняется таковой для промежутка, а волновые числа барьера и промежутка отличаются только мнимой составляющей. Показано, что в обоих случаях наблюдаются те же основные распределения амплитуд, что и в случае без диссипации: синусоидальное и экспоненциальное.

Наряду с упомянутыми обнаружено новое распределение – линейно-синусоидальное, синусоидальный характер которого обусловлен интерференционным переотражением волн в слоях, а линейная составляющая – затуханием волны по мере удаления от источника возбуждения.

Дополнительно показано, что хотя мнимая часть волнового числа может приводить к таким же видам распределения амплитуд в слоях, что и действительная, однако главная ее роль состоит в уменьшении амплитуд волн по координате по мере удаления от источника возбуждения, которое накладывается на распределения, обусловленные действительной частью волнового числа. 

Для случая одномерной волны рассмотрены отражающие и пропускающие свойства структуры на основе зависимости от действительной части волнового числа для барьера. Показано, что при увеличении затухания общая дискретная структура спектра, то есть расположение областей пропускания и непропускания по волновому числу, в целом не меняется, тогда как прохождение волн и их отражение в соответствующих областях ухудшаются тем сильнее, чем номер области больше, причем тонкое расщепление спектра внутри областей пропускания с увеличением затухания сглаживается.

Рассмотрены основные закономерности распространения электромагнитной волны в проводящей среде. Получено волновое число и адмиттанс в виде суммы действительной и мнимой частей, в том числе в приближении большой проводимости, свойственной металлу. Рассмотрены зависимости комплексного волнового числа и адмиттанса от проводимости, получено критическое значение проводимости, при котором проводящие свойства среды начинают преобладать над диэлектрическими. Определена критическая частота, при которой в реальном металле волна затухает по амплитуде в три раза на расстоянии четверти ее длины, так что распространение волны является апериодическим.

На основе полученных результатов проведено рассмотрение распределения амплитуд волн в слоях многослойной структуры, барьеры которой обладают проводящими свойствами. Показано, что в зависимости от величины проводимости наблюдаются те же основные виды распределения амплитуд, что и для одномерной волны: синусоидальное, экспоненциальное и линейно-синусоидальное. Выполнено сравнение эффективности действия на конфигурацию распределений механизмов диссипации одномерной и электромагнитной волны. Показано, что на основе критерия сходства конфигурации  распределений механизм диссипации для электромагнитной волны является более эффективным, чем для одномерной. Однако на основе критерия подобия соотношения между действительной и мнимой частями волнового числа соотношение эффективности механизмов является обратным. Такое различие объяснено неэквивалентной ролью проводимости относительно обоих механизмов, так как для обеспечения подобия конфигурации распределений проводимость должна значительно превышать значение, требуемое для подобия волновых чисел.

Рассмотрены отражающие и пропускающие свойства структуры для электромагнитной волны. Показано, что частотная зависимость упомянутых свойств, в основном, подобна зависимости от волнового числа для одномерной волны, то есть имеет сходный дискретный характер, однако здесь при увеличении номера области непропускания максимальная амплитуда волн в слоях преимущественно сохраняется. Показано, что положение областей непропускания от проводимости в пределах ее средних значений от частоты не зависит, то есть подчиняется тому же закону соответствия суммы длин барьера и промежутка нечетному числу четвертей длины волны, что и для бездиссипативной среды.

Исследована частотная конфигурация отдельной области непропускания, показано, что как и для бездиссипативной структуры, область представляет собой широкий центральный лепесток, окруженный узкими сателлитами спадающей амплитуды. Однако по мере увеличения проводимости тонкая структура сателлитов сглаживается, уступая место достаточно гладкому распределению.

В высокочастотной части области непропускания обнаружен обусловленный проводимостью диссипативный резонанс, а также некоторое превышение потока энергии отраженной волны по сравнению с падающей. В качестве возможного объяснения подобной аномалии рассмотрены известные механизмы такого превышения, причем отдано предпочтение механизму, учитывающему локализацию энергии во внутренних слоях структуры в виде совокупности активной и реактивной составляющих.   

Рассмотрено распространение электромагнитных волн в периодических структурах, барьеры которых обладают металлической проводимостью. Показано, что при этом в формировании распределений амплитуд, отличных от чисто экспоненциального, таких как синусоидальное и линейное, необходимым условием является превышение глубины проникновения волны над толщиной барьера, тогда как полная толщина структуры может превышать глубину проникновения более чем на порядок. Показано, что амплитуды отраженных и проходящих волн относительно структуры в целом при повышении частоты уменьшаются вплоть до толщин, составляющих четвертую-пятую часть от глубины проникновения волны в металл, а при меньших толщинах испытывают аномальное увеличение, в качестве возможного способа устранения которого указан учет локализации энергии волны в виде совокупности активной и реактивной составляющих.   

 

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

 

Литература

    1. Антонец И.В., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2015. №2.
URL: http://jre.cplire.ru/jre/feb15/1/text.html (первая часть настоящей работы).  

    2. Антонец И.В., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2015. №2.
 URL: http://jre.cplire.ru/jre/feb15/2/text.html (вторая часть настоящей работы).  

    3. Антонец И.В., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2015. №3.

URL: http://jre.cplire.ru/jre/mar15/13/text.html (третья часть настоящей работы).  

    4. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №1. С.67.

    5. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №1. С.16.

    6. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №1.
URL: http://jre.cplire.ru/jre/jan13/11/text.pdf.

    7. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть пятая. Алгоритмические методы. Сыктывкар: ИПО СыктГУ. 2014.  

    8. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос. Изд. физ.-мат. лит. 1960. 

    9. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.

    10. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.

    11. Gilbert T.L. // IEEE Trans. on Magn. 2004. V.40. №6. P.3443.

    12. Стрелков С.П. Введение в теорию колебаний. М.: Наука. 1964.

    13. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука. 1978.

    14. Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: Физматлит. 2003.

    15. Никольский В.В, Никольская Т.И. Электродинамика и  распространение радиоволн. М.: Наука. 1989.

    16. Левич В.Г. Курс теоретической физики. Т.1. М.: Наука. 1969.

    17. Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. М.: Высшая школа. 1974.

    18. Корн Г., Корн Т.  Справочник по математике для научных работников и инженеров. М.: Наука. 1973.

    19. Лакс Б., Баттон К. Сверхвысокочастотные ферриты и ферримагнетики. М.: Мир. 1965. 

    20. Вашковский А.В., Стальмахов В.С., Шараевский Ю.П.  Магнитостатические волны в электронике сверхвысоких частот. Саратов: Изд.Саратовского университета. 1993.

    21. Вамберский М.В., Абрамов В.П., Казанцев В.И. Конструирование ферритовых развязывающих приборов СВЧ. М.: Радио и связь. 1982.

    22. Вендик И.Б., Вендик О.Г. // ЖТФ. 2013. Т.83. №1. С.3.

    23. Вендик О.Г., Калиникос Б.А. // Изв. ВУЗов. Физика. 1988. Т.31. №11. С.3.

    24. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2008. Т.53. №8. С.901.

    25. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред (Теоретическая физика, т.VIII). М.: Наука. 1982.

    26. Вайнштейн Л.А. // Электромагнитные волны. М.: Сов. радио. 1957.  

    27. Гороновский И.Т., Назаренко Ю.П., Некряч Е.Ф. Краткий справочник по химии. Киев: Наукова думка. 1974.

    28. Кизель В.А. Отражение света. М.: Наука. 1973.

    29. Веремей В.В., Горбунова Т.А., Пуговкин Л.В. // Оптика и спектроскопия. 1978. Т.44. №2. С.345.

    30. Бойко Б.Б., Лещенко В.Г., Петров Н.С. // Ковариантные методы в теоретической физике. Оптика и акустика. Сборник научных трудов. Вып.1. Минск: Изд. ИФ АН БССР. 1981. С.40.

    31. Джилавдари И.З., Филиппов В.В. // ЖПС. 1981. Т.35. №1. С.152.

    32. Минков И.М. // Оптика и спектроскопия. 1985. Т.58. №2. С.466.

    33. Ефимов В.В., Семенцов Д.И. // ЖТФ. 1997. Т.67. № 2. С.118.

    34. Афанасьев С.А., Семенцов Д.И. // УФН. 2008. Т.178. №4. С.377.

    35. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №10. С.1171.

    36. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XVI Международной конференции "Радиолокация и радиосвязь". Москва: НИУ МЭИ. 2008. С.18.

    37. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов IX Международного семинара “Магнитные фазовые переходы”. Махачкала: издание Института физики Дагестанского научного центра РАН. 2009. С.67.

    38. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции “Новое в магнетизме и магнитных материалах (НМММ)”. Москва: Изд-во МГУ. 2009. С.939.

    39. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XIX Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2011. С.166.

    40. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // "XXXIV Международная зимняя школа физиков-теоретиков - Коуровка 2012". Тезисы докладов. Екатеринбург: ИФМ УрО РАН.  2012. С.101.

    41. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XX Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2012. С.215.

    42. Антонец И.В., Котов Л.Н., Некипелов С.В., Шавров В.Г., Щеглов В.И. // РЭ. 2004. Т.49. №10. С.1243.

    43. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. //  РЭ. 2006. Т.51. №12. С.1481.

    44. Казанцева Н.Е., Пономаренко А.Т., Шевченко В.Г., Чмутин И.А., Калинин Ю.Е., Ситников А.В. // Физика и химия обработки материалов. 2002. №1. C.5.

    45. Калинин Ю.Е., Ремизов А.Н., Ситников А.В. // ФТТ. 2004. T.46. №11. C.2076.

    46. Иванов А.В., Калинин Ю.Е., Нечаев А.В., Ситников А.В. //

ФТТ. 2009. T.51. №12. C.2331.

    47. Ситников А.В. Электрические и магнитные свойства наногетерогенных систем металл-диэлектрик. Диссертация на соискание ученой степени докт. физ.-мат. наук. Воронеж: ВГТУ. 2010.

    48. Антонец И.В., Котов Л.Н., Калинин Ю.Е., Ситников А.В., Шавров В.Г., Щеглов В.И. // ПЖТФ. 2014. Т.40. №14. С.1.