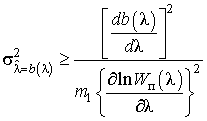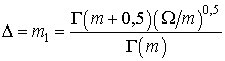УДК 681.3

Оценка погрешности измерения скалярного информационного параметра сигнала
на фоне мультипликативных помех

 

В. М. Артюшенко¹, В. И. Воловач²

¹ГБОУ ВО МО «Технологический университет», г. Королев

²ФГБОУ ВПО «Поволжский государственный университет сервиса», г. Тольятти

 

Статья поступила в редакцию  1 марта 2016 г.

 

Аннотация. В статье рассматривается оценка погрешности измерения скалярного информационного параметра полезного сигнала на фоне мультипликативных негауссовских помех. Для оценки информационных параметров сигнала используются метод максимума апостериорной плотности распределения вероятности, а также нижние границы неравенства Рао-Крамера. Показано, что воздействие мультипликативной помехи на полезный сигнал в общем случае приводит к смещению оценки измеряемых параметров. Показано, что при известных параметрах распределения мультипликативной помехи можно определить вносимую ей величину смещения и перейти несмещенной оценке. Показано, что точность измерения параметров движения возрастает с увеличением отличия плотности распределения вероятности оцениваемого параметра и воздействующей мультипликативной помехи от гауссовской.

Ключевые слова: радиолокационный измеритель, мультипликативная негауссовская помеха, смещение оценки, отношение сигнал/помеха, погрешность измерения.

Abstract. In the article the estimation of error of measurement scalar information parameter of the useful signal along with the non-Gaussian multiplicative noise is considered. To estimate the information parameters of the signal we use the method of maximum a posteriori probability density and lower bounds of Rao-Cramer inequality. It is shown that in general case the impact of multiplicative noise on the useful signal leads to shift of estimates of measured parameters. It is shown that with known distribution parameters of the multiplicative noise we can determine the shift value and get to an unbiased estimate. It is shown that the accuracy of the measurement of motion parameters increases with the difference of the density of the probability distribution of the estimated parameter and influence of multiplicative noise of Gaussian noise.

Key words: radar meter, multiplicative non-Gaussian noise, displacement estimates, signal/interference ratio, measurement error.

Введение

В радиолокации вопросы измерения (оценки) параметров сигналов, несущих информацию о лоцируемых объектах (целях), в том числе о параметрах их движения, являются традиционными и весьма подробно рассмотрены в [1, 2, 3 и др.]. Достаточно хорошо изучены вопросы радиолокационного измерения параметров точечных [4, 5], а также отчасти и сложных дискретных [6, 7] целей. Вместе с тем многие аспекты, связанные с измерением информационных параметров полезного сигнала об объектах, находящихся на относительно небольших расстояниях от радиолокационных измерителей, являются изученными в недостаточной степени и имеют ряд специфических особенностей как теоретического, так и практического характера [8-12], обусловленных работой измерителей в условиях ближнего действия.

Отметим, что в большинстве работ, посвященных вопросам оценки параметров сигналов, считалось, что на последний воздействуют только аддитивные помехи, описывающеюся, как правило, гауссовской плотностью распределения вероятности (ПРВ). Вместе с тем, как показывают проведенные исследования [13-19], принимаемый измерителем сигнал подвержен воздействию не только со стороны аддитивных, но и мультипликативных помех, имеющих ярко выраженный негауссовский характер. Для радиолокации, радионавигации, телеметрии, радиоизмерительной техники представляет значительный интерес оценить влияние мультипликативной помехи на точность измерения параметров движения протяженных объектов.

Оценка погрешности измерения информационных параметров в условиях воздействия мультипликативных негауссовских помех

Задачу оценивания информационных параметров полезного сигнала будем решать в дискретном времени наблюдения. Считаем, что в течение времени [0, T] наблюдается выборки случайного процесса  (h = 1, …, H), являющегося смесью полезного сигнала   и мультипликативной  помехи. Полезный сигнал содержит совокупность параметров , подлежащих измерению (оцениванию), причем считается, что на интервале наблюдения эти параметры остаются неизменными. Оценку информационных параметров будем осуществлять по методу максимума апостериорной ПРВ (АПРВ).

Для определения количественных оценок измеряемых параметров используем нижние границы неравенства Крамера-Рао [20, 21].

Отметим, что в нашем случае оценке будут подлежать только неэнергетические информационные параметры полезного сигнала. При этом считается, что оценки параметров асимптотически (при ) состоятельны, эффективны и нормально распределены [22, 23].

Как известно [24-26], воздействие мультипликативной помехи на полезный сигнал приводит, в общем случае, к смещению оценки измеряемых (оцениваемых) параметров. В этом случае математическое ожидание оценки информационного параметра будет смещено относительно l:

,

где  – оценка информационного параметра l;  – функция правдоподобия, зависящая как от параметра l, так и от реализации ; (), наблюдаемого случайного процесса;  – смещение оценки.

Дисперсия смещенной оценки находится как:

.

 

Нижняя граница дисперсии смещенной оценки, определяемая неравенством Крамера-Рао, в этом случае будет иметь вид [1, 21]:

,                                         (1)

где .

Следует отметить, что, как правило, для смещенной оценки информационного параметра ее точность определяется не дисперсией, а среднеквадратическим отклонением (СКО) от оцениваемого параметра l [1, 21]:

.

 

Данное выражение показывает полную ошибку измерения (оценивания) информационного параметра, учитывающую смещение оценки, вызванное мультипликативной помехой.

В большинстве случаев определить величину смещения достаточно сложно. Обычно для этого применяют метод вариационного исчисления [27, 28].

Сравнительно просто определить смещение лишь в том случае, если само смещение не зависит от оцениваемого параметра . В этом случае при определении нижних границ неравенства Крамера-Рао можно перейти к несмещенной оценке информационного параметра  [1].

В качестве примера определим величину смещения, вызываемую воздействием на полезный сигнал  мультипликативной помехи , описываемой ПРВ Накагами:

, ,                (2)

где: ,  – параметры распределения; Г(.)– гамма-функция.

 

Считаем, что помеха и оцениваемый параметр между собой независимы. В этом случае величина смещения определяется математическим ожиданием модулирующей помехи и будет зависеть лишь от параметров ее распределения  [29]:

.                                 (3)

Отметим, что параметр распределения m в этом случае может служить мерой глубины флюктуаций интенсивности мультипликативной помехи, определяемый как отношение квадрата средней мощности воздействующей помехи  к ее дисперсии [30, 31]:

,

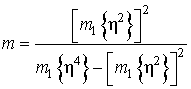где  – начальный момент n-го порядка интенсивности мультипликативной помехи.

 

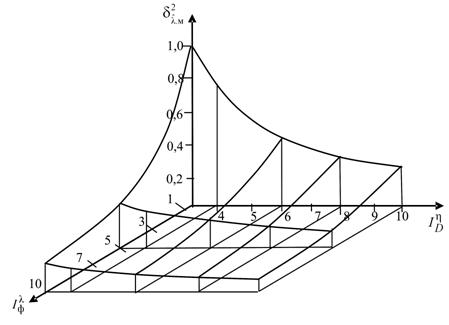
Рис. 1. Зависимости величины смещения Δ от параметров мультипликативной помехи m и Ω, описываемой ПВР Накагами

 

Как видно из выражения (3) и приведенных графиков, с увеличением параметра Ω, характеризующего среднюю мощность мультипликативной помехи, величина смещения так же возрастает. При изменении глубины флюктуации интенсивности мультипликативной помехи, определяемой значением параметра m, в диапазоне от 0,5 до 1 смещение практически не меняется. Таким образом, если известны параметры распределения мультипликативной помехи, то можно определить вносимую ею величину смещения, после чего, как это было показано выше, если смещение не зависит от оцениваемого параметра, легко перейти к несмещенной оценке информационного параметра.

Оценка погрешности измерения скалярного информационного параметра на фоне мультипликативной помехи с независимыми значениями

Конкретизируем оценку точности измерения параметров движения лоцируемого объекта в условиях мультипликативных негауссовских помех, имеющих независимый характер.

Считаем, что на вход радиолокационного измерителя поступает мультипликативная смесь вида полезного сигнала  несущего информацию, например, об одном из параметров движения объекта – скорости, ускорении и др. –  и мультипликативной негауссовской помехи . Логарифм функции правдоподобия (ЛФП)  существует и может быть записан относительно мультипликативной помехи в виде [20]:

,

где  – ПРВ мультипликативной негауссовской помехи с независимыми значениями.

Воспользовавшись методикой изложенной в [20], пропуская довольно громоздкие математические преобразования, приведенные подробно в [26], получим:

,

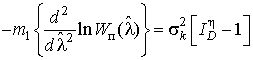где

;

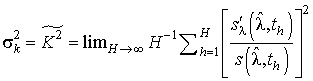k – коэффициент, учитывающий форму полезного сигнала;

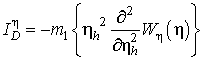 – Фишеровская дисперсионная информация (динформация) [32], заключенная относительно мультипликативной помехи в одномерной ПРВ .

Неравенство Крамера-Рао (1) при оценке параметра l по максимуму апостериорной ПРВ, с учетом выше сказанного, будет определяться:

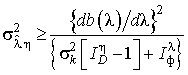,                                      (4)

где  – информация по Фишеру, содержащаяся в случайном процессе с одномерной ПРВ : .

 

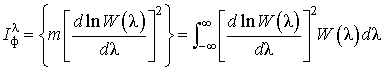Заметим, что в случае несмещенной оценки информационного параметра l, при воздействии на полезный сигнал мультипликативной помехи выражение (4) примет вид:

.                                   (5)

 

Если оценка информационного параметра осуществляется методом максимального правдоподобия, то (5) запишется:

.                                         (6)

 

Осуществим количественную оценку повышения точности измерения информационного параметра за счет учета негауссовского характера распределения, как самого измеряемого процесса, так и воздействующей мультипликативной помехи.

Для удобства оценки получаемого выигрыша построим зависимости для приведенной дисперсии оценки информационного параметра

,

где  – дисперсия погрешности, рассчитанная при измерении (оценки) гауссовского информационного параметра при воздействии мультипликативной помехи с независимыми значениями, описываемой одномерной, односторонней гауссовской ПРВ. Отметим, что для случайного процесса с гауссовской ПРВ , а  [30].

Для упрощения расчетов с сохранением полученных результатов примем, что , а оценка измеряемого информационного параметра является несмещенной. На рис. 2 приведены графики зависимости .

 

Рис. 2. Зависимость приведенной дисперсии оценки  информационного параметра сигнала от  и

 

Из представленных графиков и выражения (5) видно, что точность измерения (оценки) информационного параметра возрастает с увеличением отличия ПРВ оцениваемого параметра и воздействующей мультипликативной помехи от гауссовской. При этом выигрыш в точности измерения (оценки) при наличии канала оценки мультипликативной помехи может иметь существенный характер. Так, при  потенциальная точность измерения увеличивается в два раза.

Проанализируем более подробно, как влияет учет негауссовского характера воздействующей мультипликативной помехи на точность измерения информационного параметра.

В качестве примера рассмотрим случай измерения (оценки) фазы фазомодулированного (ФМ) полезного сигнала

,

где  – коэффициент фазовой модуляции, при воздействии мультипликативной помехи , описывающейся одномерной ПРВ Накагами (2).

Считаем, что флюктуация амплитуды не зависит от флюктуации фазы, причем флюктуация фазы носит симметричный характер. В этом случае, согласно [28], оценка фазы  имеет несмещенный характер. Осуществим оценку фазы методом максимального правдоподобия.

Воспользовавшись результатами, полученными в [26], с учетом (2), после необходимых преобразований, получим выражение Фишеровской дисперсионной информации, которая в этом случае будет иметь вид:

,

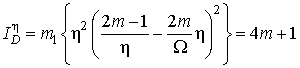где m и  – параметры распределения Накагами.

Учитывая, что составляющие двойной радиочастоты в измерителе отфильтровываются, проведя усреднение ФМ сигнала, получим:

.

Подставив найденное выражение в (6), запишем окончательное выражение для неравенства Крамера-Рао

.                                                (7)

Заметим, что в данном случае произведение  играет роль отношения сигнал/помеха (ОСП).

Как видно из представленного неравенства при , , то есть с увеличением ОСП точность оценки измерения фазы возрастает, что полностью совпадает с известными результатами [20].

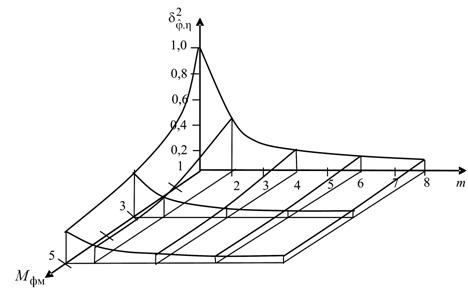
На рис. 3 представлены зависимости  приведенной погрешности измерения фазы ФМ сигнала .

 

Рис. 3. Зависимость приведенной погрешности оценки фазы  сигнала от параметров  и m

 

Здесь  – нижняя граница погрешности измерения фазы сигнала при воздействии мультипликативной помехи с ПРВ Накагами, когда параметр   (ПРВ Накагами переходит в ПРВ Релея).

Из неравенства (7) и представленных графиков видно, что чем больше ПРВ мультипликативной помехи отличается от Релеевской, тем более точно можно оценить фазу полезного сигнала.

Отметим, что с ростом величины фазовой модуляции  точность измерения (оценки) также возрастает.

Выводы

Таким образом, определены граничные значения неравенства Крамера-Рао для совместной и раздельной оценки информационных параметров полезного сигнала на фоне мультипликативных помех. Показано, что в общем случае мультипликативная помеха ведет к смещению оцениваемых информационных параметров, причем, чем больше величина смещения, тем точность измерения хуже. Учет смещения, вызванный модулирующей помехой, позволяет перейти к несмещенным оценкам. Показано, что погрешность измерения скалярного информационного параметра полезного сигнала на фоне мультипликативной помехи с независимыми значениями может быть существенно уменьшена за счет учета Фишеровской дисперсионной информации (динформации)  о модулирующей помехе.

Работа выполнена в рамках фундаментальной НИР, финансируемой из средств Минобрнауки РФ (Государственное задание на 2014, 2015 гг., № ГР 01201458513).

Литература

1. Сосулин Ю. Г. Теоретические основы радиолокации и радионавигации: учеб. пособие для вузов. М.: Радио и связь, 1992. 304 с.

2. Финкельштейн М. И. Основы радиолокации. М.: Радио и связь, 1983. 536 с.

3. Radar handbook / Ed. by M. I. Scolnik; 2nd ed. New York: McGraw-Hill, 1990. 1199 p.

4. Родимов А. П., Поповских В. В. Статистическая теория поляризационно-временной обработки сигналов и помех. М.: Радио и связь, 1984. 272 с.

5. Nebabin V. G. Methods and Techniques of Radar Recognition. Boston – Lo ndon: Artech House, 1994. 273 p.

6.  Радиолокационные характеристики летательных аппаратов / М. Е. Марганов, Ю. С. Зиновьев, Л. Ю. Астанин и др.; под ред. Л. Т. Тучкова. М.: Радио и связь, 1985. 236 с.

7. Фалькович С. Е., Хомяков Э. Н. Статистическая теория измерительных радиосистем. М.: Сов. радио, 1981. 288 c.

8. Komarov I. V., Smolskiy S. M. Fundamentals of short-range FM radar. Norwood: Artech House, 2003. 289 p.

9. Артюшенко В. М., Воловач В. И. Оценка погрешности измерения параметров движения протяженных объектов в условиях изменяющейся дальности // Известия вузов. Радиоэлектроника. 2015. Т. 58. № 1. С. 26-37.

10. Воловач В. И. Методы и алгоритмы анализа радиотехнических устройств ближнего действия. М.: Радио и связь, 2013. 228 с.

11. Hammarstrand L., Svensson L., Sandblom F., Sorstedt J. Extended object tracking using a radar resolution model // IEEE Trans. Aerosp. Electron. Syst. July 2012. Vol. 48. No. 3. P. 2371-2386.

12. Hughes P. K. A high-resolution radar detection strategy // IEEE Trans. Aerosp. Electron. Syst. Sept.1983. Vol. 19. No. 5. P. 663-667.

13. Артюшенко В. М., Воловач В. И. The estimation of measurement accuracy of information parameters of the signal along with the correlated additive noise under continuous processing // Успехи современной радиоэлектроники. 2015. № 8. С. 80-89. (in English).

14. Артюшенко В. М., Воловач В. И. Analysis of influence of additive non-Gaussian noise on accuracy of motion parameters measurement in short-range radio systems // Нелинейный мир. 2015. Т. 13. № 1. С. 16-30. (in English).

15. Артюшенко В. М., Воловач В. И. Оценка погрешности измерения скалярного информационного параметра движущегося протяженного объекта на фоне аддитивных негауссовских помех // Журнал радиоэлектроники. 2015. № 1. С. 4. [Электронный ресурс]. URL: http://jre.cplire.ru/jre/jan15/12/text.html

16. Артюшенко В. М., Воловач В. И. Оценка погрешности измерения векторного информационного параметра сигнала на фоне аддитивных некоррелированных негауссовских помех // Журнал радиоэлектроники. № 1, 2016. С. 6. [Электронный ресурс]. URL: http://jre.cplire.ru/jre/jan16/6/text.html

17. Kassam S. A. Signal Detection in Non-Gaussian Noise. New York: Springer Verlag, 1989. 242 p.

18. Lu N. H., Eisenstein Bruce A. Detection of weak signals in non-Gaussian noise // IEEE Trans. Microwave Theory Tech. Nov. 1981. Vol. 27. No. 6. P. 755-771.

19. Теория обнаружения сигналов / П. С. Акимов, П. А. Бакут, В. А. Богданович и др.; под ред.  П. А. Бакута. М.: Радио и связь, 1984. 440 с.

20. Тихонов В. И., Кульман Н. К. Нелинейная фильтрация и квазикогерентный приём сигналов. М.: Сов. радио, 1975. 704 c.

21. Левин Б. Р. Теоретические основы статической радиотехники / 3-е изд., перераб. и доп. М.: Сов. радио, 1989. 656 с.

22. Тихонов В. И., Харисов В. Н. Статистический анализ и синтез радиотехнических устройств и систем: учеб. пособие для вузов. М.: Радио и связь, 1991. 608 с.

23. Крамер Г. Математические методы статистики / пер. с англ.; под ред. А. Н. Колмогорова. М.: Мир, 1975. 648 с.

24. Модулирующие (мультипликативные) помехи и прием радиосигналов / И. Я. Кремер, В. И. Владимиров, В. И. Карпухин ; под ред. И. Я. Кремера. М.: Сов. радио, 1972. 480 с.

25. Васильев К. К. Прием сигналов при мультипликативных помехах. Саратов:  Изд-во Саратовского Ун-та, 1983. 128 с.

26. Артюшенко В. М. Обработка информационных параметров сигнала в условиях аддитивно-мультипликативных негауссовских помех. М.: ФГБОУ ВПО ФТА; изд-во «Канцлер», 2014. 298 с.

27. Бакут П. А., Логинов В. П., Шумилов Ю. П. Методы определения границ точности в задачах оценивания неизвестных параметров // Зарубежная радиоэлектроника. 1978. № 5. С. 3-36.

28. Tzay Y. Yong, Westerberg R. A. Error bounds for stochastic estimation of signal parameters // IEEE Trans. on Information Theory. Sept. 1971. Vol. 17. No. 5. P. 549-557.

29. Nakagami M. The m-distribution-A-general formula of intensity of rapid fading // Statistical Methods in Radio Wave Propagation: Proceedings of a Symposium Held at the University of California, Los Angeles, June 18-20, 1958. New York : Pergamon Press, 1960. РР. 3-36.

30. Билетов М. В., Вассерштейн И. С., Рыльский В. В. Обнаружение радиолокационных сигналов при флуктуациях их интенсивности по закону Накагами // Радиотехника. 1976. Т. 31. №1. С.16-19.

31. Долуханов М. П. Флуктуационные процессы при распространении радиосвязи. М.: Связь, 1971. 360 с.

32. Цыпкин Я. З. Основы информационной теории идентификации. М.: Наука, 1984. 320 с.