Метод импедансного аналога электромагнитного пространства для решения трехмерных векторных задач электродинамики
С.А. Иванов*, Б.В. Сестрорецкий**, А.Н. Боголюбов**Физический факультет МГУ им. М.В. Ломономова
**ФГУП НПО им. С.А. ЛавочкинаПолучена 19 мая 2008 г.
Подробно изложены основные положения метода импедансного аналога электромагнитного пространства, предназначенного для численного решения двух- и трехмерных задач электродинамики во временной и частотной областях. Рассмотрены некоторые теоретические результаты и практические приложения для трехмерных задач.
Введение
В настоящем обзоре изложены основные положения эффективного сеточного метода расчета электродинамических систем и устройств СВЧ, известного как метод импедансного аналога электромагнитного пространства (ИАЭП) [1-4]. Данный метод является логическим продолжением метода электрических сеток, основателем которого является советский математик С.А. Гершгорин, разработавший в 1927 г. основы построения сеточных моделей [5]. В своей пионерской работе С.А. Гершгорин предложил использовать сетку из сопротивлений для экспериментального решения уравнения Лапласа. Серия работ С.А. Гершгорина привела к возникновению нового класса аналоговых вычислительных машин – электроинтеграторов сеточного типа [6], которые весьма продуктивно использовались вплоть 70-х годов 20-го века [6-8]. Сеточные электроинтеграторы уже в 30-х годах прошлого столетия позволяли исследовать системы, содержащие более миллиона ячеек – рекорд, превзойденный цифровыми ЭВМ менее 15 лет назад.
Большой вклад в развитие сеточных методов внес американский ученый и инженер Габриэль Крон [9, 10]. Именно он впервые предложил радиотехническую модель уравнений Максвелла [9]. К сожалению, полная трехмерная модель оказалась ошибочной, однако для двумерных задач модели были правильные. Метод, названный автором диакоптикой, несмотря на свою глубину, оказался весьма труден для восприятия, и поэтому широкого распространения не получил.
В начале 70-х годов методы радиотехнических аналогий пережили новое рождение. В Советском Союзе благодаря работам Б.В. Сестрорецкого 1967-74 гг. появился метод импедансного аналога электромагнитного пространства. Западный метод, предложенный П. Джонсом в 1971 г., получил название TLM, или метод матриц линий передач [11-13].
Первые теоретические и практические исследования метода ИАЭП относятся к 1967-74 гг. [1, 2, 14]. Достигнутый к настоящему времени уровень программ, реализующих различные идеи метода ИАЭП, позволяет проектировать сложные волноведущие системы без экспериментальной доводки образцов, поскольку точность программ зачастую превышает возможности измерительной аппаратуры.
Методология метода ИАЭП позволяет строить точные и быстрые алгоритмы анализа достаточно сложных физических систем. Для примера: в проектируемой установке ITER требуется анализировать отраженные сигналы от высокотемпературной плазмы сечением до 500x500 длин волн при учете, что плазма может иметь отрицательные значения диэлектрической постоянной. В результате длительных исследований была создана программа TAMIC Rt-H Planar [15]. Результаты расчетов по этой программе в Курчатовском институте, представленные в 2003 году на международном совещании по диагностике ITER, произвели большое впечатление и показали, что код практически не имеет конкурентов по решаемым объемам и скорости счета.
Основы метода ИАЭП
Метод ИАЭП относится к классу сеточных численных методов, однако, в отличие от метода конечных разностей и метода конечных элементов, базируется на существенно отличной методологии построения вычислительных алгоритмов. Согласно данной методологии при решении любой задачи математической физики выделяется важный этап, предшествующий строгой постановке задачи, – построение эквивалентной радиотехнической схемы устройства (см. рис. 1).

Рис. 1. Волноводное устройство (а) и его эквивалентная радиотехническая схема (б).
В случае, когда речь идет об электродинамике, эквивалентная радиотехническая схема устройства – это такая радиотехническая схема, процессы в которой близки в некотором смысле к электромагнитным процессам в реальном объекте. Возбуждая одну и ту же эквивалентную схему сигналами различной формы, можно решать различные задачи математической физики, сводя исходную задачу к задаче теории цепей. Поэтому можно сказать, что эквивалентная схема устройства является радиотехническим, или импедансным, аналогом реального физического объекта. При таком подходе процедуры постановки и решения задач математической физики существенно вторичны по отношению к процедурам построения эквивалентных схем, поскольку последние обладают значительно большей общностью.
Базовой концепцией метода является концепция дискретного сеточного вакуума [3, 16]. Благодаря этой концепции и происходит смещение акцентов от решения задач математической физики к построению эквивалентных схем. Для этого вводится понятие дискретного сеточного вакуума, или эквивалентной схемы пустого пространства, основное предназначение которого – достаточно точно описывать плоские волны. Строится сеточный вакуум следующим образом: непрерывное пустое пространство регулярным образом разбивается на одинаковые элементарные объемы, каждому элементарному объему сопоставляется его эквивалентная радиотехническая схема, после чего эквивалентные схемы элементарных объемов объединяются в единую схему – дискретный сеточный вакуум.
Различают два вида схем: RLC-схемы с сосредоточенными элементами, применяемые для расчета в частотной области, и универсальные R
-схемы с распределенными параметрами, которые могут исследоваться как в частотной, так и во временной области. Эквивалентные радиотехнические RLC- и R
-схемы устройств (в т.ч. вакуума) называются также импедансными RLC- и R
-сетками. Отметим, что RLC- и R
-сетки всегда консервативны (как радиотехнические схемы), т.е. для них выполняется закон сохранения электромагнитной энергии (естественно, при отсутствии потерь в веществе). Простейшие эквивалентные двумерные схемы элементарного объема приведены на рис. 2а и 2б. Данные схемы применяются соответственно для решения краевых задач для уравнения Гельмгольца и начально-краевых задач для волнового уравнения.

Рис. 2. Эквивалентные схемы элемента пространства: а) RLC-схема, б) R-схема.
Для построения эквивалентных схем элементарных объемов могут использоваться как классические приемы [17], так и приемы, непосредственно разработанные в рамках ИАЭП [15, 16]. Среди последних укажем “концепцию виртуальных TEM-волноводов”, называемую также “концепцией плоских волн” [18, 19]. Согласно последней эквивалентная схема элементарного объема собирается из отдельных LC-цепочек или отрезков линий передачи, моделирующих одномерные TEM-волноводы. При таком подходе не только дискретный сеточный вакуум, но и эквивалентная схема элементарного объема строятся исходя из интегральных представлений, т.е. представлений о решениях спектральной задачи для пустого пространства.
Для количественного описания точности дискретного сеточного вакуума введено понятие сеточной дисперсии [3, 16, 20]. Основные типы сеточной дисперсии следующие. Фазовая (амплитудная) сеточная дисперсия – это зависимость фазовой скорости (характеристического сопротивления) плоской сеточной волны от направления волнового вектора. Понятие сеточной дисперсии по сути является интегральным аналогом аппроксимации, но выгодно отличается от последней большим количеством описываемых параметров и тем, что базируется на описании точных решений, а не функций более широкого класса.
Таким образом, сеточный вакуум последовательно строится как дискретный радиотехнический аналог пустого непрерывного электромагнитного пространства, причем в понятие аналогии вкладывается близость электромагнитных процессов, происходящих в этих объектах. Отметим, что это построение происходит до постановки задачи математической физики, и получаемая схема сеточного вакуума, вообще говоря, не зависит даже от класса вышеуказанной задачи.
Эта же идея используется и при построении радиотехнических аналогов более сложных объектов. Свойства вещества, “погруженного” в сетку вакуума, учитываются дополнительными реактивными двухполюсниками, которые “навешиваются” на пары клемм вакуумной сетки. В RLC-схемах для этих целей используются емкости и индуктивности, в R
-схемах – короткозамкнутые и разомкнутые шлейфы. Если вводимое вещество поглощает или генерирует СВЧ энергию, то в “навешиваемые” двухполюсники вводятся сопротивления и источники ЭДС.
Границы исследуемой системы описываются аналогичным образом RLC- и R
-схемами. Для систем со сложной геометрией может производиться сгущение и изменение формы элементарных объемов сетки.
Расчет устройств может вестись как на конечных, так и на бесконечных сетках. Для каждого случая построение эквивалентной схемы устройства, вопросы возбуждения и поглощения электромагнитной энергии имеют свои особенности. В данном обзоре представлены только конечные сетки. Бесконечные сетки рассмотрены в работах [21, 22].
Трехмерные эквивалентные схемы
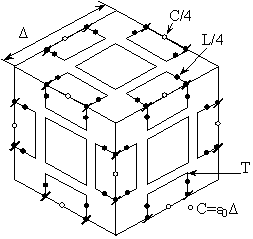
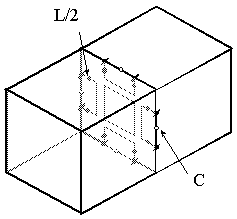
Для построения трехмерного сеточного вакуума, предназначенного для анализа трехмерных векторных задач в полной электродинамике, были предложены две эквивалентные схемы элементарных объемов – т.н. 12-входовые элементы роторного [18] (рис. 3а) и потокового [19] типов (рис. 3б).

Рис. 3. Размещение пар клемм на ребрах элемента роторного типа (а) и ортогональных пар клемм в центрах граней элемента потокового типа (б) для элементарного объема кубической формы
.
У роторного элемента входы (пары клемм) располагаются на ребрах элементарного объема
с ориентацией электрического поля по линии ребер (круг обозначает пару клемм, черта, пересекающая круг – ориентацию электрического поля). У потокового элемента входы (по две пары клемм с ортогональными поляризациями электрического поля) размещаются в центрах каждой грани куба.
Рис. 4. LC-схема грани роторного кубика.LC-схема роторного элемента состоит из шести одинаковых LC-схем рис. 4, расположенных на гранях элементарного объема
(на этом и следующих рисунках черными кружками обозначены индуктивности, белыми – емкости). Каждая такая схема представляет собой симметричный 8-полюсник: четыре LC-цепочки, связанные между собой идеальным симметрирующим трансформатором. Основная функция трансформатора – обеспечение равенства токов во всех четырех плечах. Полная LC-схема роторного кубика получается объединением шести описанных схем в одну: 8-полюсники размещаются на гранях элемента, входы 8-полюсников, расположенные на одном ребре, объединяются параллельно. Полная LC-схема роторного оператора приведена на рис. 5.
Рис. 5. Эквивалентная LC-схема роторного элемента.
Таким образом, у роторного элемента получаем 12 входов (по числу ребер). Отметим, что роторная схема рис. 5 отличается от схемы кубика Крона наличием симметрирующих трансформаторов. Именно они обеспечивают равенство токов во всех четырех плечах на одной грани элементарного объема, и, таким образом, энергетическую эквивалентность роторной схемы уравнениям Максвелла.
Объединение отдельных кубиков в единую сетку происходит с помощью слияния одинаковых LC-схем, расположенных на гранях элементарных объемов (см. рис. 6). При этом индуктивности и емкости подключаются параллельно друг к другу, т.е. получаем уменьшение индуктивностей вдвое и увеличение емкостей вчетверо.
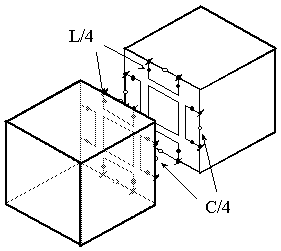
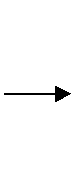
Рис. 6. Объединение отдельных кубиков в единую сетку.
R
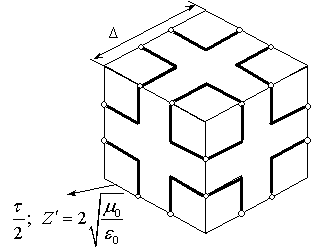
-схема роторного кубика (см. рис. 7) получается из его LC-схемы на основе эквивалентности LC-схемы рис. 8а и короткого отрезка идеальной двухпроводной линии рис. 8б. R
-схема также состоит из шести 8-полюсников, расположенных на гранях кубика. 8-полюсники в свою очередь являются последовательными узлами, состоящими из четырех одинаковых линий передач с временной задержкой
, где с – скорость света в вакууме,
– длина ребер роторного кубика,
– временной шаг.
Рис. 7. Эквивалентная R-схема роторного элемента.
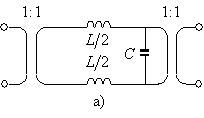
Рис. 8. Преобразование LC-схемы (а) в отрезок линии передач (б) с волновым сопротивлением
и временем задержки
.
Алгоритм расчета роторной R
-сетки может быть легко сформулирован в терминах токов и напряжений [16, 18] и является аналогом консервативного варианта конечно-разностной схемы метода FDTD. Для расчета по данному алгоритму требуется хранить 6 параметров на один элемент (три напряжения и три тока) и использовать 27 операций на один временной такт
.
Вещество моделируется подключением дополнительных двухполюсников к сетке вакуума. Модифицированная R
-схема роторного кубика для случая
и
приведены на рис. 9.
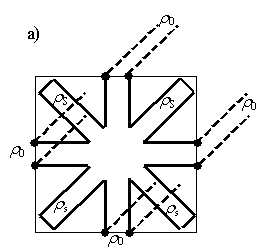
Рис. 9. Эквивалентные модифицированные схемы роторного кубика: а) одной грани; б) роторного кубика в целом.
Эквивалентные схемы потокового элемента (ПЭ) можно построить несколькими способами [16, 19]. Наиболее просто LC- и R
-схемы ПЭ получаются с помощью модификации соответствующих схем роторного элемента. Для этого требуется переместить схемы, расположенные на гранях роторного кубика в плоскости его симметрии (см. рис. 10).
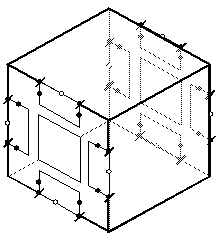
Рис. 10. Перемещение LC-схем граней в центр кубика.
Полная схема ПЭ получается объединением трех получившихся схем в одну. Для этого внутренние обмотки трансформаторов соединяются в шести точках (кружки увеличенного диаметра, см. рис. 11).
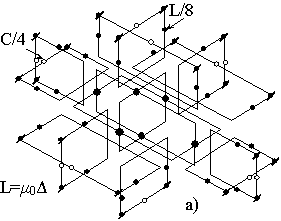
Рис. 11. Эквивалентные LC- (а) и R- (б) схемы потокового элемента.
Получившаяся эквивалентная схема потокового элемента состоит из центрального балансного трансформатора и 12 линий передач одинаковой длины, подключенных к его входам (см. рис. 12). Временные задержки в линиях, как и у роторного кубика, равны
. Волновое сопротивление линий равно волновому сопротивлению вакуума.
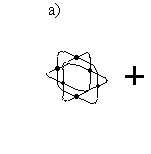
Рис. 12. Схема потокового кубика: а) центральный трансформатор, б) 6 пар линий передачи, в) полная схема.
Высокая симметрия центрального трансформатора потокового элемента обусловливает высокую симметрию и простоту его S-матрицы [16, 19, 20]:
и, соответственно, высокую скорость расчета. Выводится эта S-матрица очень просто. Если возбуждать только входы 1 и 3, то из симметрии схемы ПЭ следует, что на входах 2, 4, 5, 7, 9 и 11 никаких отраженных волн не будет. Это дает право исключить соответствующие линии передач из схемы ПЭ (см. рис. 13).


Рис. 13. Усечение схемы потокового элемента при возбуждении входов 1 и 3.
При синфазном возбуждении входов 1 и 3 не будет отраженных волн на входах 6 и 8 (см. рис. 14а), а при противофазном возбуждении – на входах 10 и 12 (см. рис. 14б).
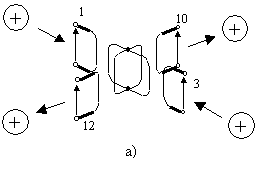
Рис. 14. Синфазное (а) и противофазное (б) возбуждение входов 1 и 3.
Складывая возбуждения, получаем картину рассеяния вида рис. 15.
Рис. 15. Рассеяние в усеченной схеме ПЭ при возбуждении входа 1.
На последнем рисунке фактически показан первый столбик S-матрицы ПЭ. Другие столбцы получаются с помощью поворотов и симметрии.
Трехмерная потоковая R
-сетка. Вычисления во временной области
Опишем алгоритм расчета во временной области для отдельно взятого потокового элемента. В момент времени
на входах элемента задается 12 падающих импульсов. В течение времени
они двигаются по направлению к трансформатору. В момент времени
производится операция “рассеяния”: каждый импульс делится на 4 части с уменьшенной вдвое амплитудой. Согласно рис. 15, рассеянные импульсы проходят вправо, влево, вверх и вниз. При этом импульсы, прошедшие вперед и отраженные назад, отсутствуют. В момент времени
мы имеем 12 отраженных импульсов на гранях ячейки. Отраженные импульсы в свою очередь являются падающими для соседних элементов, поэтому в момент времени
проводится операция “переброса” импульсов между элементами.
Данный алгоритм, как и сам потоковый элемент, был предложен в 1983 году и долгое время был самым эффективным по совокупности параметров среди алгоритмов своего класса – а именно, консервативных алгоритмов, предназначенных для моделирования нестационарных уравнений Максвелла. Под совокупностью параметров мы подразумеваем следующий набор: точность расчета, время расчета, используемый объем оперативной памяти и удобство программирования. При вычислениях по этому алгоритму используются только операции сложения, вычитания и деления пополам. Всего хранится 12 параметров на один элемент и используется 30 операций на один временной такт
. Примерно через 10-15 лет были найдены различные варианты оптимизации данного алгоритма. Оптимизированные алгоритмы позволяют хранить 6 параметров на один элемент и использовать 15 операций на один временной такт
при сохранении точности расчета [23, 24].
Граничные условия для описанного алгоритма вводятся на гранях элементов. Идеальный металл моделируется коротким замыканием клемм на грани, идеальный магнетик (магнитная стенка) – холостым ходом. Алгоритмически это соответствует изменению операции “переброса” импульсов. Например, при введении металла на грани со входами 1 и 2 соответствующие отраженные импульсы не проходят в другие кубики, а возвращаются обратно с обратным знаком. Если же на этой грани ввести магнетик, то отраженные импульсы будут возвращаться обратно без изменения знака.
При моделировании внешних задач применяются различные поглощающие граничные условия [25-27]. В простейшем случае ко входам элементов подключаются резисторы с сопротивлением, равным волновому сопротивлению вакуума. Алгоритмически это означает, отраженные импульсы полностью поглощаются нагрузкой.
Вещество моделируется также, как и для роторного кубика – подключением дополнительных двухполюсников к сетке вакуума. Самый простой вариант – подключение двухполюсников к центральному трансформатору (см. рис. 16).
Рис. 16. Модификация схемы центрального трансформатора ПЭ при моделировании диэлектрика с диэлектрической проницаемостью.
Введение шлейфов изменяет S-матрицу потокового элемента и увеличивает количество хранимых параметров до 15-18 – по общему количеству линий передач, подключенных к центральному трансформатору. В этом случае операция “переброса” импульсов между элементами не изменяется. Точно так же не изменяется и алгоритм учета граничных условий, т.е. получается, что потоковый кубик очень удобен для программирования.
Чтобы показать работу данного алгоритма, рассмотрим распространение плоской сеточной волны. Пусть плоская волна с ориентацией электрического поля “вверх” по оси X распространяется в направлении оси Z (см. рис. 17). В момент времени
на входах элементов зададим на передних гранях кубиков падающие импульсы-потоки единичной амплитуды – по одному для каждого кубика (см. рис. 17а). Направление распространения импульсов обозначим стрелками, направление электрического поля – прямоугольником. В течение времени
импульсы синхронно двигаются по направлению к трансформаторам. В момент времени
производится операция “рассеяния”: импульсы делятся на 4 части, рассеянные импульсы проходят вправо, влево, вверх и вниз. Амплитуды отраженных импульсов вдвое меньше амплитуды исходных. При этом импульсы, прошедшие вперед и отраженные назад, отсутствуют.
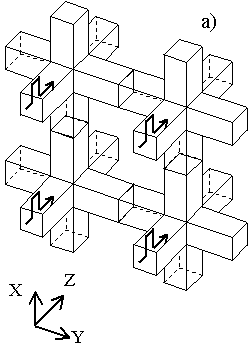
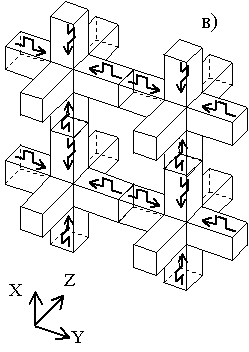
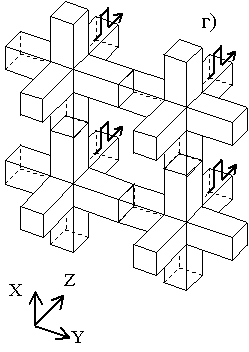
Рис. 17. Плоская сеточная волна: а) падающие импульсы-потоки на передних гранях кубиков, б) отраженные импульсы-потоки после первой операции рассеяния, в) падающие импульсы-потоки после операции “переброса”, г) отраженные импульсы-потоки после второй операции рассеяния.
После рассеяния импульсы начинают двигаются к выходам, и в момент времени
мы имеем по 4 отраженных импульса на гранях ячеек (см. рис. 17б). Отраженные импульсы в свою очередь являются падающими для соседних элементов, поэтому в момент времени
проводится операция “переброса” импульсов между элементами (см. рис. 17в). Из рис. 17б видно, что импульсы, рассеянные вправо и влево, имеют одинаковую ориентацию электрического поля. И в момент времени
эти импульсы “встретятся” с импульсами, пришедшими от соседних кубиков. Причем ориентации электрического поля этих импульсов будут такими же. Таким образом, операция “переброса” для этих импульсов будет эквивалентна операции отражения от магнитной стенки. Аналогичные рассуждения применимы и импульсам, рассеянным вверх и вниз. Только в этом случае рассеянные импульсы будут иметь противоположную ориентацию, и операция “переброса” для этих импульсов будет эквивалентна операции отражения от электрической стенки.
Проследим за дальнейшими перемещениями импульсов. После операции “переброса” импульсы двигаются по направлению к центральному трансформатору и достигают его в момент времени
. В этот момент происходит рассеяние импульсов и вместо четырех импульсов с амплитудой 1/2 появляется один импульс единичной амплитуды, который продолжает двигаться в направлении распространения волны (см. рис. 17г). Действительно, вбок ничего не отразится из-за симметрии схемы и симметричного же положения падающих импульсов. Назад ничего не отразится, потому что вклад от импульсов справа и слева полностью компенсируется вкладом от импульсов сверху и снизу. Вклады же вперед от всех импульсов складываются.
Таким образом получаем, что за два такта импульс без отражений продвинулся на один кубик вперед. Это одновременно означает два факта: во-первых, что в данном направлении отсутствует какая-либо дисперсия, и, во-вторых, что волновое сопротивление линий передач в схеме совпадает с волновым сопротивлением вакуума.
В моменты времени
, когда производится операция рассеяния, можно определить все поля в центре кубиков. Поля можно определить как до рассеяния – по падающим потокам, так и после – по отраженным. Результаты получаем идентичные:
где
,
– амплитуды импульсов-потоков, падающих на входы потоковых элементов в момент времени
;
,
– амплитуды импульсов-потоков, отраженных от входов потоковых элементов в момент времени
;
– волновое сопротивление вакуума.
В моменты времени
, когда производится операция “переброса”, можно определить поля на гранях кубиков – по 4 поля на каждой грани. Приведем формулы для определения полей на грани со входами 1 и 2:

Для возбуждения R
-сеток можно использовать классические приемы, разработанные для сеточных методов (возбуждение дельта-импульсом, функцией Хевисайда, “оконной” функцией (windowing function) и т.п. [12]). Однако наибольшее распространение получили возбуждающие схемы, называемые согласующими трансформаторами. Для R
-сеток разработано несколько типов трансформаторов: одно- и многомодовые (т.е. возбуждающие и поглощающие одну или несколько мод), одно- и многочастотные (т.е. одновременно возбуждающие и поглощающие одну или несколько частот), а также их комбинации [28].
Опишем простейшую возбуждающую схему – одночастотный одномодовый трансформатор (ООТ). Задача одномодового трансформатора – корректно возбуждать и поглощать нормальные волны основного типа. Поэтому одномодовые трансформаторы корректно работают на регулярных участках волноводов, достаточно далеко удаленных от ближайших неоднородностей. При этом необходимо, чтобы все высшие моды были запредельными. ООТ, возбуждающий в прямоугольном волноводе моду
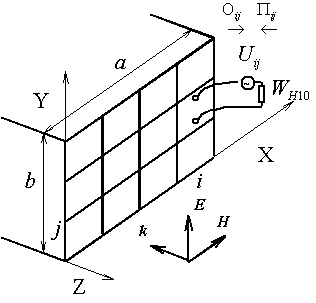
, показан на рис. 18:
Рис. 18. Одномодовый одночастотный трансформатор.
Данный трансформатор возбуждает волну с ориентацией электрического поля вдоль оси Y. В поперечном сечении волновода шириной
и высотой
, образованного из потоковых кубиков рис. 3б, к клеммам, направленным по оси Y (т.е. сонаправленным с электрическим полем) подключены генераторы потоков с внутренним сопротивлением, равным локальному характеристическому сопротивлению волны
:
,
где
– длина волны в вакууме,
– длина волны в волноводе,
– локальное характеристическое сопротивление волны
.
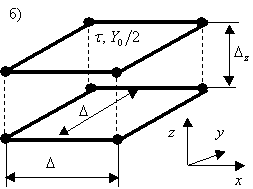
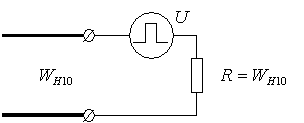
Генератор импульсов-потоков фактически является генератором импульсов напряжения, непосредственно подключенным к линии передачи с тем же внутренним сопротивлением, т.е. он возбуждает потоки в линию передачи и поглощает их без каких-либо отражений (см. рис. 19).
Рис. 19. Генератор импульсов-потоков.Возбуждение волны
эквивалентно требованию, чтобы напряжение на всех генераторах было синфазным с синусоидальным амплитудным распределением в поперечном сечении. В момент времени
генераторы начинают излучать с тактом
падающую волну, т.е. эквидистантный пакет прямоугольных импульсов с синусоидальной огибающей:
,
,
где n – номер временного такта,
– момент времени, i и j – индексы генераторов по осям X и Y соответственно,
– поток в n-й момент времени, возбуждаемый в линии, непосредственно подключенной к генератору с индексами
. Как и в обычной волне
, амплитуды генераторов
распределены по синусу вдоль оси X и постоянны вдоль оси Y:
,
,
где
– координата по оси X центра i-го кубика. Поскольку импульсы излучаются в линии передачи с характеристическим сопротивлением, отличным от характеристического сопротивления линий передачи потоковых элементов, то простая операция “переброса” для этих импульсов изменяется на операцию рассеяния на узле – 4-полюснике, представляющем собой стык двух линий передачи с разными волновыми сопротивлениями
Рис. 20. Стык двух линий передачи с разными волновыми сопротивлениями.S-матрица операции рассеяния выглядит следующим образом:
Параметры отраженной волны определяются на основе анализа Фурье импульсов, отраженных в генераторы потоков. Вычисления останавливаются при стабилизации ключевых параметров системы (S-матрицы и т.п.) в заданных пределах на протяжении заданного промежутка времени. Несмотря на нестрогость, такого критерия вполне достаточно для большинства практических задач.
Вышеописанные идеи были использованы при создании пакета “Супер-волна”, предназначенного для расчетов во временной области различных трехмерных СВЧ-устройств. С помощью данного пакета можно рассчитывать как отдельные элементы СВЧ-трактов [29], так и антенны в целом. На рис. 21 продемонстрирован расчет широкополосной плоской отражающей антенны с наклонным лучом [30], время расчета – порядка нескольких секунд.
Рис. 21. Расчет широкополосной плоской отражающей антенны с наклонным лучом.
Примеры более сложных антенн можно найти в списке литературы [31, 32]. Высокая скорость расчетов, простой интерфейс и возможность наблюдать за переходным режимом позволяет использовать пакет в учебных целях.
Сеточная дисперсия для трехмерных R
-сеток
Дискретизация пространства и времени в сеточных методах приводит при численном моделировании к возникновению пространственной анизотропии и частотной дисперсии. Дисперсионные ошибки уменьшаются при уменьшении шага дискретизации анализируемых пространственных областей. Для количественной оценки дисперсионной погрешности в методе ИАЭП введено понятие сеточной дисперсии. Данное понятие определяется для регулярной импедансной сетки. Как было указано выше, существует два основных типа сеточной дисперсии: амплитудная (зависимость характеристического сопротивления плоской сеточной волны от направления волнового вектора) и фазовая (зависимость фазовой скорости плоской сеточной волны от направления волнового вектора).
Для потоковой R
-сетки в литературе подробно исследована только фазовая дисперсия. Наиболее распространенный способ аналитического анализа дисперсных свойств потоковых R
-сеток производится в частотной области. Каждый элементарный объем рассматривается как “черный ящик”, описываемый некоторой S-матрицей [19].
В дискретном сеточном вакууме вводится декартова система координат, и каждый элемент нумеруется индексами
соответственно по оси X, Y и Z. Координаты центра ПЭ с индексами
полагаются равными
.
В непрерывном случае плоская монохроматическая волна определяется как 6-компонентная волна (по количеству компонент полей, определенных в каждой точке пространства), связь между которыми определяется из уравнений Максвелла. В дискретном сеточном вакууме, понимаемом как набор 24-полюсников, вполне естественно определить плоскую монохроматическую волну как дискретную тензорную 12-компонентную волну, связь между компонентами которой определяется S-матрицей ПЭ и топологией сетки:
где
– набор комплексных амплитуд волн, падающих на ПЭ с индексами
,
– тензорная амплитуда волны,
– радиус-вектор центра ПЭ с индексами
,
– сеточный волновой вектор,
– направление распространения волны,
– циклическая частота.
Для нахождения фазовой сеточной дисперсии требуется найти зависимость
. S-матрица ПЭ определяет связь между падающими и отраженными волнами в пределах одного элемента:
где
– набор комплексных амплитуд волн, отраженных от ПЭ с индексами
, S – S-матрица ПЭ. Топология сетки описывается уравнениями связи:
означающими, что падающие волны одновременно являются отраженными от соседних элементов. Отметим, что условие (3) справедливо для любого процесса, в т.ч. нестационарного. Ослабить данное условие нельзя, поскольку иначе мы получаем сетку с недоопределенной топологией, т.е. связями между входами элементов.
Задача (1-3) сводится к задаче на собственные значения: плоская монохроматическая волна существует тогда и только тогда, когда существуют нетривиальные решения уравнения
, где A – некоторая квадратная матрица [33]. Последнее уравнение эквивалентно условию det A = 0. Анализ определителя матрицы A приводит к выводу о том, что обе поляризации имеют одинаковую скорость, описываемую следующим дисперсионным уравнением:
где
,
– волновой вектор в непрерывном пространстве. Оценка дисперсионной погрешности формулы (4) с точностью до
дает формулу:
где
– длина волны в сетке. Максимальная погрешность реализуется при
и оценивается соотношением
. При
получим
, что соответствует ошибке по фазе 5.0° при длине исследуемого объема до
.
В работах [20, 34] выведено уравнение фазовой сеточной дисперсии для роторной сетки:
Оценка дисперсионной погрешности (6) с точностью до
дает формулу:
Сравнение формул (5) и (7) показывает, что фазовая дисперсия роторной сетки примерно в два раза выше, чем у потоковой.
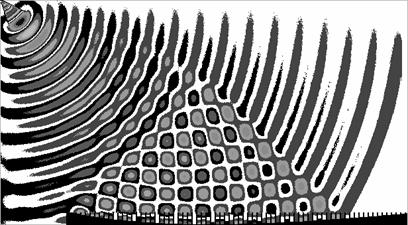
На рис. 22 и 23 представлены результаты решения дисперсионных уравнений (4) и (6) для потоковой и роторной схем соответственно. По координатным осям x, y, z отложены проекции относительной погрешности расчета волнового вектора
, выраженные в процентах, причем
.
Рис. 22. Дисперсия в потоковой сетке при
.
Рис. 23. Дисперсия в роторной сетке при
.
Анализ представленных картин приводит к следующим выводам. Длина волны
, распространяющейся в потоковой и роторной сетке, оказывается меньшей или равной длине плоской волны
, распространяющейся в свободном пространстве, т.е.
, причем
наблюдается только для потоковой сетки и только при распространении волны вдоль осей координат x, y и z.
Для потоковой сетки наибольшая погрешность при расчете волнового вектора имеет место при распространении плоской волны под углами
, а наименьшая – при распространении волны вдоль осей координат x, y и z.
Для роторной сетки получаем обратную картину: наименьшая погрешность при расчете волнового вектора имеет место при распространении плоской волны под углами
, а наибольшая – при распространении волны вдоль осей координат x, y и z.
При выборе шага сетки, удовлетворяющего условию
, относительная ошибка расчета волнового вектора
для потоковой схемы и
для роторной схемы. Таким образом, максимальная погрешность расчета волнового вектора для роторной схемы оказывается в примерно два раза большей чем для потоковой.
Другими существенными недостатками роторной R
-сетки по сравнению с потоковой является вдвое большее время анализа и более сложный для программирования вычислительный алгоритм (а именно, большое количество алгоритмических ветвей при учете границ).
Рассмотренный выше потоковый элемент – это одно из наиболее ярких достижений метода ИАЭП. Впервые потоковый элемент был открыт в Советском Союзе в 1983 году [19] – на 4 года раньше, чем на западе [35]. Причем на западе вплоть до 1999 года была неизвестна полная радиотехническая схема потокового кубика: вместо центрального трансформатора в западном варианте кубика вводится черный ящик с идентичной S-матрицей. Более того, в западной печати ведущими специалистами метода TLM неоднократно высказывалось мнение о том, что полной радиотехнической схемы потокового кубика не удастся придумать [36]. Это мнение было опровергнуто нами в 1999 году на конференции по TLM во Франции [37].
Заключение
Изложенные концепции метода ИАЭП (импедансных RLC- и R
-сеток) предполагают использование интуитивно понятной радиотехнической модели изучаемой системы и относительно простого математического аппарата, присущего теории цепей. Одной их основных задач исследователя является синтез удачной эквивалентной схемы, позволяющей создавать эффективные вычислительные алгоритмы. Достигнутые на этом пути результаты не хуже, а зачастую и превосходят результаты, достигнутые с помощью других методов.
Ввиду недостатка места, в данном обзоре не описаны двумерные RLC- и R
-сетки [20], принципы моделирования во временной области сред с частотно-зависимыми параметрами [15], метод импедансно-сеточной функции Грина [21, 22], позволяющий проводить расчеты на бесконечных сетках, и многие другие. Информацию по этим вопросам можно найти в списке литературы.
Укажем перспективные двумерные задачи метода ИАЭП:
- Разработка сеток с уменьшенной дисперсионной ошибкой.
- Моделирование процессов распространения электромагнитных волн в подмагниченной плазме.
- Создание эффективных алгоритмов для многочастотного анализа импедансных R
-сеток во временной области.
- Разработка треугольных элементов для уточнения границ.
- Разработка эквивалентных схем для киральных и бианизотронпных сред.
- Решение практических задач проектирования планарных СВЧ устройств и систем любого требуемого уровня сложности.
- Расширение метода для решения смежных физико-математических и технических задач: акустики, термодинамики, механики, гидродинамики [38].
- Уточнение схем элементов, учитывающих концентрацию поля на ребрах.
Работа выполнена при поддержке РФФИ, проект №06-01-00146.
Литература
1. Сестрорецкий Б.В. Полупроводниковые коммуникаторы для высокочастотных трактов. // В сб. “Современные проблемы антенно-волноводной техники”. –М.: Наука, 1967, стр. 126-144.
2. Сестрорецкий Б.В. Полупроводниковые регулирующие устройства СВЧ. // Раздел III монографии “СВЧ устройства на полупроводниковых диодах. Проектирование и расчет.” –М.: Сов. радио, 1969, стр. 414-572.
3. Сестрорецкий Б.В. Возможности прямого численного решения краевых задач на основе метода импедансного аналога электромагнитного пространства (ИАЭП). // Вопросы радиоэлектроники, сер. “Общетехническая”, 1976, вып. 2, стр. 113-128.
4. Иванов С.А., Сестрорецкий Б.В. Метод импедансного аналога электромагнитного пространства для двумерных задач электродинамики. // Журнал радиоэлектроники. 2007, №5, http://jre.cplire.ru/jre/may07/2/text.html.
5. Гершгорин С.А. Об электрических сетках для приближенного решения дифференциального уравнения Лапласа. // Журнал прикладной физики. 1929, т. 6, вып. 3-4, стр. 3-29.
6. Гутенмахер Л.И. Электрическое моделирование (электроинтегратор). // М.-Л.: Изд-во АН СССР, 1943, 128 стр.
7. Тетельбаум И.М. Электрическое моделирование. // М.: Физматгиз, 1959, 319 стр.
8. Федоров Н.Н. Решение некоторых задач электродинамики в неоднородных средах методами конечно разностных сеток. // Диссертация на соискание степени кандидата технических наук. –М.: МЭИ, 1969, 472 стр.
9. Kron G. Equivalent circuits of the field equations of Maxwell. // Proc. of I.R.E. May 1944. pp. 289-299.
10. Крон Г. Исследование сложных систем по частям (диакоптика). // –М.: Наука, 1972, 542 стр.
11. Johns P.B., Beurle R.L. Numerical solution of 2-dimensional scattering problems using a transmission-line matrix. // Proc. Inst. Elec. Eng. Sept. 1971, vol. 118, pp. 1203-1208.
12. Christopoulos С. The Transmission-Line Modelling (TLM) Method. Series on Electromagnetic Wave Theory. // IEEE/Oxford University Press, 1995, 232 pp.
13. Петров А.С., Иванов С.А, Королев С.А., Фастович С.В. Метод матриц линий передачи в вычислительной электродинамике. // Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 2002, №1, стр. 3-38.
14. Сестрорецкий Б.В., Владимиров Ю.К. О некоторых задачах машинного проектирования сложных СВЧ систем. // В сб. “Машинное проектирование устройств и систем СВЧ”. Общество “Знание” Украинской ССР, Киев, 1974, вып. 1, стр. 14-15.
15. Климов К.Н., Сестрорецкий Б.В., Вершков В.А., Солдатов С.В., Камышев Т.В., Рученков В.А. Электродинамический анализ двумерных неоднородных сред и плазмы. // –М. МАКС Пресс, 2005, 322 стр.
16. Кухаркин Е.С., Сестрорецкий Б.В. Диалоговая оптимизация топологии устройств в электродинамических САПР. // –М.: МЭИ, 1987, 96 стр.
17. Кустов В.Ю. Импедансная интерпретация метода конечных элементов для электродинамического анализа планарных волноводных устройств. // Диссертация на соискание степени кандидата физико-математических наук. –М.: МФТИ, 1988, 210 стр.
18. Сестрорецкий Б.В. RLC и R
-аналоги электромагнитного пространства. // Межвузовский сборник научных трудов “Машинное проектирование устройств и систем СВЧ”, МИРЭА, 1977, стр. 127-158.
19. Сестрорецкий Б.В. Балансные RLC и R
схемы элементарного объема пространства. // Вопросы радиоэлектроники, сер. “Общие вопросы радиоэлектроники”, 1983, вып. 5, стр. 56-85.
20. Сестрорецкий Б.В., Петров А.С., Иванов С.А., Климов К.Н., Королев С.А., Фастович С.В. Анализ электромагнитных процессов на основе RLC и R
сеток. // –М.: МГИЭМ, 2000, 149 стр.
21. Карцев И.Ю. Метод импедансно-сеточной функции Грина для решения двумерных задач дифракции. // Диссертация на соискание степени кандидата технических наук. –М. МЭИ, 1991, 138 стр.
22. Сестрорецкий Б.В., Карцев И.Ю. Метод импедансно-сеточной функции Грина для решения двумерных задач дифракции. // Вопросы радиоэлектроники. Сер. Общие вопросы радиоэлектроники. 1991, вып. 1, стр. 18-26.
23. P. Russer, B. Bader. The Alternating Transmission Line Matrix (ATLM) Scheme. // 1995 MTT-S International Microwave Symposium Digest, 1995, Vol. I, pp. 19-22.
24. С.А. Иванов, Б.В. Сестрорецкий, В.М. Середов, К.Н. Климов. Новые эффективные 3D алгоритмы электродинамического анализа на основе потоковых сеток. // VII Всероссийская школа-семинар “Волновые явления в неоднородных средах”, Красновидово, Московская обл., 22-27 мая, 2000 г., т. 2, стр. 101-103.
25. Berenger J.P. A perfectly matched layer for the absorption of electromagnetic waves. // J. Comput. Phys. 1994, vol. 114, pp. 185-200.
26. Berenger J.P. An Effective PML for the Absorption of Evanescent Waves in Waveguides. // IEEE Microwave and Guided Wave Letters. May 1998, vol. 8, №5, pp. 188-190.
27. Fang J. and Wu Z. Generalized perfectly matched layer for the absorption of propagating and evanescent waves in lossless and lossy media. // IEEE Trans. MTT. Dec. 1996, pp. 2216-2222.
28. Сестрорецкий Б.В., Иванов С.А., Климов К.Н. Теория и точность аппарата потоковых сеток во временной области при одночастотном и многочастотном трехмерном электродинамическом анализе. // Сб. трудов 4-й Международной научно-технической конференции “Антенно-фидерные устройства, системы и средства радиосвязи”. Воронеж, 1999, стр. 32–40.
29. B.V. Sestroretsky, M.A. Drize, S.A. Ivanov, K.N. Klimov. Tracts of Ku and C-band antennas for perspective communication satellites. // Proceedings of III International Conference on Antennas Theory and Techniques (ICATT’99). Sevastopol, Ukraine, September 8-11, 1999. Pp. 528-533.
30. Сестрорецкий Б.В., Пригода Б.А., Иванов С.А. Широкополосная плоская отражающая антенна с наклонным лучом. // Сборник трудов III международной научно-технической конференции “Антенно-фидерные устройства, системы и средства радиосвязи (ICARSM-97)”, Воронеж, Май, 1997. Т. 2. Стр. 255-263.
31. Сестрорецкий Б.В., Пригода Б.А., Дризе М.А., Иванов С.А. Электродинамическое исследование однослойной антенны с круговой поляризацией Ка диапазона с отверстиями сложной конфигурации. // IХ Международная Крымская Микроволновая конференция “СВЧ техника и телекоммуникационные технологии”, Севастополь, Украина, 13-16 сентября, 1999. Стр. 196-198.
32. B.V. Sestroretsky , A.V. Dorofeev, A.N. Savchenko, M.A. Drize, S.A. Ivanov. Electrodynamic modelling of two-port C-band flat antenna. // Proceedings of III International Conference on Antenna Theory and Techniques (ICATT-99). Sevastopol, Crimea, Ukraine, September 8-11, 1999. Pp. 350-352.
33. S.A. Ivanov, B.V. Sestroretsky. Dispersion of plane waves in 3D stream type grids. // Proceedings of 1998 International Conference on Mathematical Methods in Electromagnetic Theory (MMET'98). Kharkov, Ukraine, June 2-5, 1998. Vol. 2. Pp. 600-602.
34. Nielsen J. S and Hoefer W. J. R. Generalized dispersion analysis and spurious modes of 2-D and 3-D TLM formulations. // IEEE Trans. Microwave Theory Tech., 1993, Aug., pp. 1375-1384.
35. Johns P.B. A Symmetrical Condensed Node for the TLM Method. // IEEE Transactions on Microwave Theory and Techniques. Apr. 1987, pp. 370-377.
36. Trenkič V. The development and characterization of advanced nodes for the TLM method. // Thesis philosophy doctor degree. University Nottingham. –1995.
37. B.V. Sestoretsky, S.A. Ivanov. A new 6-parametrical three-dimensional algorithm for 12-port symmetrical condensed node. // Third International Workshop on Transmission Line Matrix (TLM) Modelling Theory and Applications, University of Nice-Sophia Antipolis, France, Oct., 27–29, 1999, pp 197-200.
38. Digest of the Third international workshop on transmission line matrix (TLM). // University of Nice-Sophia Antipolis, France, October 27–29, 1999, 325 рр.



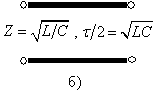











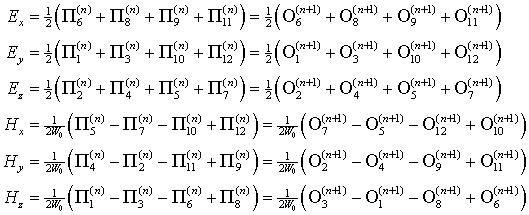
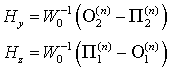


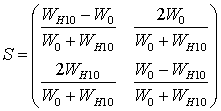


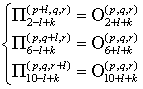 ,
,
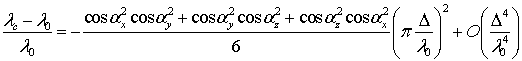 (5)
(5)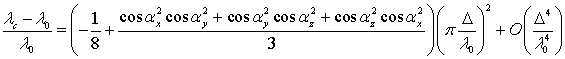 (7)
(7)
