УДК 539.3: 537.633.9
Пироэлектрические свойства ПОРИСТОГО ТИТАНАТА БАРИЯ
А.
А. Паньков
Пермский национальный исследовательский политехнический университет
Статья получена 27 октября 2014 г.
Аннотация. Получено новое решение связанной краевой задачи электромагнитоупругости в обобщенном сингулярном приближении статистической механики композитов на основе новых решений для сингулярных составляющих вторых производных функций Грина для однородной трансверсально-изотропной пьезоэлектромагнитной среды с эллипсоидальным зерном неоднородности. Представлены результаты расчета эффективных температурных коэффициентов и пироэлектрической постоянной пористого титаната бария для различных значений степени пористости и формы: пластинчатых, сферических, игольчатых и туннельных пор.
Ключевые слова: пьезокомпозит, краевая задача электромагнитоупругости, эффективные пироэлектрические свойства.
Abstract. New decision of stochastic connected boundary-volume problem of electro-magnetic elasticity by generalized singular approach of statistical mechanical of composites is received on base of the new decisions for singular parts of second derived Green’s function for uniform transversal-isotropic piezo electro-magnetic media. Results of calculation of effective temperature factors and a pyroelectric constant of porous barium titanate for various values of porosity and for some porosity forms are presented.
Key words: piezocomposite, boundary value problem of electro-magnetic elasticity, effective pyroelectric properties.
Введение
Пироэлектрический эффект состоит в генерации электрических зарядов в кристалле под действием теплового инфракрасного излучения. Изменение спонтанной поляризации и появление электрического поля в пироэлектриках может происходить не только при изменении температуры, но и при механической деформации. Пироэлектрический эффект используется для обнаружения инфракрасного излучения при изменении температуры с точностью до 10-6 К. Пироэлектрические приемники имеют малую инерционность, постоянная времени составляет 10-5 ‑ 10-7 с и менее. Пироэлектрические материалы находят широкое применение в качестве сенсорных устройств различного назначения, детекторов и приемников излучений, датчиков теплометрических приборов, для индикации пространственного распределения излучений в системах визуализации ИК-изображений в темновидении. Разработка новых пироэлектрических материалов и создание устройств на их основе ‑ активно развивающееся направление сегнетоэлектрического материаловедения [1‑3]. В композиционных материалах пироэлектрический эффект может по отдельности отсутствовать в каждом компоненте и возникновение такого эффекта на макроуровне композита связано с взаимодействием элементов структуры на микроуровне [4, 5].
Цель работы – исследование закономерностей влияния структурных параметров композита на его эффективные пироэлектромагнитные свойства на основе решения связанной краевой задачи термоэлектромагнитоупругости статистической механики композитов [6–8] с использованием новых решений [8‑10] для сингулярных составляющих вторых производных функций Грина для однородной трансверсально-изотропной пьезоэлектромагнитной среды с эллипсоидальным зерном неоднородности.
2. Микро- и макроуровни
Рассматриваем двухфазные
пьезоактивные среды в представительной области ![]() ,
определяющие соотношения для фаз
,
определяющие соотношения для фаз ![]() [5,
7, 8]
[5,
7, 8]
![]() ,
,
![]() ,
(1)
,
(1)
![]() ,
,
связывают напряжения ![]() , индукции электрического
, индукции электрического
![]() и магнитного
и магнитного ![]() полей
с деформациями
полей
с деформациями ![]() , напряженностями электрического
, напряженностями электрического
![]() и магнитного
и магнитного ![]() полей,
температурой однородного внешнего нагрева
полей,
температурой однородного внешнего нагрева ![]() через
считающиеся известными для каждой фазы
через
считающиеся известными для каждой фазы ![]() тензоры
упругих свойств
тензоры
упругих свойств ![]() , пьезоэлектрических
, пьезоэлектрических ![]() и пьезомагнитных
и пьезомагнитных ![]() свойств,
диэлектрических
свойств,
диэлектрических ![]() и магнитных
и магнитных ![]() проницаемостей, температурных
коэффициентов
проницаемостей, температурных
коэффициентов ![]() , пироэлектрических постоянных
, пироэлектрических постоянных ![]() и
и ![]() .
Выполняются условия идеального контакта на межфазных поверхностях: непрерывность
векторов перемещений, напряжений, индукций электрического и магнитного полей.
Тензоры эффективных свойств
.
Выполняются условия идеального контакта на межфазных поверхностях: непрерывность
векторов перемещений, напряжений, индукций электрического и магнитного полей.
Тензоры эффективных свойств ![]() , …,
, …, ![]() входят в определяющие соотношения на
макроуровне композита
входят в определяющие соотношения на
макроуровне композита
![]() ,
,
![]()
и связывают осредненные или
макроскопические значения напряжений ![]() , деформаций
, деформаций ![]() , индукций
, индукций ![]() ,
, ![]() , напряженностей
, напряженностей ![]() ,
,
![]() электрического и магнитного полей
соответственно;
электрического и магнитного полей
соответственно; ![]() ‑ оператор осреднения по
области
‑ оператор осреднения по
области ![]() структурных полей.
структурных полей.
3. Обобщенное сингулярное приближение
Решение
для тензора эффективных температурных напряжений ![]() и
векторов эффективных пироэлектрических
и
векторов эффективных пироэлектрических ![]() и
пиромагнитных
и
пиромагнитных ![]() постоянных композита в
обобщенном сингулярном приближении получено в виде
постоянных композита в
обобщенном сингулярном приближении получено в виде
![]() ,
,
![]() ,
(3)
,
(3)
![]()
через поправки к соответствующим
осредненным по области ![]() значениям:
значениям: ![]() ,
, ![]() ,
, ![]() , тензоры разностей:
, тензоры разностей: ![]() ,
, ![]() ,…,
,…, ![]() ;
; ![]() ‑
относительное объемное содержание 1-й фазы в
‑
относительное объемное содержание 1-й фазы в ![]() .
Вошедшие в (3) компоненты тензоров
.
Вошедшие в (3) компоненты тензоров ![]() ,
, ![]() и
и ![]() находим
из решения системы алгебраических уравнений
находим
из решения системы алгебраических уравнений
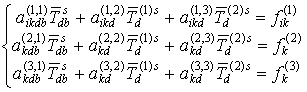 (4)
(4)
где коэффициенты
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() , (5)
, (5)
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
и правые части
![]() ,
(6)
,
(6)
![]() ;
;
индексы в круглых скобках ![]() обозначают выделение симметричной
составляющей по этой паре индексов, тензоры разностей:
обозначают выделение симметричной
составляющей по этой паре индексов, тензоры разностей:
В формулы (5), (6) входит новое
решение для матрицы тензоров сингулярных
составляющих ![]() вторых производных функций Грина
вторых производных функций Грина ![]()
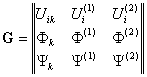 ,
,
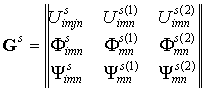
для однородной анизотропной пьезоэлектромагнитной
«среды сравнения» [6], свойства которой заданы через тензоры: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (7), функция Грина
(7), функция Грина ![]() ,
, ![]() ‑
дельта-функция Дирака,
‑
дельта-функция Дирака, ![]() , в точке
, в точке ![]() действует единичная объемная сила, или
электрический или магнитный источник,
действует единичная объемная сила, или
электрический или магнитный источник, ![]() ‑
оператор дифференцирования по координатам вектора
‑
оператор дифференцирования по координатам вектора ![]() .
Компоненты матрицы
.
Компоненты матрицы ![]() в (8) вычисляются по формулам
в (8) вычисляются по формулам
![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
,
![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
,
где оператор
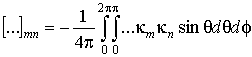
действует на компоненты тензоров
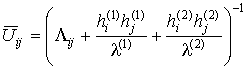 ,
,
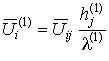 ,
,
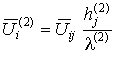 ,
,
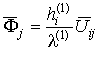 ,
,
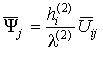 ,
,
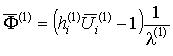 ,
,
 ,
,
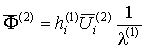 ,
,
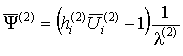 ,
,
в которых использованы обозначения
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
(9)
,
(9)
 ,
,
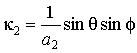 ,
,
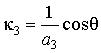 ,
,
![]() и
и ![]() ‑ полярные углы в сферической
системе координат, поверхность эллипсоидального «зерна неоднородности» [6]
задана равенством
‑ полярные углы в сферической
системе координат, поверхность эллипсоидального «зерна неоднородности» [6]
задана равенством
через значения главных полуосей ![]() в (9),
в (9), ![]() –
координаты вектора
–
координаты вектора ![]() .
.
4. Численный расчет
Проведем расчет отличных от нуля
эффективных температурных коэффициентов ![]() ,
, ![]() и пироэлектрической постоянной
и пироэлектрической постоянной ![]() титаната бария с распределенными по
объему керамики ориентированными эллипсоидальными порами при различных степенях
наполнения
титаната бария с распределенными по
объему керамики ориентированными эллипсоидальными порами при различных степенях
наполнения ![]() . Главные полуоси
. Главные полуоси ![]() эллипсоидальных
пор ориентированы вдоль соответствующих координатных осей
эллипсоидальных
пор ориентированы вдоль соответствующих координатных осей ![]() (9), (10). Свойства среды сравнения в
(7), (9) приравниваем к осредненным по объему значениям:
(9), (10). Свойства среды сравнения в
(7), (9) приравниваем к осредненным по объему значениям: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Независимые упругие, диэлектрические и
пьезомеханические постоянные трансверсально-изотропных электроупругих свойств
титаната бария [5]:
. Независимые упругие, диэлектрические и
пьезомеханические постоянные трансверсально-изотропных электроупругих свойств
титаната бария [5]:
![]() Па,
Па, ![]() ,
, ![]() Па,
Па,
![]() Па,
Па, ![]() Па,
Па,
![]() Кл/м2,
Кл/м2, ![]() Кл/м2,
Кл/м2, ![]() Кл/м2,
Кл/м2,
![]() Ф/м,
Ф/м, ![]() Ф/м,
Ф/м,
![]() Па/К,
Па/К, ![]() Па/К,
Па/К,
![]() Кл/Км2
Кл/Км2
Дополнительные ненулевые компоненты тензоров ![]() ,
, ![]() и
и ![]() могут быть выражены через значения
независимых компонент по формулам
могут быть выражены через значения
независимых компонент по формулам
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
с учетом симметрии: ![]() ,
, ![]() .
.
|
|
|
|
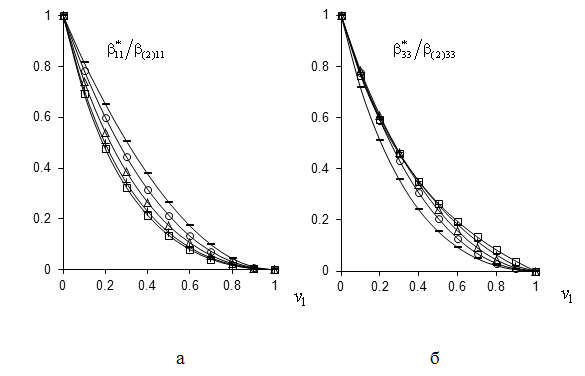
Рис. 1. Эффективные температурные
коэффициенты |
|
|
|
Рис. 2 Эффективный объемный
пьезомодуль
|
Результаты расчета эффективных
температурных коэффициентов ![]() ,
, ![]() , пироэлектрической постоянной
, пироэлектрической постоянной ![]() и, дополнительно, объемного пьезомодуля
и, дополнительно, объемного пьезомодуля ![]() , пористого титаната бария приведены на
рис. 1 и рис. 2 для различных значений степени наполнения
, пористого титаната бария приведены на
рис. 1 и рис. 2 для различных значений степени наполнения ![]() . при варьировании параметром формы
. при варьировании параметром формы ![]() : 0,5 (-), 1 (
: 0,5 (-), 1 (![]() ), 2 (
), 2 (![]() ), 5 (+),
), 5 (+), ![]() (
(![]() )
эллипсоидальных пор. Отметим, что компоненты
)
эллипсоидальных пор. Отметим, что компоненты ![]() ,
, ![]() рассчитываются
рассчитываются ![]() через
компоненты тензоров эффективных пьезоэлектрических модулей
через
компоненты тензоров эффективных пьезоэлектрических модулей ![]() и упругих свойств
и упругих свойств ![]() (2)
[8].
(2)
[8].
Заключение
Получено новое решение для тензоров эффективных пироэлектромагнитных свойств композитов, фазы которых, в общем случае, обладают пьезо- и пироэффектом как в электрических, так и в магнитных полях. Решение получено в рамках известного и хорошо апробированного подхода статистической механики композитов [6–8] на основе решения связанной краевой задачи электромагнитоупругости статистической механики композитов с использованием новых решений для сингулярных составляющих вторых производных функций Грина для однородной трансверсально-изотропной пьезоэлектромагнитной среды с эллипсоидальным зерном неоднородности. Проведен анализ влияния формы и величины относительного объемного содержания ориентированных эллипсоидальных (дисковых, шаровых, игольчатых, туннельных) пор на эффективные температурные коэффициенты, пироэлектрическую постоянную и объемный пьезомодуль пористого титаната бария.
Работа выполнена при финансовой поддержке гранта РФФИ № 14-01-96004 р_урал_а.
Литература
1. Коротких Н.И., Матвеев Н.Н., Сидоркин А.С. Пироэлектрические свойства полиэтиленоксида // Физика твердого тела, 2009, Т.51, №6.‑С.1215‑1217.
2. Смирнова Е.П., Александров С.Е., Сотников К.А., Капралов А.А., Сотников А.В. Пироэлектрический эффект в твердых растворах на основе магнониобата свинца // Физика твердого тела, 2003, Т.45, №7.‑С.1245‑1249.
3. Ярмаркин В.К., Шульман С.Г., Панкова Г.А., Леманов В.В. Пироэлектрические свойства кристаллов некоторых соединений на основе белковых аминокислот// Физика твердого тела, 2005, Т.47, №1.‑С.2047‑2049.
4. Керимов М.К., Курбанов М.А., Агаев Ф.Г., Мусаева С.Н., Керимов Э.А. Пироэлектрический эффект в композитах, кристаллизованных в условиях действия плазмы электрического разряда // Физика твердого тела, 2005, Т.47, №4.‑С.686‑690.
5. Каралюнас Р.И. Эффективные термопьезоэлектрические свойства слоистых композитов // Механика композит. материалов, 1990, № 5.–С.823–830.
6. Шеpмеpгоp Т.Д. Теоpия упpугости микpонеодноpодных сpед. ‑ М.: Наука, 1976.‑399с.
7. Хорошун Л.П., Маслов Б.П., Лещенко П.В. Прогнозирование эффективных свойств пьезоактивных композитных материалов. – Киев: Наук. думка, 1989. –208с.
8. Паньков А.А. Статистическая механика пьезокомпозитов. ‑ Пермь: Изд-во Перм. гос. техн. ун-та, 2009. –480с.
9. Паньков А.А. Максвелл-вагнеровская релаксация в пьезокомпозите PVF/феррит с эллипсоидальными включениями в переменном электрическом поле // Журнал радиоэлектроники: электронный журнал. 2013. ‑ №6 . URL: http://jre.cplire.ru/jre/jun13/12/text.pdf
10. Паньков А.А. Влияние разупорядоченности и инверсии фаз на электромагнитную связанность пьезокомпозита с квазипериодической структурой // Журнал радиоэлектроники: электронный журнал. 2014. ‑ №1. URL: http://jre.cplire.ru/jre/jan14/12/text.pdf