УДК 537.874; 537.624
СТОХАСТИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ ТРАЕКТОРИЙ ПОВЕРХНОСТНЫХ МАГНИТОСТАТИЧЕСКИХ ВОЛН В ПОЛЕ ТИПА «ВАЛА» С ПРОСТРАНСТВЕННОЙ МОДУЛЯЦИЕЙ
В. И. Щеглов
Институт радиотехники и электроники им. В.А.Котельникова
РАН
Статья получена 23 сентября 2014 г.
Аннотация. Рассмотрено распространение поверхностных магнитостатических волн (ПМСВ) в ферритовой пластине, намагниченной неоднородным полем типа «вала» с пространственной модуляций. Показано, что в этих условиях траектории волновых пучков ПМСВ приобретают стохастический характер, проявляющийся в хаотических скачках амплитуды, частоты и фазы. Выявлен эффект “высвечивания” траекторий, состоящий в их обрыве при выходе в область пространства, где поле становится меньше соответствующего нижней границе спектра ПМСВ. Показано, что наиболее сильную хаотизацию траекторий вызывает модуляция крутизны склонов «вала», несколько меньшую модуляция высоты вершины и самую меньшую – модуляция сдвига его вершины. Выявлено, что наиболее сильная стохастизация происходит при работе на частоте, близкой к верхней границе спектра ПМСВ. Отмечена аналогия наблюдаемых явлений с движением частицы в «перемешивающем биллиарде». В качестве параметра, обеспечивающего «перемешивание», указано волновое число ПМСВ. Рассмотрена практическая реализация наблюдаемых явлений и даны рекомендации к их наблюдению в эксперименте.
Ключевые слова: феррит, магнитостатическая волна, стохастические колебания.
Abstract. The propagation of magnetostatic surface waves (MSSW) in ferrite plate biased by nonuniform magnetic “bank-type” field with space modulation is investigated. It is shown that in this conditions the MSSW wave beam paths take place of chaotic character showed in chaotic jumps of amplitude, frequency and phase. In is found the effect of path “outshining”, consist of its breaking by outgoing to the same space region where the field is less than low field boundary of MSSW spectrum. It is shown that the most strong paths chaotic character is caused by modulation of slope ”bank” steepness, slightly less of top height and the least – the displacement of its top. It is shown that the most strong chaotic character take place by the work on the frequency near the top boundary of MSSW spectrum. It was noted that observed phenomena are resembled to the particle motion in “mixing billiard”. In the parameter which makes mixing it was shown to wave number of MSSW. It was considered the practice realization of observed phenomena and made the recommendations to its experiment observation.
Key words: ferrite, magnetostatic wave, chaotic vibrations.
Введение
В физике непрерывно растет интерес к процессам, проявляющим стохастические свойства [1,2]. Значительное внимание привлекают хаотические колебания полностью детерминированной системы, возникающие при также детерминированном периодическом воздействии, в первую очередь – стохастический резонанс [2]. Наряду с общими вопросами, значительное внимание уделяется неустойчивостям стохастического характера в магнитных средах, в первую очередь в ферритах. Подробно исследованы условия нелинейного ферромагнитного резонанса, где при превышении порогового уровня возбуждения наблюдается параметрическое возбуждение обменных спиновых волн, сопровождаемое хаотическим изменением их амплитуды автомодуляционного характера [3,4]. В работах [5-7] выявлены дополнительные условия возбуждения такой неустойчивости, в частности показано, что в геометрии нормально намагниченной тонкой пластины параметрические явления подавляются, что позволяет достичь углов прецессии вектора намагниченности до сорока и более градусов. В работе [8] описаны возникающие при таких углах весьма разнообразные виды неустойчивостей в том числе бифуркационного характера.
Все неустойчивости, описанные в перечисленных работах [3-8] относятся к развитию процессов во времени. С другой стороны, в ряде работ [9-11], где рассматривалось пространственное распространение волновых пучков поверхностных магнитостатических волн (ПМСВ) в касательно намагниченных пленках ферритов, было показано, что при намагничивании пленки полем типа «вала» траектории волновых пучков ПМСВ имеют «псевдосинусоидальный» колебательный характер, в котором роль времени играет координата, параллельная оси «вала».
В работе [12] было впервые показано, что при периодическом воздействии на такую пространственно детерминированную систему сигналом, в пространстве также полностью детерминированным, например, при модуляции параметров «вала» по синусоидальному закону, система проявляет стохастические свойства: ее пространственные колебания приобретают хаотический характер.
Несколько более подробно этот эффект рассматривался в работе [13]. В работах [14,15] были рассмотрены особенности хаотизации траекторий ПМСВ при различных видах модуляции поля «вала», а в работе [16] установлен их фрактальный характер. В работе [17] отмечена возможность хаотизации траекторий ПМСВ для обратных волн, распространяющихся в пленке, намагниченной поперечно неоднородным модулированным полем типа «вала». В работе [18] рассмотрена возможность хаотизации траекторий ПМСВ в условиях распространения в системе нескольких параллельных каналов, образованной полями типа промодулированного «вала». В работе [19] обобщены полученные ранее результаты с единой точки зрения.
Настоящая работа посвящена дальнейшему развитию результатов, полученных в работах [12-19], с целью выявления наиболее общих закономерностей явления стохастической неустойчивости траекторий ПМСВ в модулированном поле типа «вала».
1. Геометрия задачи и основные уравнения
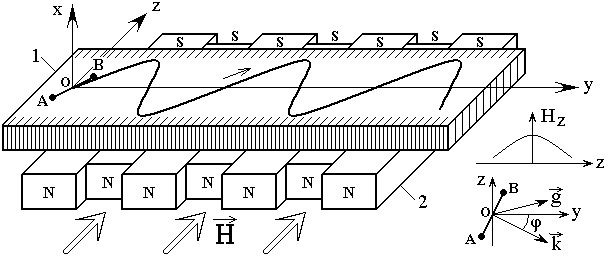
Геометрия задачи, совпадающая с принятой в [19], показана на рис.1.
Рис.1. Геометрия задачи.
Ферритовая пластина 1
намагничена постоянным полем ![]() в ее плоскости. Конфигурация
этого поля соответствует профилю типа «вала». Магнитная система 2 формирует
дополнительное поле, реализующее пространственную модуляцию исходного поля. Преобразователь
АВ возбуждает ПМСВ в плоскости пластины. Декартова система координат
в ее плоскости. Конфигурация
этого поля соответствует профилю типа «вала». Магнитная система 2 формирует
дополнительное поле, реализующее пространственную модуляцию исходного поля. Преобразователь
АВ возбуждает ПМСВ в плоскости пластины. Декартова система координат ![]() ориентирована таким образом, что
плоскость
ориентирована таким образом, что
плоскость ![]() совпадает с плоскостью магнитной
пластины, а ось
совпадает с плоскостью магнитной
пластины, а ось ![]() ей перпендикулярна. При этом
ось
ей перпендикулярна. При этом
ось ![]() ориентирована вдоль направления постоянного
поля. Начало координат О совпадает с центром преобразователя АВ. На врезках
справа внизу показана схема конфигурации поля типа «вала», а также ориентация
векторов фазовой
ориентирована вдоль направления постоянного
поля. Начало координат О совпадает с центром преобразователя АВ. На врезках
справа внизу показана схема конфигурации поля типа «вала», а также ориентация
векторов фазовой ![]() и групповой
и групповой ![]() скоростей ПМСВ в полярной системе
координат.
скоростей ПМСВ в полярной системе
координат.
В приведенных условиях поле ![]() формирует в пластине волноведущий канал,
параллельный оси
формирует в пластине волноведущий канал,
параллельный оси ![]() . В отсутствие модуляции ПМСВ
распространяется в этом канале по периодической волнообразной траектории,
напоминающей синусоиду, и называемой далее «псевдосинусоидальной» (на рисунке
показана утолщенной линией). Модуляция поля, осуществляемая системой 2,
приводит к искажению исходной «синусоиды», в результате чего траектория
приобретает стохастический характер.
. В отсутствие модуляции ПМСВ
распространяется в этом канале по периодической волнообразной траектории,
напоминающей синусоиду, и называемой далее «псевдосинусоидальной» (на рисунке
показана утолщенной линией). Модуляция поля, осуществляемая системой 2,
приводит к искажению исходной «синусоиды», в результате чего траектория
приобретает стохастический характер.
При распространении ПМСВ в
неоднородно намагниченной пластине величина и направление ее волнового вектора ![]() изменяется. Для локальной характеристики
свойств волны в заданной точке пространства
изменяется. Для локальной характеристики
свойств волны в заданной точке пространства ![]() удобно
пользоваться полярной системой координат (рис.1, вставка), где компоненты
волнового вектора ПМСВ равны:
удобно
пользоваться полярной системой координат (рис.1, вставка), где компоненты
волнового вектора ПМСВ равны:
![]() ;
(1)
;
(1)
![]() .
(2)
.
(2)
В геометрии рис.1 дисперсионное соотношение для ПМСВ имеет вид [9-11, 20]:
где:
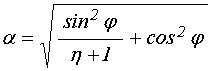 ;
(4)
;
(4)
![]() ;
(5)
;
(5)
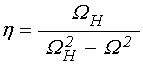 ;
(6)
;
(6)
 ;
(7)
;
(7)
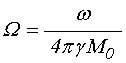 ;
(8)
;
(8)
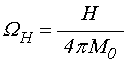 ,
(9)
,
(9)
где ![]() –
толщина магнитной пластины,
–
толщина магнитной пластины, ![]() – намагниченность насыщения,
– намагниченность насыщения,
![]() – гиромагнитная постоянная,
– гиромагнитная постоянная, ![]() – частота.
– частота.
Для задач о распространении волновых пучков ПМСВ в неоднородных полях удобно пользоваться методом Гамильтона-Аулда, состоящим в решении системы уравнений [9-11,21-22]:
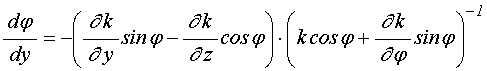 ;
(11)
;
(11)
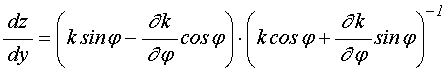 ,
(12)
,
(12)
где функция ![]() определяется
дисперсионным соотношением (3) при заданной частоте
определяется
дисперсионным соотношением (3) при заданной частоте ![]() и
значении поля
и
значении поля ![]() по ходу распространения волны.
Получаемая при пошаговом решении системы (10)-(12) зависимость
по ходу распространения волны.
Получаемая при пошаговом решении системы (10)-(12) зависимость ![]() от
от ![]() дает
траекторию распространения ПМСВ при заданной конфигурации поля.
дает
траекторию распространения ПМСВ при заданной конфигурации поля.
В настоящей работе система (10)-(12) решалась численно методом Рунге-Кутта четвертого порядка [23], результаты чего описаны далее.
2. Модуляция поля типа «вала»
Будем полагать, что поле, в
основном, направлено вдоль оси ![]() , то есть его z-компонента значительно преобладает
над другими компонентами (x
и y), так что влиянием этих компонент
на траектории ПМСВ можно пренебречь. Назовем полем типа «вала» такое поле, z-компонента которого имеет вид:
, то есть его z-компонента значительно преобладает
над другими компонентами (x
и y), так что влиянием этих компонент
на траектории ПМСВ можно пренебречь. Назовем полем типа «вала» такое поле, z-компонента которого имеет вид:
где: ![]() ,
, ![]() ,
, ![]() –
параметры «вала», из которых первый характеризует его высоту, второй – крутизну
склонов и третий – сдвиг вершины вдоль оси
–
параметры «вала», из которых первый характеризует его высоту, второй – крутизну
склонов и третий – сдвиг вершины вдоль оси ![]() ,
причем предполагается, что
,
причем предполагается, что ![]() . Отсутствие модуляции
поля соответствует постоянству всех этих параметров. При этом траектории ПМСВ
имеют чисто периодический «псевдосинусоидальный» вид [9-11].
. Отсутствие модуляции
поля соответствует постоянству всех этих параметров. При этом траектории ПМСВ
имеют чисто периодический «псевдосинусоидальный» вид [9-11].
Положим, что модуляция поля осуществляется путем изменения одного из упомянутых параметров по синусоидальному закону следующего вида:
где ![]() . При
этом:
. При
этом: ![]() – постоянная и
– постоянная и ![]() –
переменная части параметра,
–
переменная части параметра, ![]() – амплитуда и
– амплитуда и ![]() – частота пространственной модуляции
поля. Для характеристики такого поля введем параметр глубины модуляции:
– частота пространственной модуляции
поля. Для характеристики такого поля введем параметр глубины модуляции:
Глубина модуляции может
меняться от 0 до 1. При ![]() модуляция отсутствует,
при
модуляция отсутствует,
при ![]() величина
величина ![]() при изменении
при изменении
![]() меняется от нуля до
меняется от нуля до ![]() .
.
3. Общая картина неустойчивости траекторий ПМСВ
ПМСВ, распространяющиеся в таком модулированном поле, периодически испытывают воздействия, приходящееся на разные участки траекторий. По мере распространения ПМСВ вдоль канала, образуемого полем типа «вала», такие воздействия накапливаются, а поскольку они приходится на разные участки траектории, то вид ее резко изменяется – от периодического псевдосинусоидального до близкого к хаотическому. Траектория становится неустойчивой в том отношении, что малое изменение начальных условий приводит к сильному изменению ее формы. Численный расчет показывает, что траектория испытывает достаточно сильные (более 10% от невозмущенной величины) хаотические скачки амплитуды, частоты и фазы при глубине модуляции более 0,2-0,4. Явления стохастизации проявляются тем сильнее, чем больше глубина модуляции. Если в процессе какого-либо из скачков превышается угол отсечки, то траектория обрывается. Далее будем называть такой обрыв «высвечиванием».
4. Основные свойства хаотизации траекторий
Рассмотрим некоторые общие свойства хаотизации траекторий ПМСВ на примере поля типа «вала» с модулированной крутизной склонов [12,13] вида:
Положим здесь и далее основные
параметры задачи следующими: параметры пленки ![]() ,
, ![]() ,
частота ПМСВ
,
частота ПМСВ ![]() , начало траектории соответствует
, начало траектории соответствует
![]() ,
, ![]() . Начальный угол
. Начальный угол ![]() между волновым вектором
между волновым вектором ![]() и осью
и осью ![]() кроме особо оговоренных случаев
будем считать равным
кроме особо оговоренных случаев
будем считать равным ![]() .
.
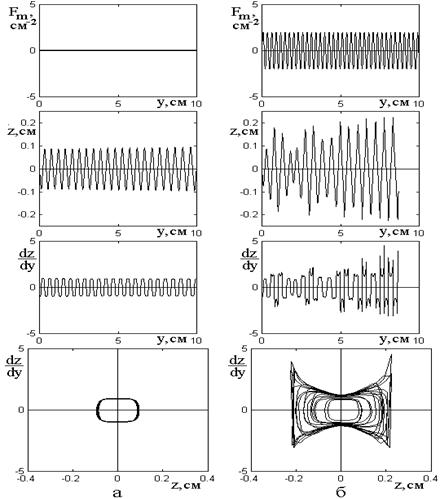
Рис.2. Хаотизация траекторий ПМСВ в поле типа «вала» с модулированной крутизной склонов.
а – модуляция отсутствует; б – модуляция присутствует.
Параметры поля: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Результаты иллюстрируются рис.2, где
левый столбец (а) соответствует немодулированному полю, а правый (б) –
модулированному. Первая пара рисунков соответствует зависимости от координаты
![]() параметра
параметра ![]() , характеризующего крутизну склонов «вала». В отсутствие
модуляции (
, характеризующего крутизну склонов «вала». В отсутствие
модуляции (![]() ) он просто равен нулю, при наличии модуляции (
) он просто равен нулю, при наличии модуляции (![]() ) имеет вид синусоиды. На второй
паре рисунков показаны траектории ПМСВ
) имеет вид синусоиды. На второй
паре рисунков показаны траектории ПМСВ ![]() для тех же случаев. На третьей
паре – производные от траекторий по координате
для тех же случаев. На третьей
паре – производные от траекторий по координате ![]() –
– ![]() , и на четвертой – фазовые портреты
колебаний (зависимости
, и на четвертой – фазовые портреты
колебаний (зависимости ![]() от
от ![]() ) в тех же условиях. Из сопоставления рисунков каждой
пары видно, что в отсутствие модуляции (а) траектория ПМСВ и ее производная
имеют строго периодический близкий к синусоидальному характер, а фазовая
траектория описывает один и тот же цикл. При наличии модуляции (б) амплитуда
траектории ПМСВ и ее производной испытывают хаотические скачки, а фазовая
траектория каждый новый оборот совершает по иному и фазовый портрет
размазывается, что соответствует стохастизации процесса.
) в тех же условиях. Из сопоставления рисунков каждой
пары видно, что в отсутствие модуляции (а) траектория ПМСВ и ее производная
имеют строго периодический близкий к синусоидальному характер, а фазовая
траектория описывает один и тот же цикл. При наличии модуляции (б) амплитуда
траектории ПМСВ и ее производной испытывают хаотические скачки, а фазовая
траектория каждый новый оборот совершает по иному и фазовый портрет
размазывается, что соответствует стохастизации процесса.
5. Структура траекторий
Как можно видеть из рис.2, траектории ПМСВ и особенно их производные часто имеют скачкообразный характер, который повторяется и на фазовых портретах. Поскольку распространение ПМСВ по плоскости пленки является непрерывным, представляет интерес рассмотреть, в какой мере эта скачкообразность имеет место. Для этого обратимся к рис.3, где показаны траектории ПМСВ, их производные и фазовые портреты. Левый столбец рисунков соответствует масштабу, близкому к принятому на рис.2, правый – те же траектории, снятые в более крупном масштабе (крупнее на два порядка). Буквами А и В обозначены идентичные места обеих видов траекторий.
Из рисунка видно, что во всех случаях скачкообразный характер траекторий на самом деле таковым не является, то есть все кривые в достаточно крупном масштабе являются совершенно плавными, как этого и следовало ожидать исходя из физической сущности процесса.

Рис.3. Структура траекторий (1) и фазовых портретов (2) в крупном масштабе.
а – траектории ПМСВ;
б – производные от траекторий;
в – фазовые портреты (показана часть одной фазовой траектории).
Параметры поля: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Частота
модуляции:
. Частота
модуляции: ![]() .
.
Остальные параметры совпадают с принятыми на рис.2.
6. Изменение начальных условий
Зависимость формы траектории от
малого изменения начальных условий весьма высока. Так, при изменении начального
угла ![]() на
на ![]() с
с ![]() до
до ![]() в отсутствие
модуляции траектория сдвигается на четверть периода после 22-25 пересечений оси
в отсутствие
модуляции траектория сдвигается на четверть периода после 22-25 пересечений оси
![]() . При наличии модуляции аналогичное изменение траектории
происходит уже при 5-6 пересечениях.
. При наличии модуляции аналогичное изменение траектории
происходит уже при 5-6 пересечениях.
Рассмотрим, как сказывается на
характере стохастизации траекторий ПМСВ изменение начальных условий, в качестве
примера которых возьмем изменение начального угла вектора фазовой скорости
волны. Для этого обратимся к рис.4, где показаны траектории ПМСВ (а), их производные
(б) и фазовые портреты (в) при различных значениях начального угла ![]() . Как более наглядный рассмотрен случай
модуляции высоты вершины «вала».
. Как более наглядный рассмотрен случай
модуляции высоты вершины «вала».
При разных углах амплитуды
смещения траектории по оси ![]() и его производной в
отсутствие модуляции составляют:
и его производной в
отсутствие модуляции составляют:
при ![]() смещение:
смещение:
![]() , производная:
, производная: ![]() ;
;
при ![]() смещение:
смещение:
![]() , производная:
, производная: ![]() ;
;
при ![]() смещение:
смещение:
![]() , производная:
, производная: ![]() .
.
Для удобства сравнения все кривые нормированы на приведенные здесь значения смещений и производных.
Рис.4. Траектории ПМСВ (а), их
производные (б) и фазовые портреты (в) при различных значениях начального угла ![]() :
:
1 – ![]() ; 2 –
; 2 – ![]() ; 3 –
; 3 – ![]() .
.
Модуляция высоты вершины «вала»: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Частота модуляции: ![]() .
.
Остальные параметры – те же, что на рис.2.
Из рисунка видно следующее:
1) Все отдельные траектории и их производные идут по разному, отдельные фазовые траектории тоже отличаются друг от друга. Это означает, что конкретный вид траекторий и их производных зависит от угла.
2) Амплитуды и частоты колебаний нормированных сигналов и их производных при всех углах приблизительно одинаковы и характер стохастизации примерно одинаков, то есть все они от угла не зависят.
3) Фазовые портреты нормированных сигналов практически одинаковы: траектории циклов различны, но характер замазывания и общая форма огибающих изнутри и снаружи при достаточно большом количестве циклов (здесь циклов около 20) – всегда одинаковы (при условии нормирования).
4) Индивидуальные свойства траекторий зависят от начального угла, но статистические характеристики – не зависят. Это означает, что система в статистическом отношении "не помнит" начальных условий.
5) Все эти утверждения справедливы с
точностью ![]() 10%.
10%.
7. Траектории при высвечивании
Из рис.2 можно видеть, что
траектории при прохождении некоторого расстояния вдоль оси ![]() обрываются, то есть «высвечиваются». Так
траектории для смещения
обрываются, то есть «высвечиваются». Так
траектории для смещения ![]() по оси
по оси ![]() и его производной
и его производной ![]() обрываются
при
обрываются
при ![]() .
.
Рассмотрим процесс высвечивания
более подробно, для чего обратимся к рис.5, где показаны траектории производных
от смещения по координате ![]() (1) и фазовые портреты колебаний
(1) и фазовые портреты колебаний ![]() (2) при разных значениях
нормированной частоты модуляции
(2) при разных значениях
нормированной частоты модуляции
где ![]() – пространственная частота
модуляции,
– пространственная частота
модуляции, ![]() – пространственная частота траекторий в отсутствие модуляции.
– пространственная частота траекторий в отсутствие модуляции.
При построения рисунка с целью наглядности были выбраны именно траектории производных, а не смещения, так как они, как видно из рис.2б, проявляют более сильное отклонение от синусоидального режима. При этом траектории для смещения ведут себя аналогично.
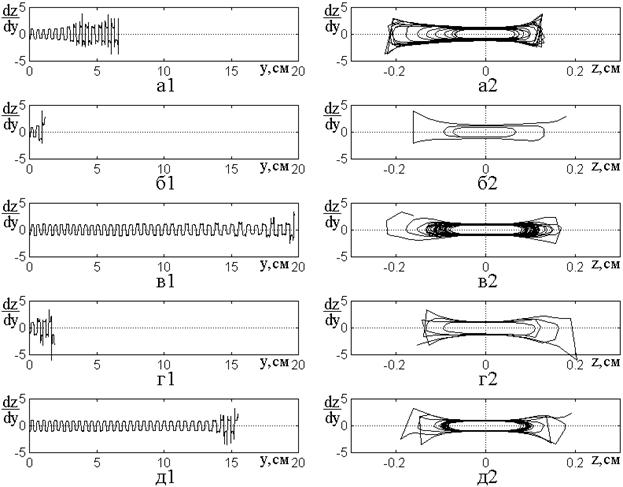
Рис.5. Развертки во времени
производных от траекторий по координате ![]() (1) и фазовые портреты колебаний
(1) и фазовые портреты колебаний ![]() (2) при разных значениях нормированной
частоты модуляции
(2) при разных значениях нормированной
частоты модуляции ![]() . Параметры – те же, что на
рис.2.
. Параметры – те же, что на
рис.2.
а – ![]() –
– ![]() ; б –
; б –
![]() –
– ![]() ;
;
в – ![]() –
– ![]() ; г
–
; г
– ![]() –
– ![]() ;
;
д – ![]() –
– ![]() .
.
Из рисунка видно, что при
различных значениях ![]() длина траектории
длина траектории ![]() сильно меняется. Так при
сильно меняется. Так при ![]() (рис.5б) ее длина составляет всего
(рис.5б) ее длина составляет всего
![]() , тогда как при
, тогда как при ![]() (рис.5в) – уже достигает
(рис.5в) – уже достигает ![]() .
.
Можно видеть, что во многих случаях (в,г) хаотизация траекторий наступает не сразу, а сначала траектория достаточно долго пребывает в «псевдосинусоидальном» режиме (для рис.5в1 более 30 периодов) и только на конечном участке, составляющем порядка 3-5 периодов, сильно хаотизируется. То есть траектории высвечиваются тогда, когда хаотизация становится достаточно интенсивной. Соответственно фазовые портреты содержат четко выраженную кольцеобразную сердцевину, соответствующую многократному прохождению по циклу квазирегулярных частей траекторий, после чего размах резко увеличивается, отдельные ветви идут в разнос и создают острые углы, после чего обрываются – высвечиваются.
8. Длина высвечивания
Как показано в предыдущем разделе, характер высвечивания траекторий ПМСВ весьма сильно зависит от частоты модуляции.
Причина высвечивания будет
рассмотрена далее, а сейчас обратимся к сравнению различных степеней хаотизации
траекторий при изменении этой частоты. В качестве критерия стохастичности
возьмем максимальную до обрыва длину траектории ![]() , которую
назовем “длиной высвечивания”. Как видно из рис.5, на протяжения этой длины
траектория сначала ведет себя более или менее регулярно, то есть, можно
сказать, пребывает в состоянии «псевдосинусоидальности» и только на конце приобретает
хаотический размах, после чего высвечивается. Таким образом, будем считать, что
стохастичность выражена тем сильнее, чем меньше траектория пребывает в
состоянии «псевдосинусоидальности», то есть чем скорее высвечивается или длина
высвечивания становится меньше.
, которую
назовем “длиной высвечивания”. Как видно из рис.5, на протяжения этой длины
траектория сначала ведет себя более или менее регулярно, то есть, можно
сказать, пребывает в состоянии «псевдосинусоидальности» и только на конце приобретает
хаотический размах, после чего высвечивается. Таким образом, будем считать, что
стохастичность выражена тем сильнее, чем меньше траектория пребывает в
состоянии «псевдосинусоидальности», то есть чем скорее высвечивается или длина
высвечивания становится меньше.
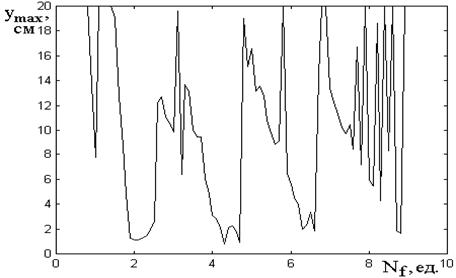
Рис.6. Зависимость длины высвечивания траекторий от относительной частоты модуляции.
На рис.6 показана длина высвечивания
траекторий ![]() , для разных пространственных частот модуляции
, для разных пространственных частот модуляции ![]() . При этом:
. При этом: ![]() , где
, где ![]() – пространственная частота
траекторий в отсутствие модуляции. Наблюдаемая сильная изрезанность зависимости
– пространственная частота
траекторий в отсутствие модуляции. Наблюдаемая сильная изрезанность зависимости
![]() от
от ![]() отражает частичный пространственный синхронизм
траекторий ПМСВ и поля. Величина
отражает частичный пространственный синхронизм
траекторий ПМСВ и поля. Величина ![]() минимальна, когда период ПМСВ
близок к целому числу периодов модуляции, причем наиболее глубокие минимумы
соответствуют их четному числу (2, 4, 6, 8). Так, при
минимальна, когда период ПМСВ
близок к целому числу периодов модуляции, причем наиболее глубокие минимумы
соответствуют их четному числу (2, 4, 6, 8). Так, при ![]() длина траектории ПМСВ равна
длина траектории ПМСВ равна ![]() , при
, при ![]() –
– ![]() , при
, при ![]() –
– ![]() , тогда
как при
, тогда
как при ![]() –
– ![]() , при
, при ![]() –
– ![]() , при
, при ![]() –
– ![]() , что
значительно большое этих величин при четных
, что
значительно большое этих величин при четных ![]() . При
целых значениях
. При
целых значениях ![]() траектория ПМСВ пересекает вершину «вала» (ось
траектория ПМСВ пересекает вершину «вала» (ось ![]() ) всего четыре-пять раз. В промежутках
между целыми значениями
) всего четыре-пять раз. В промежутках
между целыми значениями ![]() длина траекторий ПМСВ может достигать
длина траекторий ПМСВ может достигать ![]() . При
. При ![]() вплоть до
вплоть до ![]() минимумы
минимумы ![]() обнаружены не были.
обнаружены не были.
9. Фрактальный характер высвечивания
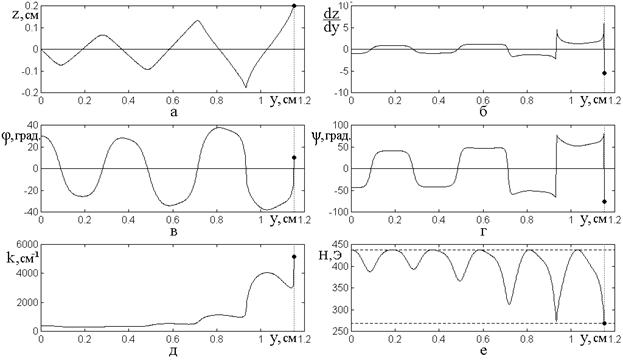
Рассмотрим теперь, как ведут себя другие параметры ПМСВ в точке высвечивания, для чего обратимся к рис.7, где показаны зависимости предельных значений этих параметров от нормированной частоты модуляции.

Рис.7. Зависимости различных параметров траекторий от нормированной частоты модуляции. Модуляция крутизны склонов «вала».
Параметры – те же, что на рис.2.
На рис.7 показаны
характеристики траекторий ПМСВ в зависимости от нормированной частоты модуляции
![]() , где
, где ![]() –
истинная частота модуляции, а
–
истинная частота модуляции, а ![]() – пространственная частота
траекторий ПМСВ в отсутствие модуляции. Кривая на рис.7а соответствует
максимальной (до высвечивания) длине траекторий ПМСВ
– пространственная частота
траекторий ПМСВ в отсутствие модуляции. Кривая на рис.7а соответствует
максимальной (до высвечивания) длине траекторий ПМСВ ![]() ,
построенной при условии
,
построенной при условии ![]() . Кривая на рис.7б –
достигаемому при
. Кривая на рис.7б –
достигаемому при ![]() значению волнового числа
значению волнового числа ![]() , кривая на рис.7в – значению поля
, кривая на рис.7в – значению поля ![]() и кривая на рис.7г – значению угла
и кривая на рис.7г – значению угла ![]() .
.
Из рисунка видно, что все
кривые сильно изрезаны, в соответствии со стохастическим характером траекторий
ПМСВ и их высвечивания. По характеру кривых весь интервал изменения ![]() можно разбить на 9 областей, номера которых
приведены сверху на рисунке. Из рис.7а видно, что длина
можно разбить на 9 областей, номера которых
приведены сверху на рисунке. Из рис.7а видно, что длина ![]() испытывает
близкие к периодическим спады и подъемы, достигая минимумов (в областях 2, 4,
6, 8), когда период ПМСВ близок к целому четному числу периодов модуляции (2,
4, 6, 8), и максимумов (в областях 1, 3, 5, 7, 9), когда период ПМСВ близок к
нечетному числу периодов модуляции (1, 3, 5, 7, 9). Эта кривая близка к
представленной на рис.6. Так, при
испытывает
близкие к периодическим спады и подъемы, достигая минимумов (в областях 2, 4,
6, 8), когда период ПМСВ близок к целому четному числу периодов модуляции (2,
4, 6, 8), и максимумов (в областях 1, 3, 5, 7, 9), когда период ПМСВ близок к
нечетному числу периодов модуляции (1, 3, 5, 7, 9). Эта кривая близка к
представленной на рис.6. Так, при ![]() длина траектории ПМСВ
превышает
длина траектории ПМСВ
превышает ![]() , при
, при ![]() составляет
всего
составляет
всего ![]() , при
, при ![]() достигает
достигает
![]() , при
, при ![]() снижается
до
снижается
до ![]() , при
, при ![]() возрастает
до
возрастает
до ![]() , при
, при ![]() снова
уменьшается до
снова
уменьшается до ![]() и так далее. В областях минимумов
и так далее. В областях минимумов
![]() (2, 4, 6, 8) волновое число
(2, 4, 6, 8) волновое число ![]() (рис.7б), как правило составляет
(рис.7б), как правило составляет ![]() , что особенно хорошо заметно для области
2, а в областях максимумов
, что особенно хорошо заметно для области
2, а в областях максимумов ![]() (1, 3, 5, 7, 9)
значительно меньше (
(1, 3, 5, 7, 9)
значительно меньше (![]() ). Значения поля
). Значения поля ![]() (рис.7в) в областях минимумов
(рис.7в) в областях минимумов ![]() (2, 4, 6, 8) не превышает
(2, 4, 6, 8) не превышает ![]() , тогда как в областях максимумов
, тогда как в областях максимумов ![]() (1, 3, 5, 7, 9), - достигает
(1, 3, 5, 7, 9), - достигает ![]() и более. Значения углов
и более. Значения углов ![]() (рис.7г) заметной корреляции с частотой
модуляции не проявляют.
(рис.7г) заметной корреляции с частотой
модуляции не проявляют.
Наблюдаемая сильная изрезанность
кривых на рис.7 побудила исследовать зависимость характера этой изрезанности от
величины шага по частоте модуляции. Полученные результаты иллюстрируются рис.8,
где показаны зависимости максимальной (до высвечивания) длины траекторий ПМСВ ![]() , от нормированной частоты модуляции
, от нормированной частоты модуляции ![]() при различном шаге по
при различном шаге по ![]() . Рис.8а соответствует интервалу
. Рис.8а соответствует интервалу ![]() , проходимому с шагом в
, проходимому с шагом в ![]() . Рис.8б соответствует начальному участку
того же интервала при
. Рис.8б соответствует начальному участку
того же интервала при ![]() , проходимому с шагом
в
, проходимому с шагом
в ![]() . Рис.8в соответствует еще меньшему
начальному участку того же интервала при
. Рис.8в соответствует еще меньшему
начальному участку того же интервала при ![]() ,
проходимому с шагом в
,
проходимому с шагом в ![]() .
.

Рис.8. Зависимости длины
высвечивания от нормированной частоты модуляции, снятые при различной величине
шага по частоте ![]() :
:
а – ![]() ; б –
; б – ![]() ; в –
; в – ![]() .
.
Из сравнения рисунков видно,
что при уменьшении интервала изменения ![]() на два
порядка характер изрезанности зависимости
на два
порядка характер изрезанности зависимости ![]() (размах
по вертикальной оси, крутизна склонов) практически не меняется, то есть эта зависимость
проявляет фракталоподобные свойства (аналогичные, например, свойствам береговой
линии материков [24]). Аналогичное исследование зависимостей
(размах
по вертикальной оси, крутизна склонов) практически не меняется, то есть эта зависимость
проявляет фракталоподобные свойства (аналогичные, например, свойствам береговой
линии материков [24]). Аналогичное исследование зависимостей ![]() ,
, ![]() и
и ![]() также выявляет их фрактальный характер.
Причиной таких свойств высвечивания траекторий ПМСВ, распространяющихся в
неоднородном поле типа "вала" с периодической модуляцией, очевидно,
является их стохастическая неустойчивость.
также выявляет их фрактальный характер.
Причиной таких свойств высвечивания траекторий ПМСВ, распространяющихся в
неоднородном поле типа "вала" с периодической модуляцией, очевидно,
является их стохастическая неустойчивость.
10. Природа высвечивания
Рассмотрим теперь несколько
подробнее физический механизм высвечивания, для чего обратимся к рис.9, где
показаны зависимости различных параметров распространяющейся волны от продольной
координаты ![]() .
.
Для наиболее наглядного
выявления картины высвечивания здесь рассмотрен случай минимальной длины
траектории по координате ![]() , соответствующий
частоте модуляции поля
, соответствующий
частоте модуляции поля ![]() в два раза большей пространственной частоты траекторий
в отсутствие модуляции
в два раза большей пространственной частоты траекторий
в отсутствие модуляции ![]() , то есть
, то есть ![]() , где
, где ![]() . Из рис.6 можно видеть, что эта частота
как раз соответствует первому минимуму зависимости
. Из рис.6 можно видеть, что эта частота
как раз соответствует первому минимуму зависимости ![]() от
от ![]() .
.
Рис.9. Зависимости от координаты ![]() различных параметров распространяющейся
волны вблизи области высвечивания.
различных параметров распространяющейся
волны вблизи области высвечивания.
Вертикальная точечная линия –
координата ![]() , соответствующая высвечиванию.
Укрупненные точки – окончания соответствующих зависимостей.
, соответствующая высвечиванию.
Укрупненные точки – окончания соответствующих зависимостей.
а – смещение; б – производная от смещения;
в – угол фазовой скорости; г – угол групповой скорости;
д – волновое число; е – поле.
На рис.9а и 9б показаны траектория и ее производная вплоть до момента высвечивания, обозначенного укрупненной точкой. Видно, что кроме определенной нерегулярности, в известной степени нарушающей их квазипериодичность, никаких серьезных особенностей эти зависимости не проявляют.
На рис.9в и 9г показаны углы,
которые составляют векторы фазовой и групповой скоростей с осью ![]() по мере распространения волны. Обе
зависимости также имеют квазипериодический характер с постепенным нарастанием
отклонения от периодичности. Зависимость
по мере распространения волны. Обе
зависимости также имеют квазипериодический характер с постепенным нарастанием
отклонения от периодичности. Зависимость ![]() заканчивается
при
заканчивается
при ![]() , зависимость
, зависимость ![]() – при
– при ![]() . Таким образом, здесь серьезных
особенностей также не наблюдается.
. Таким образом, здесь серьезных
особенностей также не наблюдается.
Однако из рис.9д видно, что
волновое число, по мере распространения волны, в общем, увеличивается, причем
при координате ![]() , соответствующей высвечиванию,
составляет
, соответствующей высвечиванию,
составляет ![]() , что почти на порядок превышает начальное
значение при
, что почти на порядок превышает начальное
значение при ![]() равное
равное ![]() .
.
Из рис.9е видно, что значение
поля ![]() , соответствующие координате
, соответствующие координате ![]() , соответствующей высвечиванию, составляет
, соответствующей высвечиванию, составляет
![]() .
.
С другой стороны, поле,
соответствующее начальной точке волны ![]() , равно
, равно
![]() , причем в соответствии с законом
модуляции (13)-(14) это поле на всей площади ферритовой пластины может только
уменьшаться. Частоте
, причем в соответствии с законом
модуляции (13)-(14) это поле на всей площади ферритовой пластины может только
уменьшаться. Частоте ![]() , на которой происходит
возбуждение ПМСВ, соответствует минимальное поле
, на которой происходит
возбуждение ПМСВ, соответствует минимальное поле ![]() [20],
то есть в областях пластины, где величина поля ниже этого значения, волна
существовать не может. Этому полю соответствует асимптотическое стремление
волнового числа к бесконечности.
[20],
то есть в областях пластины, где величина поля ниже этого значения, волна
существовать не может. Этому полю соответствует асимптотическое стремление
волнового числа к бесконечности.
Как видим, поле ![]() , имеющее место в точке
, имеющее место в точке ![]() , отличается от предельного значения
, отличается от предельного значения ![]() всего на
всего на ![]() , то
есть на
, то
есть на ![]() . С другой стороны, из рис.9д видно, что
волновое число в этом же поле достигает значения
. С другой стороны, из рис.9д видно, что
волновое число в этом же поле достигает значения ![]() , то
есть проявляет тенденцию к бесконечному увеличению.
, то
есть проявляет тенденцию к бесконечному увеличению.
Таким образом, можно полагать, что высвечивание траектории ПМСВ происходит тогда, когда она попадает в такое место ферритовой пластины, где поле имеет значение, соответствующее границе спектра ПМСВ, причем на этой границе волновое число стремится к бесконечности.
ЗАМЕЧАНИЕ. В работах [12-19],
хотя и без достаточного обоснования, но утверждается, что высвечивание
обусловлено достижением угла ![]() значения отсечки, что
в свете сказанного нельзя считать полностью верным. Действительно, в
рассмотренных здесь условиях угол отсечки на частоте
значения отсечки, что
в свете сказанного нельзя считать полностью верным. Действительно, в
рассмотренных здесь условиях угол отсечки на частоте ![]() в
поле
в
поле ![]() составляет
составляет![]() , а в
поле
, а в
поле ![]() –
– ![]() . Между
этими полями угол отсечки принимает промежуточные значения. Как можно видеть из
рис.9в, значение угла
. Между
этими полями угол отсечки принимает промежуточные значения. Как можно видеть из
рис.9в, значение угла ![]() в точке высвечивания по
абсолютной величине составляет
в точке высвечивания по
абсолютной величине составляет ![]() , что не соответствует
ни одному из приведенных крайних значений. Это происходит потому, что
действительной причиной высвечивания является не достижение угла отсечки, а
выход траектории за допустимую нижнюю полевую границу существования ПМСВ, что
сопровождается бесконечным увеличением волнового числа.
, что не соответствует
ни одному из приведенных крайних значений. Это происходит потому, что
действительной причиной высвечивания является не достижение угла отсечки, а
выход траектории за допустимую нижнюю полевую границу существования ПМСВ, что
сопровождается бесконечным увеличением волнового числа.
Заметим однако, что близость
угла ![]() к углу отсечки сопровождается бесконечным
ростом волнового числа, то есть хотя первичной наблюдаемой причиной
высвечивания остается увеличение волнового числа, но и приближение к углу
отсечки при этом вполне может иметь место, как это и было отмечено в работе [16].
к углу отсечки сопровождается бесконечным
ростом волнового числа, то есть хотя первичной наблюдаемой причиной
высвечивания остается увеличение волнового числа, но и приближение к углу
отсечки при этом вполне может иметь место, как это и было отмечено в работе [16].
11. Характер траекторий при различных видах модуляции
Описанная в предыдущих разделах стохастическая неустойчивость траекторий ПМСВ наблюдается при модуляции не только крутизны склонов, но также высоты и сдвига вершины «вала». Следуя [14,15], рассмотрим этот вопрос более подробно.
11.1. Критерий длины высвечивания
Возьмем все параметры теми же, что
при построении рис.2б, кроме начального угла ![]() между волновым вектором и осью
между волновым вектором и осью ![]() , который для удобства наблюдения
высвечивания положим близким к углу отсечки:
, который для удобства наблюдения
высвечивания положим близким к углу отсечки: ![]() ,
,
Сравним теперь эффективность
различных видов модуляции, пользуясь зависимостями длины высвечивания ![]() от коэффициента глубины модуляции
от коэффициента глубины модуляции ![]() , показанными на рис.4.
, показанными на рис.4.
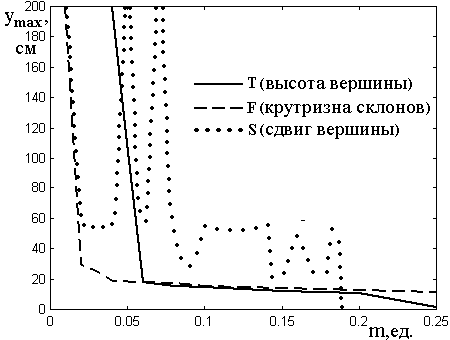
Рис.10. Зависимость длины
высвечивания от глубины модуляции при различных ее видах. Сплошная кривая
соответствует модуляции высоты вершины «вала» ![]() ,
пунктирная – крутизны склонов
,
пунктирная – крутизны склонов ![]() , и точечная – сдвига
вершины «вала»
, и точечная – сдвига
вершины «вала» ![]() .
.
Параметры – те же, что на
рис.2,
кроме ![]() .
.
Из рис.10 видно, что общим
свойством всех кривых является резкий (практически скачкообразный) спад длины
высвечивания при некоторых значениях глубины модуляции. Для зависимостей ![]() и
и ![]() этот
спад наблюдается при
этот
спад наблюдается при ![]() и
и ![]() соответственно,
после чего обе зависимости плавно стремятся к нулю. Зависимость
соответственно,
после чего обе зависимости плавно стремятся к нулю. Зависимость ![]() не является монотонной и при общей
тенденции снижения претерпевает несколько резких спадов (при
не является монотонной и при общей
тенденции снижения претерпевает несколько резких спадов (при ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ) и подъемов (при
) и подъемов (при ![]() ,
,
![]() ,
, ![]() ,
, ![]() и
и ![]() ). На
этой зависимости выделяются два значения длины высвечивания -
). На
этой зависимости выделяются два значения длины высвечивания - ![]() и
и ![]() , соответствующие
нескольким плоским участкам, между которыми длина высвечивания меняется резко.
Такой ступенчатый со скачкообразными переходами вид приведенных зависимостей
наводит на мысль о пороговом характере явления, что однако требует дополнительной
проверки (выходит за рамки данной статьи).
, соответствующие
нескольким плоским участкам, между которыми длина высвечивания меняется резко.
Такой ступенчатый со скачкообразными переходами вид приведенных зависимостей
наводит на мысль о пороговом характере явления, что однако требует дополнительной
проверки (выходит за рамки данной статьи).
Далее из рис.10 можно видеть,
что ниже всех проходит кривая, соответствующая модуляции крутизны склонов
«вала» (![]() ), то есть в этом случае высвечивание
наступает при наименьшем значении глубины модуляции. Кривая, соответствующая
модуляции высоты вершины (
), то есть в этом случае высвечивание
наступает при наименьшем значении глубины модуляции. Кривая, соответствующая
модуляции высоты вершины (![]() ), занимает среднее
положение, а кривая, соответствующая сдвигу вершины (
), занимает среднее
положение, а кривая, соответствующая сдвигу вершины (![]() ),
проходит наиболее высоко, что соответствует наибольшему требуемому для высвечивания
значению глубины модуляции.
),
проходит наиболее высоко, что соответствует наибольшему требуемому для высвечивания
значению глубины модуляции.
Таким образом, сравнение эффективности различных видов модуляции по критерию минимальности длины высвечивания показывает, что наиболее эффективной является модуляция крутизны склонов «вала», несколько менее эффективной – вершины «вала» и наименее эффективной – сдвига вершины «вала».
11.2. Критерий развития в пространстве
Рассмотрим теперь особенности
стохастизации траекторий ПМСВ при различных видах модуляции более подробно на
основе их развития в пространстве. Оставим все параметры теми же, что при построении
рис.10, в том числе, чтобы наблюдать траектории на большем отрезке времени,
отойдем от угла отсечки и возьмем ![]() . Будем рассматривать
следующие виды модуляции параметров «вала»: высоты вершины
. Будем рассматривать
следующие виды модуляции параметров «вала»: высоты вершины ![]() ; крутизны склонов
; крутизны склонов ![]() ;
сдвига вершины
;
сдвига вершины ![]() .
.
Результаты рассмотрения
иллюстрируется рис.11, где представлены: а – траектории ПМСВ ![]() ; б – производные от траекторий по
координате
; б – производные от траекторий по
координате ![]() –
– ![]() ; в –
фазовые портреты как зависимости
; в –
фазовые портреты как зависимости ![]() от
от ![]() . Цифры соответствуют различным видам
модуляции поля: 1 – модуляция отсутствует; 2 – модулируется высота вершины
«вала» (параметр
. Цифры соответствуют различным видам
модуляции поля: 1 – модуляция отсутствует; 2 – модулируется высота вершины
«вала» (параметр ![]() ); 3 – модулируется крутизна
склонов «вала» (параметр
); 3 – модулируется крутизна
склонов «вала» (параметр ![]() ); 4 – модулируется
сдвиг вершины «вала» (параметр
); 4 – модулируется
сдвиг вершины «вала» (параметр ![]() ).
).
При построении приведенных на
рис.11 зависимостей, с целью возможности сравнения эффективности различных
видов модуляции, величины коэффициентов ![]() ,
, ![]() и
и ![]() были
подобраны таким образом, чтобы максимальные отклонения значения поля при координате
были
подобраны таким образом, чтобы максимальные отклонения значения поля при координате
![]() для всех видов модуляции были бы одинаковыми.
При этом в отсутствие модуляции поле вершины «вала» составляло
для всех видов модуляции были бы одинаковыми.
При этом в отсутствие модуляции поле вершины «вала» составляло ![]() , а поле при
, а поле при ![]() равнялось
равнялось
![]() . В результате каждого из видов модуляции
поле при
. В результате каждого из видов модуляции
поле при ![]() уменьшалось от
уменьшалось от ![]() до
до
![]() , то есть на
, то есть на ![]() .
Значения параметров модуляции, требуемые для таких изменений поля, следующие:
.
Значения параметров модуляции, требуемые для таких изменений поля, следующие: ![]() ,
, ![]() и
и ![]() .
.
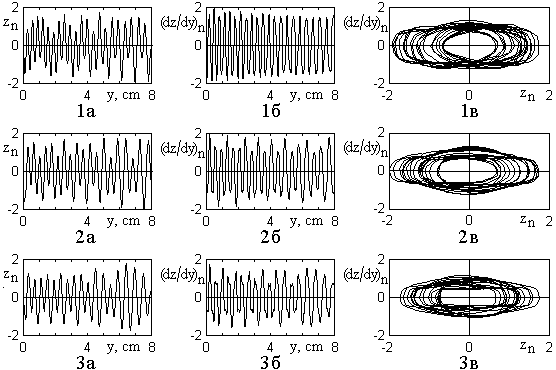
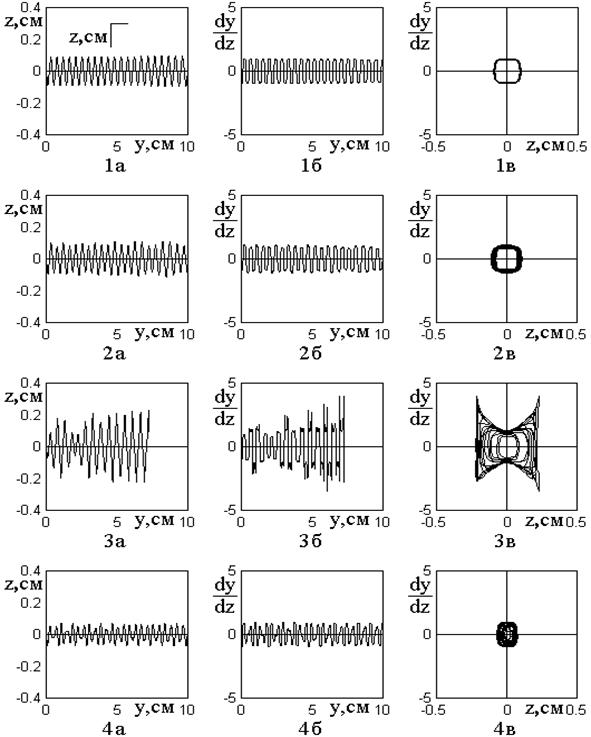
Рис.11. Развитие во времени траектории (а) и ее производной (б), а также фазовые портреты (в) при различных видах модуляции.
Основные параметры: ![]() ;
; ![]() ;
; ![]() ;
;
параметры модуляции: высоты
вершины: ![]() ; крутизны склонов:
; крутизны склонов: ![]() ; сдвига вершины:
; сдвига вершины: ![]() .
.
Из рис.11 видно следующее:
1) В отсутствие модуляции как траектория (1а), так и ее производная (1б) – почти правильные синусоиды с постоянной амплитудой, фазовый портрет (1в) – точно повторяющийся цикл в виде прямоугольника с закругленными углами. Некоторая видимая ширина контуров цикла (менее 5% от его диаметра) обусловлена погрешностью машинного расчета и с уменьшением шага интегрирования уменьшается.
2) При наличии модуляции любого вида наблюдается стохастическая неустойчивость траекторий (2а-4а) и их производных (2б-4б), проявляющаяся в случайном изменении амплитуды, частоты и фазы кривых. При этом фазовый портрет сильно размазывается – фазовая траектория в течение каждого цикла описывает новую кривую (2в-4в).
3) Величина скачков амплитуды
при модуляции высоты вершины «вала» достигает 20-30%, при модуляции крутизны
склонов «вала» – 200-300%, при модуляции сдвига вершины «вала» – 50-60%. Размазанность
фазового портрета составляет ту же величину. При этом скачки амплитуды при
модуляции высоты и сдвига вершины «вала», как правило, происходят в сторону ее
уменьшения, в результате чего фазовый портрет замазывается внутрь относительно
устойчивого цикла. При модуляции крутизны склонов «вала», скачки амплитуды, происходят
в сторону ее увеличения, в результате чего фазовый портрет замазывается наружу
относительно устойчивого цикла. При этом он, во-первых, расширяется в 2-3 раза
по координате ![]() и, во-вторых, на его углах
появляются сильно выраженные «острия», направленные вдоль производной
и, во-вторых, на его углах
появляются сильно выраженные «острия», направленные вдоль производной ![]() .
.
4) При модуляции крутизны
склонов «вала» (3) высвечивание траектории происходит при ![]() . При модуляции высоты (2) и сдвига
вершины «вала» (4) высвечивание вплоть до
. При модуляции высоты (2) и сдвига
вершины «вала» (4) высвечивание вплоть до ![]() отсутствует
и происходит не ранее, чем при
отсутствует
и происходит не ранее, чем при ![]() .
.
11.3. Фазовые портреты в крупном масштабе
На рис.12 показаны отдельно фазовые портреты при разных видах модуляции в крупном масштабе, позволяющем более подробно разглядеть их детали.
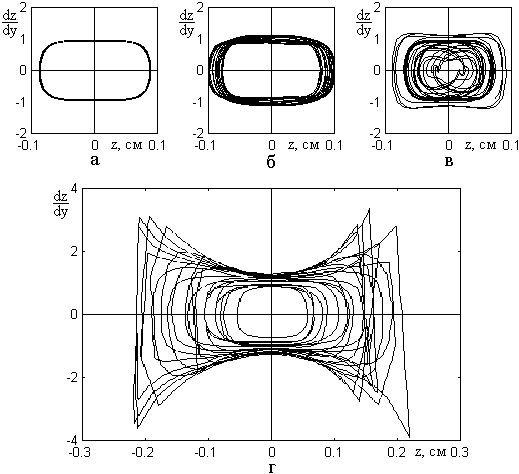
Рис.12. Фазовые портреты при разных видах модуляции.
а – модуляция отсутствует;
б – модулируется высота вершины
"вала" (параметр ![]() );
);
в – модулируется сдвиг вершины
"вала" (параметр ![]() );
);
г – модулируется крутизна склонов
"вала" (параметр ![]() ).
).
Параметры – те же, что на рис.11.
Рис.12а соответствует отсутствию модуляции и приведен здесь для сравнения. Видно, что в этом случае фазовый портрет представляет собой плавное узкое кольцо, что говорит о полной повторяемости колебаний от периода к периоду.
Рис.12б соответствует модуляции
высоты вершины «вала». В этом случае неустойчивость траекторий уже начинает
проявляться, однако еще в сравнительно небольшой степени: фазовый портрет опять
представляет собой почти правильное кольцо, однако теперь его образующие
относительно диаметра расширены на ![]() . Внутри кольца
наблюдается большая свободная от траекторий «сердцевина», размер которой составляет
около
. Внутри кольца
наблюдается большая свободная от траекторий «сердцевина», размер которой составляет
около ![]() от внешнего диаметра кольца.
от внешнего диаметра кольца.
Рис.12в соответствует модуляции
сдвига вершины «вала». Четко проявляется перемещение значительного числа
траекторий с периферии кольца к его внутренней части, однако наружная огибающая
остается достаточно плавной. Свободная от траекторий сердцевина значительно
сужается и в поперечнике составляет не более ![]() от
внешнего диаметра.
от
внешнего диаметра.
Рис.12г соответствует модуляции
крутизны склонов «вала». В этом случае хаотизация траекторий проявляется
наиболее сильно. Наружная огибающая портрета приобретает сильно изрезанный
характер с ярко выраженными острыми выбросами на углах портрета, приходящихся
на его диагонали. Общие размеры портрета по сравнению с предыдущими случаями увеличиваются
более чем в два раза, однако в середине портрета, соответствующей нулевому
значению координаты ![]() , появляется перетяжка, где
размер по производной увеличивается не более чем на
, появляется перетяжка, где
размер по производной увеличивается не более чем на ![]() .
Свободная от траекторий сердцевина значительно увеличивается, ее размер по
координате достигает
.
Свободная от траекторий сердцевина значительно увеличивается, ее размер по
координате достигает ![]() , а по производной доходит до
, а по производной доходит до ![]() от внешнего диаметра.
от внешнего диаметра.
Таким образом, как следует из рис.11 и 12, анализ развития траекторий в пространстве показывает, что их стохастизация наблюдается при модуляции любого вида, однако сильнее всего она проявляется при модуляции крутизны склонов «вала», заметно слабее при модуляции высоты вершины «вала» и еще слабее при модуляции сдвига его вершины. Такое поведение полностью совпадает с характером стохастизации, полученным ранее на основе критерия минимальности высвечивания (рис.10).
12. Изменение частоты возбуждения ПМСВ
Проведенное выше рассмотрение
касается возбуждения ПМСВ на единственной частоте ![]() .
Однако, как можно видеть из анализа дисперсионного соотношения (3), как
фазовая, так и групповая скорости ПМСВ при изменении частоты сильно меняются,
что сказывается на форме траекторий.
.
Однако, как можно видеть из анализа дисперсионного соотношения (3), как
фазовая, так и групповая скорости ПМСВ при изменении частоты сильно меняются,
что сказывается на форме траекторий.
Рис.13. Траектории ПМСВ (а), их производные (б), зависимости волнового числа от координаты (в) и фазовые портреты (г) при различных значениях частоты.
1 – ![]() ; 2 –
; 2 – ![]() ; 3 –
; 3 – ![]() .
.
Параметры – те же, что на рис.2.
Рассмотрим теперь, как меняется
характер хаотизации траекторий ПМСВ при изменения частоты возбуждения, для чего
обратимся к рис.13, где показаны траектории ПМСВ (а), их производные (б),
зависимости волнового числа от координаты (в) и фазовые портреты (г) при
различных значениях частоты ПМСВ. Вертикальными точечными линиями показаны
значения координаты ![]() , при которой происходит
высвечивание траекторий. Частоте
, при которой происходит
высвечивание траекторий. Частоте ![]() (1) соответствует
(1) соответствует ![]() (точка высвечивания находится далеко за
правым краем рисунка), частоте
(точка высвечивания находится далеко за
правым краем рисунка), частоте ![]() (2) –
(2) – ![]() , частоте
, частоте ![]() (3) –
(3) – ![]() . При этом верхняя граница спектра ПМСВ
здесь равна
. При этом верхняя граница спектра ПМСВ
здесь равна ![]() .
.
Из рисунка видно, что
высвечивание происходит при тем меньшем значении ![]() , чем
ближе частота ПМСВ к своему верхнему пределу.
, чем
ближе частота ПМСВ к своему верхнему пределу.
Все траектории (рис.13а) имеют вид, близкий к пилообразному с симметричными зубцами, однако на нижней из выбранных частот (а1) вершины зубцов довольно закругленные, тогда как на средней (а2) и тем более высшей (а3) частоте вершины становятся тем острее, чем выше частота.
Это свойство особенно сильно проявляется на зависимостях для производных (рис.13б), так на низшей частоте (2а) кривые в местах закруглений ведут себя довольно плавно, на средней (2б) – уже на третьем периоде проявляются острые выбросы, на высшей частоте (2г) резкие выбросы происходят уже с самого начала траектории.
Волновое число (рис.13в) во
всех случаях по мере увеличения координаты ![]() имеет
тенденцию к повышению. С повышением частоты как само волновое число, так и его
рост по координате увеличиваются. Так на низшей частоте (в1) в пределах рисунка
волновое число меняется от
имеет
тенденцию к повышению. С повышением частоты как само волновое число, так и его
рост по координате увеличиваются. Так на низшей частоте (в1) в пределах рисунка
волновое число меняется от ![]() до
до ![]() . На средней частоте (в2) волновое число
меняется от
. На средней частоте (в2) волновое число
меняется от ![]() до
до ![]() , на
верхней (в3) – возрастает с
, на
верхней (в3) – возрастает с ![]() до
до ![]() .
.
Такой рост волнового числа
соответствует приближению угла ![]() волнового вектора ПМСВ
к углу отсечки, при котором волновое число асимптотически стремится к бесконечности.
волнового вектора ПМСВ
к углу отсечки, при котором волновое число асимптотически стремится к бесконечности.
Фазовый портрет (рис.13г), имея на низшей частоте (г1) вид довольно округлого кольца, на средней (г2) уже на одной стороне приобретает два острых угла, тогда как на высшей (г3) резко выраженные острые углы появляются на обеих сторонах. Такой вид фазового портрета с ростом острых углов по мере увеличения частоты отражает увеличение резких выбросов на производных от траекторий (б), отмеченное выше.
13. Некоторые дополнительные особенности неустойчивости траекторий
Отметим еще некоторые достаточно общие особенности неустойчивости траекторий ПМСВ.
1) Неустойчивость проявляется
тем сильнее, чем больше глубина модуляции. Так при начальном значении угла ![]() и глубине модуляции
и глубине модуляции ![]() на частоте
на частоте ![]() длина
высвечивания равна
длина
высвечивания равна ![]() , а при
, а при ![]() уменьшается
до
уменьшается
до ![]() .
.
2) Неустойчивость проявляется
тем сильнее, чем ближе частота ПМСВ к своему верхнему пределу. Так при
начальном угле ![]() и
и ![]() такой
предел равен
такой
предел равен ![]() . При этом на частоте
. При этом на частоте ![]() величина
величина ![]() составляет
составляет
![]() , при частоте
, при частоте ![]() –
– ![]() , а при частоте
, а при частоте ![]() –
–
![]() . Однако из такой зависимости иногда наблюдаются
исключения. Так при
. Однако из такой зависимости иногда наблюдаются
исключения. Так при ![]() и частоте
и частоте ![]() величина
величина ![]() составляет
составляет
![]() , а при частоте
, а при частоте ![]() уменьшается
до
уменьшается
до ![]() . Тем не менее, в общем, отмеченное
уменьшение
. Тем не менее, в общем, отмеченное
уменьшение ![]() при увеличении частоты ПМСВ, как правило,
сохраняется.
при увеличении частоты ПМСВ, как правило,
сохраняется.
3) Неустойчивость усиливается
при приближении начального значения ![]() к углу отсечки. Так,
на частоте
к углу отсечки. Так,
на частоте ![]() угол отсечки близок к
угол отсечки близок к ![]() . При этом, если
. При этом, если ![]() ,
то при начальном значении угла
,
то при начальном значении угла ![]() величина
величина ![]() составляет
составляет ![]() , при
, при ![]() –
– ![]() , а при
, а при
![]() – всего
– всего ![]() .
.
Приведенные особенности охарактеризованы здесь лишь схематично, более подробное исследование показывает, что отмеченные зависимости от глубины модуляции, частоты и угла отсечки, хотя и выполняются в общем, но, как правило, не являются монотонными, а заметно изрезаны, причем, возможно, имеют фрактальный характер. Более точное выяснение этого вопроса требует дополнительного исследования и выходит за рамки настоящей работы.
14. К вопросу о механизме стохастизации траекторий
Проведенное рассмотрение, в основном, представляет собой описание явлений, сопровождающих распространение ПМСВ в условиях поля типа «вала» с пространственной модуляцией. При этом показано, что траектории ПМСВ в процессе своего распространения имеют стохастический характер. Теперь рассмотрим возможный механизм такого их поведения.
Вообще говоря, описанная картина стохастизации траекторий ПМСВ в определенной степени напоминает движение частицы в «перемешивающем биллиарде», частным случаем которого является двумерный волноводный канал типа «стадиона» [1]. Отличием от классического движения механической частицы здесь является закон дисперсии ПМСВ (3), в соответствии с которым направления векторов фазовой и групповой скоростей волны могут существенно различаться (рис.1, врезка), что приводит к определенной специфике законов отражения и преломления для ПМСВ, не совпадающей со спецификой поведения механических частиц [25-27].
В задаче о биллиардах причиной стохастизации является тот факт, что в процессе отражения частицы (или луча) от выпуклой поверхности при малом изменении угла падения угол отражения меняется на значительно большую величину. Такие многократные отражения приводят в конце концов к потере памяти о начальном условии, что и проявляется как стохастизация траектории.
Таким образом, в задаче о биллиардах ключевым моментом является большое изменение выходного параметра при малом изменении входного.
В рассматриваемой здесь задаче о распространении ПМСВ такое обстоятельство также имеет место.
Так вблизи верхней границы спектра дисперсионная кривая для ПМСВ асимптотически приближается к этому верхнему пределу, в результате чего малые изменения частоты или поля могут приводить к весьма большим изменениям волнового числа.
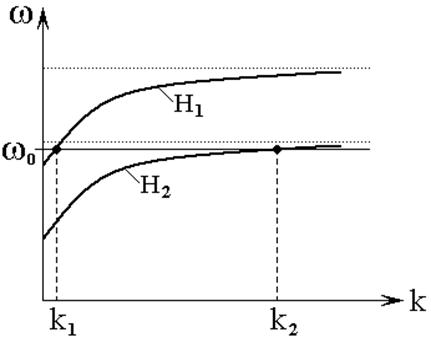
Рис.14. Схема формирования значения волнового числа при различных значениях поля.
Сказанное иллюстрируется рис.14,
где показана схема формирования значения волнового числа при различных
значениях поля. Утолщенные сплошные линии – дисперсионные кривые ПМСВ при значениях
поля ![]() и
и ![]() ,
причем
,
причем ![]() [20]. Точечными горизонтальными линиями
показаны верхние граничные частоты спектра ПМСВ, соответствующие упомянутым
полям. Сплошной горизонтальной линией отмечено заданное значение частоты
возбуждения ПМСВ. Вертикальными пунктирными линиями отмечены значения волновых
чисел, соответствующие этой частоте при полях
[20]. Точечными горизонтальными линиями
показаны верхние граничные частоты спектра ПМСВ, соответствующие упомянутым
полям. Сплошной горизонтальной линией отмечено заданное значение частоты
возбуждения ПМСВ. Вертикальными пунктирными линиями отмечены значения волновых
чисел, соответствующие этой частоте при полях ![]() и
и ![]() . Видно, что меньшему значению поля
. Видно, что меньшему значению поля ![]() соответствует большее значение волнового
числа
соответствует большее значение волнового
числа ![]() . Таким образом, поскольку поле меняется
только вниз от значения
. Таким образом, поскольку поле меняется
только вниз от значения ![]() , соответствующего
отсутствию модуляции, то и волновое число меняется только вверх от значения
, соответствующего
отсутствию модуляции, то и волновое число меняется только вверх от значения ![]() , что и наблюдается на рис.9д.
, что и наблюдается на рис.9д.
Далее из рисунка видно, что благодаря весьма пологому ходу дисперсионной кривой при достаточно больших волновых числах, малое изменение поля или частоты в этой области может приводить к весьма значительному изменению волнового числа, что и может явиться причиной «забывания» системой начальных условий и как следствие – рассмотренной хаотизации траекторий ПМСВ.
15. Замечание о машинном расчете
С практической стороны следует отметить одно важное обстоятельство, касающееся машинного расчета траекторий ПМСВ. Так вблизи точки высвечивания зависимость волнового числа от поля подходит к своему крайнему значению весьма полого.
Такое обстоятельство
иллюстрируется рис.15, где показана схема формирования интервалов волновых
чисел при различных интервалах поля. Утолщенная сплошная линия – зависимость
волнового числа от поля, соответствующая закону дисперсии ПМСВ [20].
Вертикальными точечными линиями показаны границы интервала волновых чисел, соответствующих
интервалу полей при заданной частоте. Пунктирными линиями показаны границы
интервалов полей на одном шаге и соответствующие им границы интервалов волновых
чисел. Интервалы полей различаются тем, что один из них ![]() расположен
вблизи нижней полевой границы зависимости волнового числа от поля, а другой
расположен
вблизи нижней полевой границы зависимости волнового числа от поля, а другой ![]() – вблизи верхней.
– вблизи верхней.
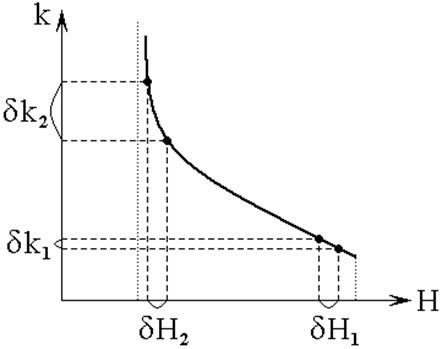
Рис.15. Схема формирования интервалов волновых чисел при различных интервалах поля.
Из рисунка видно, что при
равных по длине интервалах поля ![]() , интервалы значений
волновых чисел, соответствующих тем же интервалам поля, значительно различаются,
то есть
, интервалы значений
волновых чисел, соответствующих тем же интервалам поля, значительно различаются,
то есть ![]() . Таким образом, если шаг по
. Таким образом, если шаг по ![]() при машинном интегрировании системы (10)-(12)
сохраняется неизменным, что в первом приближении можно считать соответствующим
неизменности интервала поля
при машинном интегрировании системы (10)-(12)
сохраняется неизменным, что в первом приближении можно считать соответствующим
неизменности интервала поля ![]() при каждом шаге, то
интервал изменения волнового числа при уменьшении поля на каждом шаге
увеличивается.
при каждом шаге, то
интервал изменения волнового числа при уменьшении поля на каждом шаге
увеличивается.
Поэтому при машинном интегрировании системы (10)-(12) изменение волнового числа на каждом шаге составляет тем большую величину, чем ближе поле приближается к своему нижнему пределу. Такой рост изменения волнового числа соответствует снижению точности машинного расчета, то есть эта точность вблизи нижней границы поля падает.
Однако поскольку, как установлено выше, высвечивание траектории ПМСВ соответствует приближению поля именно к такому пределу, то точность машинного расчета в области высвечивания также падает. Уменьшение шага расчета, на первых порах приводящее к улучшению результатов, также не дает желаемого эффекта, так как приводит к увеличению общего числа шагов, что порождает накопление ошибки расчета и увеличение его времени.
В настоящей работе при принятых
выше параметрах задачи оптимальным значением шага было принято ![]() , что обеспечивало для наиболее длинных
траекторий длиной до
, что обеспечивало для наиболее длинных
траекторий длиной до ![]() время счета не более 1-2 минут.
При увеличении длины шага на порядок нарушалась повторяемость траектории уже
начиная с
время счета не более 1-2 минут.
При увеличении длины шага на порядок нарушалась повторяемость траектории уже
начиная с ![]() . При уменьшении длины шага также на
порядок, время расчета увеличивалось до 10-20 минут, а накопление ошибки приводило
к ухудшению формы траекторий, особенно на расстоянии порядка
. При уменьшении длины шага также на
порядок, время расчета увеличивалось до 10-20 минут, а накопление ошибки приводило
к ухудшению формы траекторий, особенно на расстоянии порядка ![]() от их окончания, искажая картину
высвечивания. При этом в обоих случаях факт высвечивания сохранялся, однако
координата высвечивания
от их окончания, искажая картину
высвечивания. При этом в обоих случаях факт высвечивания сохранялся, однако
координата высвечивания ![]() смещалась, как
правило, в меньшую сторону на величину до
смещалась, как
правило, в меньшую сторону на величину до ![]() .
.
16. Рекомендации для эксперимента
Основным предметом проведенного рассмотрения является в первую очередь демонстрация возможного решения варианта математической задачи, сходной с задачей о биллиардах [1], на основе конкретного вида закона дисперсии (3) и изменения волноведущей среды (13)-(14).
Однако, поскольку математическая часть задачи базируется на основе картины распространения магнитостатических волн в неоднородно намагниченной пластине феррита, следует рассмотреть возможности экспериментального наблюдения описанных явлений.
Прежде всего отметим, что распространение
ПМСВ в поле типа «вала» в экспериментах на пленках железоиттриевого граната
наблюдалось в ряде работ [9-11]. Был четко выявлен близкий к синусоидальному
вид траекторий волновых пучков шириной до ![]() , распространявшихся
на расстояние до
, распространявшихся
на расстояние до ![]() . Четко регистрировались до двух
периодов траекторий, после чего затухание волны достигало 40-50 дБ, что находилось
на грани чувствительности использованной аппаратуры.
. Четко регистрировались до двух
периодов траекторий, после чего затухание волны достигало 40-50 дБ, что находилось
на грани чувствительности использованной аппаратуры.
Таким образом, если полагать четко выраженными два периода траекторий, то для наблюдения стохастичности следует выбирать условия эксперимента так, чтобы хаотизация траекторий проявлялась уже на этом расстоянии.
Из приведенного выше
рис.13
можно видеть, что наиболее резко скачкообразный характер траекторий проявляется
вблизи верхней границы спектра ПМСВ. Таким образом, надо работать именно в этой
области частот, ниже верхней границы не более чем на ![]() .
При этом волновое число будет составлять порядка
.
При этом волновое число будет составлять порядка ![]() , что
соответствует длине волны
, что
соответствует длине волны ![]() . Если ПМСВ будут
возбуждаться проволочной антенной, то ее диаметр должен быть не более чем того
же порядка.
. Если ПМСВ будут
возбуждаться проволочной антенной, то ее диаметр должен быть не более чем того
же порядка.
В работах [9-11] использовались
антенны с диаметром проводника порядка ![]() , что
позволяло достаточно эффективно возбуждать ПМСВ длиной до
, что
позволяло достаточно эффективно возбуждать ПМСВ длиной до ![]() . Таким образом, наблюдение стохастизации
ПМСВ с такими возбудителями можно считать весьма реальным. Однако, все же,
по-видимому, более предпочтительно использовать микрополосковую технику, где
размер центрального проводника полосковой линии при использовании фотолитографии
может быть уменьшен до
. Таким образом, наблюдение стохастизации
ПМСВ с такими возбудителями можно считать весьма реальным. Однако, все же,
по-видимому, более предпочтительно использовать микрополосковую технику, где
размер центрального проводника полосковой линии при использовании фотолитографии
может быть уменьшен до ![]() .
.
Заметим дополнительно, что факт
бесконечного увеличения волнового числа вблизи границы существования ПМСВ также
не является бесспорным. Так в работах [28-30] показано, что при учете затухания
ПМСВ допустимое волновое число по величине сверху ограничивается. Так при
принятом в работе [30] значении параметра затухания ![]() ,
максимальное значение действительной части волнового числа составляет около
,
максимальное значение действительной части волнового числа составляет около ![]() .
.
Таким образом, отмеченная здесь расходимость (уход на бесконечность) волнового числа в точке высвечивания является идеализацией, обусловленной отсутствием затухания ПМСВ и в реальных условиях должна быть ограничена предельным значением, определяемым диссипативными свойствами среды.
Из этого следует вывод, что в
качестве волноведущей среды следует выбирать пленки с как можно меньшим
затуханием. Так в случае параметра затухания типичного для монокристалла железоиттриевого
граната ![]() (что соответствует ширине линии
(что соответствует ширине линии ![]() ), максимальное значение волнового числа
увеличивается примерно на порядок, что как раз соответствует величине,
требуемой для эксперимента.
), максимальное значение волнового числа
увеличивается примерно на порядок, что как раз соответствует величине,
требуемой для эксперимента.
Итак, можно сделать вывод, что
для экспериментального наблюдения стохастизации траекторий ПМСВ необходимо
использовать пленки железоиттриевого граната с параметром затухания не более ![]() , микрополосковые преобразователи с
шириной полоска не более
, микрополосковые преобразователи с
шириной полоска не более ![]() и работать на частотах,
ниже верхней границы спектра ПМСВ не более чем на
и работать на частотах,
ниже верхней границы спектра ПМСВ не более чем на ![]() . Все
эти требования в реальных условиях вполне достижимы, что позволяет надеяться на
успешную реализацию эксперимента.
. Все
эти требования в реальных условиях вполне достижимы, что позволяет надеяться на
успешную реализацию эксперимента.
Заключение
Основные результаты работы сводятся к следующему.
Для ферритовой пластины со свободной поверхностью рассмотрен частный случай поля сложной формы – продольно неоднородного типа «вала» с периодической модуляцией высоты, крутизны склонов и сдвига вершины.
Показано, что в таком поле траектории ПМСВ становятся неустойчивыми и вместо псевдосинусоидального (типичного в отсутствие модуляции) характера приобретают стохастический, проявляющийся в хаотических скачках амплитуды, частоты и фазы, выраженный тем сильнее, чем глубже модуляция.
Построен фазовый портрет траекторий ПМСВ. Показано, что в отсутствие модуляции фазовая траектория описывает устойчивый цикл, форма которого близка к эллиптической. При наличии модуляции фазовый портрет размазывается, приобретая вид множества разного размера наложенных друг на друга неправильных четырехугольников с вогнутыми сторонами и острыми углами.
Выявлен эффект “высвечивания” траекторий, проявляющийся в их обрыве при попадании траектории в область пространства, где поле становится меньше соответствующего нижней границе спектра ПМСВ, что сопровождается значительным ростом волнового числа и в ряде случаев отклонением вектора фазовой скорости от нормали к направлению поля на величину, большую угла отсечки.
Исследована зависимость максимальной (до обрыва) длины траекторий ПМСВ от пространственной частоты модуляции поля. Обнаружен сильно изрезанный характер этой зависимости с четко выраженными минимумами, когда пространственный период псевдосинусоидальной траектории ПМСВ равен целому, особенно четному числу периодов модуляции.
Установлена, что стохастичность траектории выражена тем сильнее, чем меньше длина траектории до высвечивания, на основе чего в качестве меры стохастичности предложено использовать «длину высвечивания», связанную со степенью стохастичности обратной зависимостью.
Исследована зависимость длины высвечивания траекторий ПМСВ от коэффициента глубины модуляции при различных ее видах. Показано, что длина высвечивания минимальна при модуляции крутизны склонов «вала», принимает среднее значение при модуляции высоты вершины и становится максимальной при модуляции сдвига вершины «вала».
На основе анализа пространственной конфигурации траекторий и фазовых портретов ПМСВ в равных по полю условиях показано, что наиболее сильную хаотизацию траекторий вызывает модуляция крутизны склонов «вала», несколько меньшую – модуляция высоты вершины и самую меньшую – модуляция сдвига вершины, что находится в полном соответствии с критерием, полученным на основе длины высвечивания.
Исследованы условия стохастизации траекторий ПМСВ на различных частотах. Показано, что наиболее сильная стохастизация происходит при работе на частоте, близкой к верхней границе спектра ПМСВ, где волновое число достигает значительной величины.
Отмечена аналогия наблюдаемых явлений с движением частицы в «перемешивающем биллиарде», частным случаем которого является двумерный волноводный канал типа «стадиона». В качестве параметра, обеспечивающего упомянутое «перемешивание», указано волновое число ПМСВ, изменение которого при малом изменении поля может быть весьма большим, что приводит к потере памяти системы о начальных условиях.
Рассмотрена практическая реализация наблюдаемых явлений и даны рекомендации к их наблюдению в эксперименте, состоящие в использовании пленок железоиттриевого граната с малым параметром затухания, микрополосковых преобразователей с малой шириной полоска и работе в диапазоне частот вблизи верхней границы спектра ПМСВ.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику. М.: Наука. 1988.
2. Анищенко В.С., Нейман А.Б., Мосс Ф., Шиманский-Гайер Л. // УФН. 1999. Т.169. №1. С.7.
3. Моносов Я.А. Нелинейный ферромагнитный резонанс. М.: Наука. 1971.
4. Захаров В.Е., Львов В.С., Старобинец С.С. // УФН. 1974. Т.114. №4. С.609.
5. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.
6. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000. Т.42. № 6. С.1062.
7. Alvarez L.F., Pla O., Chubykalo O. // Phys.Rev.B. 2000. V.61. №17. P.11613.
8. Семенцов Д.И., Шутый А.М. // УФН. 2007. Т.177. № 8. С.831.
9. Vashkovsky A.V., Lock E.H., Shcheglov V.I., Zubkov V.I. // IEEE Trans. on Magn. 1990. V.26, P.480.
10. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1995. Т.40. №2. С.313.
11. Вашковский А.В., Зубков В.И., Щеглов В.И. // РЭ. 1996. Т.41. №12. С.1413.
12. Щеглов В.И. // Сб.тр. XVII межд. шк.-сем. “Новые магнитные материалы микроэлектроники”. М.: УРСС. 2000. С.331.
13. Зубков В.И., Щеглов В.И. // Письма в ЖТФ. 2001. Т.27. №8. С.90.
14. Щеглов В.И. // Сб. тр. XVIII Межд. шк.-сем. “Новые магнитные материалы микроэлектроники”. М.: Изд.МГУ. 2002. С.810.
15. Щеглов В.И. // Сб. тр. VII Межд. сем. "Магнитные фазовые переходы". Махачкала: Изд. Института физики Дагестанского научного центра РАН. 2005. С.62.
16. Щеглов В.И. // Сб. тр. VIII Межд. сем. "Магнитные фазовые переходы". Махачкала: Изд. Института физики Дагестанского научного центра РАН. 2007. С.67.
17. Щеглов В.И. // Сб. тр. VII Межд. сем. "Магнитные фазовые переходы". Махачкала: Изд. Института физики Дагестанского научного центра РАН. 2004. С.76..
18. Щеглов В.И. // Сб. тр. VII Межд. сем. "Магнитные фазовые переходы". Махачкала: Изд. Института физики Дагестанского научного центра РАН. 2005. С.66.
19. Щеглов В.И. // Сб. тр. XXI Межд. конф.«Электромагнитное поле и материалы». Москва: «НИУ МЭИ». 2013. С.231.
20. Damon R.W., Eshbach J.R. // J. Phys. Chem. Solids. 1961. V.19. №3/4. P.308.
21. Auld B.A. // Bell Syst.Tech.J. 1965. V.44. №3. P.495.
22. Беспятых Ю.И., Зубков В.И., Тарасенко В.В. // ЖТФ. 1980. Т.50. №1. С.140.
23. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.
24. Mandelbrot B.B. The fractal geometry of nature. S.F. 1982.
25. Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1989. Т.34. №7. С.1381.
26. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1991. Т.36. №10. С.1959.
27. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1991. Т.36. №12. С.2345.
28. Вызулин С.А., Розенсон А.Э., Шех С.А. // РЭ. 1991. Т.36. №1. С.164.
29. Вызулин С.А. Обобщенные плоские волны в задачах электродинамики магнитогиротропных сред. Диссертация. на соискание уч. ст. д.ф.-м.н. Краснодар. 2000.
30. Макаров П.А., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2014. №7. URL: http://jre.cplire.ru/jre/jul14/8/text.html, http://jre.cplire.ru/jre/jul14/8/text.pdf.