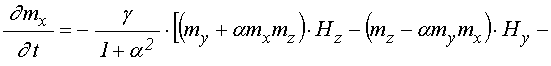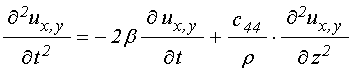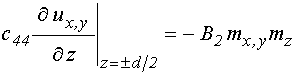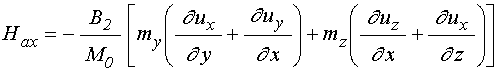"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 10, 2015

оглавление

УДК 537.874; 537.624

НЕЛИНЕЙНЫЕ ГИПЕРЗВУКОВЫЕ КОЛЕБАНИЯ МАГНИТОСТРИКЦИОННОГО ПРЕОБРАЗОВАТЕЛЯ НА ЧАСТОТАХ, КРАТНЫХ ЧАСТОТЕ ВОЗБУЖДЕНИЯ.

ЧАСТЬ 2. УМНОЖЕНИЕ ЧАСТОТЫ ВОЗБУЖДЕНИЯ

 

В. С. Власов 1, В. Г. Шавров 2, В. И. Щеглов 2

1 Сыктывкарский государственный университет

2 Институт радиотехники и электроники им. В.А.Котельникова РАН

Статья получена 20 сентября 2015 г.

 

Аннотация. Рассмотрены вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. В случае, когда резонансная частота упругой подсистемы превышает в кратное число раз резонансную частоту магнитной, в сильно нелинейном режиме возбуждения возможно умножение исходной частоты как в целочисленном, так и в дробном отношении. Рассмотрены случаи круговой и линейной поляризации возбуждающего поля. Выявлены различные варианты умножения и предложены гипотезы для их интерпретации.

Ключевые слова: магнитострикционный преобразователь, нелинейные колебания, умножение частоты.

Abstract. The forced vibrations of magnetization and elastic displacement in normal magnetized ferrite plate having magnetoelastic properties are investigated. In the case when resonance frequency of elastic system exceeds on the multiple part of resonance frequency of magnetic system, in strong nonlinear regime of excitation it is possible the multiplication of initial frequency in whole-number and also in fractional-number relation. It is investigated the cases of circular and linear polarization of excitation field. It is found the different regimes of multiplication and supposed some hypotheses of its interpretation.

Key words: magnetostriction transducer, nonlinear vibrations, multiplication of frequency.

 

Введение

Настоящая работа посвящена исследованию кратного преобразования частоты в схеме магнитострикционного преобразователя и является второй частью работы [1].   

В первой части [1] рассмотрены вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. Показано, что в случае, когда резонансная частота упругой подсистемы составляет кратную часть резонансной частоты магнитной, в сильно нелинейном режиме возбуждения возможно деление исходной частоты как в целочисленном, так и в дробном отношении. Рассмотрены случаи круговой и линейной поляризации возбуждающего поля. Выявлены различные режимы деления и предложены гипотезы для их интерпретации.

Настоящая работа, будучи продолжением [1], посвящена вопросу умножения исходной частоты возбуждения. Предварительное исследование умножения частоты в схеме магнитострикционного преобразователя выполнялось в работах [2-4], где были рассмотрены вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. Было показано, что в случае, когда резонансная частота упругой подсистемы в кратное число раз превышает резонансную частоту магнитной, в сильно нелинейном режиме возбуждения возможно умножение исходной частоты как в целочисленном, так и в дробном кратном отношении. Рассмотрено соотношение процесса умножения с временами релаксации магнитных и упругих колебаний. Показано, что устойчивое умножение наблюдается только в том случае, когда время релаксации упругих колебаний не менее чем на порядок превышает время релаксации магнитных. Отмечена высокая критичность процесса умножения к условиям релаксации, уровню возбуждения и степени нелинейности магнитных колебаний. Интерпретация умножения частоты выполнена на основе того же механизма ударного возбуждения, что для деления [1,5,6], с учетом соотношения периодов возбуждаемых колебаний и вынуждающего воздействия.

Однако выполненное в работах [2-4] рассмотрение является недостаточно полным. Так, не выявлено различия между ударным и непрерывным режимами возбуждения, сделан однозначный вывод о необходимости соответствия между временами релаксации магнитной и упругой систем и интервалом временем реализации умножения. Не отмечена роль величины константы магнитоупругого взаимодействия, имеющая в процессе деления, как показано в [1], в решающее значение.

Настоящая работа, являясь логическим продолжением [1], выполнена в том же ключе и, включая в себя часть результатов, полученных в [2-4], развивает и углубляет их с целью более полного описания явления умножения. По ходу изложения будет также проведена параллель с описанными в работе [1] явлениями деления.

1. Геометрия задачи и основные уравнения

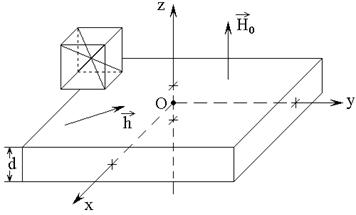
Геометрия задачи, совпадает с принятой в работе [1], а также в [2-6] и предшествующих работах [7-9]. Ее схема показана на рис.1. В основе лежит пластина толщины , обладающая магнитными, упругими и магнитоупругими свойствами. Материал пластины имеет кубическую кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью пластины.

 

Рис.1. Геометрия задачи. Слева – схема кристаллографической ячейки.

Внешнее постоянное магнитное поле  приложено перпендикулярно плоскости пластины, переменное магнитное поле  действует в плоскости пластины. Задача решается в декартовой системе координат , плоскость  которой совпадает с плоскостью пластины, а оси ,  и  параллельны ребрам куба кристаллографической ячейки. Центр системы координат  находится в центре пластины, так что ее плоскости соответствуют координатам .

Полная система уравнений и граничных условий, аналогичная приведенной в работе [1], имеет вид:

уравнения для компонент намагниченности :

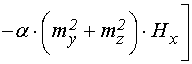                                            ;                             (1)

 

где  уравнения для  и  получаются циклической перестановкой , , ;

уравнения для компонент упругих смещений :

,                                         (2)

где  – плотность материала пластины;   

граничные условия:

.                                                     (3)

Входящие в уравнение (1) эффективные поля  имеют вид:

;                                                                                      (4)

;                                                                                     (5)

,                                                               (6)

где  – внешнее постоянное поле,  – компоненты внешнего переменного поля, а выражения для компонент полей  имеют вид:

,            (7)

при этом  и  получаются из (7) циклической перестановкой , , .

В дальнейшем будут рассмотрены два варианта поляризации переменного поля – круговая и линейная. При круговой поляризации правого направления вращения поля имеют вид:

,         ,                       (8)

причем при точной круговой поляризации полагается .

При линейной поляризации поля имеют вид:

,         ,                                                     (9)

что получается из формул (8) при .

Аналогично [1], система (1)-(3) была приведена к эквивалентной системе из семи уравнений первого порядка без граничных условий, которая решалась численно методом Рунге-Кутта четвертого порядка [10]. Результаты такого решения приведены далее.

2. Основные параметры задачи 

Основные параметры задачи совпадают с принятыми в работе [1]. Параметры материала пластины типичны для монокристалла железоиттриевого граната (ЖИГ): ; . Для более наглядного выявления излагаемых далее результатов значение константы магнитоупругого взаимодействия было взято в несколько раз большим:, где  – целое число от 2 до 40, а . Аналогично [1] параметры затухания магнитной и упругой подсистем были выбраны равными ,  . При этом время релаксации (то есть спада амплитуды свободных колебаний в  раз) для магнитных колебаний составляло около , а для упругих – около . Постоянное поле было равным , частота возбуждения, соответствующая частоте ферромагнитного резонанса (ФМР) в этом поле, равнялась . Резонансная толщина магнитной пластины на первой моде для этой частоты составляла .

Переменное поле прикладывалось в плоскости пластины и имело круговую или линейную поляризацию. Другие параметры, используемые для построения кривых, указаны в подписях к рисункам и в тексте. Развитие колебаний рассматривалось во временном интервале  с шагом .

Для осуществления умножения частоты система настраивалась таким образом, чтобы частота упругого резонанса пластины, определяемая ее толщиной, была в желаемом кратном отношении больше частоты ФМР, на которой производилось возбуждение. С этой целью толщина магнитной пластины выбиралась в кратное число раз меньше резонансной, то есть , где  – требуемая кратность. 

3. Два варианта процесса умножения частоты

Предварительное рассмотрение, аналогичное проделанному в работе [1], показало, что умножение частоты, как и деление, происходит принципиально различным образом, в зависимости от того, является ли поляризация возбуждающего поля круговой или линейной.

В случае круговой поляризации решающую роль играют процессы релаксации магнитных и упругих колебаний, поэтому для успешной реализации умножения частоты в этом случае важно соотношение между моментом включения возбуждения и временем наблюдения явления. 

В случае линейной поляризации подобная зависимость отсутствует, так что устойчивое умножение частоты наблюдается в любой момент времени, достаточно удаленный от момента включения возбуждения.

Такое различие между круговой и линейной поляризацией относительно процесса умножения частоты происходит из-за того, что при круговой поляризации возбуждающего поля прецессия намагниченности при любом его уровне всегда остается круговой и какие-либо высокочастотные гармоники в ее движении в первом приближении отсутствуют. То есть умножение частоты в установившемся режиме здесь в какой-то степени затруднено. 

В то же время, при линейной поляризации прецессия имеет эллиптический характер, тем более отличный от кругового, чем уровень возбуждения выше. Такое движение вектора намагниченности богато высокочастотными гармониками, поэтому умножение частоты становится вполне естественным.

Ввиду принципиального различия участвующих в этих процессах механизмов, рассмотрим их по отдельности, то есть сначала обратимся к случаю круговой поляризации типа (8), а затем – к линейной типа (9).

4. Круговая поляризация поля возбуждения. Общие положения

Случай круговой поляризации наиболее прост с точки зрения прецессии намагниченности, ибо как возбуждение, так и поле магнитоупругого взаимодействия за вычетом слабого влияния кубической анизотропии является симметричным относительно направления постоянного поля, так что прецессия намагниченности также является весьма близкой к круговой. Дополнительная проверка показывает, что при  принятых здесь параметрах задачи (раздел №2) вплоть до значений константы , близком к значению, соответствующему переориентации вектора намагниченности от нормали к плоскости пластины ( [11]), отклонение прецессии намагниченности от круговой не превышает единиц процентов и на результатах, описываемых далее, никак не сказывается.   

В силу кругового характера прецессии намагниченности, в установившемся режиме какие-либо условия для возбуждения высокочастотных гармоник отсутствуют. Поэтому решающую роль приобретают биения между частотами собственных колебаний упругой системы и переменного поля [12-14], имеющие место в начальный момент после включения возбуждения.

Механизмом, обеспечивающим биения в этом случае, является ударное возбуждение упругой  системы за счет кратковременного воздействия магнитной. То есть схема получения преобразованных частот при умножении аналогична таковой для случая деления [1]. Выбор той или иной кратности преобразованной частоты обеспечивается собственными резонансными условиями упругих колебаний пластины (ее первой моды), определяемыми ее толщиной. 

При условии превышения времени релаксации упругой системы над уровнем релаксации магнитной, такие биения продолжаются вплоть до завершения процесса упругой релаксации, то есть до установления стационарного режима вынужденных колебаний. Таким образом именно здесь, то есть в промежуток времени между временами релаксации магнитной и упругой систем следует ожидать проявления эффекта умножения частоты возбуждающего поля. 

5. Умножение частоты на два

Как и в работе [1] в качестве наиболее простого примера рассмотрим сначала случай умножения частоты на два, для чего выберем толщину магнитной пластины вдвое меньше той, которая соответствует резонансу на частоте возбуждения. При этом собственной резонансной частотой упругих колебаний будет удвоенная частота переменного поля. 

Так частоте возбуждения  соответствует упругий резонанс пластины толщиной . Получаемой в результате умножения частоте  соответствует упругий резонанс пластины, толщиной вдвое меньшей: .

Будем рассматривать два режима возбуждения: линейный при  и сильно нелинейный – при  (напомним, что, согласно [8,9], переход от линейного к нелинейному режиму соответствует ). Константу магнитоупругого взаимодействия положим равной: .

6. Значительный промежуток времени  

Как отмечено в работе [1], для эффективного проявления механизма ударного возбуждения необходим достаточный уровень переменного поля. Однако хотя там такое обстоятельство отмечено, но роль его на достаточном промежутке времени, сравнимом со временем упругой релаксации, не выявлена. Для ликвидации этого пробела обратимся к рассмотрению, иллюстрируемому рис.2, где показаны развертки во времени магнитных и упругих колебаний при двойной и половинной толщине пластины в промежутке времени от нуля до , сравнимом со временем релаксации упругой системы.

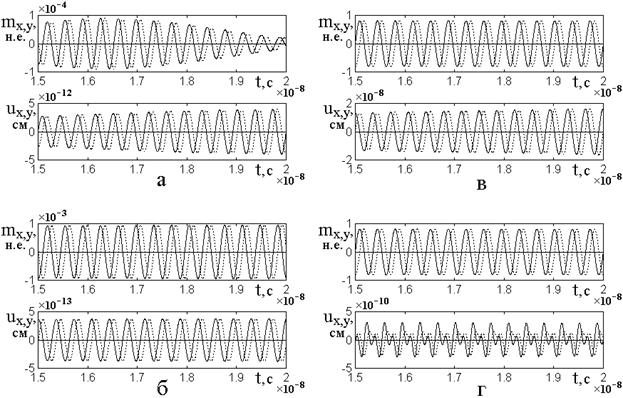
Рис.2а соответствует чисто линейному возбуждению системы, обе части которой, магнитная и упругая, настроены в резонанс с частотой переменного поля. 

Видно, что здесь происходит периодическая перекачка энергии из магнитной системы в упругую и обратно, причем время одного полного цикла перекачки составляет около . Это время примерно вдвое меньше времени релаксации магнитной системы (), то есть близко ко времени ударного возбуждения упругой системы при стовосьмидесятиградусном  перемагничивании магнитной пластины со сходными параметрами [15-18].

 

Рис.2. Развертки во времени магнитных (верхние эпюры) и упругих (нижние эпюры) колебаний при различных уровнях возбуждения и коэффициентах кратности преобразования.

Компоненты  и  тех и других колебаний, будучи сдвинутыми по фазе относительно друг друга на , имеют одинаковую амплитуду, поэтому на рисунке сливаются и отдельно не выделены.

Константа магнитоупругого взаимодействия: .

Кратность преобразования частоты:

а,г – резонансный режим (толщина пластины: );

б,д – умножение на два (толщина пластины: );

в,е – деление на два (толщина пластины: ).

Амплитуда переменного поля:

а,б,в – ;   г,д,е – 

 

Полное установление амплитуды тех и других колебаний наступает при времени порядка , что более чем вдвое не достигает времени  релаксации упругой системы (). Столь быстрое установление, по-видимому, происходит из-за того, что вследствие сильной связи, обеспечиваемой резонансными условиями, магнитная релаксация вносит значительный вклад в релаксацию упругую, приводя к более быстрому затуханию свободной составляющей упругих колебаний.  

Замечание. Сходный вопрос формирования затухания одной из связанных систем за счет затухания другой рассмотрен в работах [19-23], хотя там установлено формирование магнитного затухания за счет упругого, в том числе в условиях резонанса [20-23]. С другой стороны, в работе [24] отмечено, что в отсутствие резонанса условия для такого формирования отсутствуют. Здесь (рис.2а) наблюдается формирование упругого затухания за счет магнитного, то есть процесс обратный, описание которого в известной авторам литературе отсутствует, так что, по-видимому, может составить предмет самостоятельного исследования, за рамки настоящей работы однако выходящего.  

В установившемся режиме, то есть при времени больше , амплитуда магнитных колебаний составляет , а амплитуда упругих – .

Рис.2б соответствует также линейному возбуждению системы, причем хотя магнитная часть системы остается настроенной в резонанс, но собственная частота колебаний упругой системы вдвое выше частоты возбуждения (толщина пластины настроена на умножение). Как следствие выхода упругих колебаний из условий резонанса, нагружение магнитной системы упругой становится значительно меньше, чем в предыдущем случае, то есть магнитные колебания освобождаются от нагрузки упругими и их амплитуда в установившемся режиме значительно (примерно в  раз) возрастает, достигая  Амплитуда же упругих колебаний, вследствие выхода из резонанса, наоборот падает до , то есть примерно в  раз.

Время установления магнитных колебаний теперь определяется в подавляющей степени именно магнитной релаксацией и составляет около . Поскольку здесь упругие колебания не имеют собственной свободы (ударное возбуждение отсутствует вследствие плавности нарастания магнитных колебаний), а управляются практически полностью магнитными колебаниями, время их установления также равняется времени установления магнитных и составляет те же .

Рис.2в соответствует также линейному возбуждению системы, причем магнитная часть системы по-прежнему остается настроенной в резонанс, но собственная частота колебаний упругой системы теперь устанавливается вдвое ниже частоты возбуждения (толщина пластины настроена на деление).

Здесь также резонансные условия сохраняются лишь для магнитной системы, а для упругой – отсутствуют, поэтому упругая система нагружает магнитную в весьма малой степени. Относительно магнитных колебаний этот случай практически ничем не отличается от предыдущего: время установления – , амплитуда в установившемся режиме –  Относительно упругих единственное отличие состоит лишь в увеличении амплитуды в установившемся режиме до  (то есть примерно в  раза), что, по-видимому, обусловлено четырехкратным увеличением толщины пластины по сравнению со случаем рис.2б, что можно трактовать как следствие такого же увеличения энергии, передаваемой переменным полем магнитной системе из-за увеличения ее  объема или просто как увеличение относительного удлинения поперечного размера пластины из-за абсолютного увеличения ее толщины. 

Рис.2г соответствует сильно нелинейному возбуждению системы, обе части которой, магнитная и упругая, настроены в резонанс с частотой переменного поля. 

Видно, что в этом случае амплитуда магнитных колебаний, начинаясь практически с единицы, за время около  устанавливается на уровне около  Это время как раз соответствует ударному возбуждении упругой системы (аналогично рис.2а), после чего ударный характер процесса заканчивается и дальнейшая передача энергии от магнитной системы к упругой происходит плавно с постоянной времени, определяемой резонансным возбуждением упругой системы. То есть, упругая система, будучи резонансной, не позволяет развиться своим колебаниям мгновенно, а допускает увеличение амплитуды только с постоянной времени, определяемой собственным временем упругой релаксации. При этом установление колебаний упругой системы происходит за время, несколько большее , то есть находится за правым краем рисунка. Дополнительное исследование показывает, что практически полное установление происходит при времени порядка

В установившемся режиме амплитуда магнитных колебаний составляет около , а амплитуда упругих – около .

Рис.2д соответствует сильно нелинейному возбуждению системы, причем хотя магнитная часть системы остается настроенной в резонанс, но собственная частота колебаний упругой системы вдвое выше частоты возбуждения (толщина пластины настроена на умножение). Развитие во времени магнитных колебаний здесь практически не отличается от случая, представленного на рис.2г. Это сходство обусловлено весьма сильным уровнем возбуждения, так что магнитная система, хотя и освобождается от нагружения упругой, но не может развить своих колебаний выше , так как вектор намагниченности и так уже прецессирует почти в плоскости пластины (отклоняется менее чем на ) и дальше отклоняться от нормали ему просто некуда.

Развитие упругих колебаний происходит ударным образом в промежуток времени до , после чего они плавно релаксируют с постоянной, соответствующей времени релаксации упругой системы. Установление происходит при времени около  на уровне , то есть ниже резонансного случая (рис.2д) примерно в  раз. 

Рис.2е соответствует сильно нелинейному возбуждению системы, причем хотя магнитная часть системы остается настроенной в резонанс, но собственная частота колебаний упругой системы вдвое ниже частоты возбуждения (толщина пластины настроена на деление). Развитие магнитных колебаний здесь опять ничем не отличается от показанного на рис.2г и 2д и обусловлено теми же причинами. Развитие упругих колебаний здесь также происходит ударным образом за время , после чего они плавно релаксируют с постоянной, соответствующей времени релаксации упругой системы. Установление амплитуды происходит при времени около  на уровне , то есть ниже резонансного случая (рис.2д) примерно в  раз. 

Отметим, что здесь, в отличие от случая линейного возбуждения (рис.2б и 2в), при переходе от умножения к делению амплитуда установившихся колебаний не увеличивается, а уменьшается, примерно в  раз. Возможной причиной такого уменьшения может явиться тот факт, что при сильно нелинейном возбуждении резонансная кривая ФМР значительно деформируется, наклоняясь в сторону высоких частот [25-27], то есть удаляясь от резонансной частоты упругих колебаний, так что условия передачи энергии от магнитной системы к упругой заметно ухудшаются, что и приводит к уменьшению амплитуды упругих колебаний.

7. Малый промежуток времени

Рассмотрим теперь роль нелинейности колебательной системы при  большой амплитуде возбуждения на малом промежутке времени, что позволит выявить тонкую структуру колебаний основной и удвоенной частоты. Выберем интервал времени между  и , который находится как раз между временами релаксации магнитной и упругой систем, ближе к релаксации магнитной.

Обратимся к рис.3, где показаны развертки во времени магнитных и упругих колебаний при различной толщине пластины и уровне возбуждения.

 

Рис.3. Развертки во времени магнитных и упругих колебаний в пластине при различной толщине и уровне возбуждения.

Сплошные линии – -компоненты, пунктирные линии – -компоненты.

а – , ;  б – ,  ;

в – , ; г – , .

 

Рис.3а и 3б соответствуют линейному возбуждению при малой амплитуде, причем на рис.3а обе системы, магнитная и упругая, настроены в резонанс с частотой возбуждения, тогда как на рис.3б в резонансе находится только магнитная система, а упругая настроена на двойную частоту.

Видно, что в обоих случаях в компонентах как магнитной, так и упругой составляющей присутствия двойной частоты не наблюдается. Соотношение амплитуд тех и других колебаний подробно разобрано при рассмотрении рис.2а,б, поэтому здесь не обсуждается. 

Рис.3в и 3г соответствуют нелинейному возбуждению при большой амплитуде переменного поля, причем на рис.3в обе системы настроены в резонанс с полем, тогда как на рис.3г магнитная система остается в резонансе, а упругая настроена на двойную частоту.

Видно, что в случае обоих резонансов (рис.3в) двойная частота, несмотря на высокий уровень возбуждения, полностью отсутствует, что происходит из-за кругового характера прецессии. Однако в случае настройки упругого резонатора на двойную частоту (рис.3г) в упругих колебаниях (нижняя эпюра), хотя и преобладает основная составляющая, тем не менее появляется заметная составляющая удвоенной частоты. По компоненте  ее амплитуда составляет около от амплитуды на основной частоте, а по компоненте  – около .

Замечание. Можно полагать, что наблюдаемое на рис.3г различие амплитуд компонент  и  с магнитной и кристаллографической  анизотропией ЖИГ не связано, так как плотность энергии системы в целом (работа [1], формула (3)), относительно компонент намагниченности и смещения является изотропной. С другой стороны, упомянутое различие может быть связано с участием релаксации упругих колебаний. Так, дополнительная проверка на достаточно большом промежутке времени показывает, что оно не является во времени постоянным, а по мере развития колебаний постепенно меняется на обратное с постоянной времени сравнимой со временем релаксации упругой системы. Вообще говоря, этот вопрос требует отдельного исследования, за рамки настоящей работы выходящего.  

Таким образом, можно видеть, что для реализации эффекта умножения частоты необходимыми условиями являются: соответствие толщины пластины резонансу на частоте, получаемой в результате умножения, а также достаточно высокий уровень возбуждения обеспечивающий сильное проявление нелинейности системы.

Используемое здесь понятие «сильной» нелинейности трактуется таким же образом, как сходное понятие в работе [1]. То есть при принятых здесь параметрах задачи (раздел №2) для заметной реализации эффекта умножения, то есть когда амплитуда второй гармоники – не менее  от амплитуды основной составляющей, необходим уровень возбуждения  более или порядка . Относительно намагниченности ЖИГ () это составляет около  раз, а относительно подмагничивающего поля () –  меньше почти на порядок.  

Как и в случае деления частоты [1], для такого уровня возбуждения резкий порог отсутствует, то есть удвоение реализуется по мере увеличения возбуждения достаточно плавно. 

Возвращаясь к данным, представленным на рис.3, отметим, что дополнительным условием успешной реализации умножения частоты является довольно критичный выбор интервала времени наблюдения относительно начала возбуждения, более подробно рассмотренный в следующем разделе.

8. Роль интервала времени

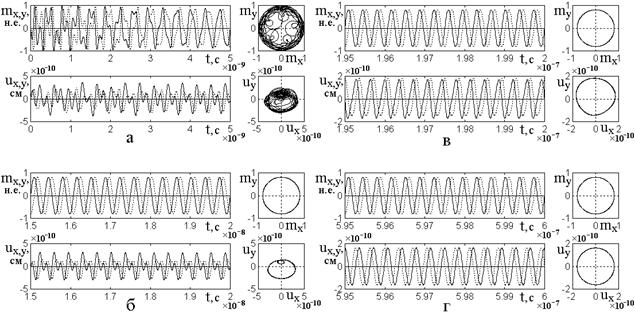
В разделе №3 отмечено, что характер процесса умножения частоты проявляется по разному в зависимости от начального момента возбуждения. Поэтому, аналогично работе [1],  выделим несколько характерных интервалов времени одинаковой протяженности, приходящихся на разные моменты относительно начала возбуждения. Соответствующее развитие колебаний во времени и отвечающие ему параметрические портреты иллюстрируются рис.4.

 

 

Рис.4. Развертки во времени магнитных и упругих колебаний, а также их параметрические портреты в различные промежутки времени от начала возбуждения. Умножение частоты на два.

Сплошные линии – -компоненты, пунктирные линии – -компоненты. Параметры: ,  .

а – ;    б – ;

в – ;   г – .

 

Из рис.4а видно, что сразу после включения возбуждения до времени порядка  магнитные колебания носят в какой-то степени беспорядочный характер, после чего до времени , соответствующего концу исследуемого интервала, частично стабилизируются. При этом выделенная частота, соответствующая частоте возбуждения, во всем интервале сохраняется. Однако упругие колебания практически сразу после начала интервала и до его конца сохраняют сильную примесь двойной частоты, что свидетельствует об интенсивном протекании процесса умножения.

Здесь проявление умножения подобно проявлению деления [1] и, надо полагать, обусловлено той же причиной – ударным возбуждением упругой системы за счет магнитной. Некоторое несовершенство получаемых колебаний до времени , как и при делении, соответствует влиянию магнитной системы и по прошествии времени ее релаксации прекращается.

Параметрический портрет для магнитных колебаний имеет вид широкого круглого кольца со множеством «завитков» внутри своей огибающей, что подобно случаю деления. Портрет же для упругих колебаний резко отличен и имеет вид сильно замазанного кольца с формой, заметно отличающейся от круговой периферийными искажениями. Такое отличие от довольно близкого к правильному круговому портрету при делении (нижняя правая эпюра на рис.3а в работе [1]), обусловлено тем обстоятельством, что при делении половинная частота выделяется практически в чистом виде (нижняя левая эпюра на рис.3а в работе [1]), тогда как здесь при умножении двойная частота в развертке во времени (левая нижняя эпюра на рис.4а) присутствует лишь в виде сильной примеси (около  по амплитуде) к основной частоте возбуждения. То есть в исследуемом интервале времени реализация процесса умножения, хотя имеет место, но более затруднена, чем реализация процесса деления.

Интервал времени , рассмотренный на рис.4б, находится примерно посередине между временами релаксации магнитных и упругих колебаний.

Видно, что здесь магнитные колебания носят чисто синусоидальный характер, синхронный с полем возбуждения. Соответствующий параметрический портрет имеет вид правильного узкого кругового кольца, отвечающего чисто вынужденным колебаниям. Упругие колебания, в отличие от предыдущего рисунка, имеют правильный регулярный характер, представляющий собой сочетания колебаний на основной частоте со значительной (около  по амплитуде) примесью частоты двойной. Параметрический портрет имеет вид узкого почти правильного кольца с единственным характерными завитком, соответствующим удвоенной частоте.

Таким образом, здесь процесс умножения происходит вполне упорядоченным образом, однако опять двойная частота проявляется на значительном фоне основной.

Следует отметить, что наблюдаемый здесь регулярный характер колебаний обусловлен тем, что выбранный интервал времени находится достаточно далеко от окончаний релаксации как магнитных, так и упругих колебаний. То есть здесь собственные магнитные колебания уже полностью затухли, а упругие еще пребывают в состоянии, далеком от окончательного затухания, так что на протяжении исследуемого интервала уменьшение их амплитуды в пределах рисунка настолько мало, что на глаз не заметно.

Интервал времени , рассмотренный на рис.4в характерен тем, что свободные магнитные колебания уже достаточно давно затухли, тогда как упругие хотя еще и сохраняют некоторую весьма малую амплитуду, однако совершенно недостаточную для проявления процесса умножения в явном виде. Следы умножения проявляются лишь в легком отклонении формы параметрического портрета упругих колебаний от точно круговой. Так можно заметить, что геометрический центр кольца на рисунке несколько смещен вверх (на ) и налево (на ) от точки пересечения осей координат. То есть здесь, в отличие от случая деления, процесс умножения частоты почти не заметен.

В интервале времени , рассматриваемом на рис.4г, все собственные колебания как магнитной, так и упругой систем полностью затухли, поэтому те и другие колебания имеют вид правильных синусоид с отсутствием каких-либо следов биений. Тот и другой параметрические портреты имеют вид правильных узких колец чисто круговой формы, что свидетельствует об установлении стационарного режима чисто вынужденных колебаний. 

Таким образом, с точки зрения реализации умножения частоты при круговой поляризации возбуждения наиболее благоприятным является интервал времени, промежуточный между временами релаксации магнитных и упругих колебаний, иллюстрируемый рис.4б.  

9. Умножение с целочисленной кратностью

Рассмотрим теперь другие возможности умножения частоты, для чего обратимся к рис.5. Здесь показаны варианты умножения частоты возбуждения на целое число, для чего толщина пластины выбиралась в целое число раз меньше резонансной, соответствующей частоте ФМР, то есть , где  – требуемая кратность умножения. Рис.5а соответствует кратности равной двум, 5б – трем, 5в – четырем, 5г – пяти и 5д – шести, 5е – семи. В качестве интервала для наблюдения выбран наиболее благоприятный: . Предварительная проверка показала, что во всех рассмотренных далее случаях в этом интервале колебания намагниченности остаются близкими к синусоидальным без заметной примеси умноженной частоты (как на рис.4б), поэтому внимание уделено только колебаниям упругого смещения.

Из рисунка видно, что во всех случаях колебания умноженной частоты налагаются на колебания основной, причем составляют от исчезающе малой величины при  (б) до почти  при  (д). При этом примесь умноженной частоты к основной по мере увеличения кратности испытывает почти периодические колебания. Так при  (а) она составляет около , при  (б) уменьшается до единиц процентов, при  (в) опять увеличивается до , при  (г) падает до , при   (д) возрастает почти до , после чего при  (е) снова падает до . Можно полагать, что в этом диапазоне кратностей (от  до ) умножение с четной кратностью более эффективно, чем с нечетной. Однако дополнительная проверка показывает, что при дальнейшем увеличении кратности примесь умноженной частоты падает уже только монотонно и при   составляет менее .  

 

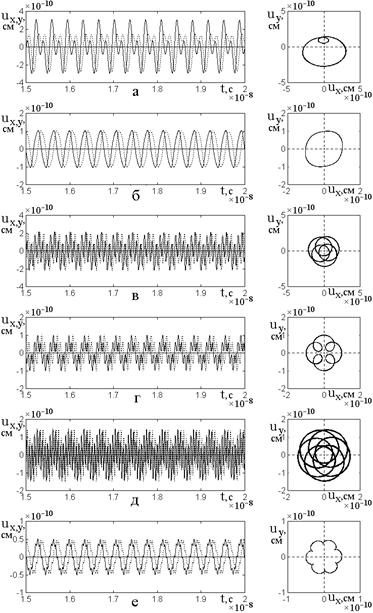
Рис.5. Развертки во времени для компонент упругого смещения и соответствующие им параметрические портреты при различной кратности целочисленного умножения частоты.

Сплошные линии – компоненты , пунктирные линии – компоненты .

Толщина пластины:  а – ;  б – ;  в – ;  г – ;  д – ;  е – .  Переменное поле: .

 

 Параметрические портреты отражают такое поведение умноженной частоты. Так при  (а) и  (б) портреты несколько несимметричны: центр портрета при  (а) смещен слегка вверх, причем в верхней части кольца присутствует завиток, тогда как при  (б) центр портрета остается на месте, однако сам портрет несколько вытягивается в направлении от первой к третьей координатной четверти. При больших, чем  значениях кратности, портреты относительно начала координат полностью симметричны и все содержат по нескольку завитков, число которых на единицу меньше величины кратности. При этом диаметры завитков на портретах при  (в) и  (д) превышают радиус основного кольца, так что они охватывают центр координат, тогда как диаметры завитков на портретах при  (г) и  (е) меньше основного радиуса, в результате чего завитки цента не охватывают. То есть можно видеть, что при четной кратности охват центра имеет место, а при нечетной –  отсутствует, что полностью коррелирует с величиной примеси умноженной частоты к исходной, наблюдаемой на соответствующих развертках во времени (левый столбец эпюр).      

При увеличении кратности более  завитки на параметрических портретах постепенно сглаживаются, в результате чего форма портрета постепенно приближается к правильному круговому кольцу.

10. Умножение с дробной кратностью

Рассмотрим теперь умножение частоты с дробной кратностью. Сразу отметим, что здесь картина заметно сложнее, чем при целочисленной кратности. Так при отклонении от целого числа уже на единицы процентов, хотя колебания намагниченности по-прежнему сохраняют практически синусоидальный характер, но колебания упругого смещения заметно меняются. Развертки во времени, в основном, меняются мало, однако параметрические портреты претерпевают серьезные изменения. 

Высокая сложность трансформации параметрического портрета при дробном делении частоты не позволяет простыми средствами построить адекватную модель явления, поэтому на данном этапе ограничимся лишь описанием его общей картины, стараясь выделить какие-то наиболее общие свойства.

В качестве первого общего правила можно отметить, что при отклонении кратности от целого числа количество внутренних завитков на параметрических портретах значительно увеличивается.

Рассмотрим несколько типичных вариантов изменения параметрического портрета при отклонении кратности умножения  от целочисленного значения. 

Обратимся к рис.6, где показаны параметрические портреты для компонент упругого смещения  при различной кратности  дробного умножения частоты. Выбраны два характерных интервала изменения кратности: первый между  и  (левые два столбца), второй между  и  (правые два столбца). Такой выбор обусловлен как максимальным наблюдаемым разнообразием изменения портретов, так и их принципиальным различием.

Из рассмотрения рис.6 можно выделить следующие особенности. Портреты, кратность которых равна целому числу, умноженному на , то есть имеющие , , , ,  имеют более редкий характер образующих линий, то есть более упорядочены. Остальные портреты значительно более сильно замазаны совокупностью внутренних лепестков. Такое обстоятельство наводит на мысль о важности соотношения периодов основной и умноженной частот. То есть, когда это соотношение выражается сравнительно небольшими целыми или полуцелыми числами, портрет более упорядочен, так как взаимное наложение одной частоты на другую повторяется периодическим образом. Когда же соотношение дробно или иррационально, портрет сильно замазывается, так как наложение частот друг на друга происходит несинхронно и повторение, если и происходит, то за весьма большие промежутки времени.  

 

 

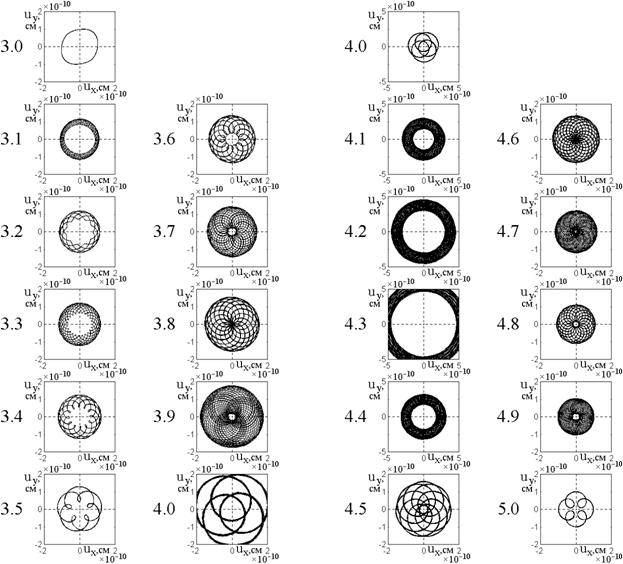
Рис.6. Параметрические портреты для компонент упругого смещения при различной кратности дробного умножения частоты.

Цифры слева от эпюр – соответствующие коэффициенты кратности . При этом толщина пластины равна , где .

 

По мере увеличения кратности внешний диаметр портрета от  при  увеличивается монотонно до  при , после чего при  сразу падает до ,  а затем уже монотонно уменьшается до  при . Внутренний диаметр  от , где он близок к , уменьшается до нуля при , после чего растет до  при , затем опять падает до нуля при , после чего снова начинает увеличиваться до конца исследуемого диапазона, где при  он составляет всего .

Такое взаимное изменение диаметров портрета отражает изменение величины примеси умноженной частоты к основной. Так при прохождении внутреннего диаметра через нуль характер внутренних завитков портрета меняется. До  они центра портрета не охватывают, то есть амплитуда умноженной частоты составляет менее от основной. После этого значения охват центра имеет место вплоть до , где амплитуда умноженной частоты достигает от основной. Далее при  охват пропадает, то есть амплитуда переваливает вниз через , после чего монотонно уменьшается, не превышая  при .

Замечание. Можно полагать, что наблюдаемый здесь максимум примеси умноженной частоты к основной при кратности  определяется соотношением времен релаксации магнитной и упругой систем, а также уровнем возбуждения. Это вопрос требует более подробного исследования, за рамки настоящей работы выходящего. 

11. Общая эффективность умножения при круговой поляризации

Таким образом, из проделанного рассмотрения можно сделать вывод, что умножение частоты упругих колебаний возможно при кратности умножения в интервале от  до , определяемой толщиной пластины, составляющей соответствующую часть от резонансной. Однако в отличие от случая деления, умноженная частота не выделяется в чистом виде, а всегда присутствует в качестве дополнительной примеси к основной частоте, причем величина примеси может составлять по амплитуде до  . При этом умножение с целочисленной кратностью наиболее эффективно в диапазоне кратности от  до , причем максимально при кратности равной , где амплитуда умноженной частоты составляет около  от амплитуды основной. Умножение с дробной кратностью имеет место во всем том же диапазоне, причем наиболее эффективно при кратности равной , где амплитуда умноженной частоты составляет около  от амплитуды основной. Выше и ниже упомянутого диапазона, во всем возможном интервале существования, амплитуда умноженной частоты не превышает  от амплитуды основной.

Замечание. Следует отметить, что в работе [2] в качестве необходимого условия реализации процесса умножения представлена линейность поляризации поля возбуждения. Однако, как следует из изложенного выше (разделы №10-11), умножение при круговой поляризации также возможно, хотя и требует для своего осуществления более сложных условий, причем колебания умноженной частоты самостоятельными не являются, а накладываются на колебания основной частоты, составляя по амплитуде до .    

12. Оптимальное соотношение времен релаксации и гипотеза ударного возбуждения 

Из проведенного рассмотрения (раздел №8)  следует, что умножение частоты при круговой поляризации возбуждения возможно только в интервале времени между временами релаксации магнитной и упругой систем. Такой вывод полностью совпадает с аналогичным выводом для процесса деления [1], так что и оптимальное соотношение времен релаксации здесь получается таким же. То есть умножение происходит тогда, когда релаксация магнитной системы уже завершилась, а упругой – еще продолжается. После окончания релаксации упругой системы процесс умножения также прекращается.

Оптимальные реализованные в настоящей работе условия наблюдения эффекта умножения частоты в материале, подобном ЖИГ, сводятся к тем же, что и для процесса деления [1]: ;  ;  ;  ;  ;  .

Как и в случае деления [1], основным фактором, обеспечивающим реализацию процесса умножения частоты является ударное возбуждение упругой системы в течение промежутка времени, когда колебания магнитной системы являются достаточно эффективными. Время такого ударного возбуждения, то есть как бы продолжительность «удара» составляет примерно половину времени релаксации магнитной системы, как это показано в работе [15], посвященной ударному возбуждению при перемагничивании нормально намагниченной ферритовой пластины.

Как и при делении [1], такое ударное возбуждение упругой системы возможно только в сильно нелинейном режиме, когда амплитуда магнитных колебаний резко возрастает за незначительный промежуток времени, определяемый крайне высокой амплитудой возбуждающего сигнала. В линейном режиме нарастание магнитных колебаний происходит за время, определяемое временем магнитной релаксации, поэтому эффективность ударного возбуждения упругой системы значительно снижается и эффект умножения частоты отсутствует (раздел №8).

13. Линейная поляризация поля возбуждения. Общие положения

Случай линейной поляризации поля возбуждения отличается от случая круговой поляризации тем, что здесь прецессия вектора намагниченности происходит по эллипсу, так что нормальная к плоскости пластины составляющая намагниченности не остается постоянной, а меняется с двойной частотой, обеспечивая при достаточном уровне возбуждения богатый спектр гармоник. Поэтому умножение частоты здесь может происходить в установившемся стационарном режиме при любом времени, прошедшем после включения возбуждения.

Развитие колебаний во времени на достаточно большом его промежутке (до ) при линейной поляризации аналогично таковому при круговой поляризации, показанному на рис.2. Релаксация тех и других колебаний происходит с теми же временами, определяемыми параметрами затухания соответствующих систем. Различие состоит только в абсолютных значениях амплитуды магнитных и упругих колебаний в установившемся режиме далеко от начала возбуждения.  

Так в сильно нелинейном режиме при  и константе магнитоупругости  при времени порядка

в режиме круговой поляризации () при умножении частоты на два амплитуда магнитных колебаний составляет , а амплитуда упругих – , тогда как в режиме линейной поляризации (,  ) те же величины равны  ,  и   соответственно.

Можно видеть, что в обоих случаях амплитуда магнитных колебаний близка к максимальной длине нормированного вектора намагниченности (), так что намагниченность прецессирует вблизи плоскости пластины, что обусловлено весьма высоким уровнем возбуждения. Несколько меньшая величина амплитуды   по сравнению с  при  линейной поляризации отражает эллиптический характер прецессии за счет линейного возбуждения вдоль оси .

Значительный (более чем на порядок) рост амплитуды упругих колебаний при линейном возбуждении по сравнению со случаем кругового возбуждения обусловлен легкостью умножения частоты за счет генерации гармоник при эллиптическом характере прецессии.

Основные особенности умножения частоты возбуждения в промежутке времени между временами релаксации магнитных и упругих колебаний рассмотрены в работе [2]. Поэтому здесь, чтобы не дублировать результаты этой работы, будет рассмотрен интервал времени наблюдения, достаточно удаленный от начала колебаний, то есть такой, расположение которого значительно превышает времена релаксации как магнитных, так и упругих колебаний.

Аналогично первой части настоящей работы, посвященной делению частоты [1], положим интервал времени наблюдения следующим: , где, согласно данным работы [2], умножение частоты не наблюдалось (то есть явно не было выявлено, что, по-видимому, объясняется недостаточной чувствительностью примененных там методов).  

14. Роль нелинейности и величины константы магнитоупругого взаимодействия

Рассмотрим сначала, какую роль в процессе умножения частоты играет нелинейность и величина константы магнитоупругости. В качестве простейшего примера обратимся к случаю умножения частоты на два. Соответствующие развертки во времени магнитных и упругих колебаний иллюстрируются рис.7.

 

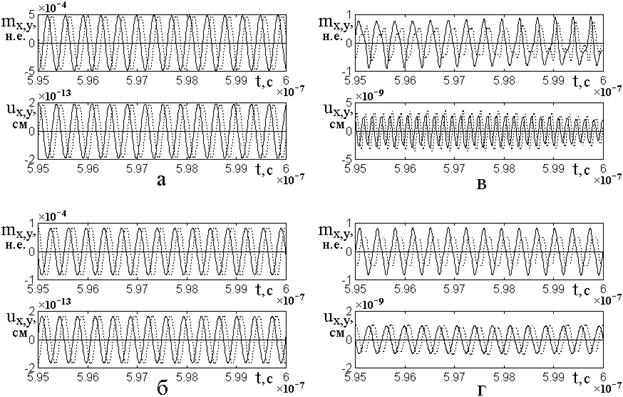
Рис.7. Развертки во времени магнитных и упругих колебаний  в пластине при различной величине константы  и уровне возбуждения.

Толщина пластины .

Сплошные линии – -компоненты, пунктирные линии – -компоненты.

а – ,  , ;

б – ,  , ;

в – ,  , ;

г – ,  , .

 

В левом столбце этого рисунка (а,б) показан чисто линейный режим возбуждения. Рис.7а соответствует сравнительно небольшой магнитоупругой связи, рис.7б – значительно (в пять раз) большей. Видно, что здесь во всех случаях как намагниченность, так и упругое смещение колеблются с частотой возбуждения, то есть какое-либо умножение частоты отсутствует.  

Увеличение магнитоупругой связи (рис.7б) приводит лишь к незначительному (менее ) уменьшению амплитуды магнитных колебаний, при этом амплитуда упругих колебаний также уменьшается на примерно такую же величину. Можно полагать, что такое одновременное уменьшение амплитуды тех и других колебаний свойственно чисто вынужденному полностью установившемуся режиму колебаний, имеющему место в достаточно удаленный от начала момент времени. В этом случае свободные колебания уже полностью затухли, так что перекачка энергии из магнитной систему в упругую и обратно отсутствует, а амплитуда тех и других колебаний полностью определяется величинами параметров того и другого затухания. 

Интересно отметить, что здесь, в отличие от случая деления частоты (работа [1], рис.6а,б), увеличения амплитуды упругих колебаний при увеличении константы  от  до , пропорционального увеличению константы (в пять раз), не происходит. Более того, дополнительное исследование показывает, что при удалении от исследуемого диапазона значений константы в обе стороны, то есть при  и  амплитуда упругих колебаний значительно падает, составляя в обоих случаях около . Таким образом, в исследуемом здесь случае умножения частоты, влияние константы магнитоупругости проявляется значительно более сложным, чем при делении, явно нелинейным образом.

Можно полагать, что в первом случае малой константы () амплитуда упругих колебаний мала просто потому, что связь является очень слабой вследствие малости самой константы. Относительно же второго случая большой константы () можно высказать предположение, что эффект умножения в любом случае обусловлен в первую очередь генерацией гармоник составляющей намагниченности, перпендикулярной плоскости пластины, происходящей за счет эллиптичности прецессии намагниченности. При этом в случае большой константы  намагниченность прецессирует почти в плоскости пластины, то есть указанная составляющая намагниченности мала и ее влияние в возбуждении упругих колебаний сказывается слабее, чем при константе средней величины.  

Замечание. Заметим, что высказанное здесь положение о решающей роли перпендикулярной намагниченности в процессе умножения является гипотетическим, то есть требует более серьезного исследования, в настоящий момент за рамки настоящей работы выходящего.

Рассмотрим теперь, как происходит процесс умножения в сильно нелинейном режиме, развертки колебаний во времени для которого показаны на рис.7в, соответствующем небольшой магнитоупругой связи () и на рис.7г при связи в пять раз большей ().

Можно видеть, что здесь в первом случае (рис.7в) магнитные колебания происходят с частотой возбуждения, однако компонента  (пунктир) имеет небольшую (около ) примесь второй гармоники. Упругие колебания при этом проявляют четко выраженный эффект удвоения частоты, причем составляющая основной частоты полностью отсутствует. 

Во втором случае (рис.7г) как магнитные, так и упругие колебания происходят с частотой возбуждения, причем, если магнитные (компонента ) еще и имеют незначительную (не более) примесь удвоенной частоты, то для упругих такая составляющая полностью отсутствует.

Этот факт является достаточно примечательным, однако он в какой-то степени согласуется с отмеченным выше для линейного режима наблюдением сильного уменьшения амплитуды упругих колебаний при значительном увеличении константы магнитоупругой связи. 

По-видимому, причина такого уменьшения амплитуды упругих колебаний при большой константе  – та же, что и в линейном режиме, то есть уменьшение роли компоненты намагниченности, перпендикулярной к плоскости пластины. 

Однако следует заметить, что в линейном случае такое уменьшение проявляется при аномально большом значении константы магнитоупругости (), в непосредственной близости от значения, соответствующего переориентации () [11], тогда как здесь колебания удвоенной частоты пропадают еще от переориентации на достаточном удалении.

Таким образом, из общего рассмотрения рис.7 можно заключить, что для реализации эффекта умножения частоты необходимы два условия: достаточно высокий уровень возбуждения () и умеренное значение константы магнитоупругого взаимодействия ().

15. Дополнительные свойства умножения частоты

Отметим еще некоторые свойства умножения частоты, из рис.7 непосредственно не следующие. Так дополнительное исследование показало, что при столь высоком уровне возбуждения как  удвоение частоты проявляется в достаточно чистом виде при весьма малых значениях константы магнитоупругого взаимодействия. Так при столь малом значении  как  амплитуда упругих колебаний на двойной частоте по компоненте  хотя и падает с  (при ) до , а по компоненте  с  до , однако примесь частоты возбуждения здесь полностью отсутствует.  Заметим, что в этих же условиях появляется более заметная (чем при ) примесь двойной частоты у колебаний намагниченности. Так по компоненте  она составляет , а по компоненте  достигает .

По уровню возбуждения удвоение частоты не является пороговым, однако переход колебаний упругого смещения от однократной частоты к двойной происходит в довольно узком интервале по амплитуде переменного поля. Так при  удвоение частоты еще полностью отсутствует, упругие колебания происходят только с частотой возбуждения. При  к основной частоте сильно примешивается двойная, составляя около , а при  в составе упругих колебаний основная частота уже полностью отсутствует, а остается лишь двойная в чистом виде. То есть при увеличении уровня возбуждения происходит постепенное вытеснение колебаний основной частоты с полным замещением колебаниями двойной частоты, причем такое замещение начинается и заканчивается в интервале  от  до .

Величина константы магнитоупругости в сторону уменьшения от  до  на границах этого интервала никак не сказывается. При увеличении  вплоть до  характер тех и других упругих колебаний практически  не меняется. При дальнейшем увеличении, начиная с , в составе упругих колебаний появляется составляющая основной частоты, которая постепенно вытесняет двойную, так что к  двойная частота основной полностью подавляется.

Во всем интервале от  до  амплитуда как магнитных, так и упругих колебаний не остается постоянной, а испытывает периодические биения с периодом около , причем глубина этих биений в середине интервала достигает , а к краям падает до нуля.

Таким образом, подавление упругих колебаний двойной частоты основной при увеличении константы магнитоупругости является также не пороговым, а достаточно плавным, однако происходит в довольно ограниченном диапазоне от до  через посредство постепенного замещения, сопровождаемого биениями амплитуды.  

16. Умножение с целочисленной кратностью

Рассмотрим теперь умножение частоты возбуждения в более общих случаях. Сначала обратимся к более простому умножению с целочисленной кратностью. Соответствующие развертки во времени колебаний намагниченности и упругого смещения, а также их параметрические портреты, показаны на рис.8. Аналогично случаю деления [1] взяты небольшие целочисленные значения кратности от  до . Учтены выявленные в предыдущем разделе условия реализации умножения: высокий уровень возбуждения () и умеренная величина константы магнитоупругого взаимодействия (). 

 

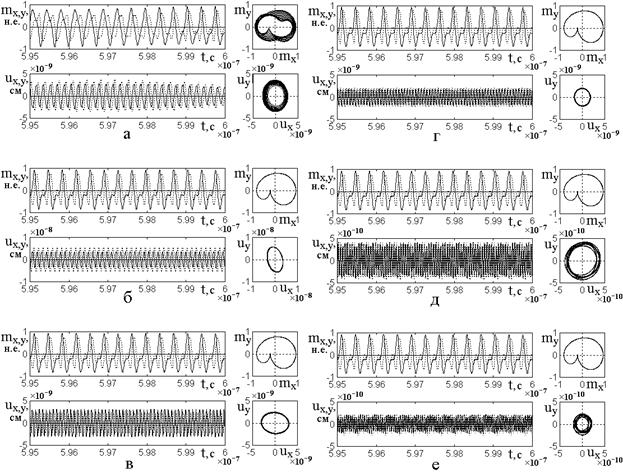
Рис.8. Развертки во времени магнитных и упругих колебаний, а также их параметрические портреты при различной целочисленной кратности умножения .

Толщина: , где .

Поляризация возбуждения линейная: , .

Сплошные линии – -компоненты, пунктирные линии – -компоненты.

Кратность: а –  ; б – ; в – ; г – ; д – ; е – .

Константа магнитоупругости: .

 

Из рассмотрения приведенных на рис.8 разверток для намагниченности и упругого смещения можно видеть, что здесь, в отличие от случая деления, серьезные различия видов колебаний при различных кратностях отсутствуют. Во всех случаях в колебаниях намагниченности преобладает составляющая основной частоты с незначительной (менее ) примесью второй гармоники. Более того, колебания намагниченности с кратностями от  до  практически идентичны. То же касается соответствующих им параметрических портретов.

Несколько отличаются только колебания, соответствующие кратности  (рис.8а), где в составе компоненты  (сплошная линия) примесь второй гармоники практически отсутствует, хотя в составе компоненты  (пунктир) вторая гармоника все же имеет место, но с амплитудой не более  от основной.

На общие колебания здесь в небольшой степени наложена низкочастотная составляющая с амплитудой примерно  от основной и периодом порядка . Так можно видеть, что а левой части верхней эпюры на рис.8а колебания компоненты  несколько (приблизительно на )   сдвинуты вниз, а в правой части – на столько же вверх от осевой линии. 

Можно полагать, что такая примесь низкочастотной составляющей обусловлена эффектом детектирования прецессии намагниченности, за счет своей эллиптичности в результате линейной поляризации возбуждения.

Благодаря присутствию такой низкочастотной составляющей параметрический портрет как для магнитных, так и упругих колебаний несколько размазывается. Так ширина кольца для магнитных колебаний составляет около  от радиуса, а для упругих – около . Наблюдаемые на портрете для намагниченности два внутренних завитка, по-видимому, обусловлены примесью второй гармоники, в первую очередь к компоненте .

Параметрические портреты для намагниченности при всех остальных кратностях не размазаны и имеют всего один внутренний завиток, что, по-видимому, происходит из-за того, что колебания второй гармоники примешиваются к основной частоте к обеим компонентам  и  в одинаковой степени.

Замечание. Наблюдаемый здесь на параметрических портретах для намагниченности внутренний завиток является чисто магнитным явлением с магнитоупругостью не связанным. Так дополнительная проверка показывает, что в отсутствие магнитоупругой связи при  он полностью сохраняется. Причина его состоит в сильной нелинейности магнитной системы при столь высоком уровне линейно поляризованного возбуждения как . Так при уровне возбуждения в  прецессия происходит по правильному эллипсу с полуосями  и  При уровне возбуждения  эллипс еще сохраняется, но несколько вытягивается вдоль оси , так что полуоси становятся равными  и , а при  на месте одной из коротких осей появляется плавный провал, который к  трансформируется в наблюдаемый здесь завиток с острой вершиной. При дальнейшем увеличении возбуждения с противоположной стороны эллипса появляется второй завиток, симметричный первому, так что к  оба завитка вершинами почти сходятся, образуя фигуру, похожую на восьмерку. Подробное исследование отмеченной здесь трансформации параметрического портрета при увеличении уровня возбуждения в известной авторам литературе отсутствует, однако поскольку такая трансформация представляет собой явление чисто магнитное, с упругостью не связанное, его рассмотрение за рамки настоящей работы выходит.  

Отметим однако, что завиток при , будучи чисто магнитным явлением, может вносить некоторое искажение в исследуемые здесь магнитоупругие процессы деления и умножения частоты. Тем не менее, как показано в разделе №14, выбор столь высокого уровня возбуждения для реализации эффекта умножения частоты является необходимым. Более того, в разделе №15 отмечается, что развитие умножения частоты на два происходит в том же диапазоне возбуждения, что и появление завитка (). Однако дополнительное исследование показало, что развитие умножения на три происходит в диапазоне более низком – около , где завиток отсутствует. Тем не менее, можно видеть, что вопрос о соотношении завитка с процессом умножения является более сложным и требует отдельного рассмотрения, за рамки настоящей работы выходящего. 

Возвращаясь к рассмотрению рис.8, отметим, что упругие колебания при всех рассмотренных здесь кратностях имеют ярко выраженную главную составляющую на частоте, соответствующей кратности умножения. Параметрические портреты при кратностях , ,  (рис.8б,в,г) практически не размазаны и имеют почти правильную эллиптическую форму, близкую к круговой.

Однако по мере увеличения кратности выше  эффективность процесса умножения падает. Так при кратности, равной  амплитуда упругих колебаний составляет , при  уже , а при  падает более чем на порядок – до . 

Колебания при кратностях  и  (рис.8д,е), оставаясь близкими к правильным на умноженной частоте, все же имеют небольшую примесь основной частоты, что приводит к некоторой размазке параметрических портретов. Так при кратности  (рис.8д) такая примесь составляет около , а при кратности  (рис.8е) возрастает до . Дополнительное исследование показывает, что при дальнейшем увеличении кратности составляющая основной частоты возрастает, постепенно вытесняя составляющую умноженной частоты. Такое вытеснение завершается при кратности , когда упругие колебания происходят уже только на частоте возбуждения и умножение частоты отсутствует. 

Итак, из проведенного рассмотрения можно видеть, что во всем исследованном диапазоне целочисленных кратностей (от  до ) колебания намагниченности происходят всегда на основной частоте с незначительной примесью второй гармоники, а колебания упругого смещения – всегда на умноженной частоте с незначительной примесью основной, заметной только при больших значениях кратности. При увеличении же кратности выше упомянутого диапазона основная частота в упругих колебаниях начинает преобладать, приводя при кратности порядка   к полному вытеснению умноженной. 

17. Умножение с дробной кратностью

Рассмотрим теперь умножение частоты возбуждения с дробной кратностью. Аналогично случаю деления [1] возьмем коэффициенты кратности равными ,   и . Соответствующие развертки во времени и параметрические портреты иллюстрируются рис.9. Левый столбец (а,б,в) здесь соответствует целочисленным кратностям , ,   и приведен для сравнения. В правом столбце (г,д,е) приведены кратности, увеличенные по сравнению с кратностями левого столбца на . 

 

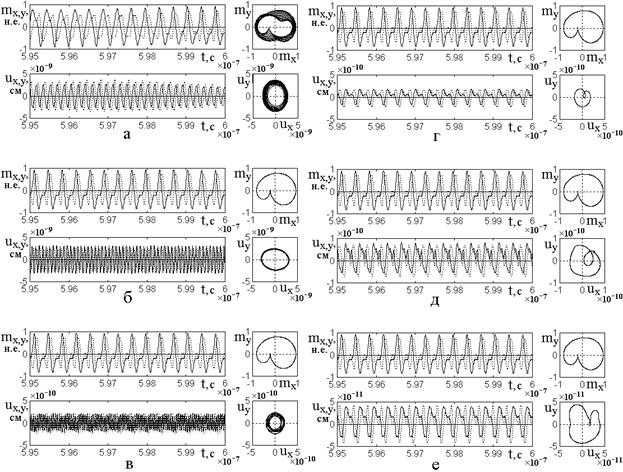
Рис.9. Развертки во времени магнитных и упругих колебаний, а также их параметрические портреты при различной дробной кратности умножения .

Толщина: , где .

Сплошные линии – -компоненты, пунктирные линии – -компоненты.

Кратность: а –  ; б – ; в – ; г – ; д – ;

е – .      Константа магнитоупругости: .

 

Можно видеть, что, как и при целых кратностях, развертки во времени и параметрические портреты для магнитных колебаний сохраняются неизменными, причем размазка параметрического портрета даже при  полностью отсутствует. 

Однако развертки и портреты для упругих колебаний существенным образом меняются. Так при целой кратности равной  (рис.9а) упругое смещение колеблется точно на удвоенной частоте. С другой стороны, при кратности всего на  большей, равной  (рис.9г), преобладает основная частота возбуждения с незначительной (около ) примесью двойной частоты. При этом колебания с частотой умноженной на  в явном виде не наблюдаются. Амплитуда упругих колебания также значительно (примерно в  раз) падает: с  при  (рис.9б) до  при  (рис.9г). Портрет не размазывается, однако на нем присутствует небольшой внутренний завиток, соответствующий примеси второй гармоники.

Аналогичным образом ведут себя упругие колебания и при других дробных кратностях. Так при  (рис.9д) амплитуда падает с  (рис.9б) до  (рис.9д), в развертке колебаний преобладает основная частота с незначительной (не более ) примесью более высокочастотных гармоник, а составляющая с умноженной частотой опять явно не выделяется. Портрет также содержит единственный внутренний завиток. 

При  (рис.9е) амплитуда падает с  (рис.9в) до  (рис.9е), в развертке колебаний преобладает основная частота с незначительной (не более ) примесью второй гармоники, а составляющая с умноженной частотой опять отсутствует. Наблюдаемый на портрете внутренний завиток опять остается единственным.

Таким образом, можно сделать вывод, что при задании толщины пластины, соответствующей дробной кратности, умножение частоты возбуждения с такой кратностью в явном виде не реализуется, а вместо него колебания упругого смещения происходят с основной частотой с незначительно примесью второй гармоники. При этом амплитуда таких колебаний по сравнению со случаем целочисленной кратности падает более чем на порядок.

Можно полагать, что наблюдаемое отсутствие умножения частоты с дробной кратностью обусловлено тем обстоятельством, что в спектре сильно нелинейных колебаний всегда в явном виде присутствуют только целочисленные гармоники [12-14]. В этом случае даже при задании толщины пластины, соответствующей дробной кратности, пластине как резонатору не остается возможности выделять что-либо из общего спектра частот, так как дробные частоты там просто отсутствуют.    

Замечание. Следует заметить, что в работе [2], посвященной исследованию умножения в интервале между временами релаксации магнитных и упругих колебаний, также отмечалось определенное ухудшение умножения с дробной кратностью по сравнению с целочисленной. Хотя там возбуждение умноженной частоты происходило, по-видимому, главным образом за счет ударного механизма, все же можно полагать, что даже ударное возбуждение обогащает спектр дробных частот недостаточным образом. Более подробное исследование этого вопроса, хотя и представляет определенный интерес, но за рамки настоящей работы выходит.

Заключение

Применительно к геометрии магнитострикционного преобразователя рассмотрены связанные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами, возбуждаемые переменным магнитным полем, частота которого совпадает с частотой ферромагнитного резонанса магнитной подсистемы. Показано, что в случае, когда резонансная частота упругой подсистемы превышает в кратное число раз резонансную частоту магнитной подсистемы, возможно возбуждение упругих колебаний на частоте, соответствующей частоте упругого резонанса, что представляет собой процесс умножения исходной частоты в кратном отношении.

Рассмотрены два варианта реализации умножения частоты: первый – при возбуждении переменным полем круговой и второй – линейной поляризации. Показано, что в случае круговой поляризации решающую роль играют процессы релаксации магнитных и упругих колебаний, поэтому важно соотношение между моментом включения возбуждения и временем наблюдения явления, причем время релаксации упругой системы должно  значительно превышать время релаксации магнитной. 

В случае линейной поляризации подобная зависимость отсутствует, так что устойчивое умножение частоты наблюдается в любой момент времени, в том числе значительно удаленный от момента включения возбуждения. В качестве причины такого различия выдвинуто предположение о решающей роли характера прецессии намагниченности, при круговой поляризации представляющей собой правильный круг без гармонических составляющих, а при линейной – эллипс, сопровождаемый генерацией множества гармоник.   

Отмечено, что причиной умножения частоты при круговой поляризации являются биения между частотами собственных колебаний упругой системы и переменного поля, имеющие место только в начальный момент времени после включения возбуждения, причем механизмом, обеспечивающим биения, является ударное возбуждение упругой системы за счет кратковременного воздействия магнитной.

На примере умножения частоты на два при круговой поляризации рассмотрено формирование магнитных и упругих колебаний во всем интервале времен от начала возбуждения до окончания релаксации упругой системы. Показано, что при линейном возбуждении происходит периодическая перекачка энергии из магнитной системы в упругую и обратно. Выявлен эффект формирования затухания упругой системы за счет магнитной, приводящий к выравниванию времени релаксации обеих систем вместе. При нелинейном возбуждении преобладает ударное возбуждение упругой системы за счет магнитной, как раз ответственное за эффект умножения частоты. 

На примере рассмотрения малого промежутка времени, заключенного между временами релаксации магнитной и упругой систем, показано, что необходимыми условиями реализации эффекта умножения частоты являются: соответствие толщины пластины резонансу на частоте, получаемой в результате умножения, а также достаточно высокий уровень возбуждения обеспечивающий сильное проявление нелинейности системы.

Рассмотрено умножение частоты с целочисленной кратностью. Показано, что оптимальным относительно максимума амплитуды умноженной частоты является интервал времени посередине между временами релаксации магнитной и упругой систем, причем упругие колебания умноженной частоты проявляются на фоне колебаний основной частоты, составляя по амплитуде до . Выявлено, что в интервале кратностей от  до  примесь умноженной частоты к основной испытывает периодические колебания, проявляясь сильнее при четных кратностях. При кратностях от  до  колебания умноженной частоты постепенно спадают, уступая свое место колебаниям основной.

Рассмотрено умножение частоты с дробной кратностью, выявлен его сложный характер, проявляющийся в значительном изменении примеси умноженной частоты к основной уже при малом изменении кратности. Показано, что наиболее эффективное умножение частоты имеет место при кратности равной , где амплитуда умноженной частоты составляет около  от амплитуды основной. Полученные результаты обсуждены с точки зрения гипотезы ударного возбуждения упругой системы за счет магнитной. Отмечено хорошее согласование положений гипотезы с наблюдаемыми свойствами умножения частоты, однако отмечены некоторые моменты, требующие дополнительного исследования.  

Рассмотрено умножение частоты при линейной поляризации переменного поля, имеющее место при любом удалении времени наблюдения от начала возбуждения, в первую очередь превышающем времена релаксации магнитной и упругой систем. Выявлено, что в этом случае эффективность умножения частоты при целочисленной кратности значительно выше, чем при круговой поляризации, что обусловлено легкостью генерации гармоник за счет эллиптической прецессии намагниченности. 

На примере умножения частоты на два показано, что для успешной реализации эффекта умножения необходимы два условия: достаточно высокий уровень возбуждения и умеренное значение константы магнитоупругого взаимодействия. Отмечено, что как при малой, так и при чрезмерно большой константе эффективность умножения значительно падает, в первом случае – из-за малости связи магнитной и упругой систем, а во втором – из-за приближения прецессии намагниченности к плоскости пластины, в результате чего эффект генерации гармоник снижается.

Рассмотрено умножение частоты с целочисленной кратностью. Установлено, что в пределах кратности от  до , в отличие от случая круговой поляризации, при линейной поляризации упругие колебания умноженной частоты проявляются в чистом виде без заметной примеси основной частоты. При кратностях от  до  наблюдается присутствие основной частоты, проявляющееся тем сильнее, чем кратность выше, а при дальнейшем увеличении кратности составляющая умноженной частоты пропадает, полностью заменяясь основной.

Рассмотрено умножение частоты с дробной кратностью. Выявлено, что при дробной кратности, в отличие от случая круговой поляризации, при линейной поляризации эффект умножения частоты практически отсутствует. В качестве предположения о причине такого отсутствия при дробной кратности отмечено, что при линейной поляризации эффект умножения обусловлен в первую очередь генерацией гармоник в нелинейном режиме, кратность которых по своей природе может быть только целочисленной.

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

 

Литература

1. Власов В.С., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2015. №9. С.1-45. http://jre.cplire.ru/jre/sep15/4/text.html, http://jre.cplire.ru/jre/sep15/4/text.pdf.

2. Власов В.С., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.153.

3. Власов В.С., Шавров В.Г., Щеглов В.И. // Материалы школы-конференции «XVI Международная зимняя школа-семинар по радиофизике и электронике сверхвысоких частот». Саратов: ООО «Издательский центр «Наука». 2015. С.33. 

4. VlasovV.S., Kotov L.N., Shavrov V.G., Shcheglov V.I. // Book of Abstracts “20th International conference on magnetism”. Barcelona. 5-10 july 2015. P.872.  

5. Власов В.С., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.139.

6. Власов В.С., Шавров В.Г., Щеглов В.И. // Материалы школы-конференции «XVI Международная зимняя школа-семинар по радиофизике и электронике сверхвысоких частот». Саратов: ООО «Издательский центр «Наука». 2015. С.32. 

7. Власов В.С. Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Дисс. на соискание уч. степ. к.ф.-м.н. Москва. МГУ. 2007.

8. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сб. тр. XVI Международной конференции "Радиолокация и радиосвязь". Москва-Фирсановка. Изд. МЭИ. 2008. С.197.

9. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.

10. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.

11. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.

12. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М., Наука, 1978.

13. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Советское радио. 1964.

14. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Радио и связь. 1986.

15. Власов В.С., Шавров В.Г., Щеглов В.И. // РЭ. 2014. Т.59. №6. С.572.

16. Власов В.С., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2013. С.177.

17. Власов В.С., Шавров В.Г., Щеглов В.И. // Сборник материалов X Международной зимней школы-семинара «Хаотические автоколебания и образование структур» (ХАОС-2013). Саратов (7-12 октября 2013 г.). Изд. центр «Наука». 2013. С.66.

18. Власов В.С., Шавров В.Г., Щеглов В.И., Плешев Д.А. // Тезисы докладов международной зимней школы физиков-теоретиков – «Коуровка-XXXV» (23.02-01.03.2014). Екатеринбург:  ИФМ УрО РАН. 2014. С.89.

19. Suhl H. // IEEE Trans on Magn. 1998. V.34. №4. P.1834-1838.

20. Vittoria C., Yoon S.D., Widom A. // Phys. Rev. B. 2010. V.81. №1. P.014412(6).

21. Ветошко П.М., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.237.

22. Ветошко П.М., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2014. №11. С.1-56. http://jre.cplire.ru/jre/nov14/1/text.html, http://jre.cplire.ru/jre/nov14/1/text.pdf.

23. Ветошко П.М., Шавров В.Г., Щеглов В.И. // ПЖТФ. 2015. Т.41. №21. С.1.

24. Ветошко П.М., Шавров В.Г., Щеглов В.И. // Электронный «Журнал радиоэлектроники». 2015. №8. С.1-33. http://jre.cplire.ru/jre/aug15/5/text.html, http://jre.cplire.ru/jre/aug15/5/text.pdf.

25. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос.Изд.физ.-мат.лит. 1960. 

26. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973..

27. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.