Восстановление спектрально-ограниченного сигнала по его известной части
В. А. Коротков
ИРЭ им. В.А. Котельникова РАН, г. Фрязино Московской области
Получена 9 сентября 2013 г.
Аннотация. В работе рассмотрена возможность восстановления спектрально-ограниченного сигнала по известной его части.
Ключевые слова: восстановление сигналов, спектры, спектрально-ограниченные сигналы.
Abstract. The possibility of restoration of spectral-limited signal from its well-known part is considered in the work.
Key words: restoration of signals, spectra, spectral-limited signals.
В данной работе рассматривается попытка восстановления спектрально-ограниченного сигнала по известной части одномерного сигнала. Посылом для выполнения данной работы явилось то соображение, что ограниченная часть спектра сигнала содержит всю информацию для воссоздания сигнала вообще говоря неограниченной длины. Следовательно, в этом сигнале исходный спектр ограниченной длины известным образом копируется с соответствующими коэффициентами неограниченное количество раз. Понятно, что если по ограниченному отрезку сигнала мы сможем восстановить весь этот ограниченный спектр, то затем можно будет восстановить сигнал по всей длине.
Если на сигнал не накладывать условия спектральной ограниченности, то вышеуказанные соображения не работают. В [4] показано, что доопределяя в области, где сигнал неизвестен, другим сигналом, получим результирующий сигнал, совпадающий с исходным только в известной части. Таким образом, требование спектральной ограниченности для возможности восстановления всего сигнала по известной его части является обязательным.
Проверим это. Пусть исходный сигнал представляет собой белый шум. Этот сигнал и его спектр представлены соответственно на Рис.1-2.
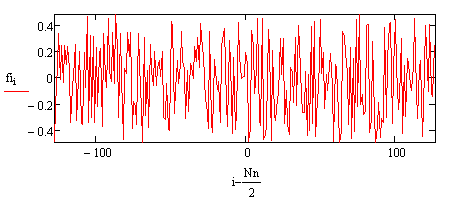
Рис.1. Исходный сигнал. Nn=256 – общее количество пикселей.
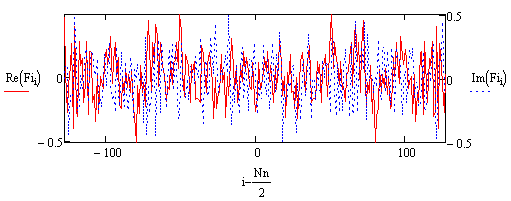
Рис.2. Спектр исходного сигнала.
Ограничим теперь этот спектр. Полученные спектр и спектрально-ограниченный сигнал представлены соответственно на Рис.3-4.

Рис.3. Спектр спектрально-ограниченного сигнала. No=65 – ширина спектра.
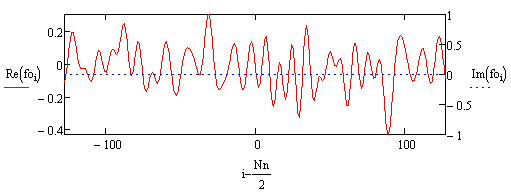
Рис.4. Спектрально-ограниченный сигнал.
Если теперь мы представим процедуру получения сигнала на Рис.4 из спектра на Рис.3 в виде перемножения матрицы A, соответствующей обратному преобразованию Фурье, на вектор F, содержащий данные спектра на Рис.3, то сигнал f или любую его часть можно вычислить по формуле:
f = A * F. (1)
Понятно, что если нам известен сигнал f, то можно, решив систему уравнений (1), вычислить спектр F. Теперь встает закономерный вопрос о том, какой длины надо взять сигнал f, для того, чтобы достаточно точно определить спектр F? Минимальная длина понятна – меньше чем количество пикселов в спектре брать бессмысленно. Необходимая длина завязана на точность измерений, точность вычислений и то, какая доля энергии входит в измеряемую область по отношению к полной энергии спектрально-ограниченного сигнала. Оставим вопрос о необходимой длине на будущее. А сейчас в качестве измеренной области возьмем область длиной в 128 пикселей – ровно половину от целого сигнала.
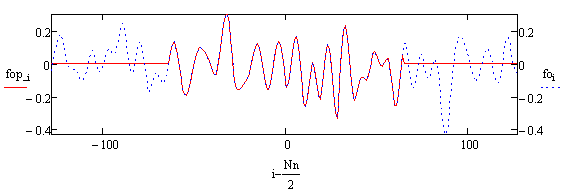
Рис.5. Измеренный сигнал – красная линия и полный спектрально-ограниченный сигнал – синяя линия.
Ну а теперь сформируем матрицу A в формуле (1). Если в качестве f из (1) взять fop из Рис.5, то из решения (1) по методу наименьших квадратов с помощью метода SVD получим спектр F (Рис.6-7).
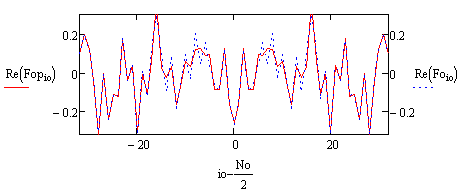
Рис.6. Реальная часть спектра, полученного решением (1) – красная линия, реальная часть исходного спектра – синяя линия.

Рис.7. Мнимая часть спектра, полученного решением (1) – красная линия, мнимая часть исходного спектра – синяя линия.
Знание спектра позволяет с помощью преобразования Фурье восстановить полный сигнал. Результат этой операции представлен на Рис.8.
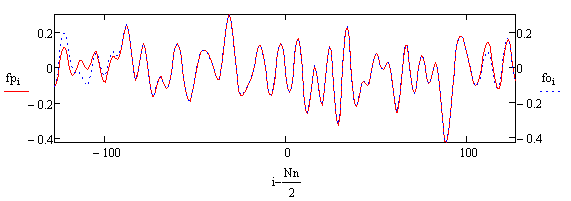
Рис.8. Восстановленный сигнал – красная линия, исходный спектрально ограниченный сигнал – синяя линия.
Понятно, что чем дальше находится восстанавливаемые значения сигнала от известных измеренных значений, тем ошибка в восстановлении больше. В данной работе рассматривался спектрально-ограниченный сигнал, у которого спектр получен из белого шума.
Теперь рассмотрим немного другой входной сигнал и проделаем над ним все те же манипуляции. Итак, исходный сигнал Рис. 9-10.
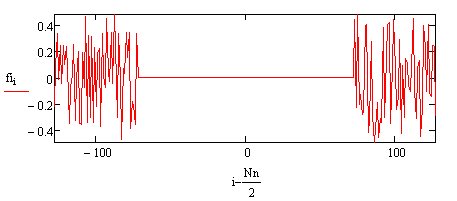
Рис.9. Исходный сигнал. Nn=256 – общее количество пикселей.
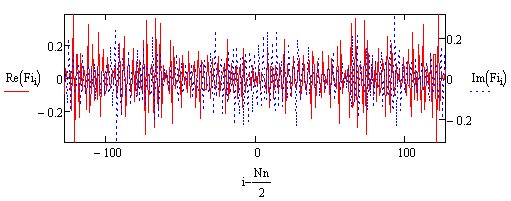
Рис.10. Спектр исходного сигнала.
Практически, это такой же шумовой сигнал, как и на Рис.1-2, только вырезана та область сигнала, которая в дальнейшем будет использоваться как область измеренного сигнала.
Ограничим теперь этот спектр. Полученные спектр и спектрально-ограниченный сигнал представлены соответственно на Рис.11-12.
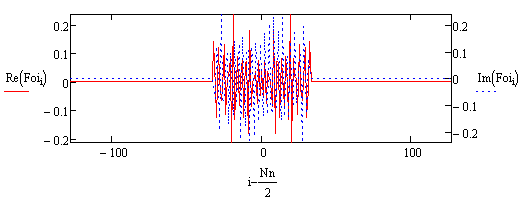
Рис.11. Спектр спектрально-ограниченного сигнала. No=65 – ширина спектра.

Рис.12. Спектрально-ограниченный сигнал
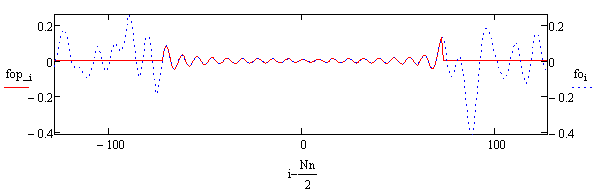
Рис.13. Измеренный сигнал – красная линия и полный спектрально-ограниченный сигнал – синяя линия. Измеряется только та область сигнала, где до фильтра сигнал был равен нулю.

Рис.14. Реальная часть спектра, полученного решением (1) – красная линия, реальная часть исходного спектра – синяя линия
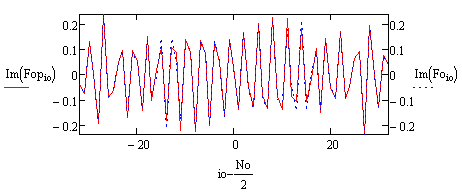
Рис.15. Мнимая часть спектра, полученного решением (1) – красная линия, мнимая часть исходного спектра – синяя линия
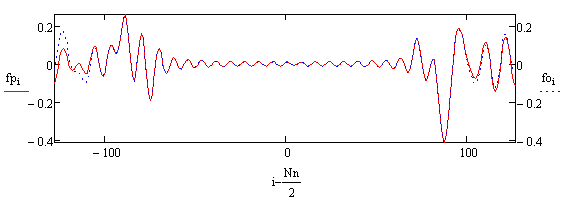
Рис.16. Восстановленный сигнал – красная линия, исходный спектрально ограниченный сигнал – синяя линия.
Таким образом очевидно, что если до фильтра отдельные области исходного сигнала могут иметь существенно разные свойства, то после фильтра сигнал меняется. Каждая его часть содержит информацию обо всем сигнале. Другое дело то, что использовать эту информацию можно только проделав определенные манипуляции и имея информацию о свойствах фильтра (полосе пропускания). При этом необходимо учитывать, что конечно же общие свойства сигнала у отдельных его частей создаются фильтром. Однако, если эти общие для отдельных частей сигнала свойства были и до фильтра, то восстановление проходит легче (область измеренного сигнала может быть выбрана меньше). Например, в случае сигналов на рис.4 и рис.12 области для измеренного сигнала выбирались соответственно 128 и 144.
Автор искренне благодарен Зражевскому А.Ю. за постановку задачи, полезные и своевременные рекомендации и за обсуждение и горячую поддержку во время исследования и написания работы.
1. В.А.Зверев. Радиооптика. М. «Советское радио». 1975г.
2. Зражевский А. Ю., Коротков В. А. Восстановление одномерных финитных сигналов, прошедших через фильтр низких частот. // Журнал радиоэлектроники: электронный журнал. 2013. N3. URL: http://jre.cplire.ru/jre/mar13/10/text.pdf
3. Зражевский А. Ю., Коротков В. А. Исследование восстановления сигнала, прошедшего через неидеальный фильтр низких частот. // Журнал радиоэлектроники: электронный журнал. 2013. N4. URL: http://jre.cplire.ru/jre/apr13/8/text.pdf
4. Аксенов. Математический анализ. (Ряды Фурье. Интеграл Фурье. Суммирование расходящихся рядов.) Учебное пособие. СПб.: Изд-во «Нестор», 1999 г.