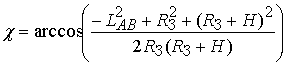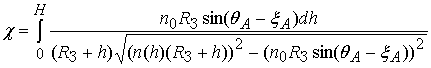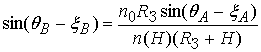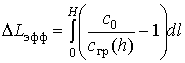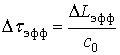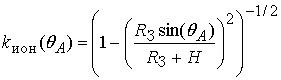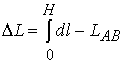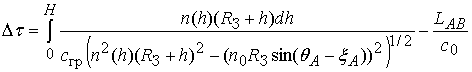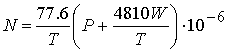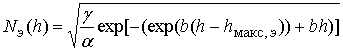УДК 621.391.01

ХАРАКТЕРИСТИКИ ИОНОСФЕРНЫХ И ТРОПОСФЕРНЫХ ЛИНИЙ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ

 

Л. Е. Назаров, В. В. Батанов, З. Т. Назарова

Институт радиотехники и электроники им. В.А.Котельникова РАН, Фрязинский филиал

Статья получена 8 сентября 2015 г.

 

Аннотация. В статье рассмотрен ряд моделей линий передачи, включающих влияние ионосферы и тропосферы на распространение сигналов. Тропосфера и ионосфера определяют временную задержку прохождения сигналов вследствие отличия скорости распространения радиоволн от скорости света в свободном пространстве и явления рефракции, дополнительное доплеровское смещение частоты.

Ключевые слова: ионосфера, тропосфера, рефракция, временная задержка.

Abstract. This paper presents description for models of tropospheric and ionospheric satellite communication channels. These models deals with radio wave signal propagation effects in atmosphere including refraction, Doppler frequency shift and time delay.

Key words: ionosphere, troposphere, refraction, time delay.

 

Введение

Характеристики и свойства линий передачи, модели которых используются при проектировании систем связи, являются базовыми для разработки оптимальных (либо близких к оптимальным) сигнальных конструкций с использованием схем помехоустойчивого кодирования и алгоритмов их обработки в приемных устройствах [1-5].  При распространении по рассматриваемым в настоящей статье линиям спутниковых систем связи (системы фиксированной, мобильной, персональной связи) сигналы подвергаются действию искажающих факторов, основными из которых являются следующие [6-8]:

- влияние атмосферы (ионосфера, тропосфера);

- многолучевость за счет рассеяния, дифракции и отражения сигналов;

- доплеровское смещение и уширение спектра сигналов;

- нестационарность линий передачи;

- нелинейность передающего устройства;

- наличие аддитивного шума.

Созданию и развитию класса моделей относительно действия приведенных факторов посвящен ряд работ [1,2,8]. Использование этих моделей дает возможность определить значения энергетических потерь при распространении сигналов и оценить эффективность проектируемых спутниковых систем связи (оценивание вероятностных характеристик, целостности связи) [2,9,10].

В статье рассмотрен ряд моделей линий передачи, включающих влияние ионосферы и тропосферы на распространение сигналов. Тропосфера и ионосфера определяют задержку прохождения сигналов вследствие отличия скорости распространения радиоволн от скорости света в свободном пространстве и явления рефракции [8]. Кроме того, из-за рефракции происходит изменение доплеровского смещения несущей частоты и тактовой частоты сигналов с цифровой манипуляцией. Случайные изменения физических свойств тропосферы и ионосферы обусловливают вариации фаз (частот) и амплитуд радиосигналов, что определяет важный параметр линий передачи - их временную стационарность. С использованием рассмотренных моделей произведены численные оценки этих характеристик линий передачи для различных частотных диапазонов.

1. Постановка задачи

В соответствии с Регламентом радиосвязи для каналов спутниковых систем связи выделены P-, L-, S-, Ka- частотные диапазоны (длины волн 1…100 см), интенсивно осваиваются другие частотные диапазоны [11]. При распространении радиоволн этих диапазонов, использовании ориентированных высоконаправленных антенн пренебрегают влиянием поверхности Земли и учитывают влияние тропосферы и ионосферы на распространение радиоволн, которое выражается в следующих явлениях:

- лучевые линии отклоняются на угол рефракции;

- увеличивается время распространения сигналов между передатчиком и приемником по отношению к времени распространения в вакууме;

- происходят временные изменения амплитуды, фазы, частоты колебаний, определяющие стационарность линий передачи;

- происходит поворот плоскости поляризации радиоволн.

 

 

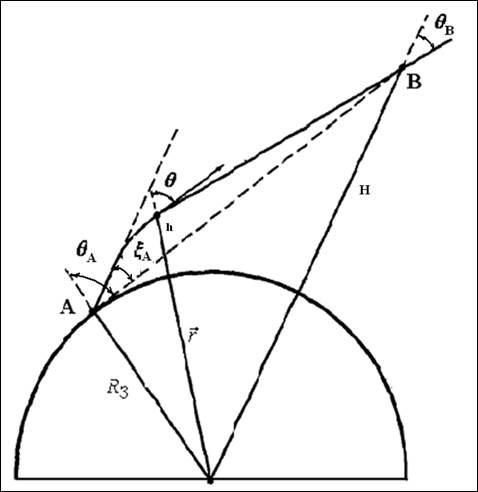
Рис.1. Схема распространения радиоволн при передаче сигналов земной станцией (точка А) и приеме сигналов спутником (точка В).

 

Отмеченные факты влияния тропосферы и ионосферы определяются пространственным распределением и временными вариациями коэффициента преломления сред  ( - приведенный коэффициент преломления). Для анализа распространения сигналов рассматриваемых частотных диапазонов применяется теория лучевого представления, которая дает достаточно точные решения волнового уравнения [8]. В этом случае для модели плавно-неоднородной сферически симметричной среды закон преломления представляется соотношением [7,8]

.                                       (1)

Здесь  - радиус Земли,  - высота над земной поверхностью,  - угол между направлением лучевой линии и радиусом вектором . На рис.1 приведена схема распространения радиоволн при передаче сигналов земной станцией (точка А) и приеме сигналов спутником (точка В).

На основе соотношения (1) оцениваются параметры моделей линии передачи «земная станция - спутник»:

-углы рефракции , определяющие энергетические потери при передаче и приеме сигналов за счет отклонения диаграммы направленности антенн земной станции и спутника;

- дополнительное доплеровское смещение несущей частоты и тактовой частоты сигналов с цифровой манипуляцией;

-различие расстояния от передатчика до приемника  вдоль луча распространения от истинного расстояния прямой видимости, обусловленное рефракцией лучевой линии;

- различие времени распространения вдоль луча и времени распространения вдоль линии прямой видимости со скоростью света в вакууме , определяемое тем, что существует различие этих путей распространения и отличие групповой скорости распространения в среде от .

Учет этих факторов требуется при разработке спутниковых систем связи с временным, кодовым, частотным разделением сигналов, а также при оценке энергетических потерь за счет искажающего влияния рассматриваемых сред распространения [1].

Цель работы - рассмотреть методы оценивания приведенных факторов влияния ионосферы и тропосферы при распространении сигналов по спутниковым линиям передачи сигналов с использованием модельных описаний сред, привести примеры расчетов с использованием данных методов.

2. Методы вычисления параметров спутниковых линий за счет влияния ионосферы и тропосферы

Ниже приведены методы расчета рассмотренных выше параметров моделей линии передачи «земная станция - спутник».

Для оценивания угла рефракции  в точке А известен ряд аналитических выражений. В работе [7] даны выражения для оценивания

,                                    (2)

.         (3)

Здесь  - коэффициент преломления на высоте ;  - истинный зенитный угол направления на антенну спутника;  - высота спутника.

Более сложное выражение для оценки , использующее градиент коэффициента преломления , приведено в [8]

.  (4)

Значение угла рефракции  для спутника в точке В определяется на основе соотношения (1)

.                                   (5)

 

Здесь  - истинный зенитный угол линии ОВ.

Следует отметить, что с достаточной степенью точности результирующий угол рефракции  вычисляется как сумма углов рефракции за счет влияния тропосферы и ионосферы [7].

Угол рефракции  определяет энергетические потери  при передаче сигналов за счет отклонения диаграммы направленности антенны земной станции  от линии АВ. Подобная оценка энергетических потерь  вычисляется при приеме сигналов за счет отклонения диаграммы направленности антенны спутника  от линии ВА.

Угол рефракции  определяет дополнительное доплеровское смещение  несущей частоты  (тактовой частоты сигналов с цифровой манипуляцией) относительно доплеровского смещения в вакууме

.                                  (6)

 

Здесь  - длина волны в вакууме;  - длина волны в точке В;  - скорость спутника;  - единичный вектор, касательный к АВ;  - единичный вектор, касательный к лучу распространения в точке В;  - скалярное произведение  и .

При решении кинематических задач радиотехническими методами (например, при определении расстояния до спутника либо при решении задач навигации), а также при вычислении характеристик ионосферных и тропосферных линий спутниковых систем связи (например, вычисление временных задержек) возникают ошибки оценивания метрических расстояний либо времени задержки. Эти ошибки обусловлены отличием групповой скорости распространения радиоволн  от скорости распространения в вакууме , а также искривлением луча относительно прямолинейного распространения в соответствии с (1). В приложениях влияние эффекта искривления полагается малым, в этом случае рассматривается различие эффективного пути распространения  вдоль луча АВ и вдоль прямой АВ определяется соотношением [7,8,9]

.                                                    (7)

Здесь .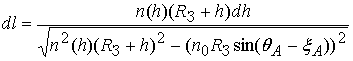

 

Соответствующее различие времени распространения  имеет вид

.                                                                  (8)

Приближенное оценивание значений  можно осуществить на основе значений , вычисленных с использованием соотношения (8) в сочетании с корректирующими коэффициентами  [8]

.                          (9)

Корректирующие коэффициенты для тропосферы  и ионосферы  задаются соотношениями [8,12]

,                                                (10)

.                        (11)

Выражение для  с учетом искривления луча из-за рефракции радиоволн имеет вид

.                                                       (12)

Здесь  - расстояние АВ, вычисляемое с использованием тригонометрических соотношений для треугольника ОАВ и угла .

Результирующее выражение для  имеет вид

.   (13)

Различие времени распространения задается соотношением

.   (14)

Здесь  - угол рефракции, вычисляемый с использованием (2)-(5).

3. Модели тропосферы

Значение  для модельного описания коэффициента преломления тропосферы  определяется ее параметрами: давлением  (миллибары), температурой  и влажностью  [6,7]

.                                      (15)

 

Следует отметить отсутствие в (15) зависимости от частоты.

Модельное описание высотного профиля  задается выражением

.                                                    (16)

Здесь  - высота над земной поверхностью. Вблизи земной поверхности параметр  зависит от климатических и метеорологических условий  и принимает значения в пределах . В нормальной тропосфере для средних широт градиент изменения  составляет , то есть значения параметра   [7]. В практических приложениях значения параметров  и  оцениваются по приземным значениям , , .

Ряд более сложных моделей тропосферы приведен в работах [13,14].

4. Модели ионосферы

Ионосферой называют ионизированную область атмосферы на высоте более 60 км над земной поверхностью [6,7]. В качестве верхней границы ионосферы принимают область высот 15…20 тыс.км.

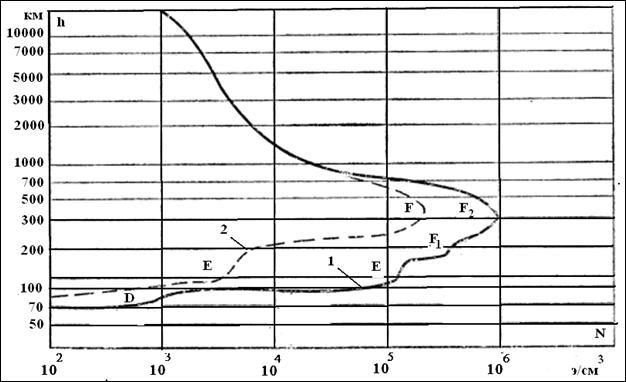
В результате экспериментальных исследований получены достаточно полные сведения о строении ионосферы и ее характеристиках [6,7,8]. На высоте 250…400 км имеется основной максимум ионизации, выше и ниже которого электронная плотность  убывает. Область ниже основного максимума называется внутренней, а выше - внешней ионосферой. Пример типичного профиля электронной плотности ионосферы дан на рис.2 [7].

 

Рис.2. Профиль электронной плотности ионосферы (1 - днем, 2 – ночью).

 

Во внутренней ионосфере обычно существует ряд локальных максимумов электронной плотности, называемых слоями - D, E, F [6,7]. Эти слои характеризуются параметрами - максимумом электронной плотности ; высотой нижней границы слоя ; полутолщиной слоя; коэффициентом рекомбинаций  (). Ниже дается общая характеристика этих параметров для слоев.

Слой D расположен на высоте 60…80 км, ночью слой исчезает. Электронная плотность не превышает  , число столкновений достигает , коэффициент рекомбинации .

Слой E расположен на высоте 95…100 км, полутолщина составляет 15…20 км, электронная плотность  днем и  ночью; число столкновений ; коэффициент рекомбинации  днем и  ночью.

Слой F расположен на высоте 250…400 км. В зимнее время электронная плотность достигает  днем и  ночью. Полутолщина слоя достигает 100…200 км.

Летом в дневное время слой F расщепляется на два слоя . Слой  расположен на высоте 300…400 км, слой  на высоте 200…230 км . Электронная плотность слоя  достигает , для слоя  . В ночное время существует лишь один слой на высоте 300 км с параметрами , , , полутолщина 100…200 км.

Выше основного максимума электронной плотности (слой F) электронная плотность падает, изменяясь в диапазоне высот 500…1000 км от  до  . В диапазоне высот 1700…10000 км электронная плотность остается в пределах  , на высоте более 15000 км электронная плотность монотонно спадает и на высоте 20000 км достигает  .

Разработке и развитию моделей профиля электронной плотности посвящены работы [6,7,15,16]]. Наиболее разработанными являются глобальные трехмерные физические модели, их принципы построения и входные параметры даны в работах [16,17,18].

Наиболее простая модель профиль электронной плотности ионосферы , используемая ниже для оценки характеристик линий передачи спутниковых систем связи, задается аналитическим соотношением [6]

.                (17)

Здесь  - параметры модели;  - коэффициент рекомбинации;  - высота над земной поверхностью, для которой достигается максимальное значение электронной плотности ионосферы.

При выполнении условия  известно соотношение относительно диэлектрической проницаемости ионосферы  [7]

.                                                        (18)

В этом случае проводимостью ионосферы в исследованиях пренебрегают, то есть ионосфера полагается идеальным диэлектриком и для высоких частот справедливо соотношение  [6,7].

5. Результаты оценивания характеристик линий передачи спутниковых систем связи

Для оценивания характеристик линий передачи спутниковых систем связи использовалась модель тропосферы с приведенным коэффициентом преломления  в виде (16), параметры модели  соответствовали приведенным в п.3 параметрам нормальной тропосферы для средних широт. Для ионосферы использовалась модель профиля электронной плотности  в виде (17), параметры модели  соответствовали аппроксимации профиля  на рис.2 для дневного времени,  км. Вычисление интегральных соотношений произведено с использованием численного метода Симпсона с повышенной точностью [19].

В таблице 1 приведены оценки углов рефракции , , вычисленные с использованием соотношений (3) и (4) соответственно, в зависимости от зенитного угла . Высота спутника  км, центральная частота  МГц и  ГГц. При увеличении зенитного угла  значения углов рефракции  увеличиваются и при  достигают значений . Видно также, что основной вклад в рефракцию вносит тропосфера - влияние ионосферы существенно менее эффективно (примерно в 5-8 раз для  МГц и в 70-120 раз для  ГГц). Для значений центральной частоты  ГГц влияние ионосферы на рефракцию можно считать относительно малым.

Таблица 1. Значения оценок углов рефракции ,  в зависимости от зенитного угла
(вычисление ,  произведено с использованием (3) и (4) соответственно).

, град	км,  МГц				км, ГГц
	Тропосфера		Ионосфера		Ионосфера
	,град	,град	,град	,град	,град	,град
0	0	0	0	0	0	0
10	0.00460	0.00458	0.00166	0.0013	0.00012	0.00010
20	0.0096	0.0093	0.00343	0.0028	0.00024	0.00020
30	0.0151	0.0146	0.00541	0.0045	0.00039	0.00029
40	0.0220	0.0214	0.00781	0.0062	0.00056	0.00044
50	0.0312	0.0304	0.01093	0.0087	0.00078	0.00061
60	0.0450	0.0436	0.01541	0.0120	0.00109	0.00086
70	0.0710	0.0688	0.02261	0.0170	0.00161	0.00121
80	0.1410	0.1350	0.03513	0.0240	0.00249	0.00171
85	0.25303	0.2372	0.04318	0.0265	0.00306	0.00189

 

На рис.3 приведены зависимости угла рефракции  за счет влияния ионосферы от высоты  спутника для центральной частоты  МГц. Кривая 1 соответствует зенитному углу , кривая 2 зенитному углу . Видно, что при  км наблюдается максимум рассматриваемой зависимости. Видно также, что при  км угол рефракции практически не зависит от параметра .

 

Рис.3. Зависимости угла рефракции  за счет влияния ионосферы от высоты  спутника
(центральная частота  МГц):
кривая 1 – зенитный угол ; кривая 2 – зенитный угол .

В таблице 2 приведены оценки энергетических потерь  для максимального угла рефракции  в зависимости от размера  прямоугольной апертуры антенны (центральная частота  МГц, длина волны  м). Здесь 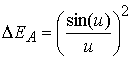,  [13]. Видно, что для апертуры  м энергетические потери не превышают 0.07 дБ.

Таблица 2. Оценки энергетических потерь  в зависимости от размера
прямоугольной апертуры антенны (угол рефракции   МГц).

,м	2	4	6	8	10
,дБ	-0.003	-0.011	-0.025	-0.044	-0.070

 

 На рис.4 приведены оценки дополнительного доплеровского смещения  несущей частоты  относительно доплеровского смещения в вакууме в зависимости от зенитного угла , вычисленные с использованием соотношения (6). Кривая 1 соответствует высоте спутника  км и  МГц, кривая 2 соответствует высоте  км и  ГГц. Видно, что максимальное значение  для  и  МГц не превышает 3.1 Гц, для  ГГц не превышает 1.6 Гц.

 

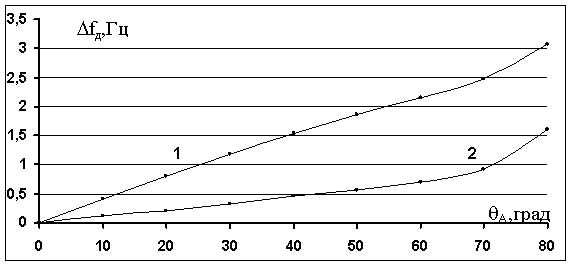
Рис.4. Зависимости дополнительного доплеровского смещения  несущей частоты  от зенитного угла :
кривая 1 - высота спутника  км,  МГц; кривая 2 - высота спутника  км,  ГГц.

 

В таблице 3 приведены оценочные значения различий времени распространения  в зависимости от зенитного угла  за счет влияния тропосферы и ионосферы, вычисленные с использованием соотношения (8) (в скобках приведены значения , вычисленные на основе приближения (9) в сочетании с корректирующими коэффициентами  для тропосферы (10) и для ионосферы (11)). Видно, что для  и высоты спутника  км максимальное значение  за счет тропосферы не превосходит 0.175 мкс.

 Таблица 3. Оценочные значения различий времени распространения  в зависимости от зенитного угла
за счет влияния тропосферы и ионосферы (в скобках даны значения , вычисленные на основе
приближения (8) в сочетании с корректирующими коэффициентами).

 

, град	Тропосфера	Ионосфера
	км, ,мкс	км, МГц ,мкс	км, ГГц ,мкс	км, МГц ,мкс
0	0.0176	0.181	0.0128	0.332
10	0.180(0.0179)	0.184(0.183)	0.0130(0.0129)	0.337
20	0.0187(0.0187)	0.192(0.191)	0.0137(0.0135)	0.351
30	0.0203(0.0203)	0.206(0.205)	0.0147(0.0145)	0.376
40	0.0230(0.0229)	0.230(0.228)	0.0164(0.0160)	0.417
50	0.0273(0.0273)	0.267(0.261)	0.0190(0.0185)	0.479
60	0.0350(0.0352)	0.326(0.312)	0.0231(0.223)	0.574
70	0.0510(0.0514)	0.419(0.387)	0.0298(0.0274)	0.716
80	0.175(0.101)	0.560(0.481)	0.0397(0.340)	0.910

 

Для ,  км и центральной частоты  МГц значение  за счет влияния ионосферы не превышает 0.56 мкс, при увеличении центральной частоты  различие времени распространения уменьшается и для  ГГц не превышает 0.04 мкс. Видно также, что для ,  км,  МГц значение  достигает 0.91 мкс. Вычисления показывают, что дальнейшее увеличение высоты спутника  практически не приводит к увеличению различий времени распространения .

Из таблицы 3 видно, что приближение (9) в сочетании с корректирующими коэффициентами является достаточно точным для зенитных углов .

Приведем результаты анализа оценивания различия путей распространения сигналов в атмосфере и в вакууме  и соответствующего различия времени распространения  с учетом искривления лучей из-за рефракции на основе соотношений (12), (13). Для корректного применения этих соотношений требуется достаточно точные значения угла рефракции . Вместе с тем соотношения (3), (4), используемые для оценивания , являются точными лишь при . Это является ограничивающим фактором применения методики оценки  и  на основе (12), (13) для произвольных значений . Задача аналитического построения пути распространения луча в атмосфере и точного вычисления углов рефракции рассмотрена в работах [15,20].

Результаты вычислений оценок  на основе соотношения (3) показали их недостаточную точность - при их использовании соответствующие производимые оценки  имели отрицательные значения, что не согласуется с моделью распространения луча.

Оценки , вычисляемые на основе соотношения (4), производили значения , что согласуется с моделью распространения луча в атмосфере. В этом случае значение  можно рассматривать в качестве оценки различия путей распространения сигналов в атмосфере и в вакууме. Вместе с тем, вычисленные значения оценок различий времени распространения  на основе соотношения (14) и оценок  при распространении сигналов через тропосферу и ионосферу для зенитных углов  практически совпали с соответствующими значениями , приведенными в таблице 3.

Заключение

Рассмотрено влияние атмосферы (тропосферы и ионосферы) на распространение сигналов «земная станция - спутник», которое заключается в рефракции лучей; в увеличении времени и пути распространения сигналов по отношению к распространению в вакууме; в дополнительном доплеровском смещении центральной и тактовой частот; в энергетических потерях при передаче и приеме сигналов за счет рефракции луча. Учет этих факторов требуется при разработке спутниковых систем связи и навигации.

Даны методики оценивания эффективностей приведенных факторов влияния атмосферы, рассмотрены модели тропосферы и ионосферы.

Приведены результаты оценивания характеристик рассматриваемых линий передачи с использованием описанных методик и моделей. В частности, показано, что основной вклад в рефракцию вносит тропосфера - углы рефракции достигают  для зенитных углов .

При вычислении характеристик ионосферных и тропосферных линий спутниковых систем связи возникают ошибки оценивания метрических расстояний и времени задержки. Это обусловлено отличием групповой скорости распространения радиоволн от скорости распространения в вакууме, а также искривлением луча относительно прямолинейного распространения. Аналитическое построение пути распространения луча в атмосфере и точное вычисление углов рефракции, ошибок оценивания метрических расстояний и времени задержки является темой перспективных исследований.

 

Литература

1. Спилкер Дж. Цифровая спутниковая связь. Пер. с англ. М.: Связь. 1979.

2. Спутниковая связь и вещание: справочник. Под ред. Кантора Л.Я. М.: Радио и связь. 1997.

3. Ли У.К. Техника подвижной связи. Пер. с англ. М.: Радио и связь. 1985.

4. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Перевод с англ. М.: Издательский дом “Вильямс”. 2003.

5. Назаров Л.Е., Головкин И.В. Последовательные турбо-коды с пониженной сложностью алгоритмов приема.// Радиотехника и электроника. 2010. том 55. №10. Стр. 1193-1199.

6. Долуханов М.П. Распространение радиоволн. М.: Гос. Издательство по вопросам связи и радио. 1960.

7. Грудинская Г.П. Распространение радиоволн. М.: Высшая школа. 1975.

8. Яковлев О.И., Якубов В.П., Урядов В.П., Павельев А.Г. Распространение радиоволн. М.: ЛЕНАНД. 2009.

9. Назаров Л.Е., Игошин Е.В., Зудилин А.С. Разработка и реализация сигнально-кодовой конструкции для высокоскоростного канала БПЛА-Земля.// Журнал радиоэлектроники [электронный журнал]. 2013. №7. URL: http://jre.cplire.ru/jre/jul13/1/text.pdf.

10. Назаров Л.Е., Игошин Е.В., Зудилин А.С., Щеглов М.А. Разработка, реализация и испытания сигнально-кодовых конструкций для высокоскоростной радиолинии связи с БПЛА. // Успехи современной радиоэлектроники. 2014. №8. Стр. 68-74.

11. Камнев В.Е., Черкасов В.В., Чагин Г.В., Спутниковые сети связи. М.: Военный Парад. 2010. 608 с.

12. ГЛОНАСС: принципы построения и функционирования. Изд.4-е. Под ред. А.И.Перова, В.Н.Харисова. М.:Радиотехника. 2010.

13. Справочник по радиолокации. Том 1. Основы радиолокации. / Под ред. М.Сколник. М.: Советское радио. 1974.

14. Бин Б.Р., Даттон Е.Дж. Радиометеорология . Л.: Гидрометиздат. 1971.

15. Дэвис К. Радиоволны в ионосфере. М.:Мир. 1973.

16. Hofinann-Wellenhof B., Lichtenegger H., Collins J. Global Positioning System. Theory and Practice. // Springer-Verlag. New York. 1994.

17. Bilitza D., McKinnell L.-A., Reinisch B., Fuller-Rowell T. The International Reference Ionosphere (IRI) today and in the future.// Journal of Geodesy. 2011. V. 85. P. 909-920.

18. Брюнелли Б. Е.,. Намгаладзе А. А. Физика ионосферы. М.: Наука, 1988.

19. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука. 1987.

20. Детков А.Н., Жеребцов С.И., Кобузев А.Н., Макаров И.А. Наведение радиолуча на цель с учетом рефракции в атмосфере Земли. // Журнал радиоэлектроники [электронный журнал]. 2013. №10. URL: http://jre.cplire.ru/jre/jul13/1/text.pdf.